【洛谷 P3367】【模板】并查集 题解(并查集+路径压缩)
【模板】并查集
题目描述
如题,现在有一个并查集,你需要完成合并和查询操作。
输入格式
第一行包含两个整数 N , M N,M N,M ,表示共有 N N N 个元素和 M M M 个操作。
接下来 M M M 行,每行包含三个整数 Z i , X i , Y i Z_i,X_i,Y_i Zi,Xi,Yi 。
当 Z i = 1 Z_i=1 Zi=1 时,将 X i X_i Xi 与 Y i Y_i Yi 所在的集合合并。
当 Z i = 2 Z_i=2 Zi=2 时,输出 X i X_i Xi 与 Y i Y_i Yi 是否在同一集合内,是的输出
Y ;否则输出 N 。
输出格式
对于每一个 Z i = 2 Z_i=2 Zi=2 的操作,都有一行输出,每行包含一个大写字母,为 Y 或者 N 。
样例 #1
样例输入 #1
4 7
2 1 2
1 1 2
2 1 2
1 3 4
2 1 4
1 2 3
2 1 4
样例输出 #1
N
Y
N
Y
提示
对于 30 % 30\% 30% 的数据, N ≤ 10 N \le 10 N≤10, M ≤ 20 M \le 20 M≤20。
对于 70 % 70\% 70% 的数据, N ≤ 100 N \le 100 N≤100, M ≤ 1 0 3 M \le 10^3 M≤103。
对于 100 % 100\% 100% 的数据, 1 ≤ N ≤ 1 0 4 1\le N \le 10^4 1≤N≤104, 1 ≤ M ≤ 2 × 1 0 5 1\le M \le 2\times 10^5 1≤M≤2×105, 1 ≤ X i , Y i ≤ N 1 \le X_i, Y_i \le N 1≤Xi,Yi≤N, Z i ∈ { 1 , 2 } Z_i \in \{ 1, 2 \} Zi∈{1,2}。
思路
首先,定义一个大小为 N N N的数组pre,用于记录每个元素的父节点。init函数用于初始化并查集,使得每个元素的父节点都是自己。
root函数用于查找元素 x x x的根节点,即在并查集中寻找 x x x所在集合的代表元素。这里采用路径压缩的方法,即在查找过程中,将 x x x到根节点的路径上的所有节点的父节点都直接设为根节点,从而优化后续查找效率。
merge函数用于合并两个集合,具体操作是找到两个元素的根节点,如果根节点不同,就将其中一个集合的根节点的父节点设置为另一个集合的根节点,从而实现两个集合的合并。
check函数用于检查两个元素是否在同一集合中,通过比较两个元素的根节点是否相同来判断。如果相同,输出"Y";如果不同,输出"N"。
在main函数中,首先读取元素的数量 n n n和操作的数量 m m m,然后进行初始化。接下来,根据输入的操作类型,进行合并或者检查操作。如果操作类型为1,执行merge函数合并两个集合;如果操作类型为2,执行check函数检查两个元素是否在同一集合中。
使用路径压缩优化后,代码运行用时大幅度缩短。但是路径压缩会破坏树形结构。
AC代码
#include <iostream>
#define AUTHOR "HEX9CF"
using namespace std;const int N = 1e5 + 7;int pre[N];void init(int x) {for (int i = 1; i <= x; i++) {pre[i] = i;}
}int root(int x) {int i = x;while (pre[i] != i) {i = pre[i];}return pre[x] = i;
}void merge(int x, int y) {x = root(x);y = root(y);if (x == y) {return;}pre[x] = y;
}void check(int x, int y) {x = root(x);y = root(y);if (x == y) {printf("Y\n");} else {printf("N\n");}
}int main() {int n, m;scanf("%d %d", &n, &m);init(n);while (m--) {int z, x, y;scanf("%d %d %d", &z, &x, &y);if (z == 1) {merge(x, y);} else {check(x, y);}}return 0;
}
相关文章:
)
【洛谷 P3367】【模板】并查集 题解(并查集+路径压缩)
【模板】并查集 题目描述 如题,现在有一个并查集,你需要完成合并和查询操作。 输入格式 第一行包含两个整数 N , M N,M N,M ,表示共有 N N N 个元素和 M M M 个操作。 接下来 M M M 行,每行包含三个整数 Z i , X i , Y i Z_i,X_i,Y…...
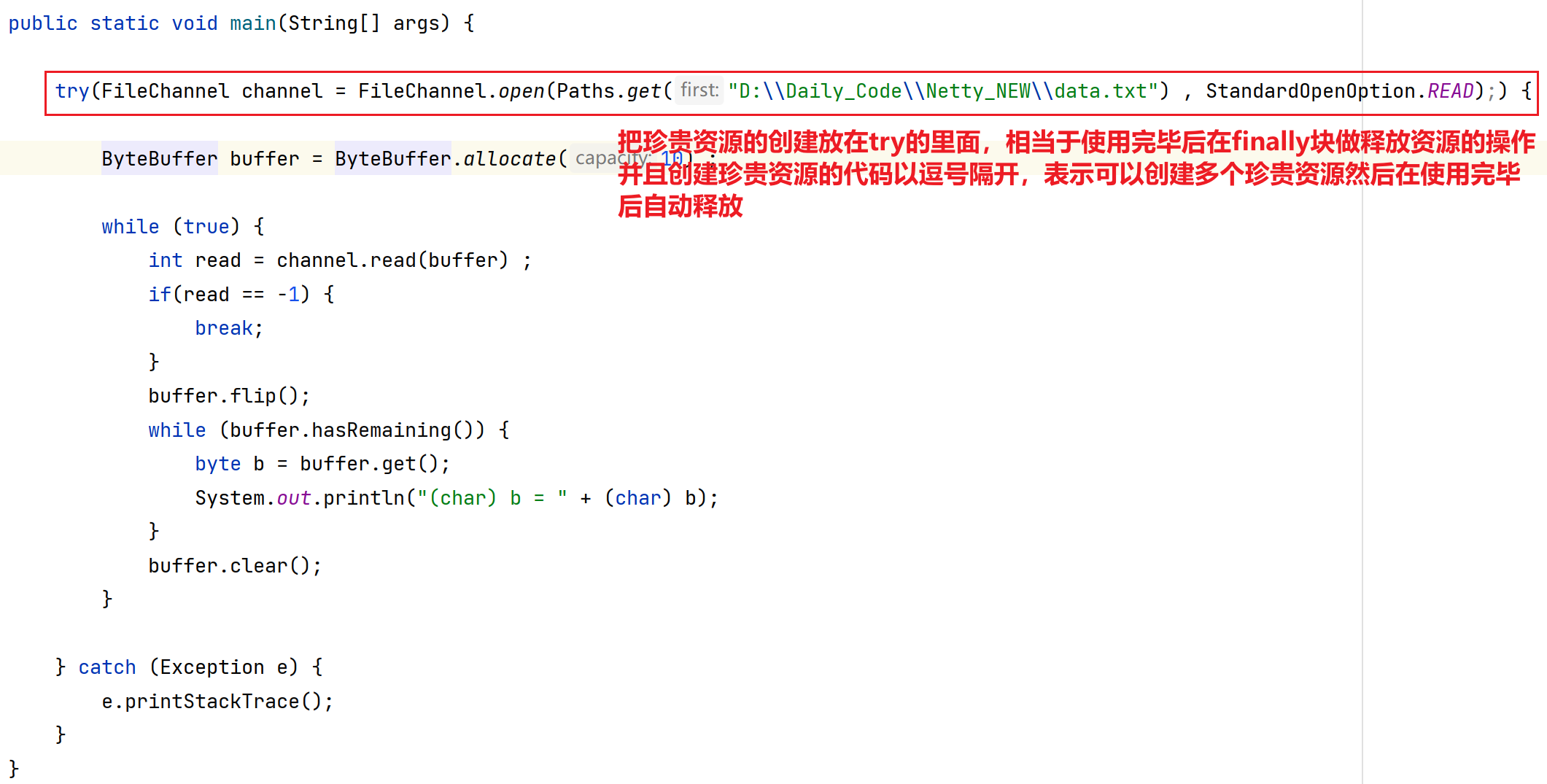
Netty应用(一) 之 NIO概念 基本编程
目录 第一章 概念引入 1.分布式概念引入 第二章 Netty基础 - NIO 1.引言 1.1 什么是Netty? 1.2 为什么要学习Netty? 2.NIO编程 2.1 传统网络通信中开发方式及问题(BIO) 2.1.1 多线程版网络编程 2.1.2 线程池版的网络编程…...
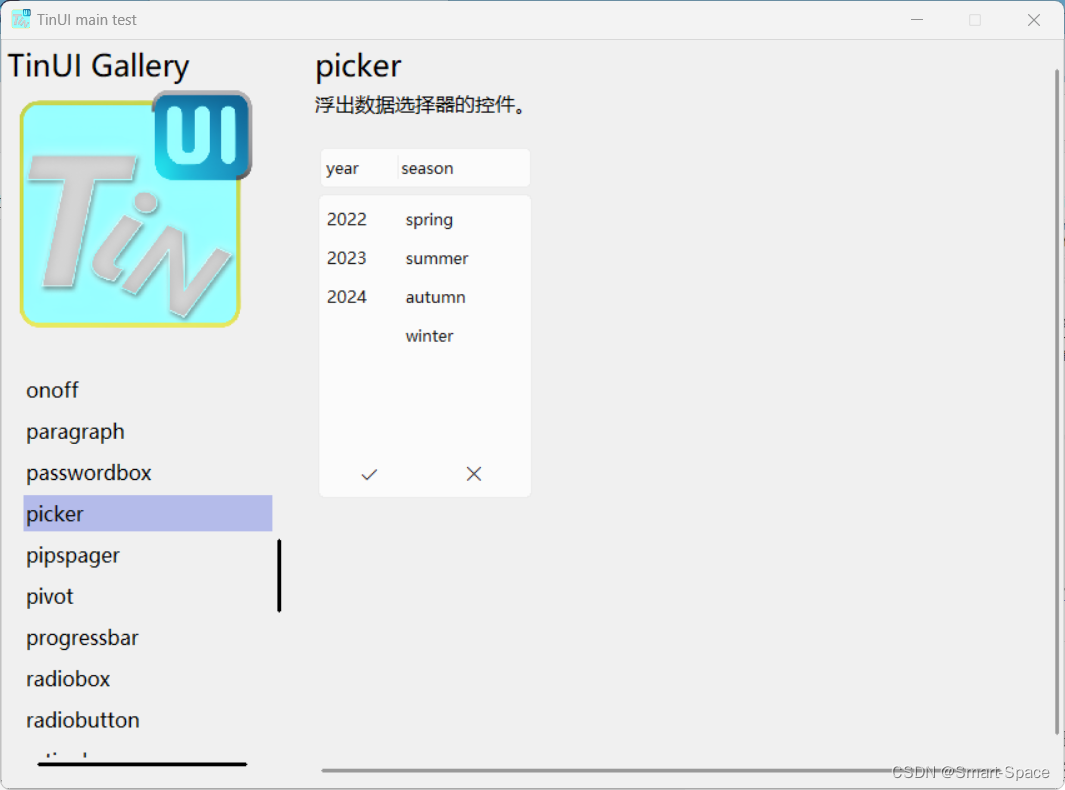
tkinter-TinUI-xml实战(10)展示画廊
tkinter-TinUI-xml实战(10)展示画廊 引言声明文件结构核心代码主界面统一展示控件控件展示界面单一展示已有展示多类展示 最终效果在这里插入图片描述  ………… 结语 引言…...
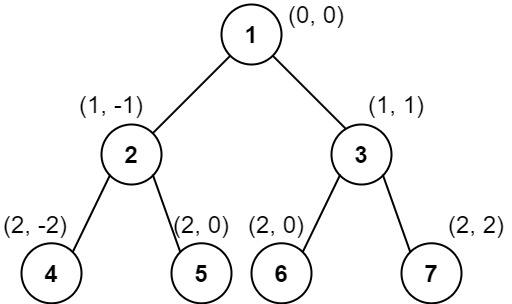
LeetCode二叉树的垂序遍历
题目描述 给你二叉树的根结点 root ,请你设计算法计算二叉树的 垂序遍历 序列。 对位于 (row, col) 的每个结点而言,其左右子结点分别位于 (row 1, col - 1) 和 (row 1, col 1) 。树的根结点位于 (0, 0) 。 二叉树的 垂序遍历 从最左边的列开始直到…...
 函数用法)
[linux c]linux do_div() 函数用法
linux do_div() 函数用法 do_div() 是一个 Linux 内核中的宏,用于执行 64 位整数的除法操作,并将结果存储在给定的变量中,同时将余数存储在另一个变量中。这个宏通常用于内核编程中,特别是在处理大整数和性能敏感的场合。 函数原…...

Python学习之路-爬虫提高:常见的反爬手段和解决思路
Python学习之路-爬虫提高:常见的反爬手段和解决思路 常见的反爬手段和解决思路 明确反反爬的主要思路 反反爬的主要思路就是:尽可能的去模拟浏览器,浏览器在如何操作,代码中就如何去实现。浏览器先请求了地址url1,保留了cookie…...

python_numpy库_ndarray的聚合操作、矩阵操作等
一、ndarray的聚合操作 1、求和np.sum() import numpy as np n np.arange(10) print(n) s np.sum(n) print(s) n np.random.randint(0,10,size(3,5)) print(n) s1 np.sum(n) print(s1) #全部数加起来 s2 np.sum(n,axis0) print(s2) #表示每一列的多行求和 …...
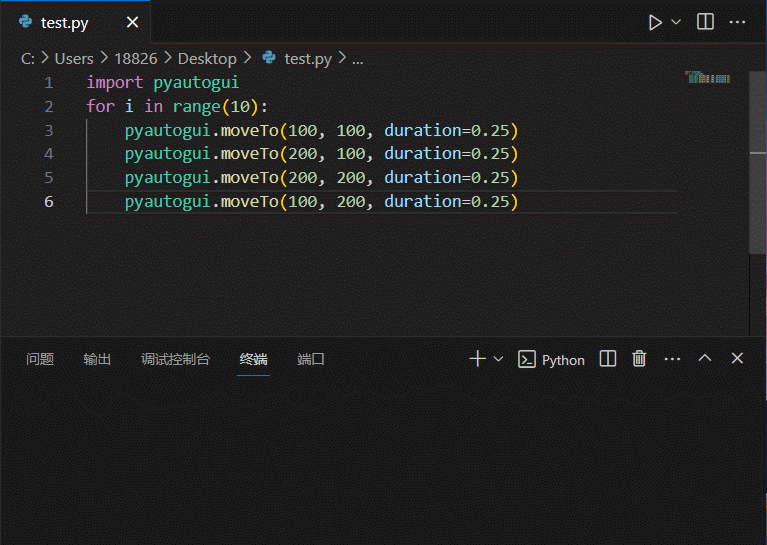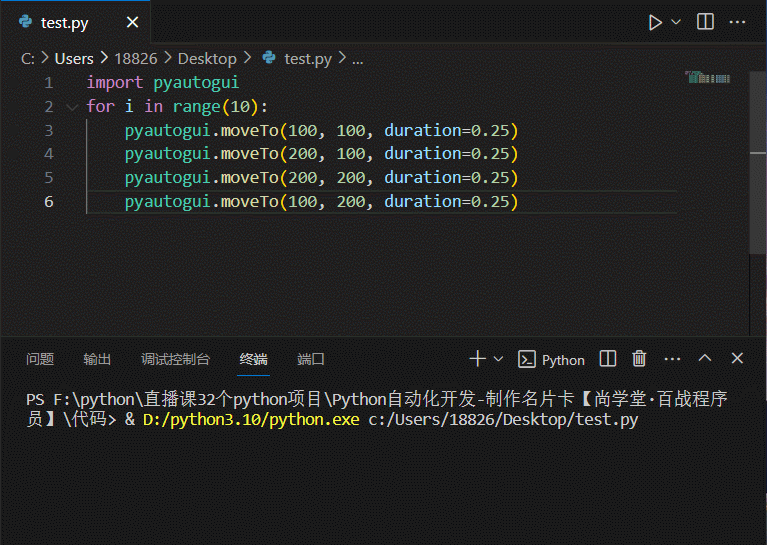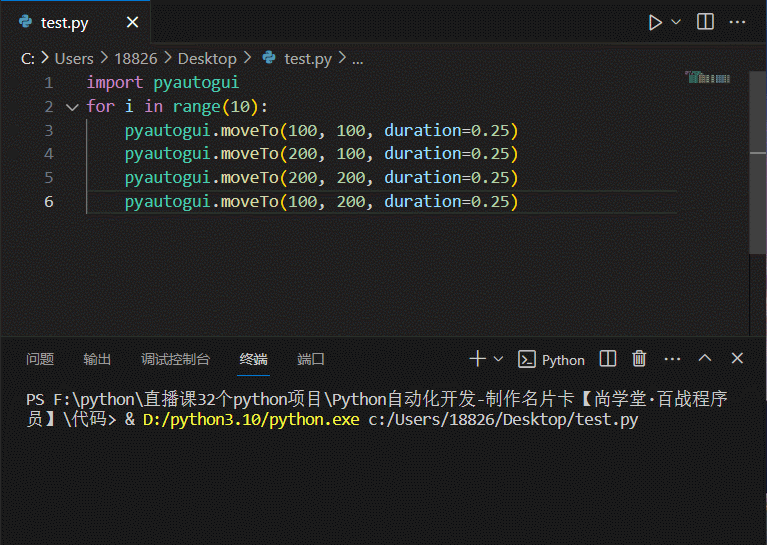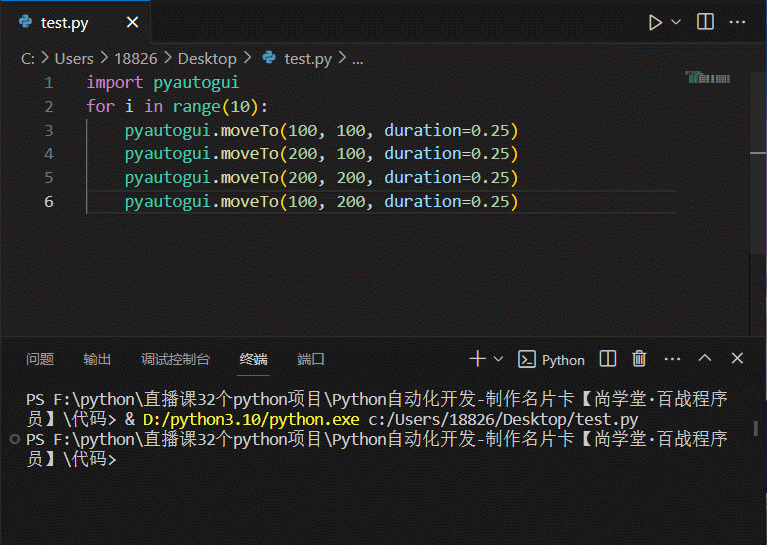
python-自动化篇-终极工具-用GUI自动控制键盘和鼠标-pyautogui
文章目录 用GUI自动控制键盘和鼠标pyautogui 模块鼠标屏幕位置——移动地图——pyautogui.size鼠标位置——自身定位——pyautogui.position()移动鼠标——pyautogui.moveTo拖动鼠标滚动鼠标 键盘按下键盘释放键盘 开始与结束通过注销关闭所有程序 用GUI自动控制键盘和鼠标 在…...
面试:大数据和深度学习之间的关系是什么?
大数据与深度学习之间存在着紧密的相互关系,它们在当今技术发展中相辅相成。 大数据的定义与特点:大数据指的是规模(数据量)、多样性(数据类型)和速度(数据生成及处理速度)都超出了传统数据处理软件和硬件能力范围的数据集。它具有四个主要特点,通常被称…...

航芯ACM32G103开发板评测 08 ADC Timer外设测试
航芯ACM32G103开发板评测 08 ADC Timer外设测试 1. 软硬件平台 ACM32G103 Board开发板MDK-ARM Keil 2. 定时器Timer 在一般的MCU芯片中,定时器这个外设资源是非常重要的,一般可以分为SysTick定时器(系统滴答定时器)、常规定时…...

【Linux学习】生产者-消费者模型
目录 22.1 什么是生产者-消费者模型 22.2 为什么要用生产者-消费者模型? 22.3 生产者-消费者模型的特点 22.4 BlockingQueue实现生产者-消费者模型 22.4.1 实现阻塞队列BlockQueue 1) 添加一个容器来存放数据 2)加入判断Blocking Queue情况的成员函数 3)实现push和pop方法 4)完…...
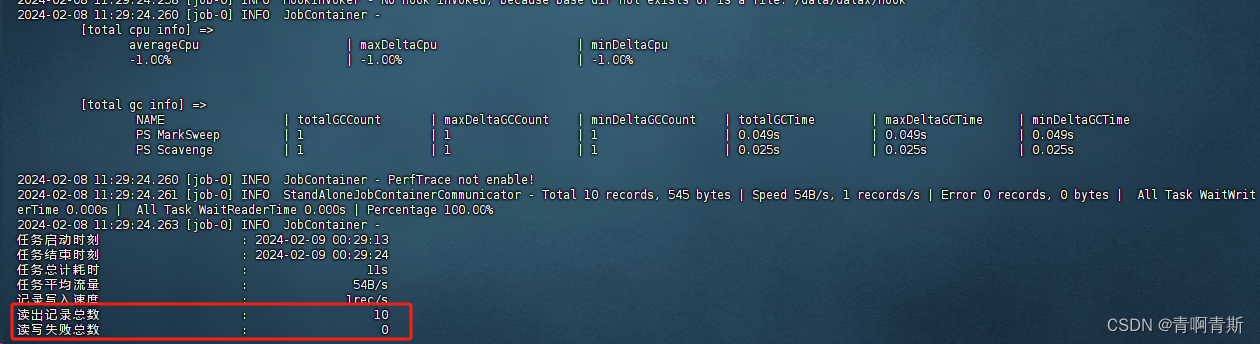
三、案例 - MySQL数据迁移至ClickHouse
MySQL数据迁移至ClickHouse 一、生成测试数据表和数据1.在MySQL创建数据表和数据2.在ClickHouse创建数据表 二、生成模板文件1.模板文件内容2.模板文件参数详解2.1 全局设置2.2 数据读取(Reader)2.3 数据写入(Writer)2.4 性能设置…...

[WinForm开源]概率计算器 - Genshin Impact(V1.0)
创作目的:为方便旅行者估算自己拥有的纠缠之缘能否达到自己的目的,作者使用C#开发了一款小型软件供旅行者参考使用。 创作说明:此软件所涉及到的一切概率与规则完全按照游戏《原神》(V4.4.0)内公示的概率与规则(包括保底机制&…...
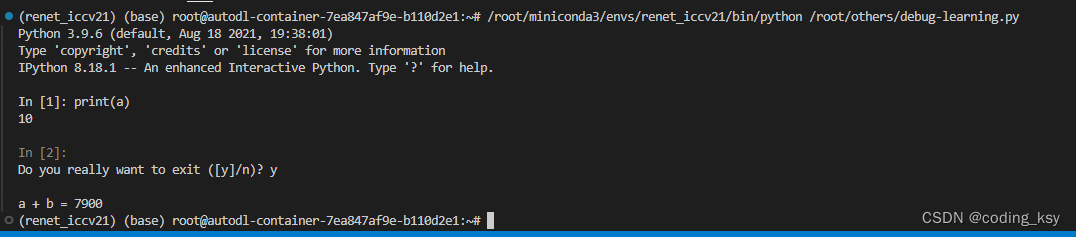
vscode 代码调试from IPython import embed
一、讲解 这种代码调试方法非常的好用。 from IPython import embed上面的代码片段是用于Python中嵌入一个交互式IPython shell的方法。这可以在任何Python脚本或程序中实现,允许在执行到该点时暂停程序,并提供一个交互式环境,以便于检查、…...
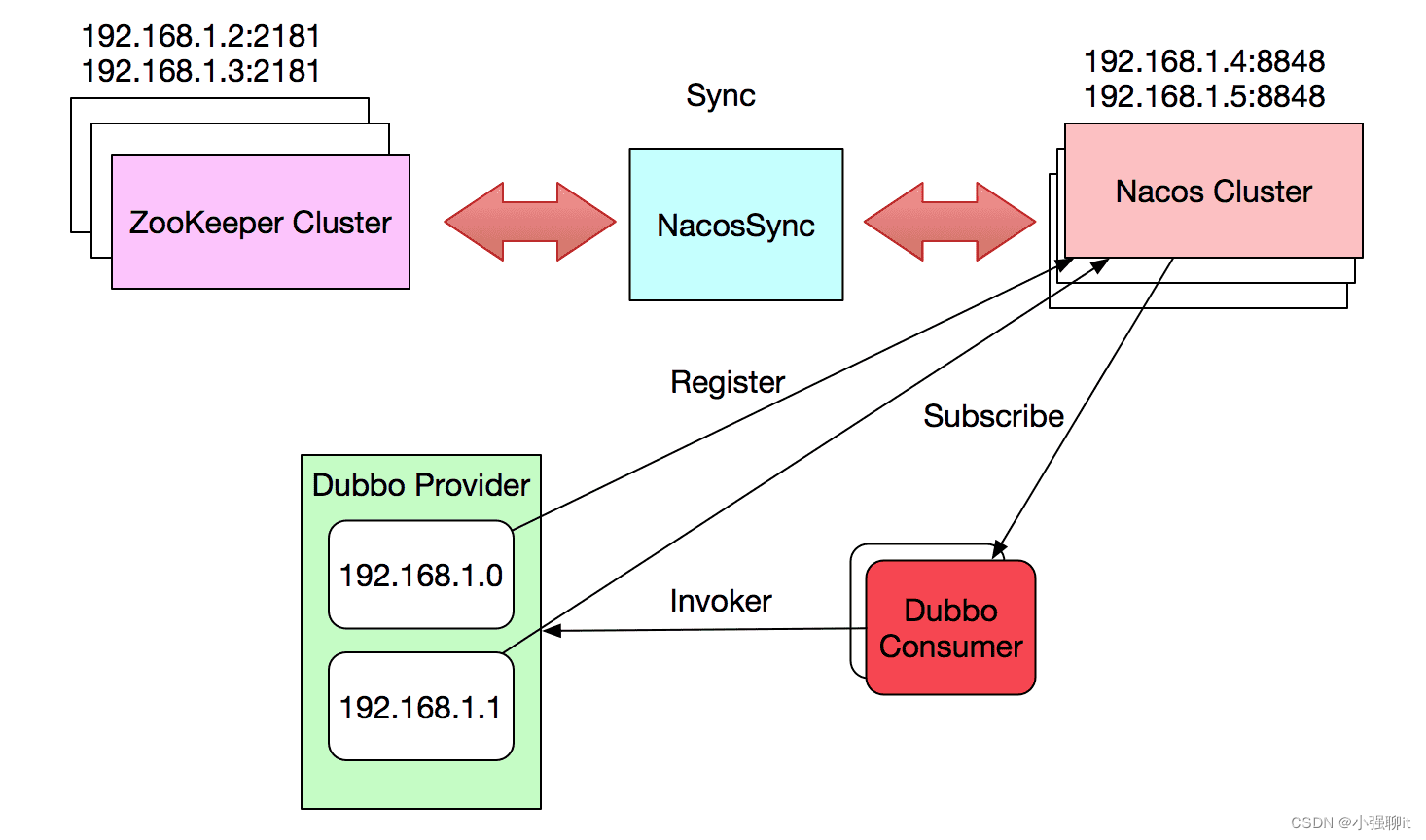
双活工作关于nacos注册中心的数据迁移
最近在做一个双活的项目,在纠结一个注册中心是在双活机房都准备一个,那主机房的数据如果传过去呢,查了一些资料,最终在官网查到了一个NacosSync 的组件,主要用来做数据传输的,并且支持在线替换注册中心的&a…...
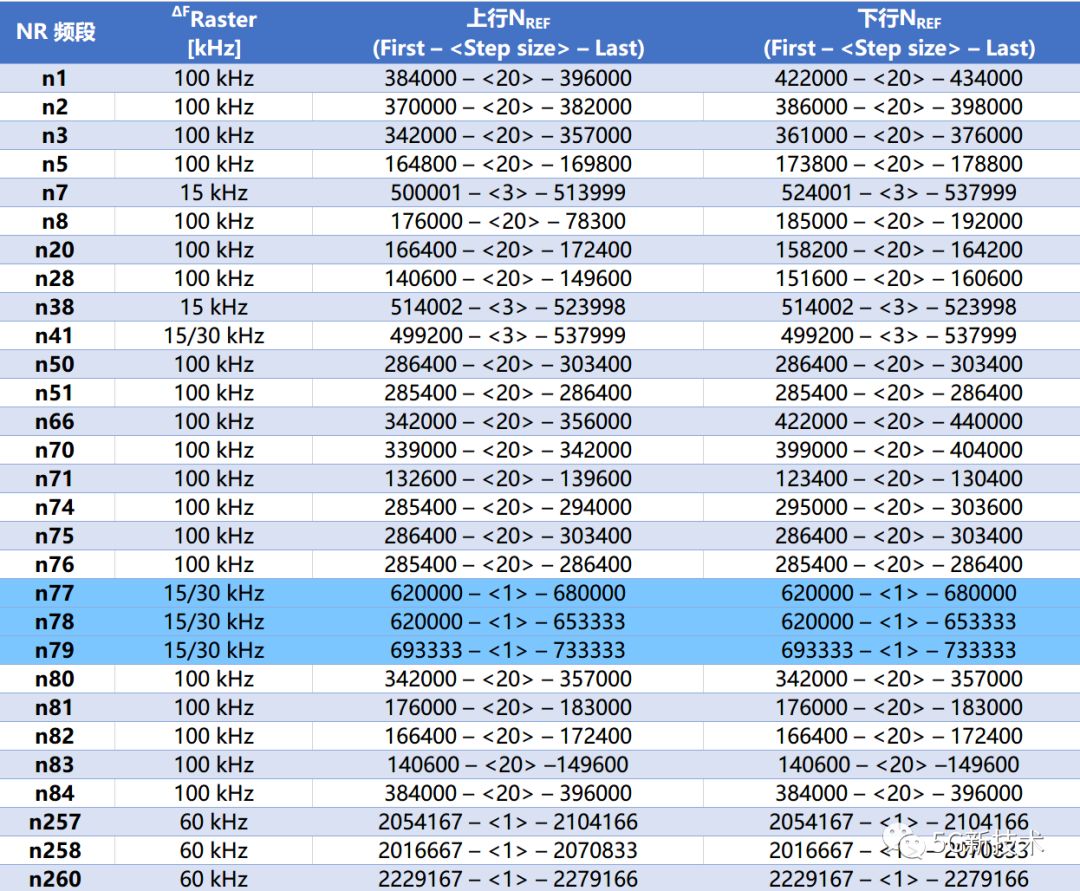
5G NR 信道号计算
一、5G NR的频段 增加带宽是增加容量和传输速率最直接的方法,目前5G最大带宽将会达到400MHz,考虑到目前频率占用情况,5G将不得不使用高频进行通信。 3GPP协议定义了从Sub6G(FR1)到毫米波(FR2)的5G目标频谱。 其中FR1是5G的核心频段࿰…...
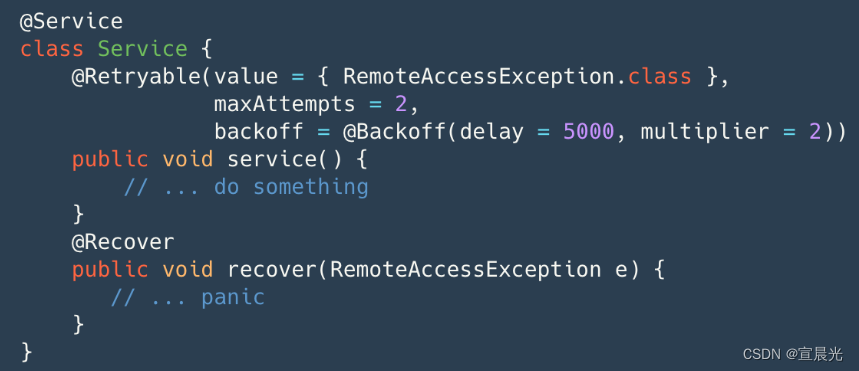
01-Spring实现重试和降级机制
主要用于在模块调用中,出现失败、异常情况下,仍需要进行重复调用。并且在最终调用失败时,可以采用降级措施,返回一般结果。 1、重试机制 我们采用spring 提供的retry 插件,其原理采用aop机制,所以需要额外…...
docker部署showdoc
目录 安装 1.拉取镜像 2.创建容器 使用 1.选择语言 2.默认账户/密码:showdoc/123456编辑 3.登陆 4.首页 安装 1.拉取镜像 docker pull star7th/showdoc 2.创建容器 mkdir -p /opt/showdoc/html docker run -d --name showdoc --userroot --privilegedtrue -p 1005…...

2.14作业
1.请编程实现二维数组的杨辉三角。 2.请编程实现二维数组计算每一行的和以及列和。 3.请编程实现二维数组计算第二大值。 4.请使用非函数方法实现系统函数strcat,strcmp,strcpy,strlen. strcat: strcmp: strcpy: strlen:...
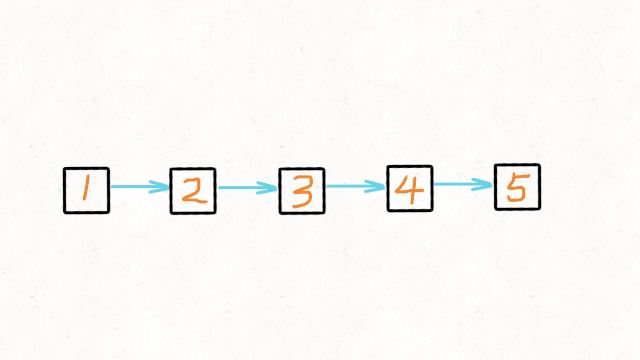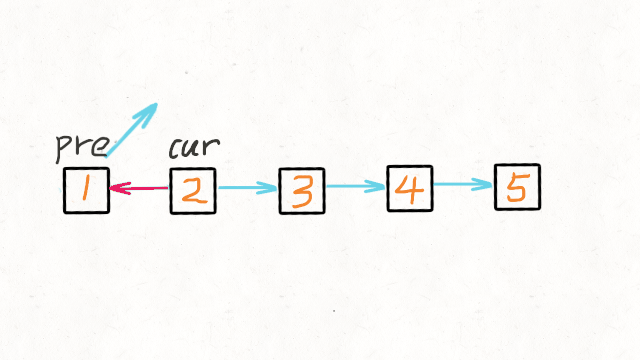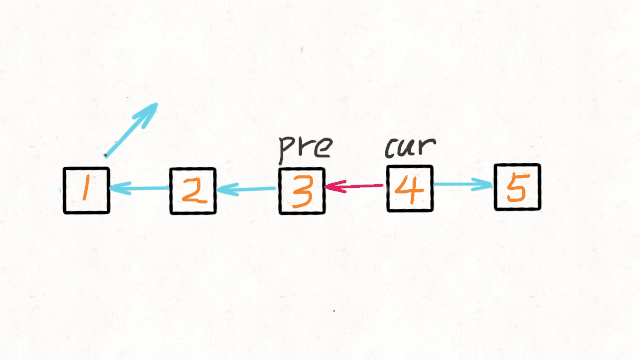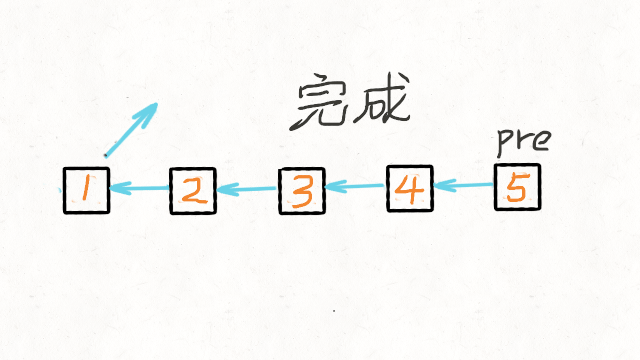
01.数据结构篇-链表
1.找出两个链表的交点 160. Intersection of Two Linked Lists (Easy) Leetcode / 力扣 例如以下示例中 A 和 B 两个链表相交于 c1: A: a1 → a2↘c1 → c2 → c3↗ B: b1 → b2 → b3 但是不会出现以下相交的情况,因为每个节点只有一个…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
