[linux c]linux do_div() 函数用法
linux do_div() 函数用法
do_div() 是一个 Linux 内核中的宏,用于执行 64 位整数的除法操作,并将结果存储在给定的变量中,同时将余数存储在另一个变量中。这个宏通常用于内核编程中,特别是在处理大整数和性能敏感的场合。
函数原型如下:
#define do_div(n, base) ({ \ unsigned int __base = (base); \ unsigned int __rem; \ __rem = ((u64)(n)) % __base; \ (n) = ((u64)(n)) / __base; \ __rem; \
})参数说明:
n:要进行除法的 64 位整数。
base:除数,一个 32 位整数。
返回值:
宏的返回值是 n 除以 base 的余数。
使用 do_div() 的好处是,它可以在一次操作中同时得到商和余数,而且不需要额外的临时变量。
示例用法:
#include <linux/kernel.h> int main(void) { u64 num = 1234567890123456ULL; u32 base = 1000; u32 remainder; remainder = do_div(num, base); printk("商: %llu\n", num); printk("余数: %u\n", remainder); return 0;
}
在这个示例中,num 被 1000 除,商存储在 num 中,余数存储在 remainder 中。输出将是:
商: 1234567890123
余数: 456
请注意,do_div() 宏在 Linux 内核中使用,因此在非内核代码中使用可能不是最佳选择。如果你正在编写用户空间程序,建议使用标准的 C 语言除法操作符 / 和取模操作符 %。
相关文章:
 函数用法)
[linux c]linux do_div() 函数用法
linux do_div() 函数用法 do_div() 是一个 Linux 内核中的宏,用于执行 64 位整数的除法操作,并将结果存储在给定的变量中,同时将余数存储在另一个变量中。这个宏通常用于内核编程中,特别是在处理大整数和性能敏感的场合。 函数原…...

Python学习之路-爬虫提高:常见的反爬手段和解决思路
Python学习之路-爬虫提高:常见的反爬手段和解决思路 常见的反爬手段和解决思路 明确反反爬的主要思路 反反爬的主要思路就是:尽可能的去模拟浏览器,浏览器在如何操作,代码中就如何去实现。浏览器先请求了地址url1,保留了cookie…...

python_numpy库_ndarray的聚合操作、矩阵操作等
一、ndarray的聚合操作 1、求和np.sum() import numpy as np n np.arange(10) print(n) s np.sum(n) print(s) n np.random.randint(0,10,size(3,5)) print(n) s1 np.sum(n) print(s1) #全部数加起来 s2 np.sum(n,axis0) print(s2) #表示每一列的多行求和 …...
python-自动化篇-终极工具-用GUI自动控制键盘和鼠标-pyautogui
文章目录 用GUI自动控制键盘和鼠标pyautogui 模块鼠标屏幕位置——移动地图——pyautogui.size鼠标位置——自身定位——pyautogui.position()移动鼠标——pyautogui.moveTo拖动鼠标滚动鼠标 键盘按下键盘释放键盘 开始与结束通过注销关闭所有程序 用GUI自动控制键盘和鼠标 在…...
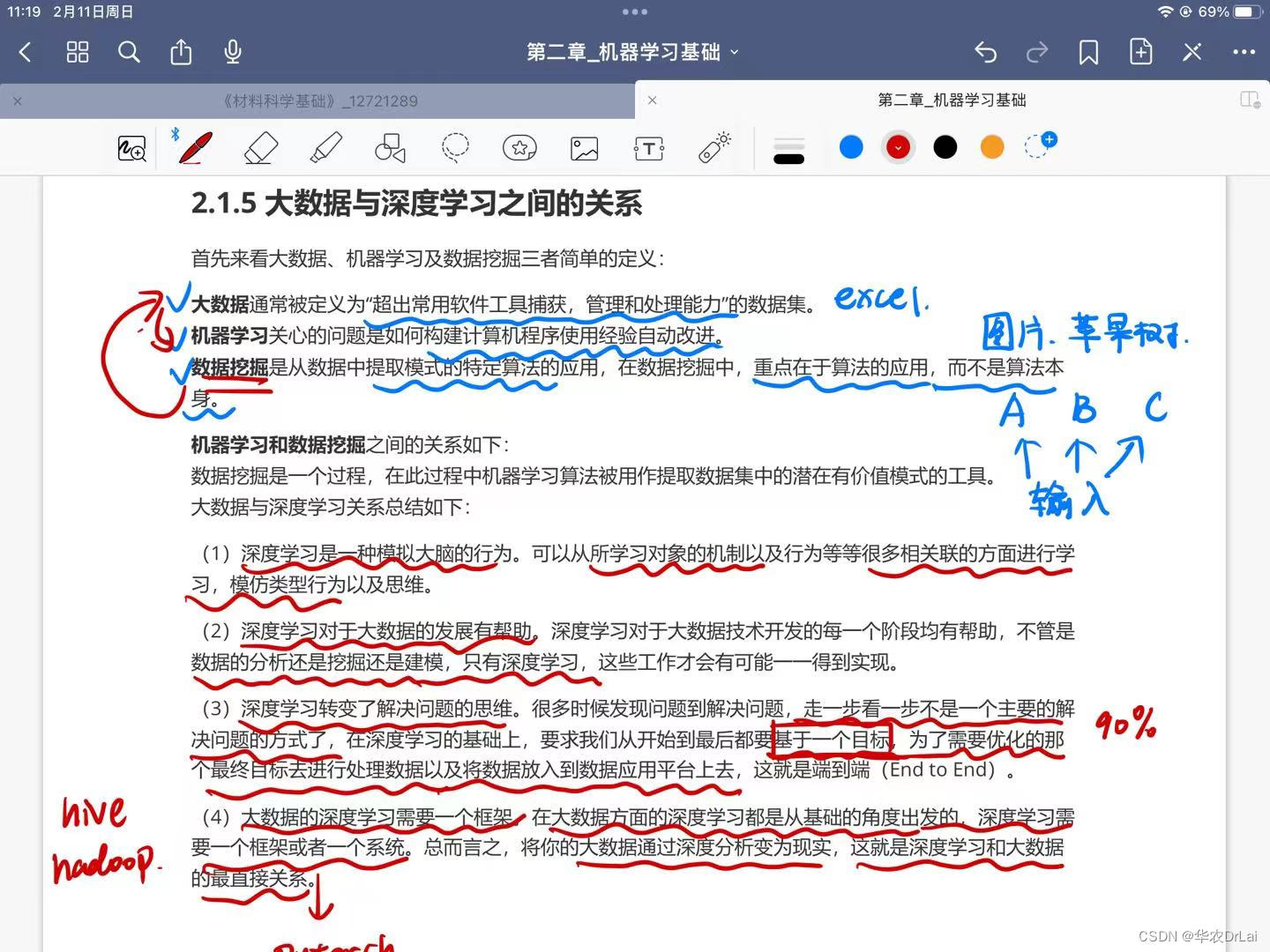
面试:大数据和深度学习之间的关系是什么?
大数据与深度学习之间存在着紧密的相互关系,它们在当今技术发展中相辅相成。 大数据的定义与特点:大数据指的是规模(数据量)、多样性(数据类型)和速度(数据生成及处理速度)都超出了传统数据处理软件和硬件能力范围的数据集。它具有四个主要特点,通常被称…...

航芯ACM32G103开发板评测 08 ADC Timer外设测试
航芯ACM32G103开发板评测 08 ADC Timer外设测试 1. 软硬件平台 ACM32G103 Board开发板MDK-ARM Keil 2. 定时器Timer 在一般的MCU芯片中,定时器这个外设资源是非常重要的,一般可以分为SysTick定时器(系统滴答定时器)、常规定时…...

【Linux学习】生产者-消费者模型
目录 22.1 什么是生产者-消费者模型 22.2 为什么要用生产者-消费者模型? 22.3 生产者-消费者模型的特点 22.4 BlockingQueue实现生产者-消费者模型 22.4.1 实现阻塞队列BlockQueue 1) 添加一个容器来存放数据 2)加入判断Blocking Queue情况的成员函数 3)实现push和pop方法 4)完…...
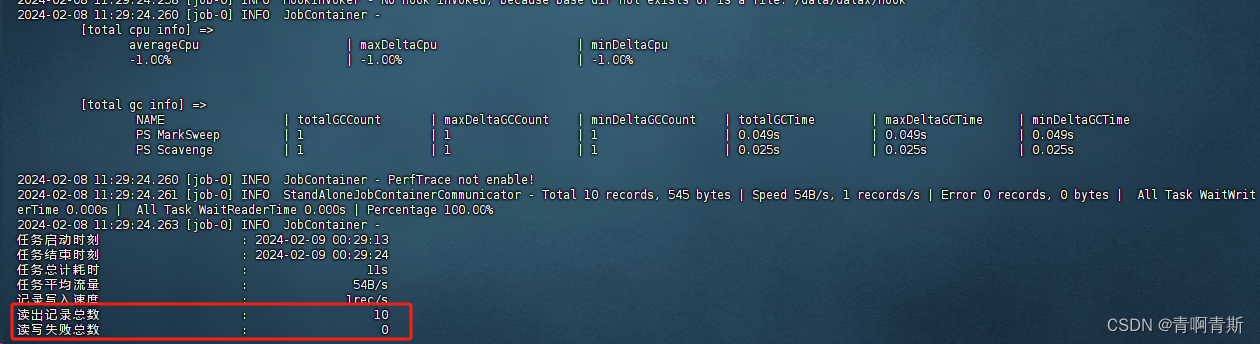
三、案例 - MySQL数据迁移至ClickHouse
MySQL数据迁移至ClickHouse 一、生成测试数据表和数据1.在MySQL创建数据表和数据2.在ClickHouse创建数据表 二、生成模板文件1.模板文件内容2.模板文件参数详解2.1 全局设置2.2 数据读取(Reader)2.3 数据写入(Writer)2.4 性能设置…...

[WinForm开源]概率计算器 - Genshin Impact(V1.0)
创作目的:为方便旅行者估算自己拥有的纠缠之缘能否达到自己的目的,作者使用C#开发了一款小型软件供旅行者参考使用。 创作说明:此软件所涉及到的一切概率与规则完全按照游戏《原神》(V4.4.0)内公示的概率与规则(包括保底机制&…...
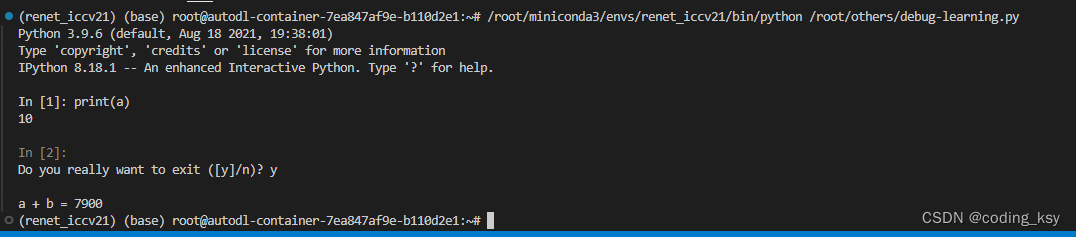
vscode 代码调试from IPython import embed
一、讲解 这种代码调试方法非常的好用。 from IPython import embed上面的代码片段是用于Python中嵌入一个交互式IPython shell的方法。这可以在任何Python脚本或程序中实现,允许在执行到该点时暂停程序,并提供一个交互式环境,以便于检查、…...
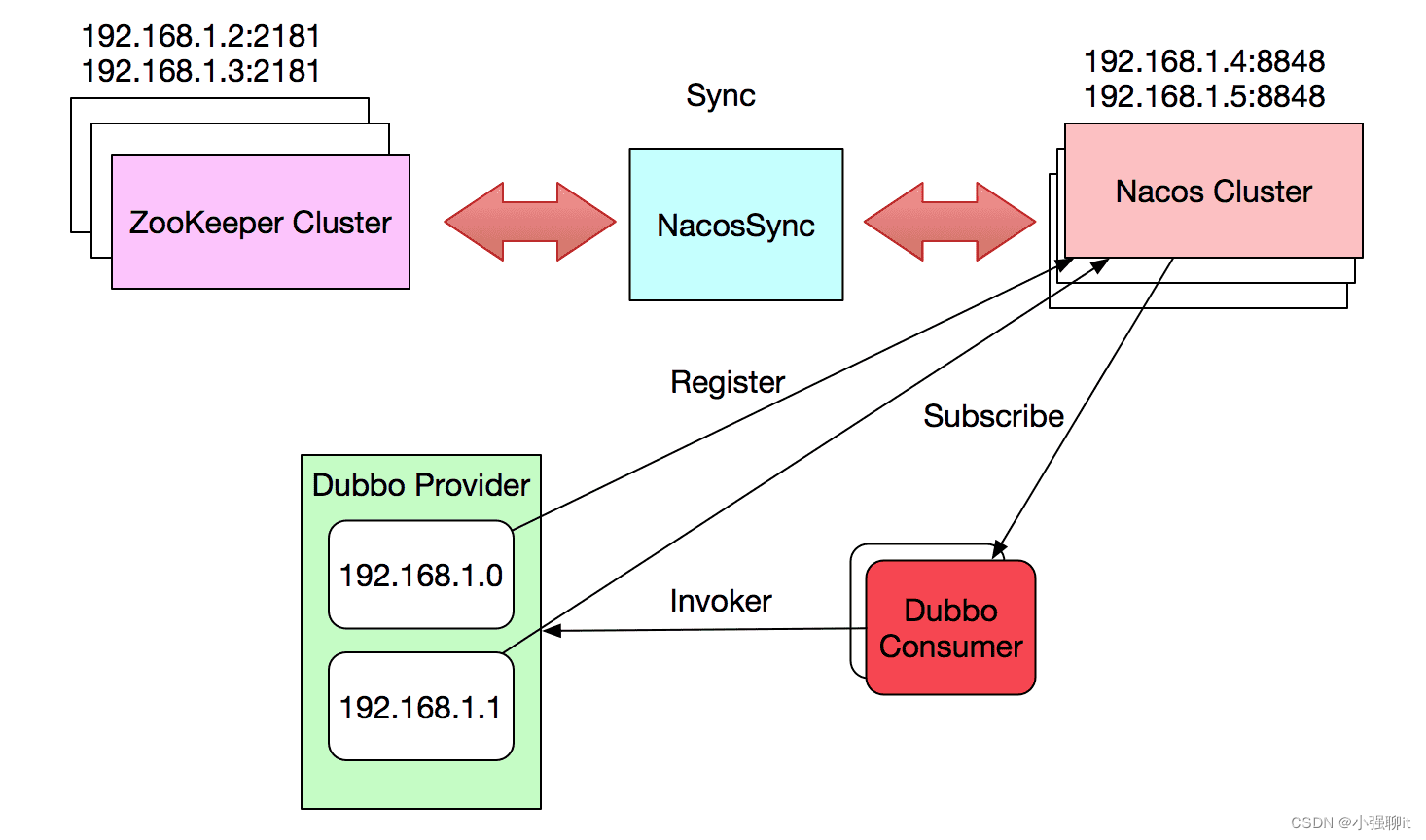
双活工作关于nacos注册中心的数据迁移
最近在做一个双活的项目,在纠结一个注册中心是在双活机房都准备一个,那主机房的数据如果传过去呢,查了一些资料,最终在官网查到了一个NacosSync 的组件,主要用来做数据传输的,并且支持在线替换注册中心的&a…...
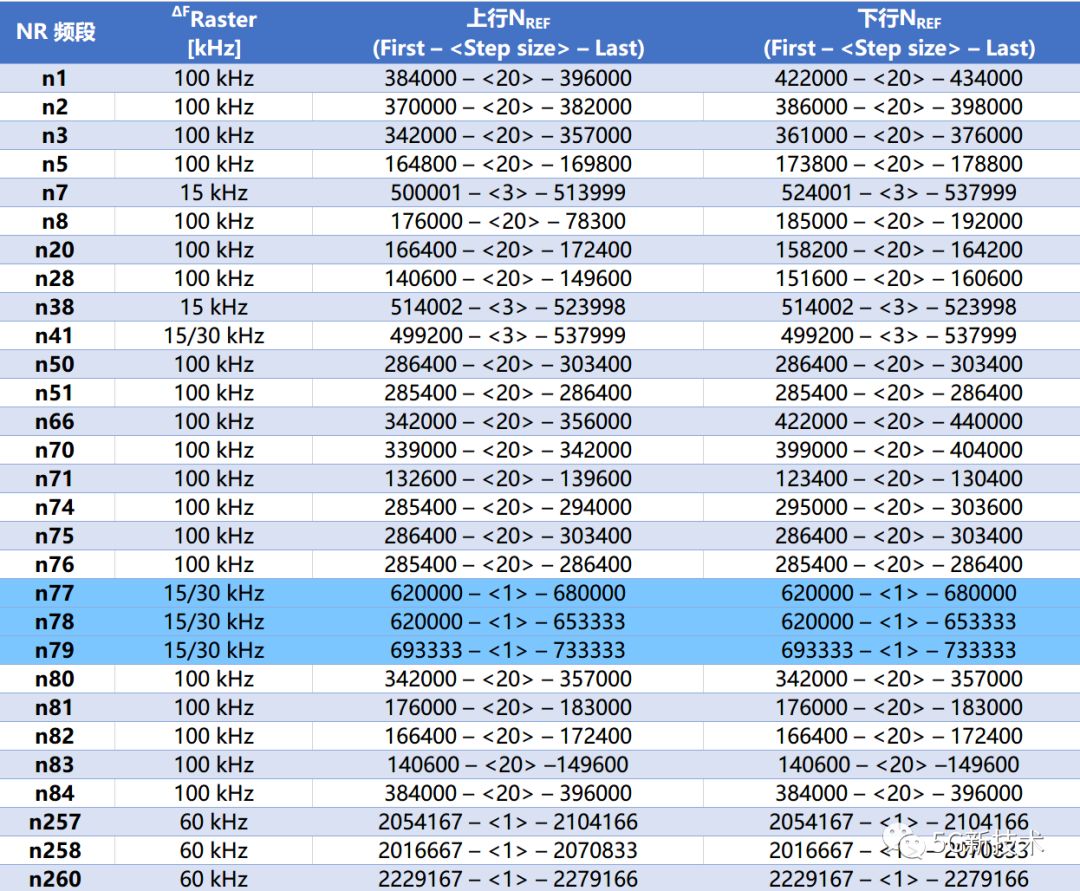
5G NR 信道号计算
一、5G NR的频段 增加带宽是增加容量和传输速率最直接的方法,目前5G最大带宽将会达到400MHz,考虑到目前频率占用情况,5G将不得不使用高频进行通信。 3GPP协议定义了从Sub6G(FR1)到毫米波(FR2)的5G目标频谱。 其中FR1是5G的核心频段࿰…...
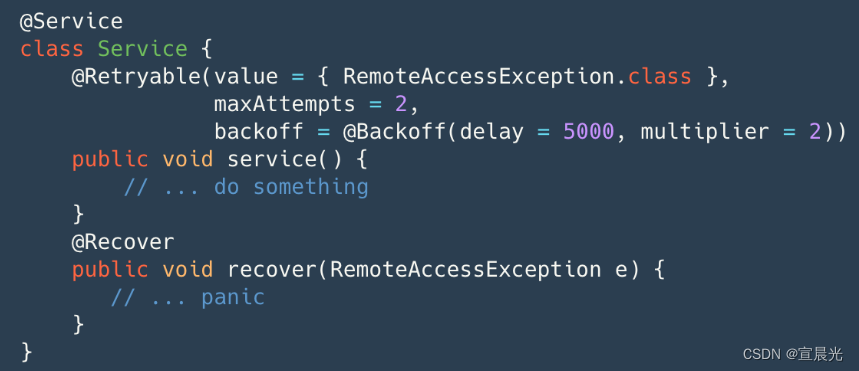
01-Spring实现重试和降级机制
主要用于在模块调用中,出现失败、异常情况下,仍需要进行重复调用。并且在最终调用失败时,可以采用降级措施,返回一般结果。 1、重试机制 我们采用spring 提供的retry 插件,其原理采用aop机制,所以需要额外…...
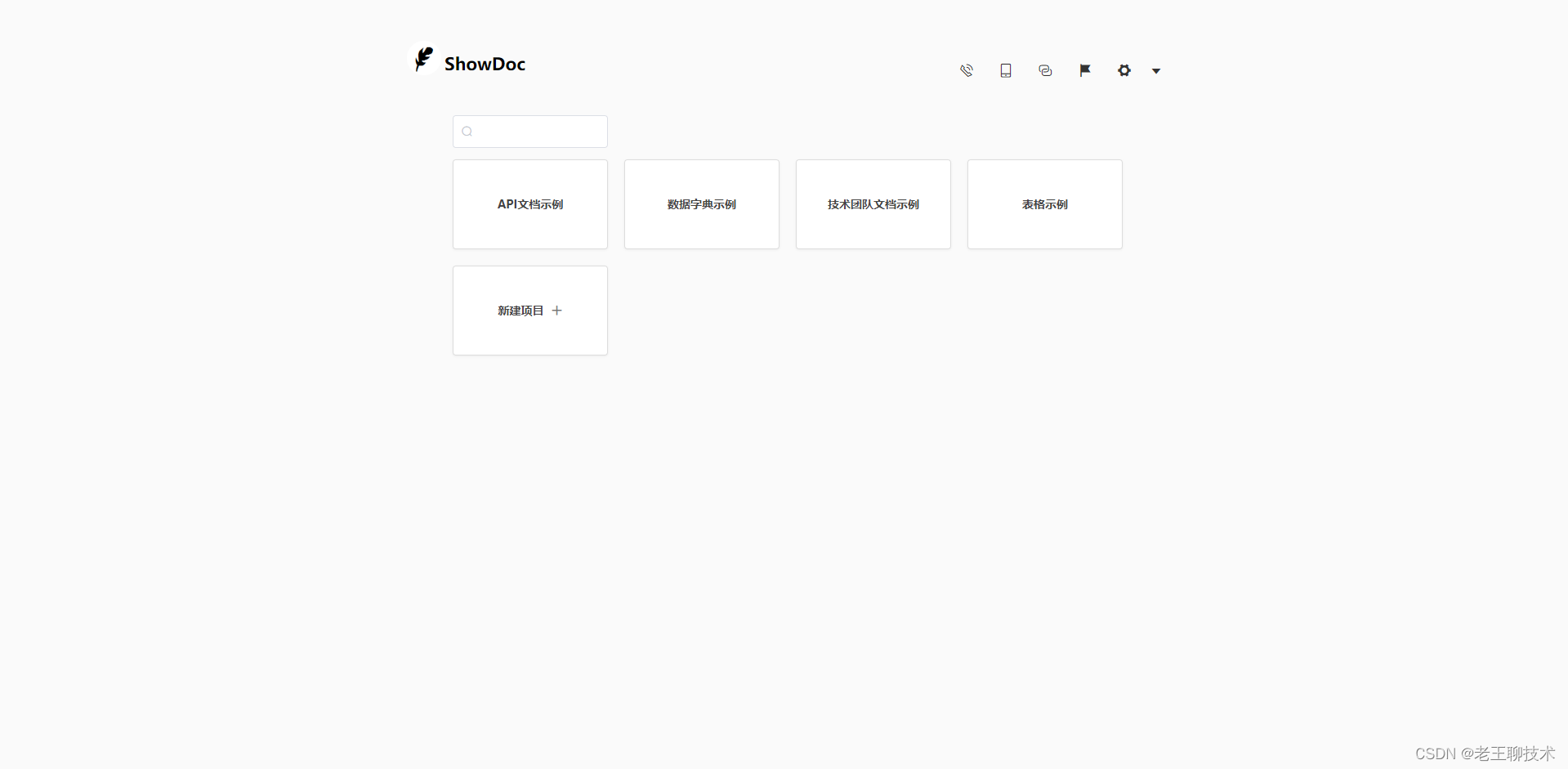
docker部署showdoc
目录 安装 1.拉取镜像 2.创建容器 使用 1.选择语言 2.默认账户/密码:showdoc/123456编辑 3.登陆 4.首页 安装 1.拉取镜像 docker pull star7th/showdoc 2.创建容器 mkdir -p /opt/showdoc/html docker run -d --name showdoc --userroot --privilegedtrue -p 1005…...

2.14作业
1.请编程实现二维数组的杨辉三角。 2.请编程实现二维数组计算每一行的和以及列和。 3.请编程实现二维数组计算第二大值。 4.请使用非函数方法实现系统函数strcat,strcmp,strcpy,strlen. strcat: strcmp: strcpy: strlen:...
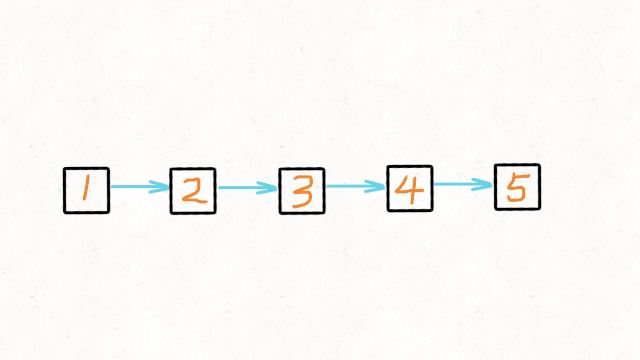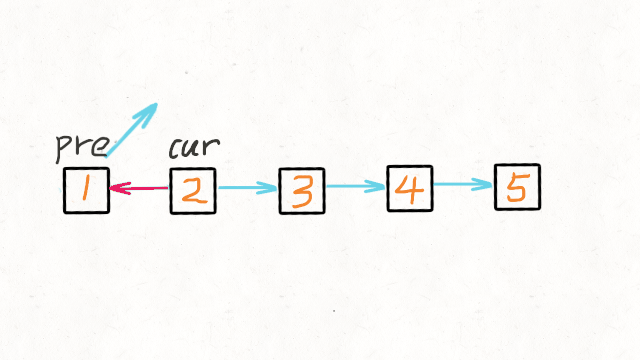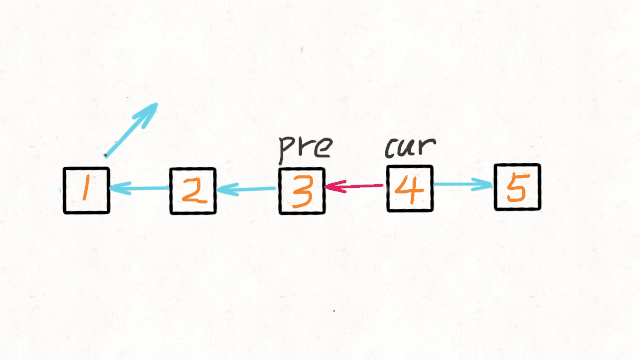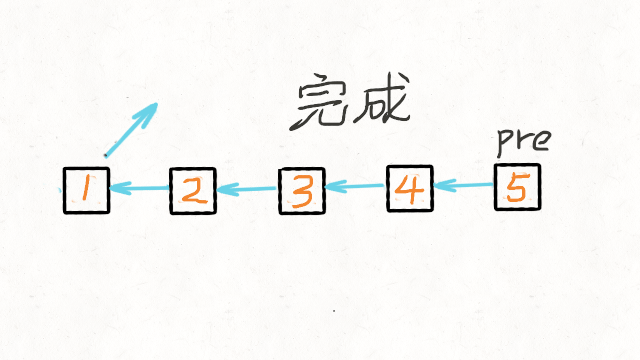
01.数据结构篇-链表
1.找出两个链表的交点 160. Intersection of Two Linked Lists (Easy) Leetcode / 力扣 例如以下示例中 A 和 B 两个链表相交于 c1: A: a1 → a2↘c1 → c2 → c3↗ B: b1 → b2 → b3 但是不会出现以下相交的情况,因为每个节点只有一个…...

揭秘产品迭代计划制定:从0到1打造完美迭代策略
产品迭代计划是产品团队确保他们能够交付满足客户需求的产品以及实现其业务目标的重要工具。开发一个成功的产品迭代计划需要仔细考虑产品的目标、客户需求、市场趋势和可用资源。以下是帮助您创建产品迭代计划的一些步骤:建立产品目标、收集客户反馈、分析市场趋势…...
Python进阶--下载想要的格言(基于格言网的Python爬虫程序)
注:由于上篇帖子(Python进阶--爬取下载人生格言(基于格言网的Python3爬虫)-CSDN博客)篇幅长度的限制,此篇帖子对上篇做一个拓展延伸。 目录 一、爬取格言网中想要内容的url 1、找到想要的内容 2、抓包分析,找到想…...
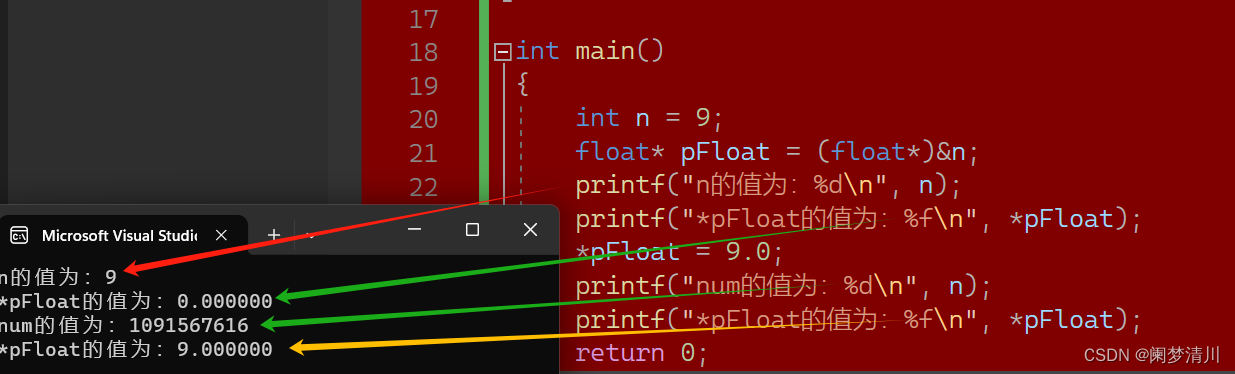
C语言--------数据在内存中的存储
1.整数在内存中的存储 整数在内存是以补码的形式存在的; 整型家族包括char,int ,long long,short类型; 因为char类型是以ASCII值形式存在,所以也是整形家族; 这四种都包括signed,unsigned两种,即有符号和无符号&am…...

【Java】零基础蓝桥杯算法学习——线性动态规划(一维dp)
线性dp——一维动态规划 1、考虑最后一步可以由哪些状态得到,推出转移方程 2、考虑当前状态与哪些参数有关系,定义几维数组来表示当前状态 3、计算时间复杂度,判断是否需要进行优化。 一维动态规划例题:最大上升子序列问题 Java参…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...
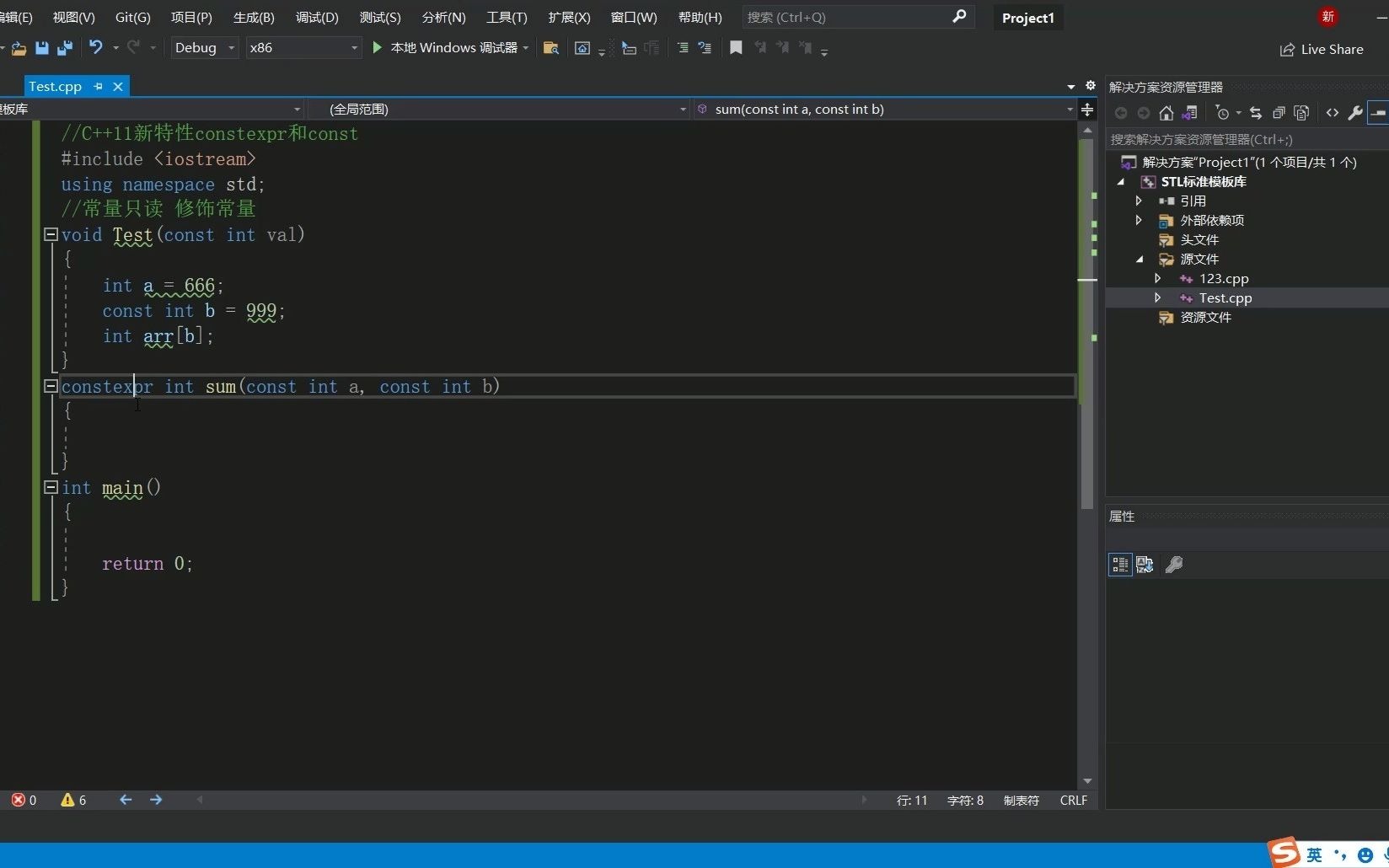
C++11 constexpr和字面类型:从入门到精通
文章目录 引言一、constexpr的基本概念与使用1.1 constexpr的定义与作用1.2 constexpr变量1.3 constexpr函数1.4 constexpr在类构造函数中的应用1.5 constexpr的优势 二、字面类型的基本概念与使用2.1 字面类型的定义与作用2.2 字面类型的应用场景2.2.1 常量定义2.2.2 模板参数…...
