机器学习2---逻辑回归(基础准备)
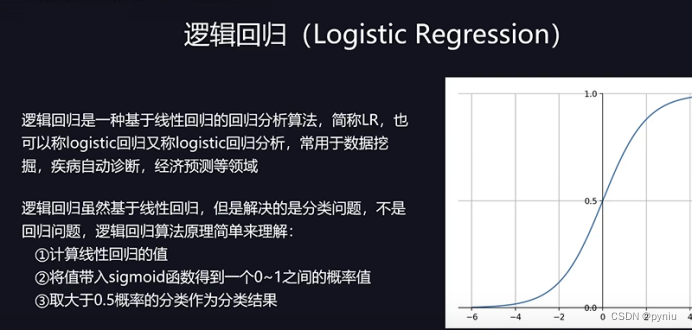


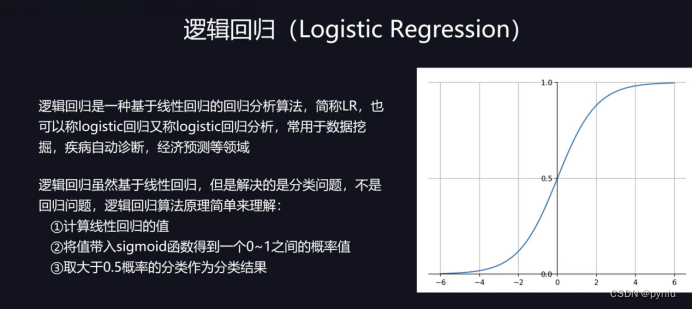
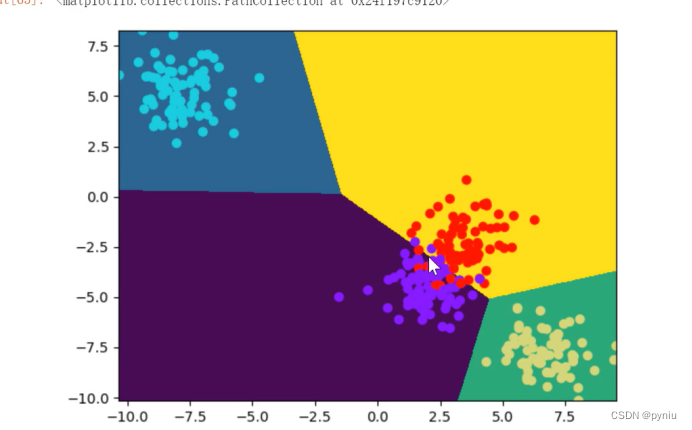
逻辑回归是基于线性回归是直线分的也可以做多分类
## 数学基础
import numpy as np
np.pi
# 三角函数
np.sin()
np.cos()
np.tan()
# 指数
y=3**x
# 对数
np.log10(10)
np.log2(2)
np.e
np.log(np.e) #ln(e)# 对数运算
# log(AB) = log(A) + logB
np.log(3*4)==np.log(3)+np.log(4)
# logA² = 2 * logA
np.log(3**4)==4*np.log(3)导数(Derivative),也叫导函数值。又名微商,是微积分中的重要基础概念。当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f'(x0)或df(x0)/dx。导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。然而,可导的函数一定连续;不连续的函数一定不可导。对于可导的函数f(x),x↦f'(x)也是一个函数,称作f(x)的导函数(简称导数)
矩阵: 在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合**方阵**: 行数、列数相等的矩阵阶: 方阵的行数或列数
import numpy as np
n=np.array([[1,2,9],[2,3,4]])
n
#### 矩阵求逆
# np.linalg: linear algebra 线性代数
# 求逆
np.linalg.inv(n)
# 行列式的值
np.linalg.det(n)
np.round(np.linalg.det(n)) #np.round()是NumPy库中的一个函数,用于对数组或单个数值进行四舍五入
**单位矩阵**在矩阵的乘法中,有一种矩阵起着特殊的作用,如同数的乘法中的1,这种矩阵被称为单位矩阵。它是个方阵,从左上角到右下角的对角线(称为主对角线)上的元素均为1。除此以外全都为0。根据单位矩阵的特点,任何矩阵与单位矩阵相乘都等于本身
矩阵积np.dot(n2, n)单位矩阵符合交换律: 任何矩阵与单位矩阵相乘都等于本身I是单位矩阵I.A = A.I = A
n1 = np.array([[1, 2, 3], [2, 3, 4]])
n2 = np.array([[1, 2, 3], [2, 3, 4], [3, 4, 5]])
display(n1,n2)
np.dot(n1,n2)
# 求n的逆
n_inv=np.linalg.inv(n)
n_inv
#### 矩阵的秩 (了解)定义: 在m * n矩阵A中, 最高阶非零子式的阶数,称为矩阵A的秩, 记作R(A)或r(A)linalg: linear algebra 线性代数
**满秩矩阵(non-singular matrix)**: 设A是n阶矩阵, 若r(A) = n, 则称A为满秩矩阵。但满秩不局限于n阶矩阵。若矩阵秩等于行数,称为行满秩;若矩阵秩等于列数,称为列满秩。既是行满秩又是列满秩则为n阶矩阵即n阶方阵。如果是方阵,行满秩矩阵与列满秩矩阵是等价的。满秩有行满秩和列满秩,既是行满秩又是列满秩的话就一定是是方阵
**奇异矩阵** 是线性代数的概念,就是该矩阵的秩不是满秩。首先,看这个矩阵是不是方阵(即行数和列数相等的矩阵。若行数和列数不相等,那就谈不上奇异矩阵和非奇异矩阵)
相关文章:

机器学习2---逻辑回归(基础准备)
逻辑回归是基于线性回归是直线分的也可以做多分类 ## 数学基础 import numpy as np np.pi # 三角函数 np.sin() np.cos() np.tan() # 指数 y3**x # 对数 np.log10(10) np.log2(2) np.e np.log(np.e) #ln(e)# 对数运算 # log(AB) log(A) logB np.log(3*4)np.log(3)np.log(4) #…...

JVM体系
JVM是一种虚拟的计算机,它模拟了一个完整的硬件系统,并运行在一个完全隔离的环境中。这意味着JVM可以看作是一个在操作系统之上的计算机系统,与VMware、Virtual Box等虚拟机类似。JVM的设计目标是提供一个安全、可靠、高效且跨平台的运行环境…...

.NET命令行(CLI)常用命令
本文用于记录了.NET软件开发全生命周期各阶段常用的一些CLI命令,用于开发速查。 .NET命令行(CLI)常用命令 项目创建(1)查看本机SDK(2)查看本机可以使用的.NET版本(3)生成…...
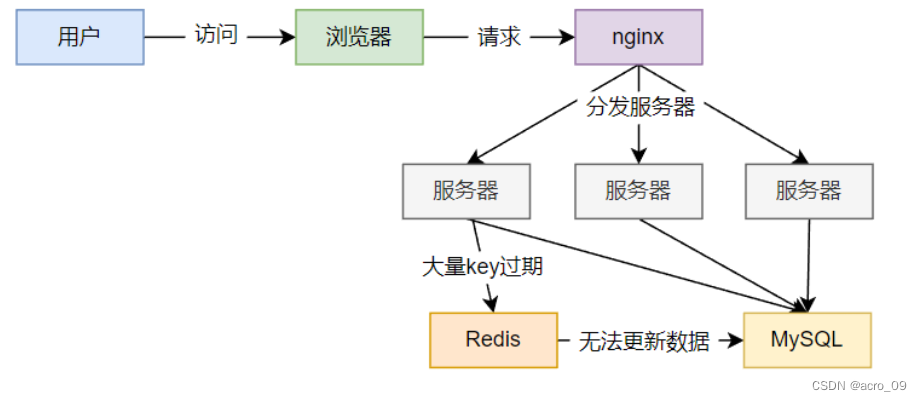
六、Redis之数据持久化及高频面试题
6.1 数据持久化 官网文档地址:https://redis.io/docs/manual/persistence/ Redis提供了主要提供了 2 种不同形式的持久化方式: RDB(Redis数据库):RDB 持久性以指定的时间间隔执行数据集的时间点快照。AOF࿰…...
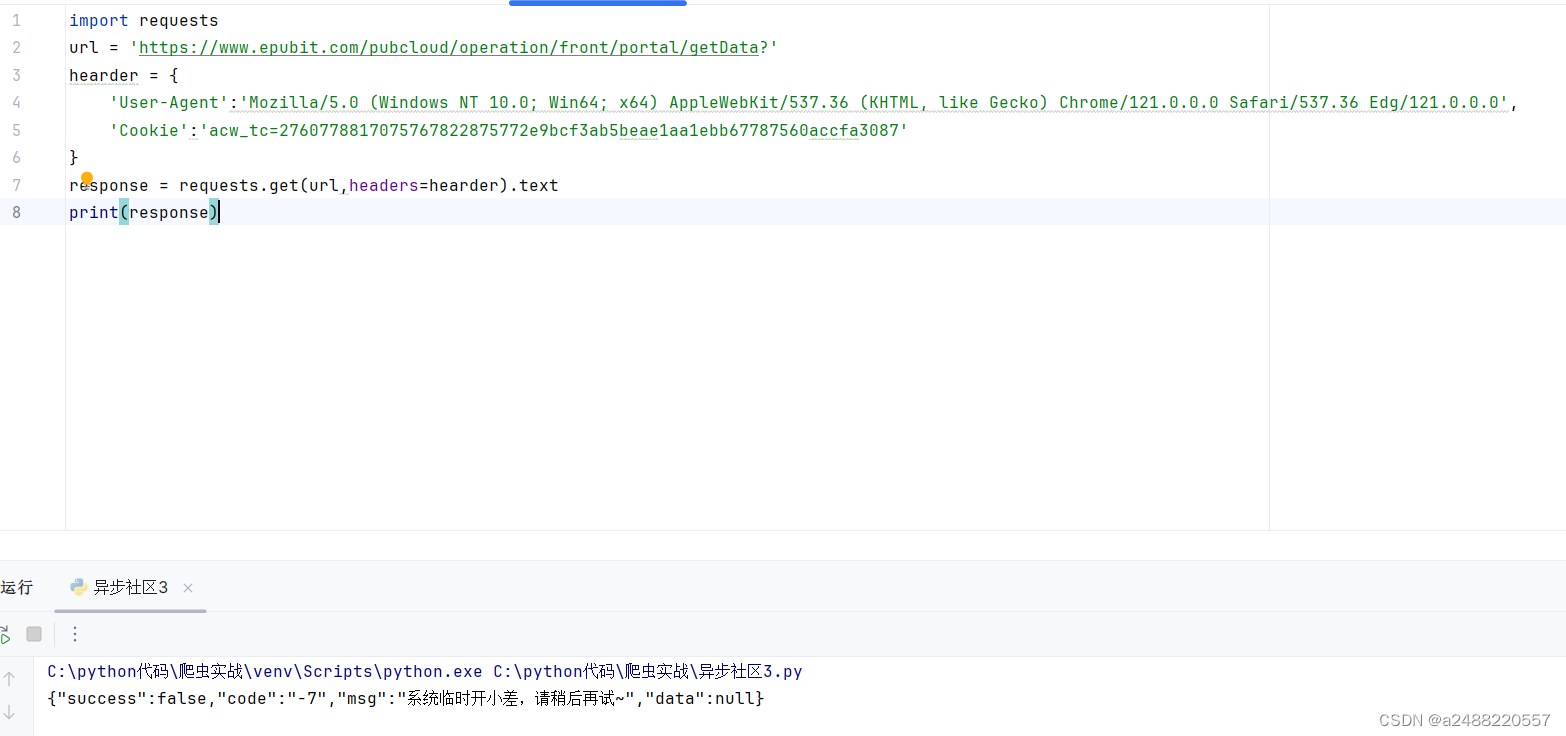
爬虫——ajax和selenuim总结
为什么要写这个博客呢,这个代码前面其实都有,就是结束了。明天搞个qq登录,这个就结束了。 当然也会更新小说爬取,和百度翻译,百度小姐姐的爬取,的对比爬取。总结嘛!!!加…...

【Python】单元测试unittest框架
note 使用unittest框架进行单元测试是Python标准库的一部分,提供了编写测试用例、测试套件以及运行测试的能力。测试用例是继承自unittest.TestCase的类。在这个类中,你可以定义一系列的方法来测试不同的行为。每个测试方法都应该以test开头。 文章目录…...

(三十七)大数据实战——Solr服务的部署安装
前言 Solr是一个基于Apache Lucene的开源搜索平台,它提供了强大的全文搜索、分布式搜索和数据分析功能。Solr 可以用于构建高性能的搜索应用程序,支持从海量数据中快速检索和分析信息。Solr 使用倒排索引和先进的搜索算法,可实现快速而准确的…...
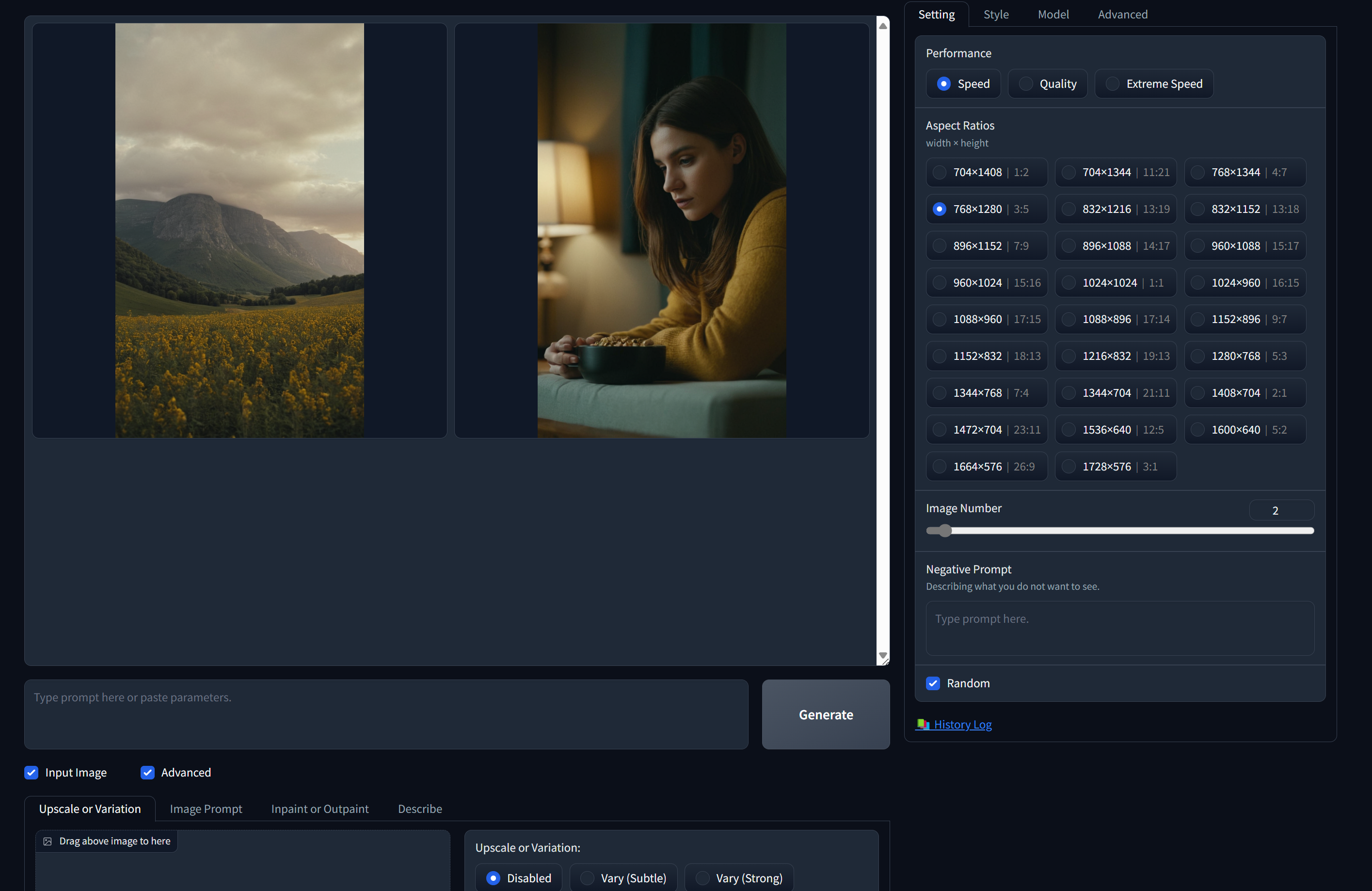
在Ubuntu22.04上部署FoooCUS2.1
Fooocus 是一款基于 Gradio的图像生成软件,Fooocus 是对 Stable Diffusion 和 Midjourney 设计的重新思考: 1、从 Stable Diffusion 学习,该软件是离线的、开源的和免费的。 2、从 Midjourney 中学到,不需要手动调整,…...
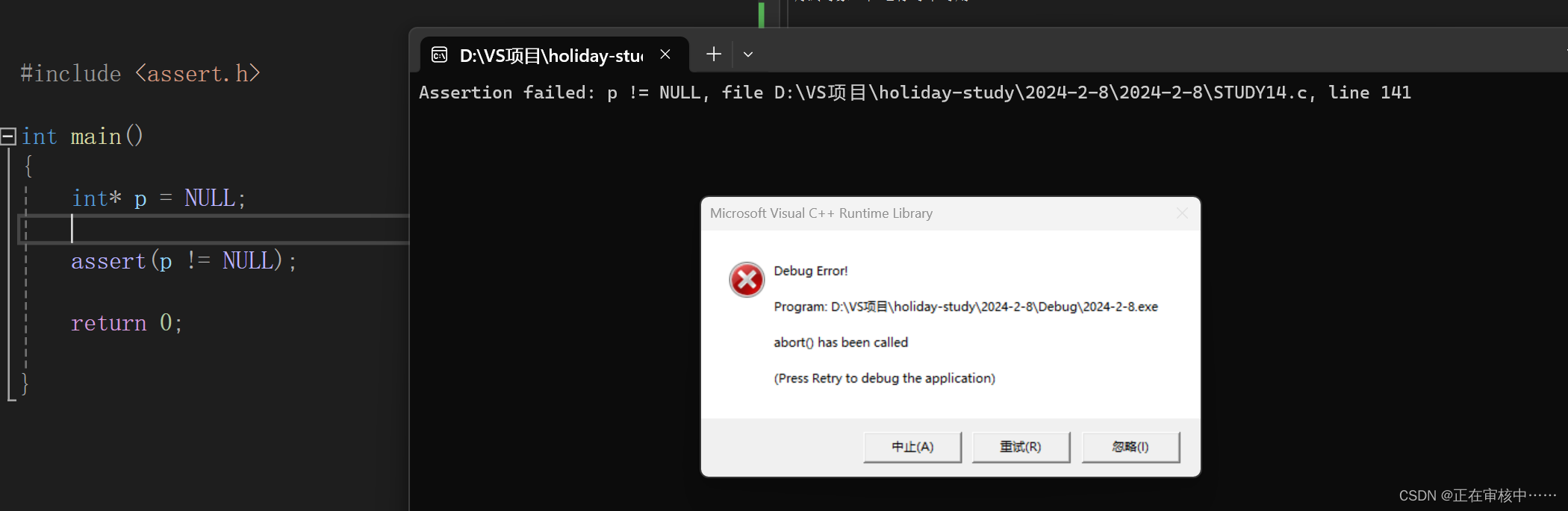
详解C语言中的野指针和assert断言
目录 1.野指针1.1 野指针成因1.1.1 指针未初始化1.1.2 指针越界访问1.1.3 指针指向的空间释放 1.2 如何规避野指针1.2.1 指针初始化1.2.2 小心指针越界1.2.3 指针变量不再使用时,及时置为NULL,指针使用之前检查1.2.4 避免返回局部变量的地址 2.assert断言…...
)
Vue源码系列讲解——模板编译篇【四】(文本解析器)
1. 前言 在上篇文章中我们说了,当HTML解析器解析到文本内容时会调用4个钩子函数中的chars函数来创建文本型的AST节点,并且也说了在chars函数中会根据文本内容是否包含变量再细分为创建含有变量的AST节点和不包含变量的AST节点,如下ÿ…...
微信小程序开发学习笔记《17》uni-app框架-tabBar
微信小程序开发学习笔记《17》uni-app框架-tabBar 博主正在学习微信小程序开发,希望记录自己学习过程同时与广大网友共同学习讨论。建议仔细阅读uni-app对应官方文档 一、创建tabBar分支 运行如下的命令,基于master分支在本地创建tabBar子分支&#x…...

《区块链公链数据分析简易速速上手小册》第5章:高级数据分析技术(2024 最新版)
文章目录 5.1 跨链交易分析5.1.1 基础知识5.1.2 重点案例:分析以太坊到 BSC 的跨链交易理论步骤和工具准备Python 代码示例构思步骤1: 设置环境和获取合约信息步骤2: 分析以太坊上的锁定交易步骤3: 跟踪BSC上的铸币交易 结论 5.1.3 拓展案例 1:使用 Pyth…...
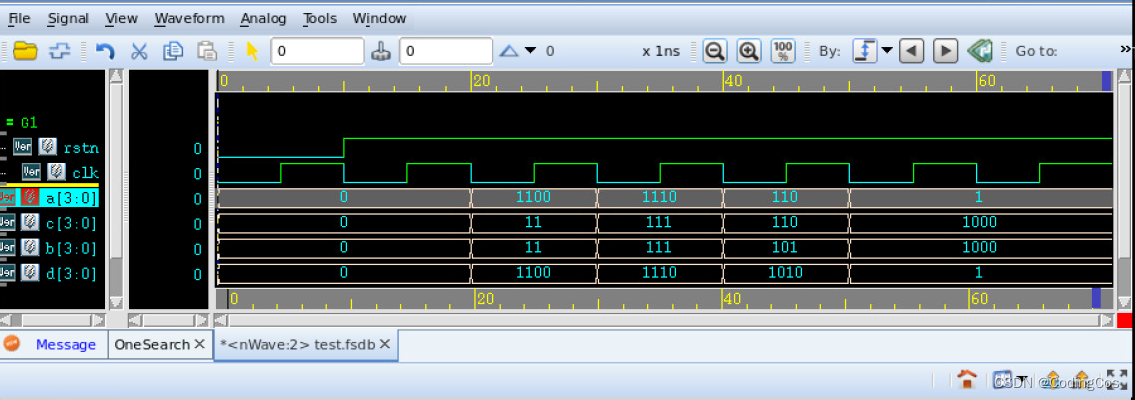
【芯片设计- RTL 数字逻辑设计入门 15 -- 函数实现数据大小端转换】
文章目录 函数实现数据大小端转换函数语法函数使用的规则Verilog and Testbench综合图VCS 仿真波形 函数实现数据大小端转换 在数字芯片设计中,经常把实现特定功能的模块编写成函数,在需要的时候再在主模块中调用,以提高代码的复用性和提高设…...

Codeforces Round 925 (Div. 3) D. Divisible Pairs (Java)
Codeforces Round 925 (Div. 3) D. Divisible Pairs (Java) 比赛链接:Codeforces Round 925 (Div. 3) D题传送门:D.Divisible Pairs 题目:D.Divisible Pairs 题目描述 输出格式 For each test case, output a single integer — the num…...

【C语言】实现单链表
目录 (一)头文件 (二)功能实现 (1)打印单链表 (2)头插与头删 (3)尾插与尾删 (4) 删除指定位置节点 和 删除指定位置之后的节点 …...

Hive调优——合并小文件
目录 一、小文件产生的原因 二、小文件的危害 三、小文件的解决方案 3.1 小文件的预防 3.1.1 减少Map数量 3.1.2 减少Reduce的数量 3.2 已存在的小文件合并 3.2.1 方式一:insert overwrite (推荐) 3.2.2 方式二:concatenate 3.2.3 方式三ÿ…...
责任链模式)
设计模式(行为型模式)责任链模式
目录 一、简介二、责任链模式2.1、处理器接口2.2、具体处理器类2.3、使用 三、优点与缺点 一、简介 责任链模式(Chain of Responsibility Pattern)是一种行为设计模式,允许你将请求沿着处理者链进行传递,直到有一个处理者能够处理…...
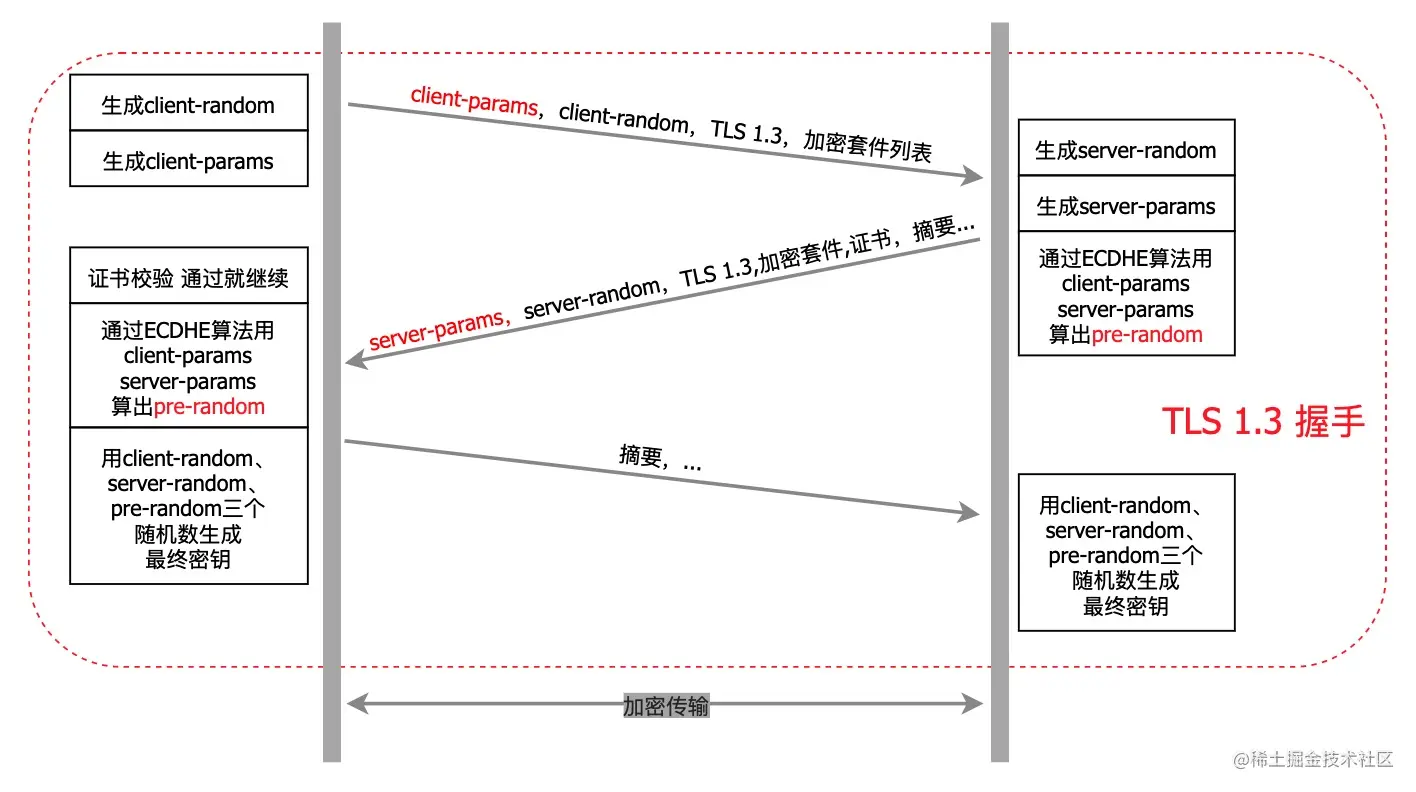
HTTP和HTTPS区别!
http 是我们几乎天天都要打交道的东西,相关知识点有点多,所以也有不少面试必问的点,这里做了一些整理,帮且大家树立完整的 http 知识体系,对面试官说 so easy HTTP 的特点和缺点 特点:无连接、无状态、灵…...
)
麻将普通胡牌算法(带混)
最近在玩腾讯的麻将游戏,但是经常需要充值,于是就想自己实现一个简单的单机麻将游戏.第一个难点就是实现胡牌的判断.这里写一下心得. 术语 本文的胡牌是指手牌构成了3N2的牌型,即一对做将,剩下的牌均为刻子(3张一样的牌)或者顺子(3张连续的牌比如234饼). 下面就是一个14张牌…...

Rust结构体详解:定义、使用及方法
Rust 是一门强调安全性和性能的系统级编程语言,它引入了结构体(struct)作为一种自定义的数据类型,允许程序员以更加灵活的方式组织和操作数据。在本篇博客中,我们将深入探讨 Rust 结构体的定义、使用以及相关概念。 什…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...
