Linux内核与驱动面试经典“小”问题集锦(6)
接前一篇文章:Linux内核与驱动面试经典“小”问题集锦(5)
问题8
问:如何判断一个数是否是2的幂次(假设最多32位)?
备注:此问题是笔者年前参加小米面试时遇到的一个问题,是属于面试中的笔试。原题是一语句实现y是否为2的若干次幂的判断。
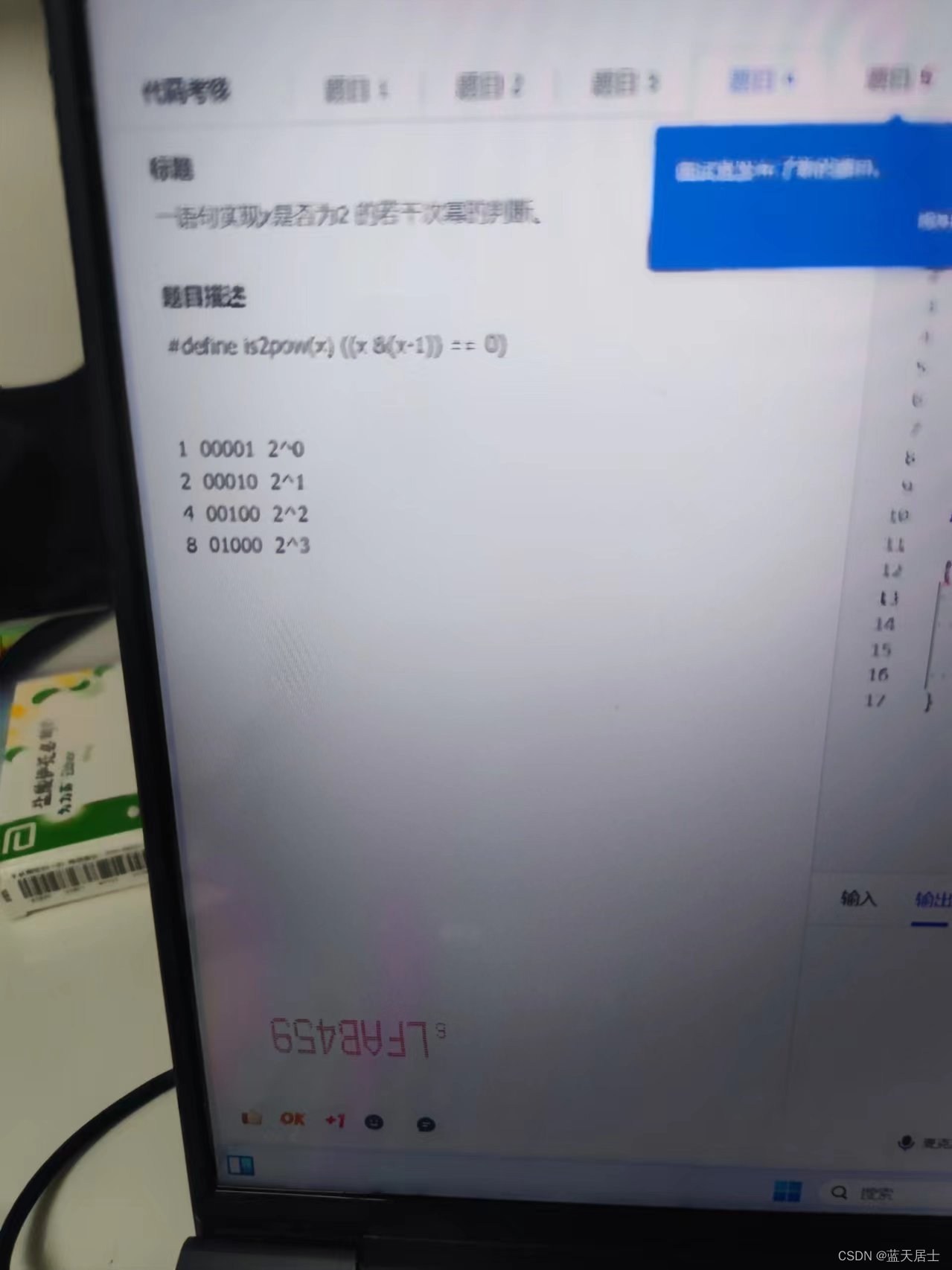
答:
其实上图中已经提供了一些思路,先要观察规律(为了简化,以8位为例):
正例:
1:0x01即0b00000001,2的0次幂
2:0x02即0b00000010,2的1次幂
4:0x04即0b00000100,2的2次幂
……
128:0x80即0b10000000,2的7次幂
反例:
3:0x03即0b00000011
5:0x05即0b00000101
6:0x06即0b00000110
7:0x07即0b00000111
当时那为面试官还蛮有耐心,还提示到要从本数和其掩码的方面考虑。不过本人资质比较愚钝,一时也没有找到规律。他后来直接给出了答案,也就是上图中的那个:
#define is2pow(x) ((x & (x-1)) == 0)验证:
- x=1时,x & (x-1)为0,返回真,说明是2的幂次。
- x=2时,x & (x-1)为0,返回真,说明是2的幂次。
- x=4时,x & (x-1)为0,返回真,说明是2的幂次。
- x=8时,x & (x-1)为0,返回真,说明是2的幂次。
- x=3时,x & (x-1)为2,返回假,说明不是2的幂次。
- x=5时,x & (x-1)为4,返回假,说明不是2的幂次。
- x=6时,x & (x-1)为4,返回假,说明不是2的幂次。
- x=7时,x & (x-1)为6,返回假,说明不是2的幂次。
总结:
这道题背后考察的不光是候选者的智商和数字敏感性,而更多地是考察内核的功力,因为Linux内核中有很多基于2的幂次的判断。对于此不熟悉,说明对于内核与驱动看得不够透彻、不够精通。
问题9
问:container_of内核中经常遇到吧,请写出其具体的代码实现?
备注:此问题是笔者年前参加小米面试时遇到的一个问题,是属于面试中的笔试。笔者几年之前参加位于北京玉泉慧谷的一家公司(公司名字已不记得了,只记得地点)面试的时候,也被问到过这个问题,不过当时只是和面试官说了思路,并没有直接写出完整代码。
答:
container_of(ptr, type, member)宏的作用是通过结构体成员的地址和结构体类型推导出结构体的地址,type是指结构体的类型,member是成员在结构体中的名字,ptr是该成员在type结构体中的地址。
实际上笔者多年来看内核的代码经常会遇到container_of,也花时间研究过代码,尤其是之前面试中被问到时,面试结束回来后曾经认真研究过一番。但是几次都是当时弄得很明白,时间一长就淡忘了。并不能做到信手拈来,这也应该是不经常玩内核的一种不足。
笔者在小米面试时被问到这个问题后,就努力在脑海中回忆container_of这个宏的具体实现。依稀记得是这样:
#define container_of(pointer, structure, member) (structure *)(pointer - (&((structure *)0)->member))这是当时笔者第一时间想出来的。但是并不完全正确。
当时面试官说,要实现container_of宏,必须先实现offset_off宏,因此笔者就没有直接给出container_of的实现,而是按照面试官的思路即要求,先写出了offset_off宏,如下:
#define offset_off(structure, member) (&(((structure *)NULL)->member))这样写完了之后,面试官指出了不足,应该将偏移强制转换为int类型,如下:
#define offset_off(structure, member) ((int)(&((structure *)NULL)->member))完成了offset_off宏之后,进一步再实现container_of宏,我开始的实现是这样:
#define container_of(pointer, structure, member) ((int)(pointer) - offset_off(structure, member))面试官又指出了一处不足,应该强制转换为void *类型,更正后实现如下:
#define container_of(pointer, structure, member) (void *)((int)(pointer) - offset_off(structure, member))将offset_off宏完全展开后,最终得到:
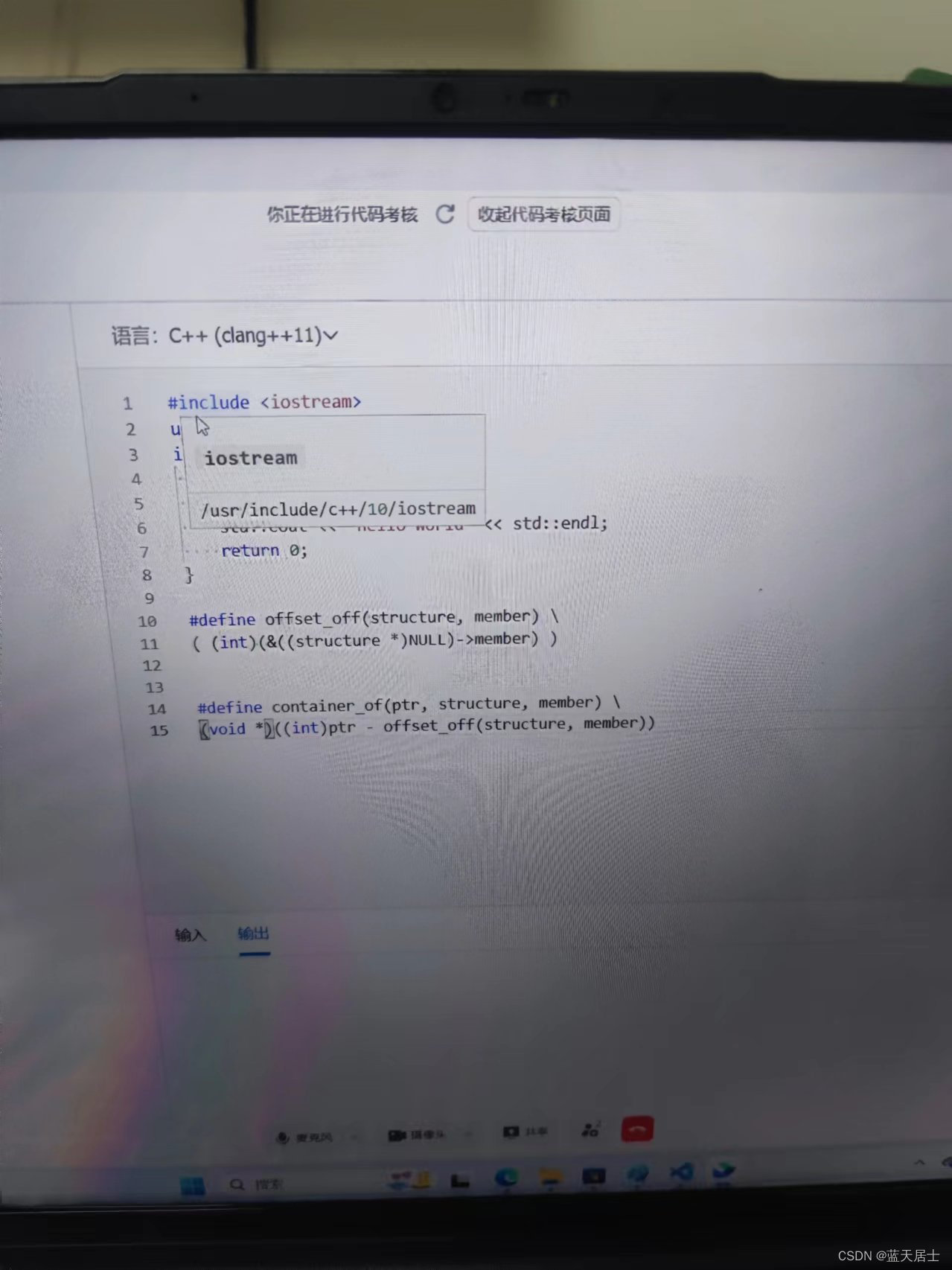
#define container_of(pointer, structure, member) (void *)((int)(pointer) - ((int)(&((structure *)NULL)->member)))和笔者最开始所构想的进行对比:
- 最初构想的:
#define container_of(pointer, structure, member) (structure *)(pointer - (&((structure *)0)->member))
- 最终实现的:
#define container_of(pointer, structure, member) (void *)((int)(pointer) - ((int)(&((structure *)0)->member)))
总结:
通过以上过程可以发现,虽然在大方向上能够答出,但在细节、精细度上和大公司那些人还是有一些差距,这是今后做技术需要弥补的。
在此顺带给出Linux内核中container_of宏的完整实现,在include/linux/container_of.h中(实际上内核中有多处实现,但最为“正宗”的是这一个),代码如下:
/*** container_of - cast a member of a structure out to the containing structure* @ptr: the pointer to the member.* @type: the type of the container struct this is embedded in.* @member: the name of the member within the struct.** WARNING: any const qualifier of @ptr is lost.*/
#define container_of(ptr, type, member) ({ \void *__mptr = (void *)(ptr); \static_assert(__same_type(*(ptr), ((type *)0)->member) || \__same_type(*(ptr), void), \"pointer type mismatch in container_of()"); \((type *)(__mptr - offsetof(type, member))); })这个正宗的container_of的定义比较复杂,换一个相对比较好理解的版本,在tools/include/linux/kernel.h中,代码如下:
#define offsetof(TYPE, MEMBER) ((size_t) &((TYPE *)0)->MEMBER)/*** container_of - cast a member of a structure out to the containing structure* @ptr: the pointer to the member.* @type: the type of the container struct this is embedded in.* @member: the name of the member within the struct.**/
#define container_of(ptr, type, member) ({ \const typeof(((type *)0)->member) * __mptr = (ptr); \(type *)((char *)__mptr - offsetof(type, member)); })对比:
相关文章:

Linux内核与驱动面试经典“小”问题集锦(6)
接前一篇文章:Linux内核与驱动面试经典“小”问题集锦(5) 问题8 问:如何判断一个数是否是2的幂次(假设最多32位)? 备注:此问题是笔者年前参加小米面试时遇到的一个问题,…...
-钉钉告警企业微信配置)
【zabbix】(四)-钉钉告警企业微信配置
前提条件: 已经安装了Python3环境(脚本需要requests模块)。Centos7.x自带Python2(不含requests模块) 钉钉告警配置 一 安装Python3 参考该优秀文档部署 查看Python的模块:pip list / pip3 list 报错 …...
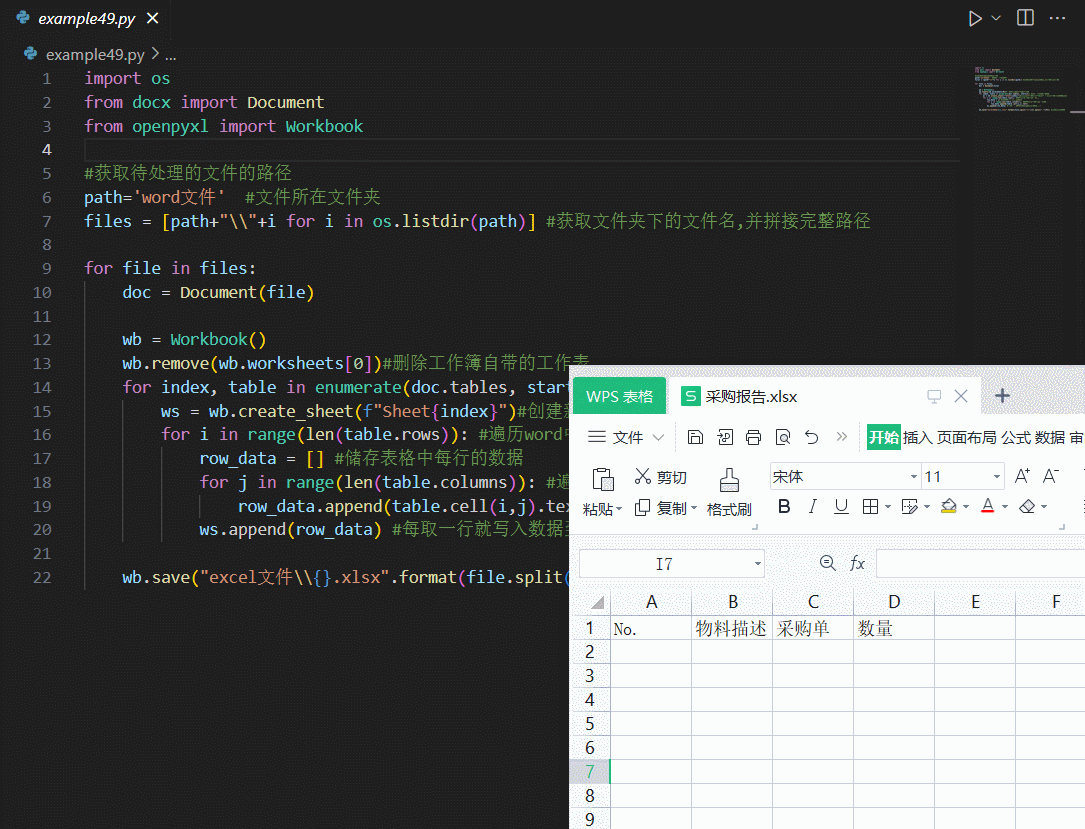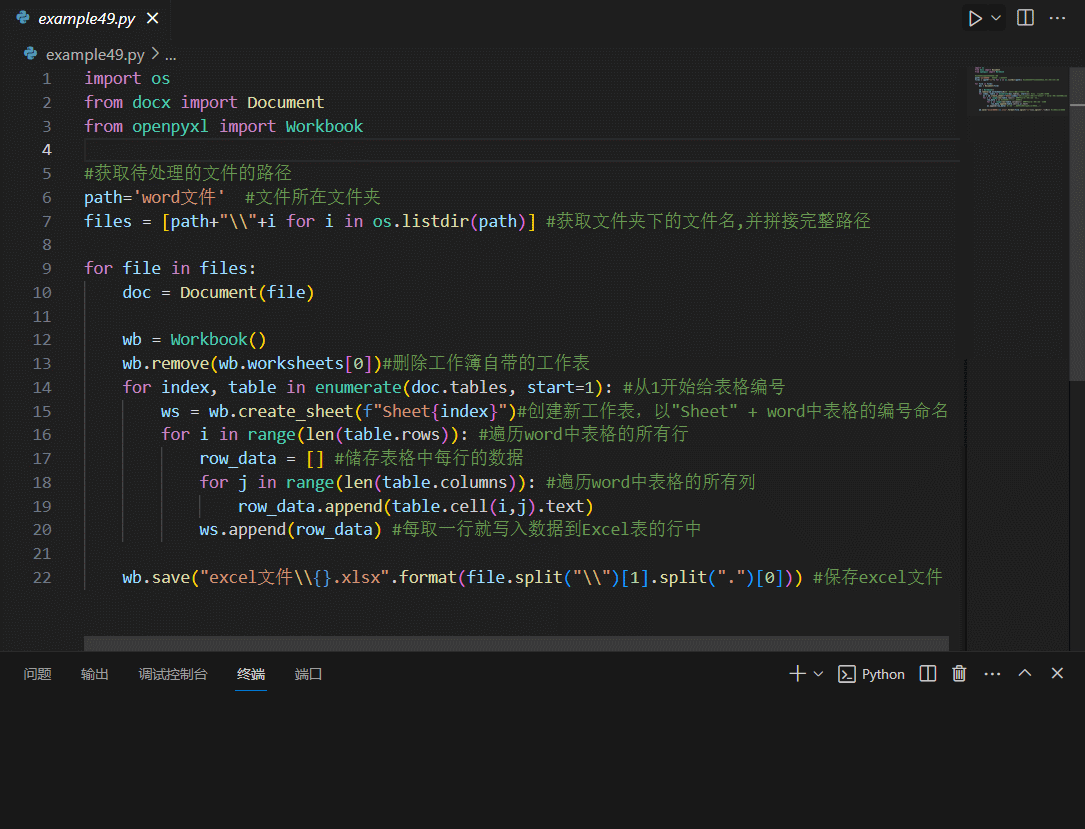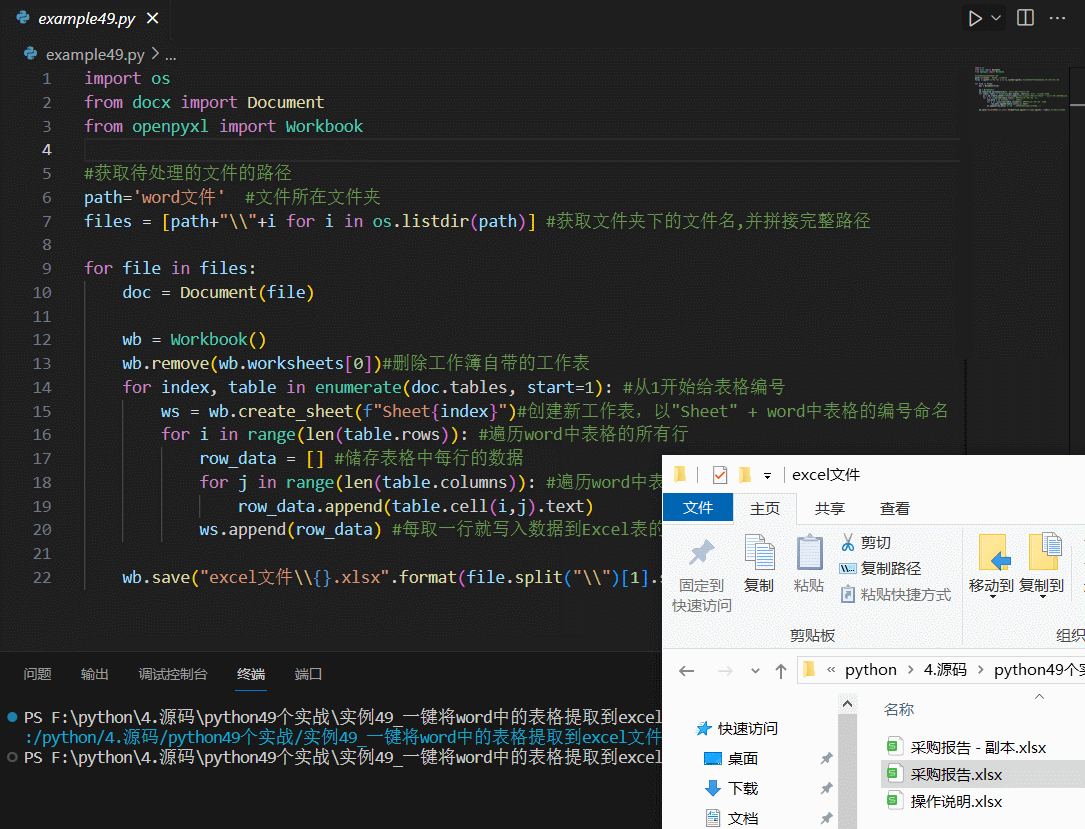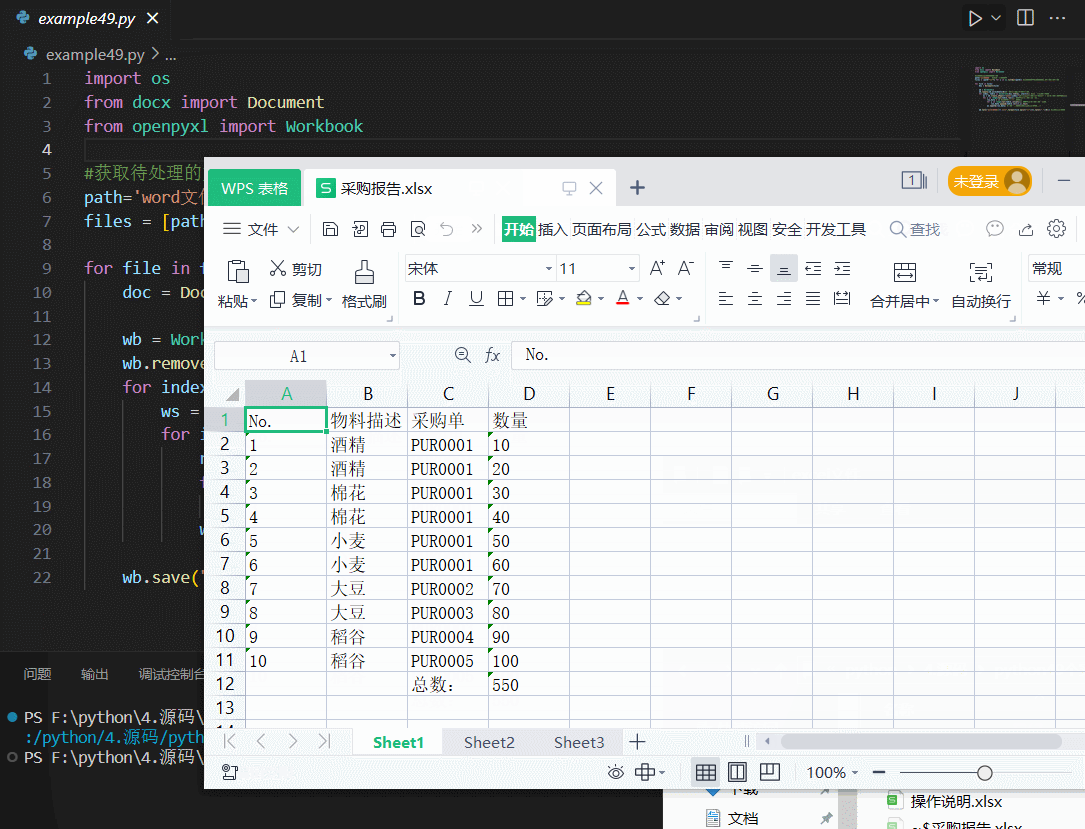
python-自动化篇-办公-一键将word中的表格提取到excel文件中
文章目录 代码 工作中,经常需要将Word文档中的表格粘贴到Excel文件中,以便汇总及分析。一个一个复制粘贴,非常不方便,还是Python自动化操作,省心省力。要求如下图所示,即将word中的所有表格,转存…...
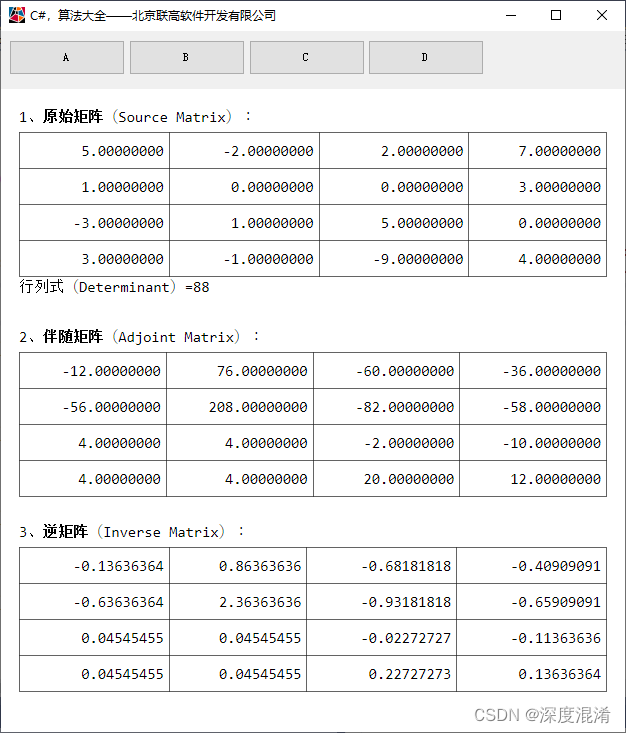
C#,数值计算,矩阵的行列式(Determinant)、伴随矩阵(Adjoint)与逆矩阵(Inverse)的算法与源代码
本文发布矩阵(Matrix)的一些初级算法。 一、矩阵的行列式(Determinant) 矩阵行列式是指矩阵的全部元素构成的行列式,设A(a)是数域P上的一个n阶矩阵,则所有A(a)中的元素组成的行列式称为矩阵A的行列式&…...
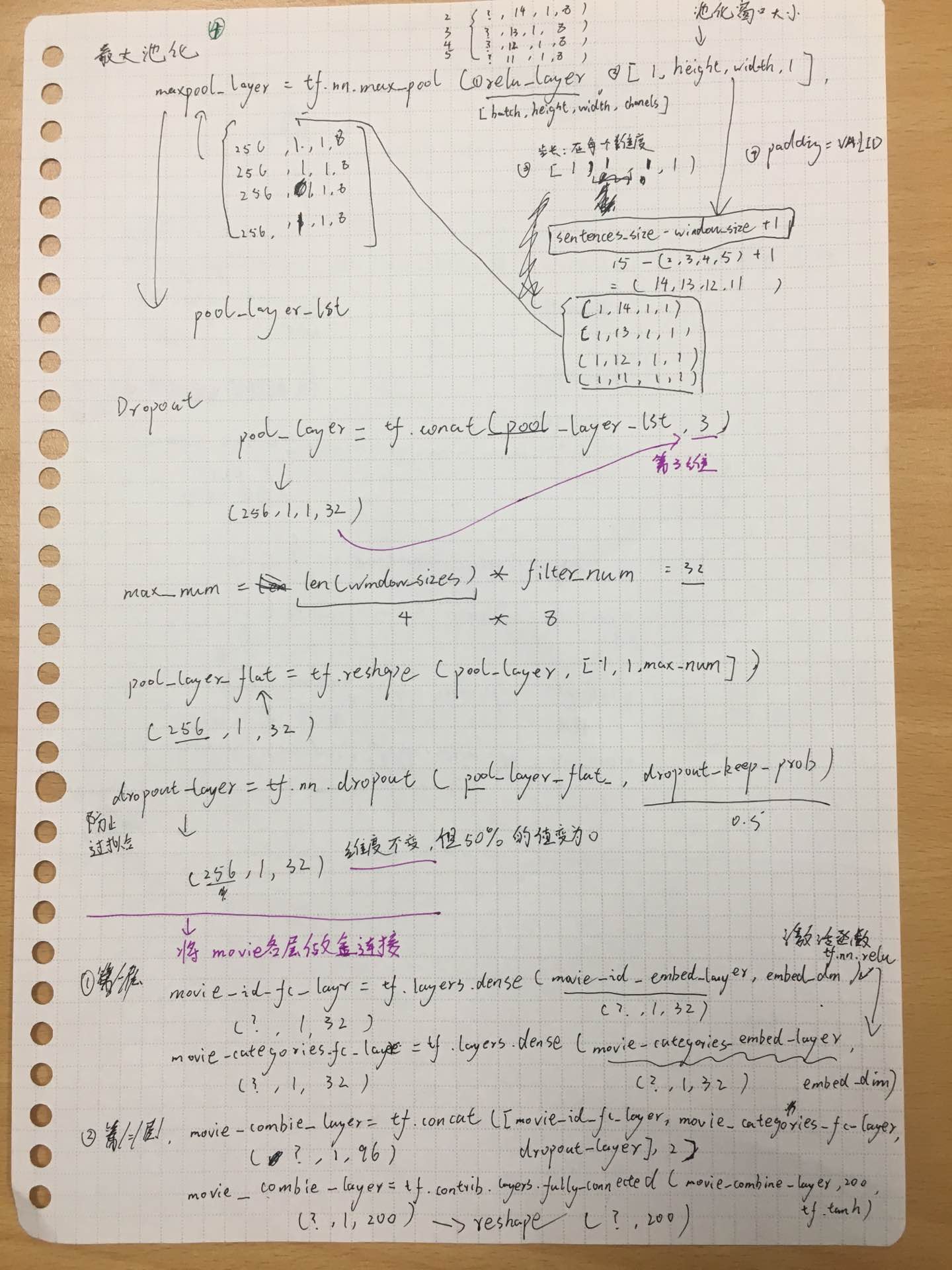
人工智能|推荐系统——基于tensorflow的个性化电影推荐系统实战(有前端)
代码下载: 基于tensorflow的个性化电影推荐系统实战(有前端).zip资源-CSDN文库 项目简介: dl_re_web : Web 项目的文件夹re_sys: Web app model:百度云下载之后,把model放到该文件夹下recommend: 网络模型相…...
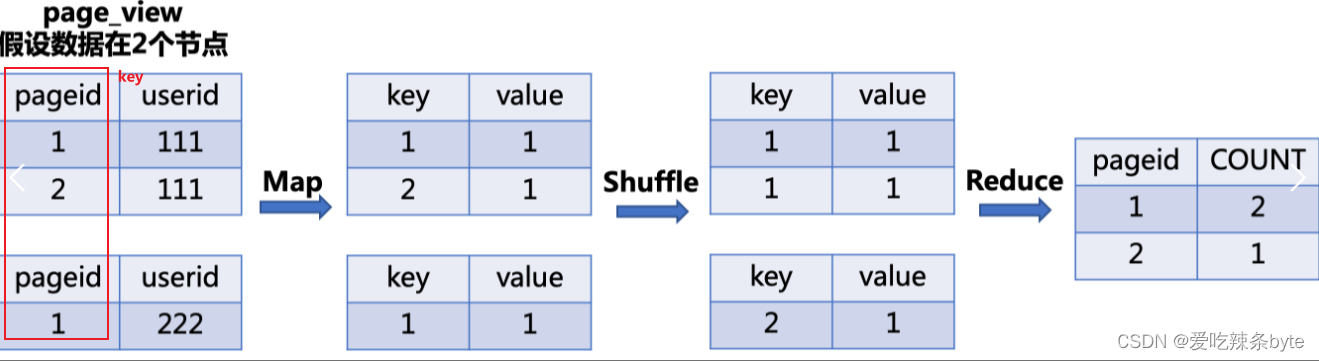
Hive SQL编译成MapReduce任务的过程
目录 一、架构及组件介绍 1.1 Hive底层架构 1.2 Hive组件 1.3 Hive与Hadoop交互过程 二、Hive SQL 编译成MR任务的流程 2.1 HQL转换为MR源码整体流程介绍 2.2 程序入口—CliDriver 2.3 HQL编译成MR任务的详细过程—Driver 2.3.1 将HQL语句转换成AST抽象语法树 词法、语…...

【C++】快速上手map、multimap、set、multiset
文章目录 一、前言二、set / multiset1. 常见应用2. 核心操作 三、map / multimap1. 常见应用2. 核心操作 一、前言 S T L STL STL 中的关联式容器分为树型结构和哈希结构,树型结构主要有四种: s e t set set、 m u l t i s e t multiset multiset、 m a…...
【分享】图解ADS+JLINK调试ARM
文章是对LPC2148而写的,但是对三星的44B0芯片同样适用,只需要在选择时将相应的CPU选择的S3C44B0就可以了。 JLINK在ADS下调试心得 前两天一个客户用jlink在ADS下调试LPC2148总报错,这个错误我之前在调试LPC2200的时候也碰到过,后…...
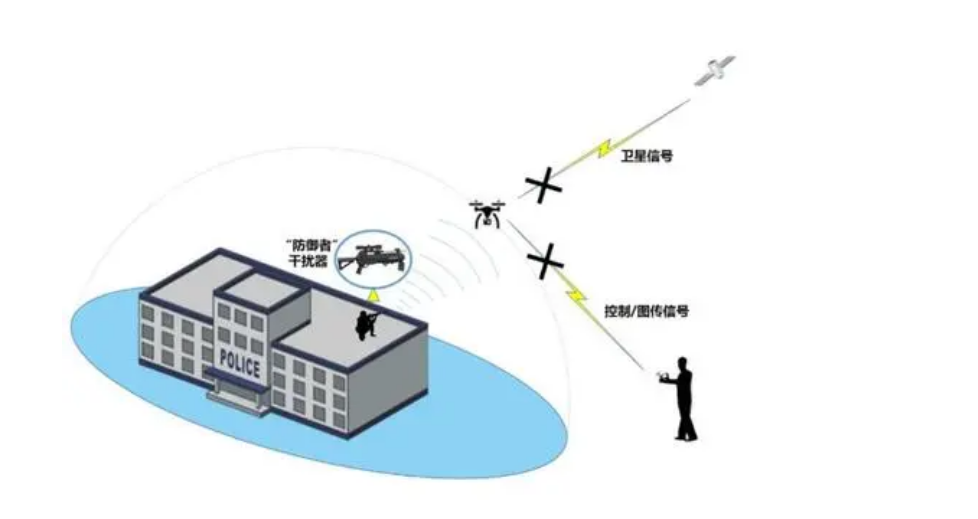
反无人机系统技术分析,无人机反制技术理论基础,无人机技术详解
近年来,经过大疆、parrot、3d robotics等公司不断的努力,具有强大功能的消费级无人机价格不断降低,操作简便性不断提高,无人机正快速地从尖端的军用设备转入大众市场,成为普通民众手中的玩具。 然而,随着消…...
Kotlin和Java 单例模式
Java 和Kotlin的单例模式其实很像,只是Kotlin一部分单例可以用对象类和委托lazy来实现 Java /*** 懒汉式,线程不安全*/ class Singleton {private static Singleton instance;private Singleton() {}public static Singleton getInstance() {if (insta…...
)
软考 系统分析师系列知识点之信息系统战略规划方法(9)
接前一篇文章:软考 系统分析师系列知识点之信息系统战略规划方法(8) 所属章节: 第7章. 企业信息化战略与实施 第4节. 信息系统战略规划方法 7.4.5 信息工程方法 信息工程(Information Engineering,IE&…...
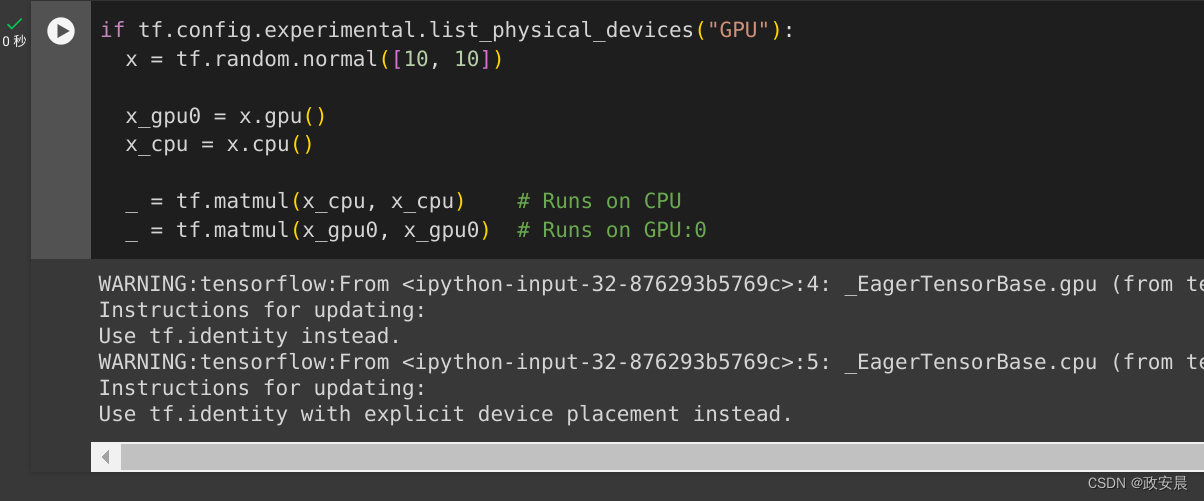
政安晨:示例演绎TensorFlow的官方指南(一){基础知识}
为什么要示例演绎? 既然有了官方指南,咱们在官方指南上看看就可以了,为什么还要写示例演绎的文章呢? 其实对于初步了解TensorFlow的小伙伴们而言,示例演绎才是最重要的。 官方文档已经假定了您已经具备了相当合适的…...

node - 与数据库交互
在Web开发中,与数据库交互是常见的需求,用于持久化存储、检索和操作数据。不同的后端技术和数据库类型(如关系型数据库和非关系型数据库)有着不同的交互方式。下面介绍几种常见的数据库交互方法。 关系型数据库 关系型数据库(如MySQL、PostgreSQL、SQLite)使用结构化查…...

速盾:2024年cdn在5g时代重要吗
在2024年,随着5G技术的普及与应用,内容分发网络(Content Delivery Network,CDN)在数字化时代中的重要性将进一步巩固和扩大。CDN是一种用于快速、高效地分发网络内容的基础设施,它通过将内容部署在全球各地…...
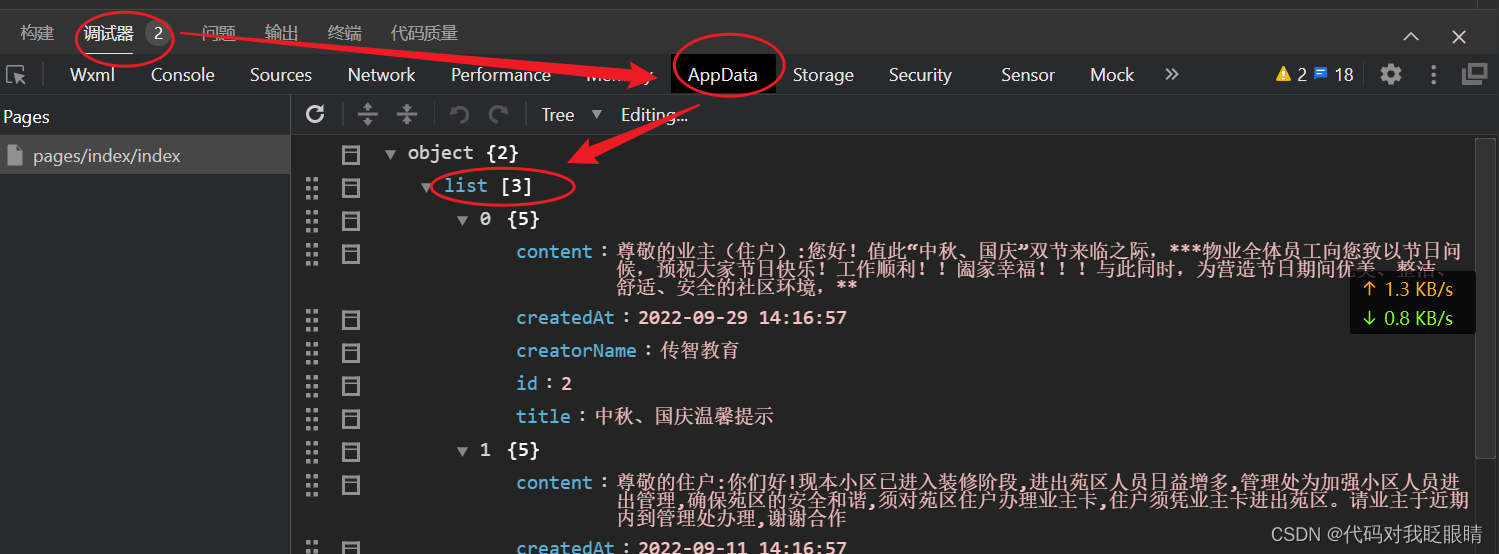
微信小程序(四十一)wechat-http的使用
注释很详细,直接上代码 上一篇 新增内容: 1.模块下载 2.模块的使用 在终端输入npm install wechat-http 没有安装成功vue的先看之前的一篇 微信小程序(二十)Vant组件库的配置- 如果按以上的成功配置出现如下报错先输入以下语句 …...

所有设计模式大全及学习链接
文章目录 创建型设计模式结构型设计模式行为型设计模式 创建型设计模式 一种创建对象的设计模式,它们提供了一种灵活的方式来创建对象,同时隐藏了对象的创建细节。以下是常见的创建型设计模式: 工厂方法模式(Factory Method Patte…...
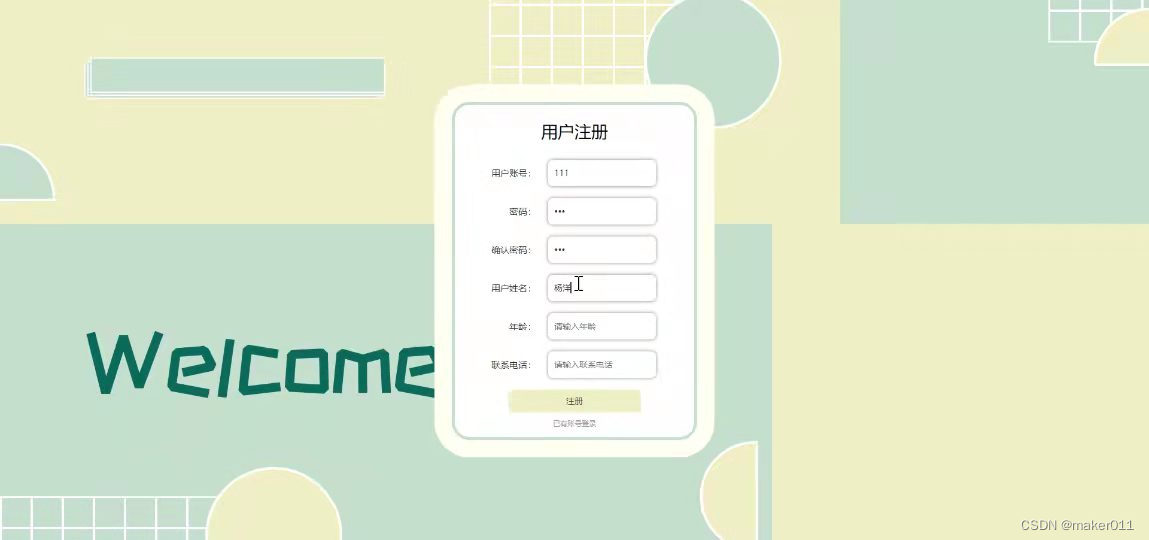
【Java程序设计】【C00264】基于Springboot的原创歌曲分享平台(有论文)
基于Springboot的原创歌曲分享平台(有论文) 项目简介项目获取开发环境项目技术运行截图 项目简介 这是一个基于Springboot的原创歌曲分享平台 本系统分为平台功能模块、管理员功能模块以及用户功能模块。 平台功能模块:在平台首页可以查看首…...

2024年,要特别注意这两个方位
家居风水对每个家庭都非常重要,可在无形中影响到人们的事业、财富以及健康运势。俗话说:“风水轮流转”,2024年为甲辰龙年,斗转星移、九宫飞星将改变宫位,新一年的磁场即将启动,方位的吉凶也会重新变动&…...
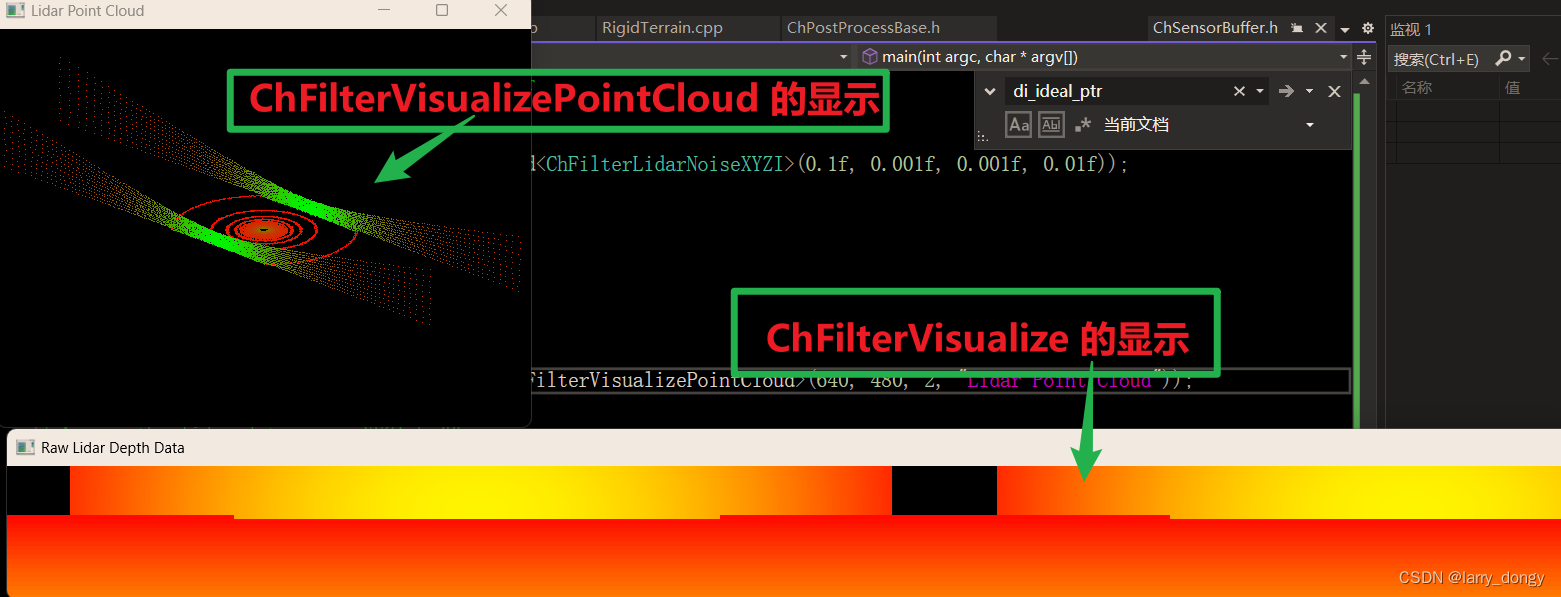
【Chrono Engine学习总结】5-sensor-5.1-sensor基础并创建一个lidar
由于Chrono的官方教程在一些细节方面解释的并不清楚,自己做了一些尝试,做学习总结。 1、Sensor模块 Sensor模块是附加模块,需要单独安装。参考:【Chrono Engine学习总结】1-安装配置与程序运行 Sensor Module Tutorial Sensor …...

springboot/ssm学生信息管理系统Java学生在线选课考试管理系统
springboot/ssm学生信息管理系统Java学生在线选课考试管理系统 开发语言:Java 框架:springboot(可改ssm) vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql 5.…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...
