C#,数值计算,矩阵的行列式(Determinant)、伴随矩阵(Adjoint)与逆矩阵(Inverse)的算法与源代码

本文发布矩阵(Matrix)的一些初级算法。
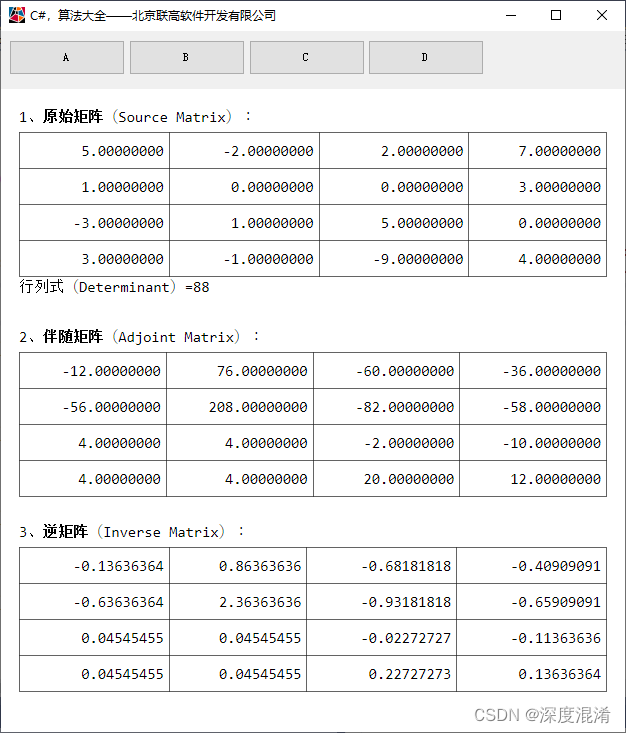
一、矩阵的行列式(Determinant)
矩阵行列式是指矩阵的全部元素构成的行列式,设A=(a)是数域P上的一个n阶矩阵,则所有A=(a)中的元素组成的行列式称为矩阵A的行列式,记为|A|或det(A)。若A,B是数域P上的两个n阶矩阵,k是P中的任一个数,则|AB|=|A||B|,|kA|=kⁿ|A|,|A*|=|A|,其中A*是A的伴随矩阵;若A是可逆矩阵,则|A|=|A|。
/// <summary>
/// 计算 A[p,q] 位于 [,]temp 的块辅因子
/// </summary>
/// <param name="matrix"></param>
/// <param name="temp"></param>
/// <param name="p"></param>
/// <param name="q"></param>
/// <param name="n"></param>
private static void BlockCofactor(double[,] matrix, ref double[,] temp, int p, int q, int n)
{
int i = 0;
int j = 0;
for (int row = 0; row < n; row++)
{
for (int col = 0; col < n; col++)
{
if (row != p && col != q)
{
temp[i, j++] = matrix[row, col];
if (j == (n - 1))
{
j = 0;
i++;
}
}
}
}
}
/// <summary>
/// 求矩阵行列式(递归算法)
/// </summary>
/// <param name="N"></param>
/// <param name="matrix"></param>
/// <param name="n"></param>
/// <returns></returns>
public static double Determinant(int N, double[,] matrix, int n)
{
if (n == 1)
{
return matrix[0, 0];
}
double D = 0.0;
double[,] temp = new double[N, N];
int sign = 1;
for (int f = 0; f < n; f++)
{
BlockCofactor(matrix, ref temp, 0, f, n);
D += sign * matrix[0, f] * Determinant(N, temp, n - 1);
sign = -sign;
}
return D;
}
/// <summary>
/// 计算 A[p,q] 位于 [,]temp 的块辅因子
/// </summary>
/// <param name="matrix"></param>
/// <param name="temp"></param>
/// <param name="p"></param>
/// <param name="q"></param>
/// <param name="n"></param>
private static void BlockCofactor(double[,] matrix, ref double[,] temp, int p, int q, int n)
{int i = 0;int j = 0;for (int row = 0; row < n; row++){for (int col = 0; col < n; col++){if (row != p && col != q){temp[i, j++] = matrix[row, col];if (j == (n - 1)){j = 0;i++;}}}}
}/// <summary>
/// 求矩阵行列式(递归算法)
/// </summary>
/// <param name="N"></param>
/// <param name="matrix"></param>
/// <param name="n"></param>
/// <returns></returns>
public static double Determinant(int N, double[,] matrix, int n)
{if (n == 1){return matrix[0, 0];}double D = 0.0;double[,] temp = new double[N, N];int sign = 1;for (int f = 0; f < n; f++){BlockCofactor(matrix, ref temp, 0, f, n);D += sign * matrix[0, f] * Determinant(N, temp, n - 1);sign = -sign;}return D;
}二、矩阵的伴随矩阵(Adjoint Matrix)
一个方形矩阵的伴随矩阵是一个类似于逆矩阵的概念。如果二维矩阵可逆,那么它的逆矩阵和它的伴随矩阵之间只差一个系数,对多维矩阵也存在这个规律。然而,伴随矩阵对不可逆的矩阵也有定义,并且不需要用到除法。
/// <summary>
/// 伴随矩阵
/// </summary>
/// <param name="A"></param>
/// <param name="adj"></param>
public static void Adjoint(double[,] matrix, out double[,] adjoint)
{
int N = matrix.GetLength(0);
adjoint = new double[N, N];
if (N == 1)
{
adjoint[0, 0] = 1.0;
return;
}
int sign = 1;
double[,] temp = new double[N, N];
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
BlockCofactor(matrix, ref temp, i, j, N);
sign = ((i + j) % 2 == 0) ? 1 : -1;
adjoint[j, i] = (sign) * (Determinant(N, temp, N - 1));
}
}
}
/// <summary>
/// 伴随矩阵
/// </summary>
/// <param name="A"></param>
/// <param name="adj"></param>
public static void Adjoint(double[,] matrix, out double[,] adjoint)
{int N = matrix.GetLength(0);adjoint = new double[N, N];if (N == 1){adjoint[0, 0] = 1.0;return;}int sign = 1;double[,] temp = new double[N, N];for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){BlockCofactor(matrix, ref temp, i, j, N);sign = ((i + j) % 2 == 0) ? 1 : -1;adjoint[j, i] = (sign) * (Determinant(N, temp, N - 1));}}
}三、矩阵的逆矩阵(Inverse Matrix)
设A是一个n阶矩阵,若存在另一个n阶矩阵B,使得: AB=BA=E ,则称方阵A可逆,并称方阵B是A的逆矩阵。矩阵求逆,即求矩阵的逆矩阵。矩阵是线性代数的主要内容,很多实际问题用矩阵的思想去解既简单又快捷。逆矩阵又是矩阵理论的很重要的内容,逆矩阵的求法自然也就成为线性代数研究的主要内容之一。
/// <summary>
/// 矩阵求逆
/// </summary>
/// <param name="A"></param>
/// <param name="inverse"></param>
/// <returns></returns>
public static bool Inverse(double[,] matrix, out double[,] inverse)
{
int N = matrix.GetLength(0);
inverse = new double[N, N];
double det = Determinant(N, matrix, N);
if (det == 0)
{
return false;
}
Adjoint(matrix, out double[,] adj);
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
inverse[i, j] = adj[i, j] / (double)det;
}
}
return true;
}
/// <summary>
/// 矩阵求逆
/// </summary>
/// <param name="A"></param>
/// <param name="inverse"></param>
/// <returns></returns>
public static bool Inverse(double[,] matrix, out double[,] inverse)
{int N = matrix.GetLength(0);inverse = new double[N, N];double det = Determinant(N, matrix, N);if (det == 0){return false;}Adjoint(matrix, out double[,] adj);for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){inverse[i, j] = adj[i, j] / (double)det;}}return true;
}
演算代码:
private void button1_Click(object sender, EventArgs e)
{
double[,] A = {
{5, -2, 2, 7},
{1, 0, 0, 3},
{-3, 1, 5, 0},
{3, -1, -9, 4}
};
double d = Algorithm_Gallery.Determinant(4, A, 4);
StringBuilder sb = new StringBuilder();
sb.Append(Welcome());
sb.AppendLine("1、<b>原始矩阵</b>(Source Matrix):<br>");
sb.Append(Algorithm_Gallery.ToHtml(A));
sb.AppendLine("行列式(Determinant)=" + d + "<br>");
Algorithm_Gallery.Adjoint(A, out double[,] adj);
sb.AppendLine("<br>2、<b>伴随矩阵</b>(Adjoint Matrix):<br>");
sb.Append(Algorithm_Gallery.ToHtml(adj));
Algorithm_Gallery.Inverse(A, out double[,] inv);
sb.AppendLine("<br>3、<b>逆矩阵</b>(Inverse Matrix):<br>");
sb.Append(Algorithm_Gallery.ToHtml(inv));
sb.Append(Bye());
webBrowser1.DocumentText = sb.ToString();
}
private void button1_Click(object sender, EventArgs e)
{double[,] A = { {5, -2, 2, 7},{1, 0, 0, 3},{-3, 1, 5, 0},{3, -1, -9, 4}};double d = Algorithm_Gallery.Determinant(4, A, 4);StringBuilder sb = new StringBuilder();sb.Append(Welcome());sb.AppendLine("1、<b>原始矩阵</b>(Source Matrix):<br>");sb.Append(Algorithm_Gallery.ToHtml(A));sb.AppendLine("行列式(Determinant)=" + d + "<br>");Algorithm_Gallery.Adjoint(A, out double[,] adj);sb.AppendLine("<br>2、<b>伴随矩阵</b>(Adjoint Matrix):<br>");sb.Append(Algorithm_Gallery.ToHtml(adj));Algorithm_Gallery.Inverse(A, out double[,] inv);sb.AppendLine("<br>3、<b>逆矩阵</b>(Inverse Matrix):<br>");sb.Append(Algorithm_Gallery.ToHtml(inv));sb.Append(Bye());webBrowser1.DocumentText = sb.ToString();
}打印矩阵的代码:
public static string ToHtml(double[,] y)
{
int m = y.GetLength(0);
int n = y.GetLength(1);
StringBuilder sb = new StringBuilder();
sb.AppendLine("<style>");
sb.AppendLine("td { padding:5px;text-align:right; }");
sb.AppendLine("</style>");
sb.AppendLine("<table width='100%' border=1 bordercolor='#999999' style='border-collapse:collapse;'>");
for (int i = 0; i < m; i++)
{
sb.AppendLine("<tr>");
for (int j = 0; j < n; j++)
{
sb.AppendLine("<td>" + String.Format("{0:F8}", y[i, j]) + "</td>");
}
sb.AppendLine("</tr>");
}
sb.AppendLine("</table>");
return sb.ToString();
}
————————————————————————————————
POWER BY TRUFFER.CN 50018.COM 315SOFT.COM
public static string ToHtml(double[,] y)
{int m = y.GetLength(0);int n = y.GetLength(1);StringBuilder sb = new StringBuilder();sb.AppendLine("<style>");sb.AppendLine("td { padding:5px;text-align:right; }");sb.AppendLine("</style>");sb.AppendLine("<table width='100%' border=1 bordercolor='#999999' style='border-collapse:collapse;'>");for (int i = 0; i < m; i++){sb.AppendLine("<tr>");for (int j = 0; j < n; j++){sb.AppendLine("<td>" + String.Format("{0:F8}", y[i, j]) + "</td>");}sb.AppendLine("</tr>");}sb.AppendLine("</table>");return sb.ToString();
}
相关文章:

C#,数值计算,矩阵的行列式(Determinant)、伴随矩阵(Adjoint)与逆矩阵(Inverse)的算法与源代码
本文发布矩阵(Matrix)的一些初级算法。 一、矩阵的行列式(Determinant) 矩阵行列式是指矩阵的全部元素构成的行列式,设A(a)是数域P上的一个n阶矩阵,则所有A(a)中的元素组成的行列式称为矩阵A的行列式&…...
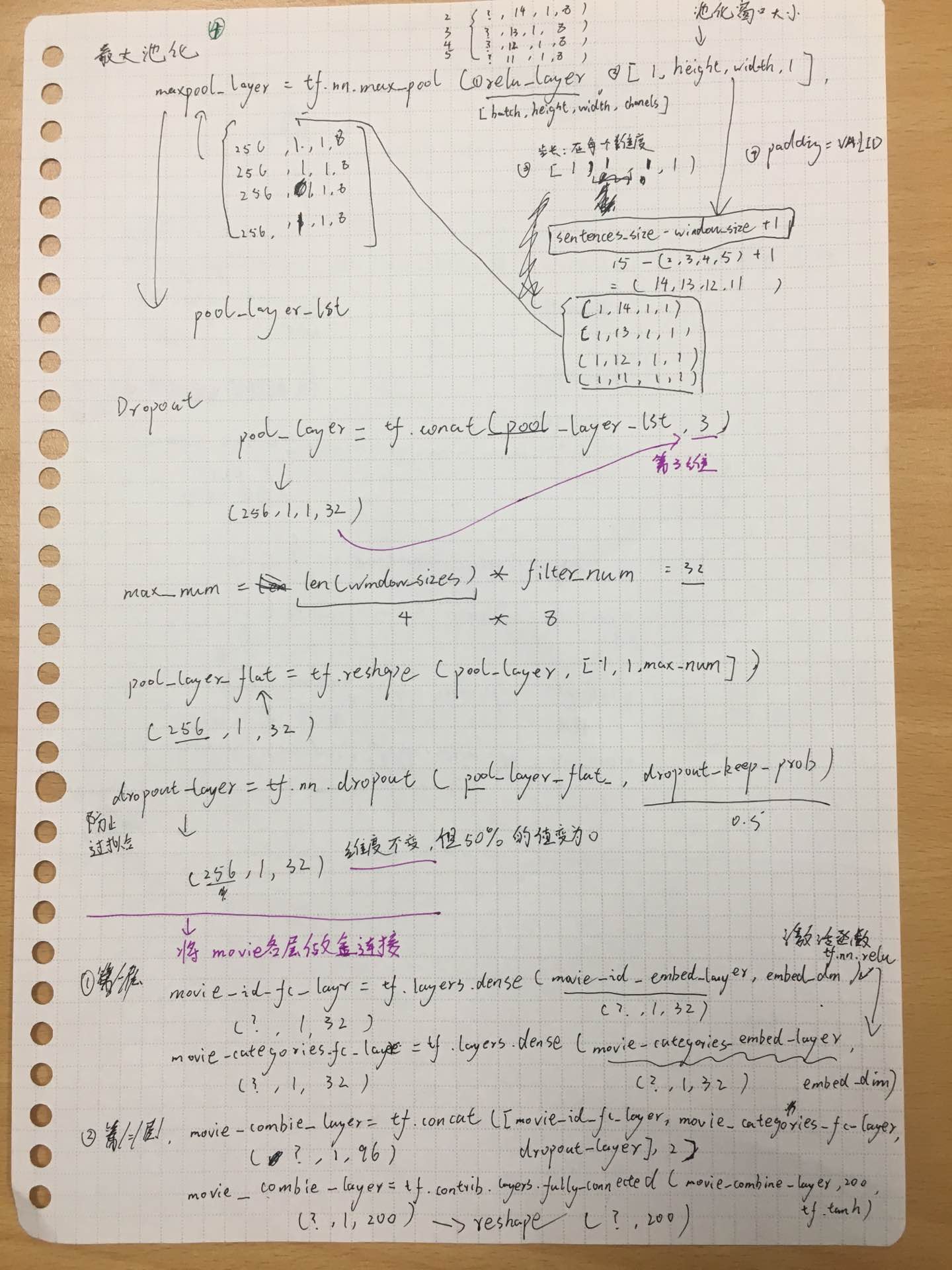
人工智能|推荐系统——基于tensorflow的个性化电影推荐系统实战(有前端)
代码下载: 基于tensorflow的个性化电影推荐系统实战(有前端).zip资源-CSDN文库 项目简介: dl_re_web : Web 项目的文件夹re_sys: Web app model:百度云下载之后,把model放到该文件夹下recommend: 网络模型相…...
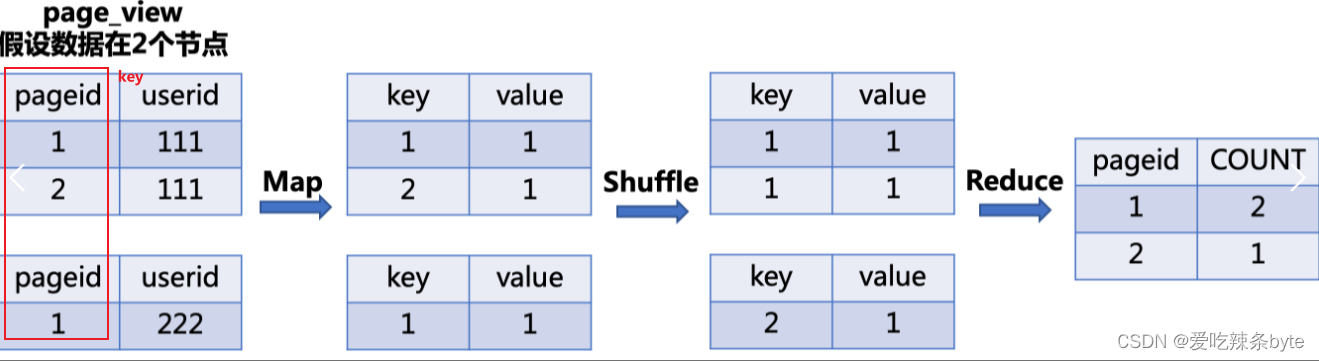
Hive SQL编译成MapReduce任务的过程
目录 一、架构及组件介绍 1.1 Hive底层架构 1.2 Hive组件 1.3 Hive与Hadoop交互过程 二、Hive SQL 编译成MR任务的流程 2.1 HQL转换为MR源码整体流程介绍 2.2 程序入口—CliDriver 2.3 HQL编译成MR任务的详细过程—Driver 2.3.1 将HQL语句转换成AST抽象语法树 词法、语…...

【C++】快速上手map、multimap、set、multiset
文章目录 一、前言二、set / multiset1. 常见应用2. 核心操作 三、map / multimap1. 常见应用2. 核心操作 一、前言 S T L STL STL 中的关联式容器分为树型结构和哈希结构,树型结构主要有四种: s e t set set、 m u l t i s e t multiset multiset、 m a…...
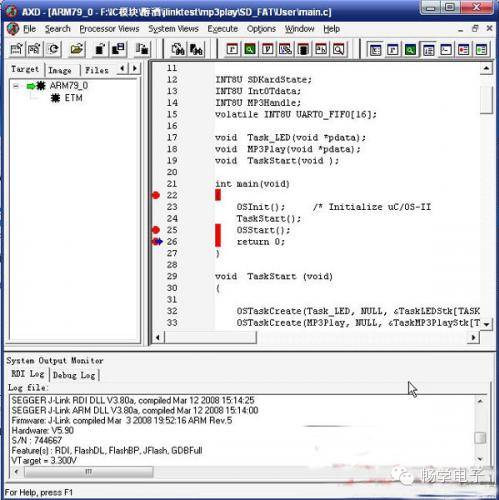
【分享】图解ADS+JLINK调试ARM
文章是对LPC2148而写的,但是对三星的44B0芯片同样适用,只需要在选择时将相应的CPU选择的S3C44B0就可以了。 JLINK在ADS下调试心得 前两天一个客户用jlink在ADS下调试LPC2148总报错,这个错误我之前在调试LPC2200的时候也碰到过,后…...
反无人机系统技术分析,无人机反制技术理论基础,无人机技术详解
近年来,经过大疆、parrot、3d robotics等公司不断的努力,具有强大功能的消费级无人机价格不断降低,操作简便性不断提高,无人机正快速地从尖端的军用设备转入大众市场,成为普通民众手中的玩具。 然而,随着消…...
Kotlin和Java 单例模式
Java 和Kotlin的单例模式其实很像,只是Kotlin一部分单例可以用对象类和委托lazy来实现 Java /*** 懒汉式,线程不安全*/ class Singleton {private static Singleton instance;private Singleton() {}public static Singleton getInstance() {if (insta…...
)
软考 系统分析师系列知识点之信息系统战略规划方法(9)
接前一篇文章:软考 系统分析师系列知识点之信息系统战略规划方法(8) 所属章节: 第7章. 企业信息化战略与实施 第4节. 信息系统战略规划方法 7.4.5 信息工程方法 信息工程(Information Engineering,IE&…...
政安晨:示例演绎TensorFlow的官方指南(一){基础知识}
为什么要示例演绎? 既然有了官方指南,咱们在官方指南上看看就可以了,为什么还要写示例演绎的文章呢? 其实对于初步了解TensorFlow的小伙伴们而言,示例演绎才是最重要的。 官方文档已经假定了您已经具备了相当合适的…...

node - 与数据库交互
在Web开发中,与数据库交互是常见的需求,用于持久化存储、检索和操作数据。不同的后端技术和数据库类型(如关系型数据库和非关系型数据库)有着不同的交互方式。下面介绍几种常见的数据库交互方法。 关系型数据库 关系型数据库(如MySQL、PostgreSQL、SQLite)使用结构化查…...

速盾:2024年cdn在5g时代重要吗
在2024年,随着5G技术的普及与应用,内容分发网络(Content Delivery Network,CDN)在数字化时代中的重要性将进一步巩固和扩大。CDN是一种用于快速、高效地分发网络内容的基础设施,它通过将内容部署在全球各地…...
微信小程序(四十一)wechat-http的使用
注释很详细,直接上代码 上一篇 新增内容: 1.模块下载 2.模块的使用 在终端输入npm install wechat-http 没有安装成功vue的先看之前的一篇 微信小程序(二十)Vant组件库的配置- 如果按以上的成功配置出现如下报错先输入以下语句 …...

所有设计模式大全及学习链接
文章目录 创建型设计模式结构型设计模式行为型设计模式 创建型设计模式 一种创建对象的设计模式,它们提供了一种灵活的方式来创建对象,同时隐藏了对象的创建细节。以下是常见的创建型设计模式: 工厂方法模式(Factory Method Patte…...
【Java程序设计】【C00264】基于Springboot的原创歌曲分享平台(有论文)
基于Springboot的原创歌曲分享平台(有论文) 项目简介项目获取开发环境项目技术运行截图 项目简介 这是一个基于Springboot的原创歌曲分享平台 本系统分为平台功能模块、管理员功能模块以及用户功能模块。 平台功能模块:在平台首页可以查看首…...

2024年,要特别注意这两个方位
家居风水对每个家庭都非常重要,可在无形中影响到人们的事业、财富以及健康运势。俗话说:“风水轮流转”,2024年为甲辰龙年,斗转星移、九宫飞星将改变宫位,新一年的磁场即将启动,方位的吉凶也会重新变动&…...
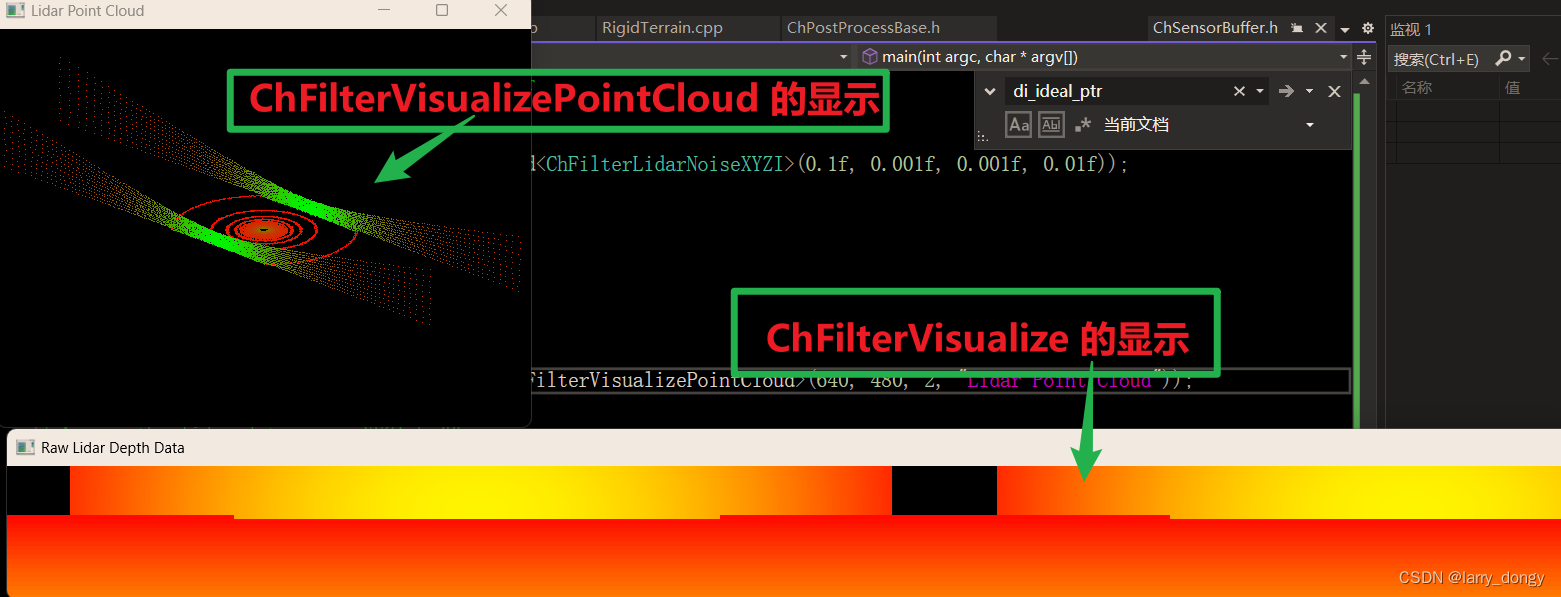
【Chrono Engine学习总结】5-sensor-5.1-sensor基础并创建一个lidar
由于Chrono的官方教程在一些细节方面解释的并不清楚,自己做了一些尝试,做学习总结。 1、Sensor模块 Sensor模块是附加模块,需要单独安装。参考:【Chrono Engine学习总结】1-安装配置与程序运行 Sensor Module Tutorial Sensor …...

springboot/ssm学生信息管理系统Java学生在线选课考试管理系统
springboot/ssm学生信息管理系统Java学生在线选课考试管理系统 开发语言:Java 框架:springboot(可改ssm) vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql 5.…...
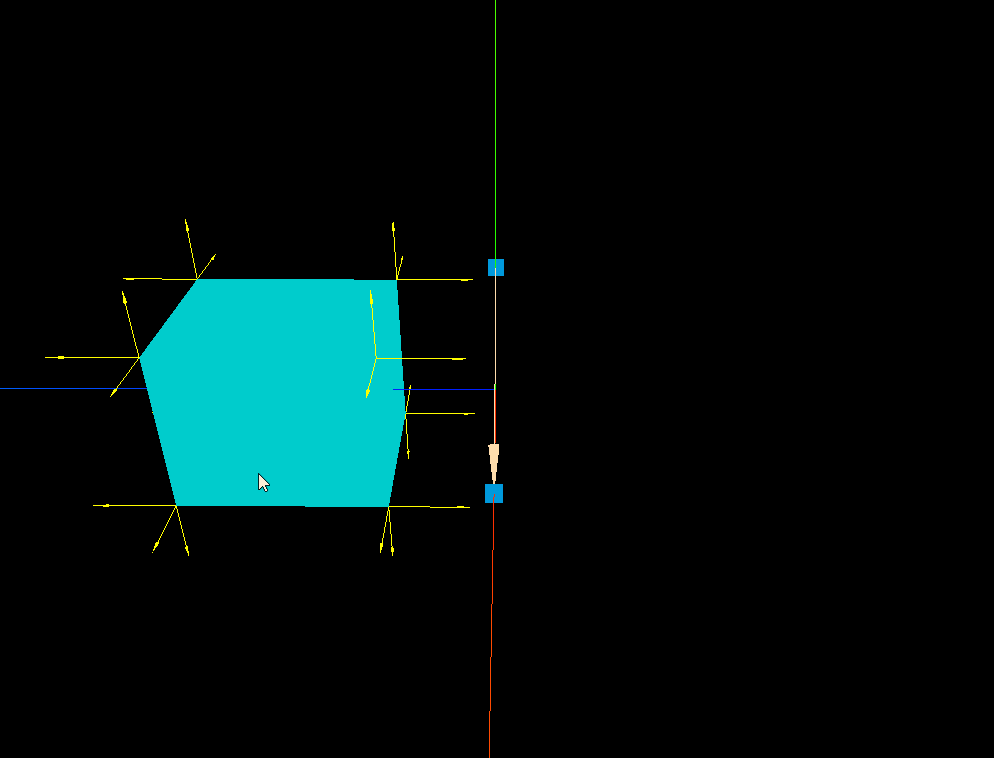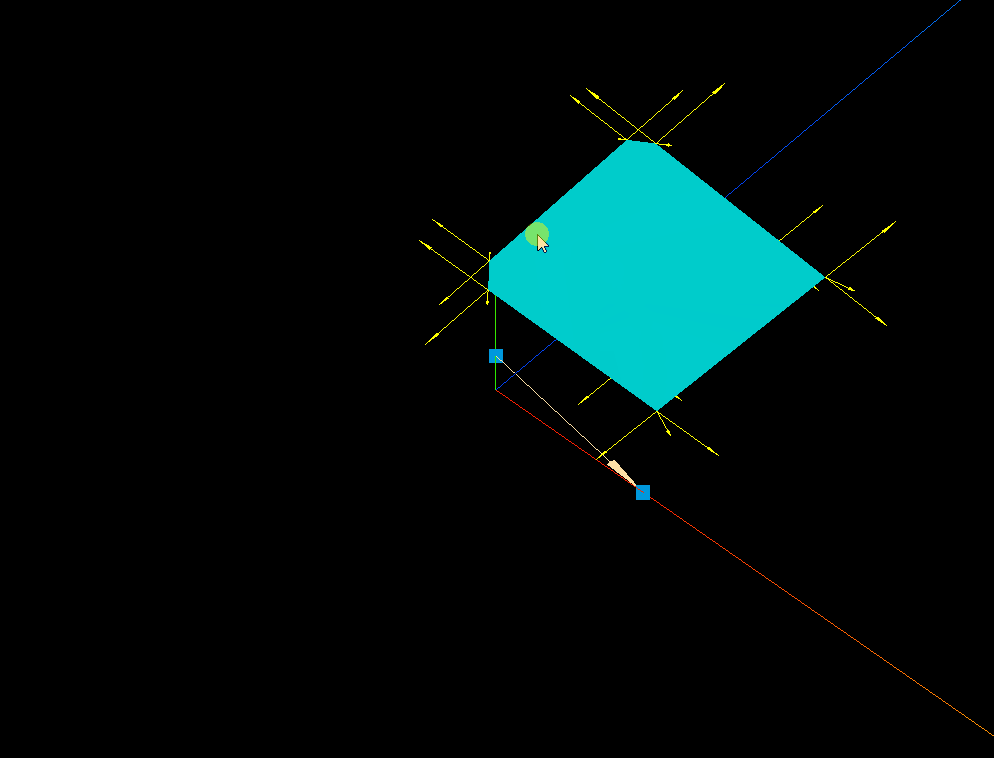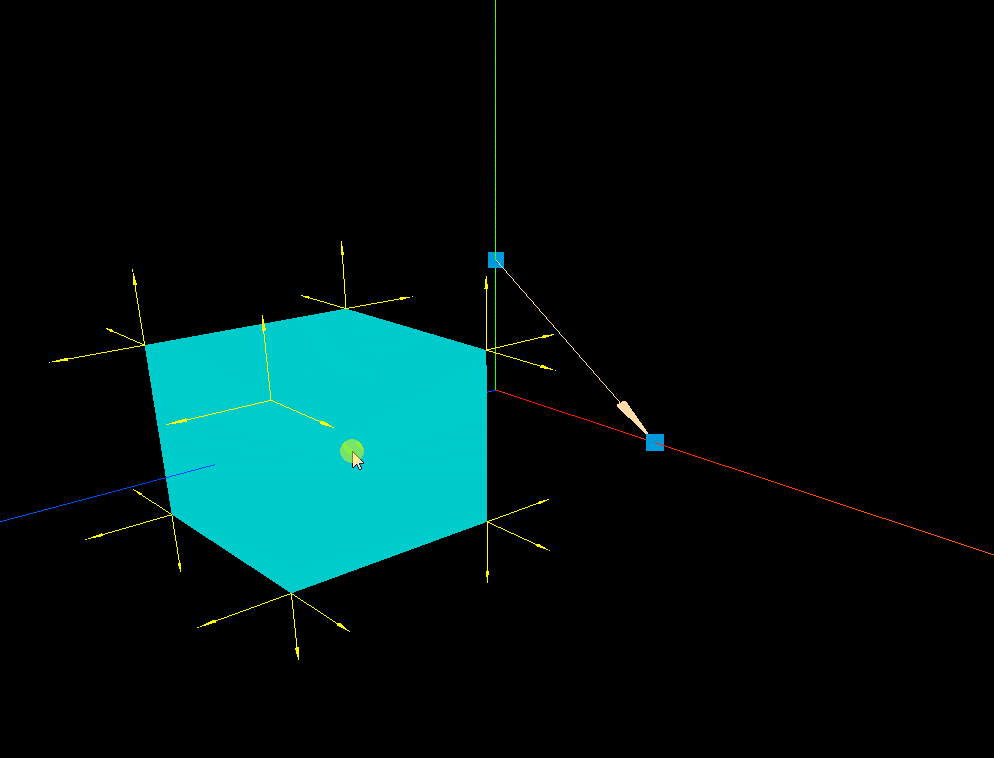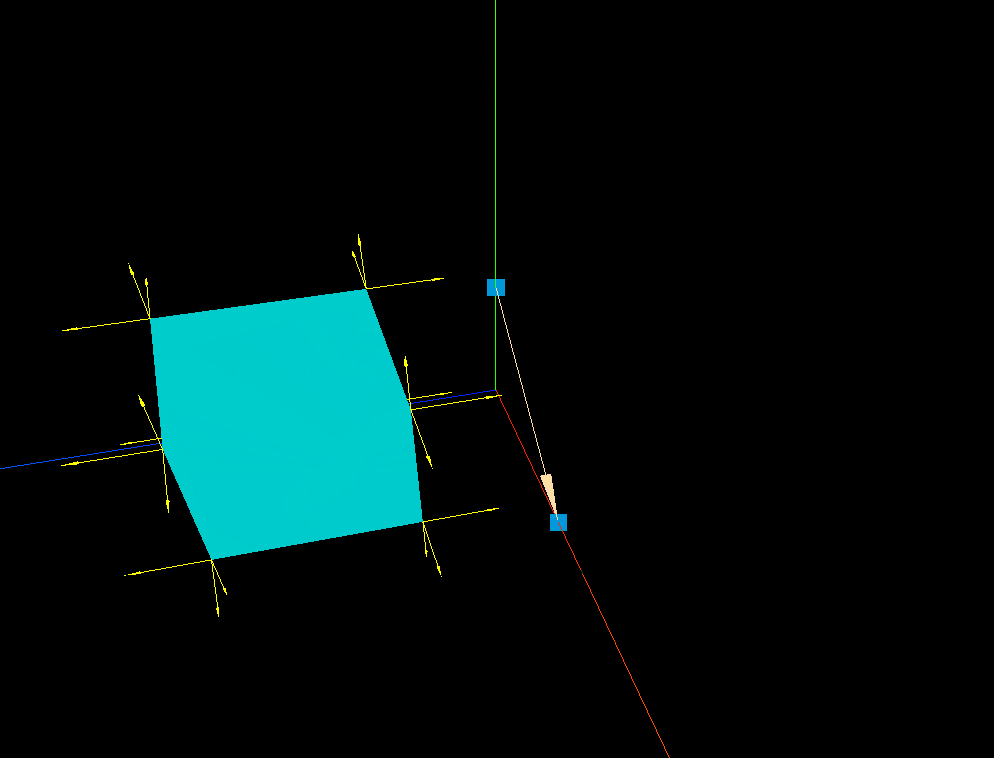
three.js 箭头ArrowHelper的实践应用
效果: 代码: <template><div><el-container><el-main><div class"box-card-left"><div id"threejs" style"border: 1px solid red"></div></div></el-main></…...

力扣hot2--哈希
推荐博客: for(auto i : v)遍历容器元素_for auto 遍历-CSDN博客 字母异位词都有一个特点:也就是对这个词排序之后结果会相同。所以将排序之后的string作为key,将排序之后能变成key的单词组vector<string>作为value。 class Solution …...
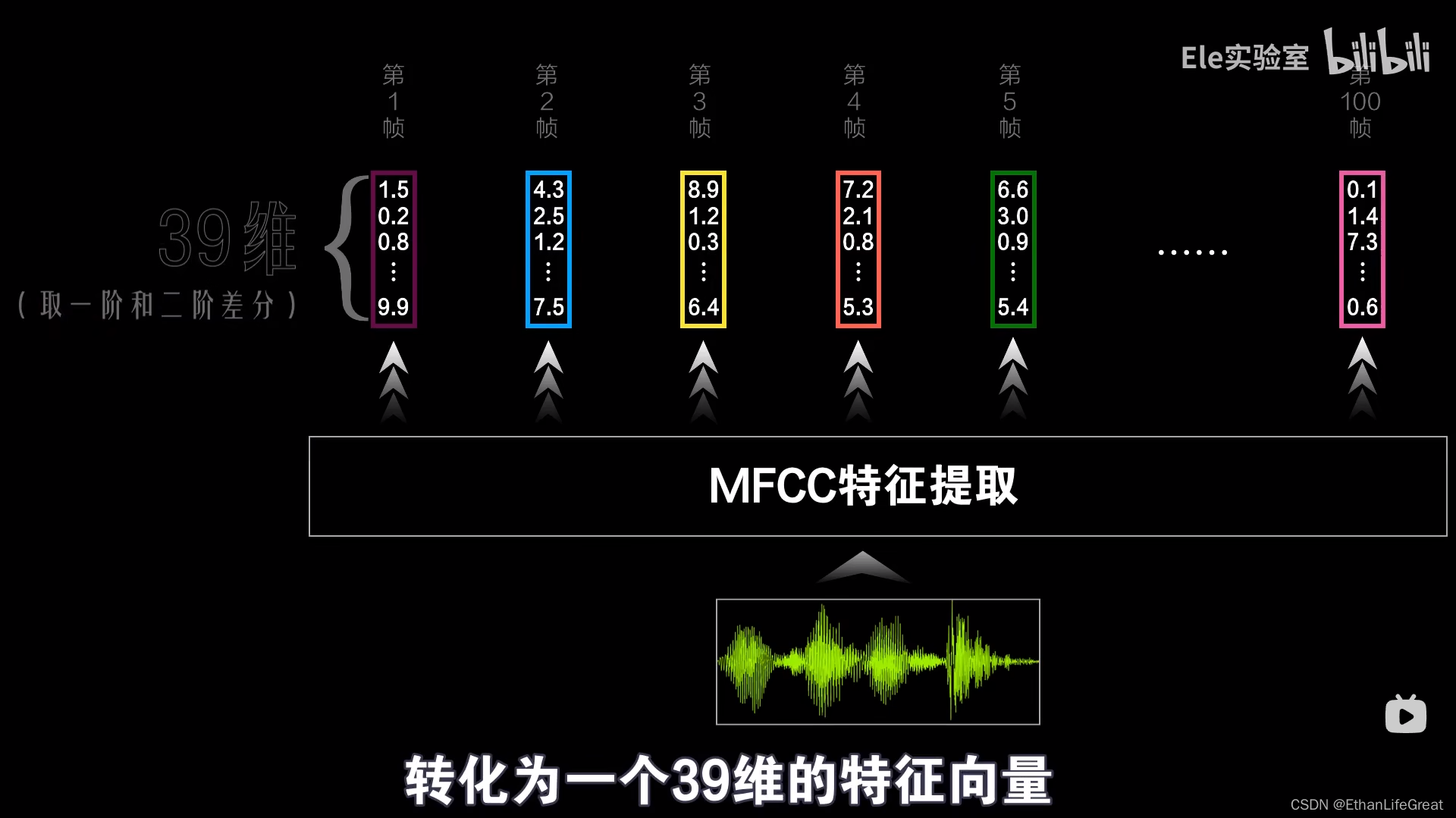
【正在更新】从零开始认识语音识别:DNN-HMM混合系统语音识别(ASR)原理
摘要 | Abstract 这是一篇对语音识别中的一种热门技术——DNN-HMM混合系统原理的透彻介绍。本文自2月10日开始撰写,计划一星期内写完。 1.前言 | Introduction 近期想深入了解语音识别(ASR)中隐马尔可夫模型(HMM)和深度神经网络-隐马尔可夫(DNN-HMM)混合模型&#…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...
