【小赛1】蓝桥杯双周赛第5场(小白)思路回顾
我的成绩:小白(5/6)
完稿时间:2024-2-13
比赛地址:https://www.lanqiao.cn/oj-contest/newbie-5/
相关资料:
1、出题人题解:“蓝桥杯双周赛·第5次强者挑战赛/小白入门赛”出题人题解 - 知乎 (zhihu.com)
2、矩阵快速幂:算法学习笔记(4):快速幂 - 知乎 (zhihu.com)
- 讲得挺好的,从快速幂到矩阵快速幂,以及在求解递推式中的应用。
3、矩阵乘法结合律证明:如何把矩阵乘法结合律的证明写得简单易懂(针对初学者) - 知乎 (zhihu.com)
- 我突然疑惑矩阵乘法为什么会满足结合律,找了篇文章,还没来得及看
文章目录
- 一、我思路回顾
- 1、十二生肖
- 2、欢迎参加福建省大学生程序设计竞赛
- 3、匹配二元组的数量
- 4、元素交换
- 5、下棋的贝贝
- 二、补题
- 6、方程
- 三、小结
- *脱节:从实践出发,又要从基础出发
- 回顾此回顾
一、我思路回顾
1、十二生肖
思路:
此题令我有点意外,显然2024是龙年,在12生肖中排第5个,print即可。
代码:
print(5)
2、欢迎参加福建省大学生程序设计竞赛
思路:
题中说将相同题数,相同罚时的队伍归为一类,那么如果每行输入作为一个元素,问题就变成了:有多少个不同的元素。而刚好集合数据结构就具有元素不重复的特点,将所有输入数据加入集合,输出集合中元素数量即可。
在python中,输入是字符串,将它作为字典的键就可实现去重。
代码:
if __name__ == '__main__':n = int(input())d = {}for i in range(n):x = input()if x not in d:d[x] = 1print(len(d))
3、匹配二元组的数量
思路:
这题想了一会儿,看到比值就想一项,但移完之后呢?
a i j = a j i \frac{a_i}{j}=\frac{a_j}{i} jai=iaj,变形一下, i a i = j a j ia_i=ja_j iai=jaj,于是可以将数组A的每一元素乘以它的下标,得新数组B,后统计B中重复元素数量。(注这里下标从1开始)
出现2次的算1一个匹配二元组,出现3次的算3个······出现x次的算组合数 C x 2 C^2_x Cx2,即 x ! 2 \frac{x!}{2} 2x!。
代码:
def f(x):'''x的阶乘'''r = 1for i in range(x):t = i + 1r *= t return rif __name__ == '__main__':n = int(input())nums = [int(x) for x in input().split(' ')]d = {}for i, num in enumerate(nums):nums[i] = (i + 1) * num for num in nums:if num not in d:d[num] = 0d[num] += 1result = 0for key in d:result += f(d[key]) // 2print(result)4、元素交换
思路:
这题像脑筋急转弯,初看非常的手足无措。
数组中有N个0和N个1,“不存在连续的0或1”,那合规数组仅两种:1)010101...,2)101010...,于是逐项对比输入与合规数组,得不同的项的数量c,而每次交换可以把两个不同项变为相同,所以交换次数为n/2 。
那为什么,每次交换可以减少两个不同?
因为1对上0的数量,必然和0对上1的数量一样。不妨令N为5,假设合规数组中,有3个1没匹配上。那么必然有2个1匹配上了,那么输入中还剩3个1,让合规数组中的0也有3个匹配不上。
合规:0 1 0 1 0 1 0 1 0 1
输入: 0 0 0 1 1
在比赛中,我经常就只能先将输入胡乱摆弄一阵,然后去猜规律,有时猜得对,有时猜得半对,有时猜得不对。在下一题,下棋的贝贝中,就是先草率地猜错了,然后又重新猜。
代码:
def jdz(x):'''绝对值'''return x if x >= 0 else -xif __name__ == '__main__':n = int(input())nums = [int(x) for x in input().split(' ')]# 合规数组h1 = [0, 1] * n h2 = [1, 0] * n# 对比差距c1 = sum([jdz(h1[i] - nums[i]) for i in range(len(nums))])c2 = sum([jdz(h2[i] - nums[i]) for i in range(len(nums))])c = min(c1, c2)r = c // 2 # 每次交换可以减少两个不同print(r)
5、下棋的贝贝
思路:
题意还比较清晰,在整数格子上放棋子,横竖挨着的棋子算相邻,相邻的棋子有一条边,如果边的总数为e,输出 2 ∗ e 2*e 2∗e 。
于是我开始在草稿纸上施法,期待老天爷降下神谕。很快我就觉得,这是一个类似等差的数列,之后隔两项的差都是3。然而提交之后的error告诉我,还是高兴得太早了。
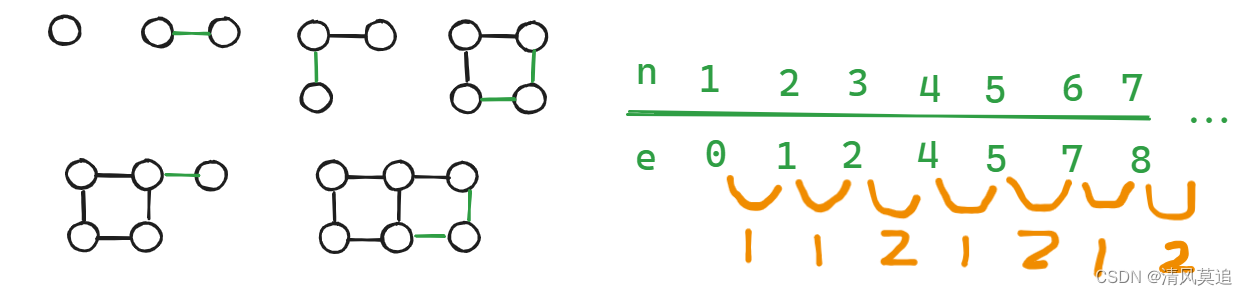
于是我又猜了第二版。有的棋子放下时不增加边(1号)或只会增加一条边,如下图中带圈圈的;有的棋子放下时增加两条边,如下图中不带圈圈的。然后统计带圈圈类型的棋子数量。
设总棋子数为m,平方根向下取整为n,于是带圈圈的棋子数single_edge分两类统计:
- 一个是内侧正方形中的(如图中蓝框),数量为2n-1
- 外正方形的,会有两个临界值,当m的值超过它们时,带圈圈的棋子数加1。
如果每个棋子会产生两条边,那么总边数为 2 m 2m 2m。然后减去只产生一条边的棋子数量(因为一号棋子不产生边,可以抵两个只产生一条边的棋子),就可以得到边的总数。
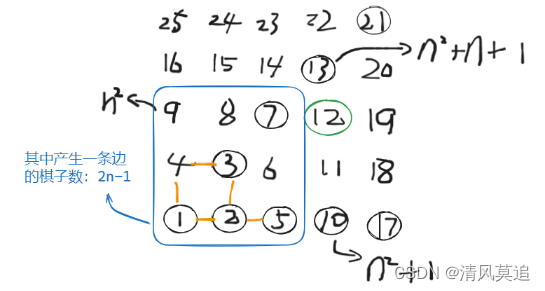
为什么以上方法就是放置棋子的最佳策略(产生最多的边)?
大家可以思考一下。
代码:
import mathdef method2(m):'''边的数量'''n = math.sqrt(m)n = math.floor(n)single_edge = n * 2if m >= n**2 + 1:single_edge += 1if m >= n**2 + 1 + n:single_edge += 1 r = 2 * m - single_edgereturn rif __name__ == '__main__':m = int(input())r = method2(m)print(r * 2)
二、补题
6、方程
这题当时完全没有思路,希望我下次会有进步。如果还没有,就多下几次!
思路:
有两个步骤。第一步是得到递推式,但n数据范围是 [ 1 , 1 0 9 ] [1,10^9] [1,109],逐步递推时间复杂度 O ( n ) O(n) O(n)太高。于是第二步用到矩阵快速幂,将复杂度降到 O ( l o g n ) O(logn) O(logn)。
1、得到递推式
题为 x + 1 x = k x+\frac{1}{x}=k x+x1=k,求 x n + 1 x n x^n+\frac{1}{x^n} xn+xn1的值。令 f ( n ) = x n + 1 x n f(n)=x^n+\frac{1}{x^n} f(n)=xn+xn1,则: k f ( n ) = ( x + 1 x ) ( x n + 1 x n ) = f ( n + 1 ) + f ( n − 1 ) kf(n)=(x+\frac{1}{x})(x^n+\frac{1}{x^n})=f(n+1)+f(n-1) kf(n)=(x+x1)(xn+xn1)=f(n+1)+f(n−1)。
即: f ( n + 1 ) = k f ( n ) − f ( n − 1 ) f(n+1)=kf(n)-f(n-1) f(n+1)=kf(n)−f(n−1)
又易得: f ( 0 ) = 2 f(0)=2 f(0)=2, f ( 1 ) = k f(1)=k f(1)=k 。
2、矩阵快速幂
这部分参考了文首的资料1和资料2,大家也可以看一下。
a、为什么要有快速幂算法?
在求一个数的n次幂的过程中,比如 1 0 8 = 10 ∗ 10 ∗ 10 ∗ 10 ∗ 10 ∗ 10 ∗ 10 ∗ 10 10^8=10*10*10*10*10*10*10*10 108=10∗10∗10∗10∗10∗10∗10∗10,需要8次乘法运算。但如果这样算: 1 0 2 = 10 ∗ 10 , 1 0 4 = 1 0 2 ∗ 1 0 2 , 1 0 8 = 1 0 4 ∗ 1 0 4 10^2=10*10,10^4=10^2*10^2,10^8=10^4*10^4 102=10∗10,104=102∗102,108=104∗104,只需要3次乘法,这其实是二分的思路。
也就是说,可以以 O ( l o g n ) O(logn) O(logn)的时间复杂度计算数x的n次幂 x n x^n xn。
b、矩阵乘法如何计算递推式?
就以本题为例,我们发现 [ k − 1 1 0 ] [ f n − 1 f n − 2 ] = [ f n f n − 1 ] \begin{bmatrix}k & -1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix}f_{n-1}\\f_{n-2} \end{bmatrix} = \begin{bmatrix}f_{n}\\f_{n-1} \end{bmatrix} [k1−10][fn−1fn−2]=[fnfn−1] ,于是我们每一次矩阵乘法,就是一步递推。
但这有什么用呢,好像莫名奇妙凑出一个矩阵的形式,把简单的问题复杂化。
c、快速幂加上矩阵乘法:快速计算递推式。
令 A = [ k − 1 1 0 ] A=\begin{bmatrix}k & -1 \\ 1 & 0 \end{bmatrix} A=[k1−10] ,则: [ f n f n − 1 ] = A [ f n − 1 f n − 2 ] = A 2 [ f n − 2 f n − 3 ] = . . . = A n − 1 [ f 1 f 0 ] \begin{bmatrix}f_{n}\\f_{n-1} \end{bmatrix} = A \begin{bmatrix}f_{n-1}\\f_{n-2} \end{bmatrix} = A^2 \begin{bmatrix}f_{n-2}\\f_{n-3} \end{bmatrix} = ... = A^{n-1} \begin{bmatrix}f_{1}\\f_{0} \end{bmatrix} [fnfn−1]=A[fn−1fn−2]=A2[fn−2fn−3]=...=An−1[f1f0],
看见 A A A头上的幂次了吗?将递推的时间复杂度从 O ( n ) O(n) O(n)降到 O ( l o g n ) O(logn) O(logn),我想你已经知道该怎么做了。
代码:
class Matrix:'''封装矩阵乘法'''MOD_NUM = 10**9 + 7def __init__(self, value) -> None:self.v: list = value def mul(self, obj):# 两个矩阵维度分别是(a,b), (b,c)obj: Matrix = obja, b, c = len(self.v), len(self.v[0]), len(obj.v[0])matrix = [[0] * c for i in range(a)] # 乘积维度:(a,c)r = Matrix(matrix)for i in range(a):for j in range(c):for k in range(b):r.v[i][j] = (r.v[i][j] + self.v[i][k] * obj.v[k][j]) % self.MOD_NUMreturn rdef mi(A: Matrix, n: int) -> Matrix:'''求矩阵A的n次幂'''if n == 1:return Aif n % 2 == 1:return mi(A, n-1).mul(A)else:t = mi(A, n // 2)return t.mul(t)def method(n, k):'''求解一个测试用例'''if n == 1:return k elif n > 1:A = Matrix([[k, -1], [1, 0]])F = Matrix([[k], [2]]) # f(0)=2, f(1)=kR = mi(A, n-1).mul(F)return R.v[0][0]if __name__ == '__main__':m = int(input())for _ in range(m):n, k = map(int, input().split(' ')) # 以前我总用列表推导式print(method(n, k))这次比赛强者级还有3个题,但比赛就没看,相关内容也没咋学,又考虑到时间问题,就不打算补了。
三、小结
本次比赛有小白和强者两个级别,感觉自己还比较菜,于是报了小白。后来发现小白的后3题正是强者级的头三题,这么看来,我在强者级只能写两个题?但问题不大,我对未来仍然抱有一种迷之信心。
*脱节:从实践出发,又要从基础出发
脱节问题在我们的生活中尤其严重。常有人说大学教育与社会需求脱节。然而细看我自己,又何尝不是处处脱节?就如学英语数十年,却不能说英语,学习和运用是脱节的。读英文时脑海里止步于模糊的“英式汉语”,想将心中的地道汉语用英语说出来,自然是困难的,因为缺少了一个从输入英语到地道汉语的过程。盲目期待所谓“英语思维”,于是学习方法本身便是脱节的。汉语是我们的母语,想将它一下子甩掉不太现实。
早在学校的数据结构与算法课程,弊端就已经显现。算法本身被孤立地灌输给我,要我如何能够面对问题分析问题用算法解决问题?大多的算法都只是跟着实现一遍,也大概就算是学过了。诚然,师傅领进门,修行靠个人,学习本就要靠自己的努力。可我就是缺少指导呀。(吐槽)
回看算法的学习,也应该多参加小比赛,多自己写,才能学会自己写。实践中有其独特而珍贵的经验,而且能为学习方向的调整提供指导。
然而,也常听见一个建议:在做的过程中学。但我曾理解得有些片面,于是钟爱教程而疏于理论,止于模仿而失了变通;于是遇到难题抓脑袋,有一段时间,沉陷在反复的焦虑之中。后来有一次zxl对我说,解决不了,就要想想是不是缺了基础知识,又让我一下子觉得:早该这样。
再看算法学习,总专注于比赛、刷题,而不重视系统性的理论学习,同样不合适。望自警醒。
拼命追着跑还是被匆匆拖着跑,都不太好,得一起跑。
回顾此回顾
要常回顾,以免在歧途上发足狂奔。但我目前有一个大问题,就是我太慢了,相当于在路上花费了太多的时间东张西望。此次比赛回顾,写到这句话,我已经花了8小时。比赛本身也才2小时!
这种习惯对于“常回顾”的目标,必然是极大的负担。
相关文章:

【小赛1】蓝桥杯双周赛第5场(小白)思路回顾
我的成绩:小白(5/6) 完稿时间:2024-2-13 比赛地址:https://www.lanqiao.cn/oj-contest/newbie-5/ 相关资料: 1、出题人题解:“蓝桥杯双周赛第5次强者挑战赛/小白入门赛”出题人题解 - 知乎 (zhihu.com) 2、矩阵快速幂&…...
-yum二进制部署)
docker (二)-yum二进制部署
yum安装docker(Linux) 安装环境:CentOS 7.9 一 如果之前安装了旧版docker,请先删除 sudo yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotat…...
)
【深度学习】S2 数学基础 P2 线性代数(下)
目录 范数的意义范数的数学意义范数之于深度学习的意义 L1 范数与 L2 范数L1 范数L2 范数 小结 本节博文是线性代数第二部分,主要内容为 L 1 L1 L1 范数与 L 2 L2 L2 范数;有关线性代数基础知识,请访问:【深度学习】S2 数学基础…...

【软考高级信息系统项目管理师--考试内容大纲篇】
🚀 作者 :“码上有前” 🚀 文章简介 :软考高级–信息系统项目管理师 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬 软考高级信息系统项目管理师--考试内容大纲篇 1.信息化发展2.信息技术发展3.信息系…...

C语言——枚举类型
📝前言: 在之前的文章中我们已经讲解了自定义类型中的结构体类型和联合体类型,现在我们再充分学习一下C语言中的枚举类型: 1,什么是枚举类型 2,枚举类型的定义和变量的声明 3,对变量进行赋值 &a…...

linux---内存管理
一 虚拟内存 即使是现代操作系统中,内存依然是计算机中很宝贵的资源,看看你电脑几个T固态硬盘,再看看内存大小就知道了。 为了充分利用和管理系统内存资源,Linux采用虚拟内存管理技术,利用虚拟内存技术让每个进程都有…...

v-model原理
v-model原理 v-model原理表单类组件封装v-model简化代码 v-model原理 1.原理: v-model本质上是一个语法糖。例如应用在输入框上,就是value属性 和 input 事件的合写 <template><div id"app" ><input v-model"msg"…...
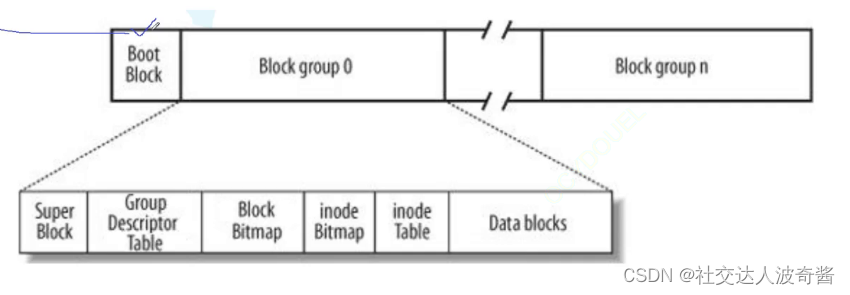
波奇学Linux:文件系统
磁盘认识 磁盘被访问的基本单元是扇区-512字节。 磁盘可以看成多个同心圆,每个同心圆叫做磁道,多个扇区组成同心圆。 我们可以把磁盘看做由无数个扇区构成的存储介质。 要把数据存到磁盘,先定位扇区,用哪一个磁头,…...

项目访问量激增该如何应对
✨✨ 欢迎大家来到喔的嘛呀的博客✨✨ 🎈🎈希望这篇博客对大家能有帮助🎈🎈 目录 引言 一. 优化数据库 1.1 索引优化 1.2 查询优化 1.3 数据库设计优化 1.4 事务优化 1.5 硬件优化 1.6 数据库配置优化 二. 增加服务器资源…...

【Linux环境基础开发工具的使用(yum、vim、gcc、g++、gdb、make/Makefile)】
Linux环境基础开发工具的使用yum、vim、gcc、g、gdb、make/Makefile Linux软件包管理器- yumLinux下安装软件的方式认识yum查找软件包安装软件如何实现本地机器和云服务器之间的文件互传卸载软件 Linux编辑器 - vimvim的基本概念vim下各模式的切换vim命令模式各命令汇总vim底行…...
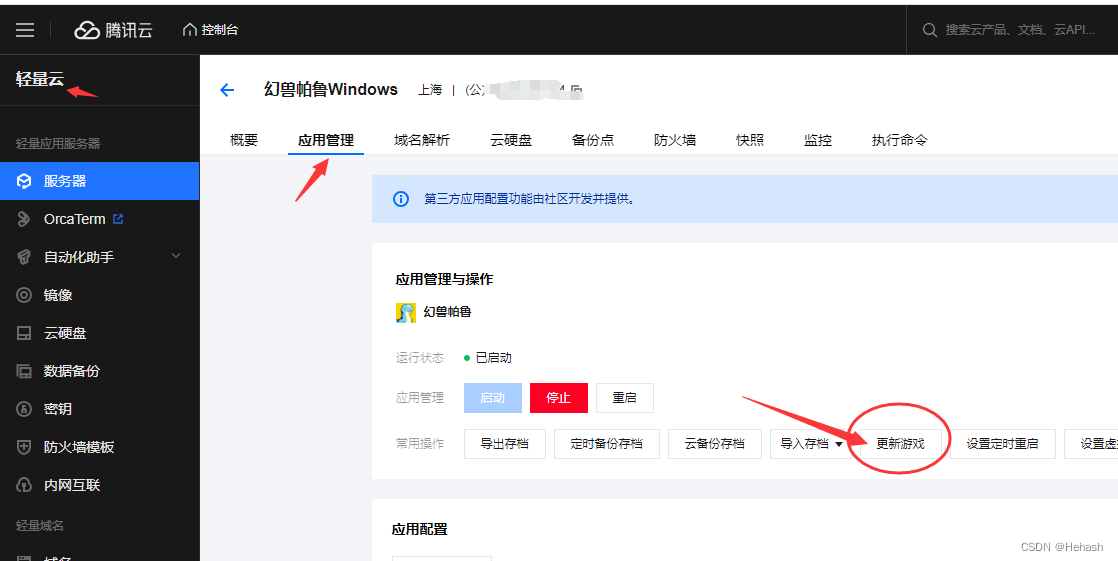
幻兽帕鲁官方更新了,服务器端怎么更新?
幻兽帕鲁官方客户端更新了,那么它的服务器端版本也是需要更新的,不然版本不一致的话,就不能进入游戏了。 具体的更新方法有两种,一是手动输入命令进行更新。第二种是在面板一键更新。 无论你是在阿里云或者腾讯云购买的一键部署…...

axios-retry 响应异常
最近项目中遇到 axios 异步请求异常中断, 错误码为 “ECONNABORTED” 奇怪的是排查前端代码并没有发现有主动调用 abort 取消请求的 由于为何网络请求失败的原因找不到, 但是重试请求就是成功的, 所以计划使用 axios-retry 在网络错误时重新请求 import axiosRetry from axios…...
Vue项目创建和nodejs使用
Vue项目创建和nodejs使用 一、环境准备1.1.安装 node.js【下载历史版本node-v14.21.3-x64】1.2.安装1.3.检查是否安装成功:1.4.在Node下新建两个文件夹 node_global和node_cache并设置权限1.5.配置npm在安装全局模块时的路径和缓存cache的路径1.6.配置系统变量&…...

【机器学习案例3】从科学论文图片中提取标题、作者和摘要【含源码】
在这个项目中,我的目标是从科学论文图片中提取某些部分(标题、作者和摘要)。预期提取部分是科学论文中常见的部分,例如标题、摘要和作者。输入与最终结果。我的输入是将第一页纸转换成图像。最终结果是一个 txt 文件,其中包含标题、作者和摘要部分,如下图1和图2所示。我将…...

【开源】JAVA+Vue.js实现天然气工程运维系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 系统角色分类2.2 核心功能2.2.1 流程 12.2.2 流程 22.3 各角色功能2.3.1 系统管理员功能2.3.2 用户服务部功能2.3.3 分公司(施工单位)功能2.3.3.1 技术员角色功能2.3.3.2 材料员角色功能 2.3.4 安…...

什么是智慧隧道,如何建设智慧隧道
一、隧道管理的难点痛点 近年来隧道建设规模不断扩大,作为隧道通车里程最多、规模最大的国家,截至2022年底,我国公路隧道共有24850处、2678.43万延米,其中特长隧道1752处、795.11万延米,长隧道6715处、1172.82万延米。…...

jupyter notebook
输入jupyter notebook 停止运行就用ctrlc 全部注释先全选 ,在按ctrl/...

MongoDB聚合:$listSearchIndexes
$listSearchIndexes返回指定集合现有Atlas Search索引的信息。 **重要:**该命令只能在托管的MongoDB Allas,并且要求群集层级至少为M10。 语法 db.<collection>.aggregate([{$listSearchIndexes:{id: <indexId>,name: <indexName>}…...
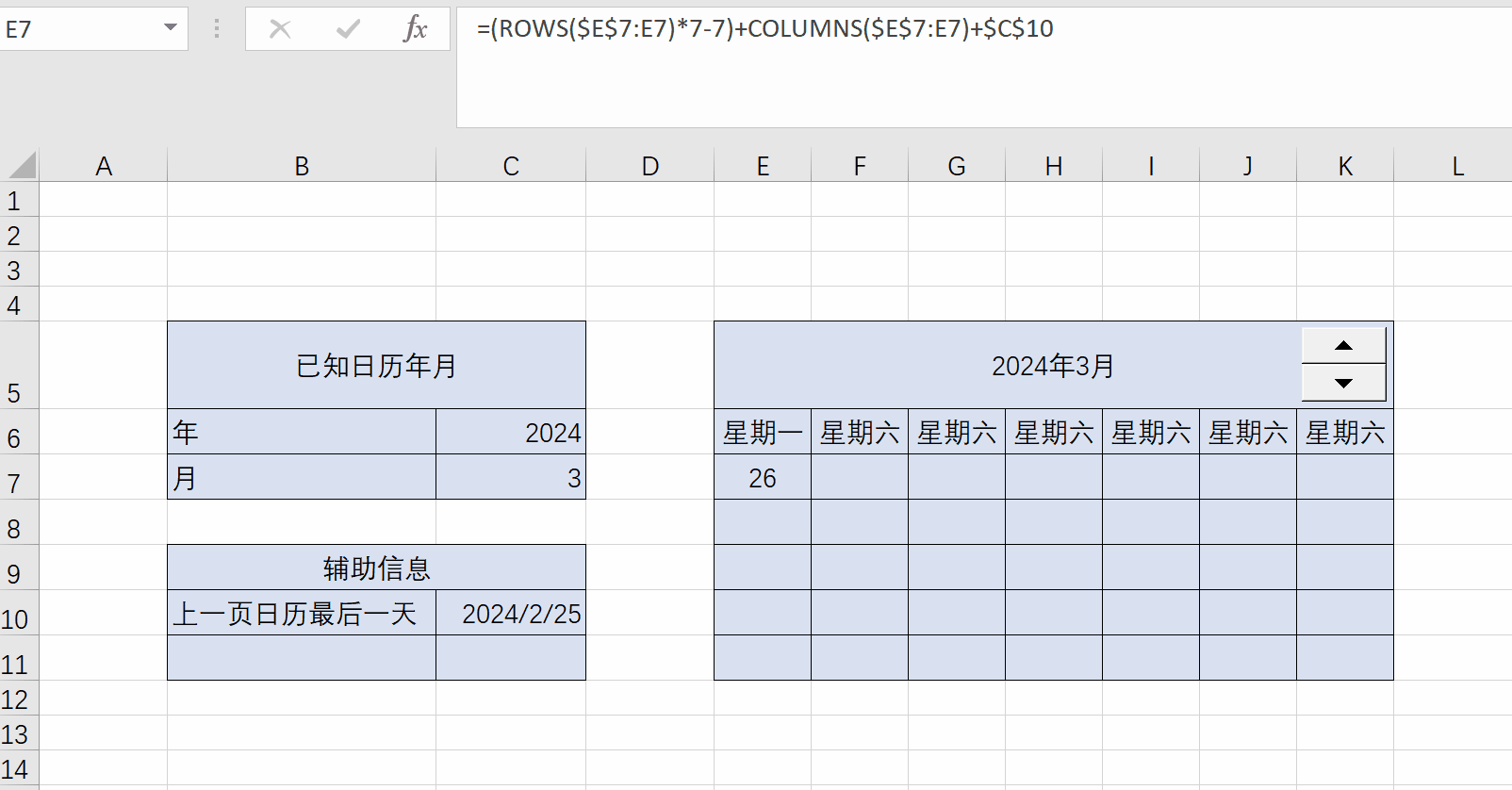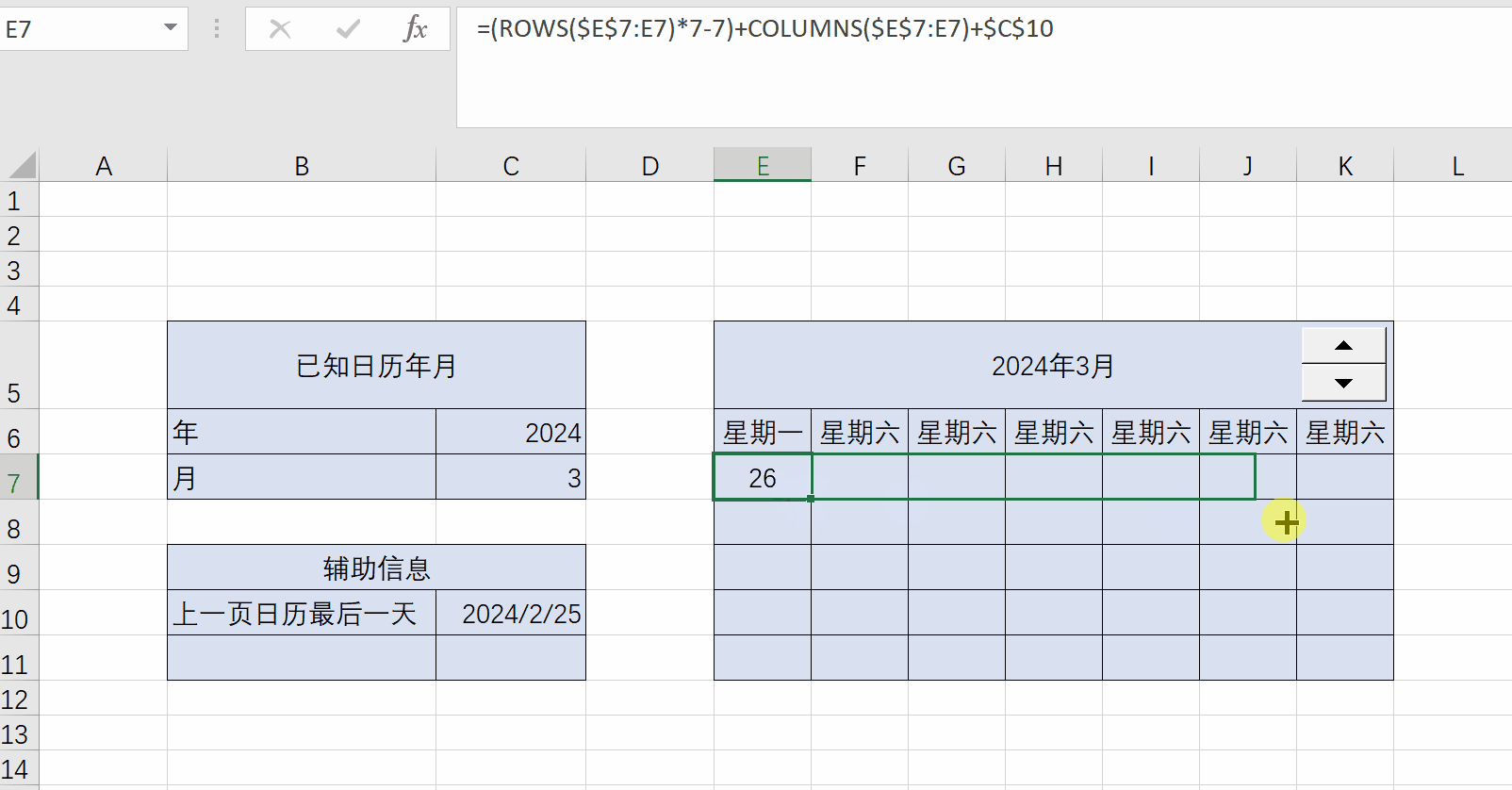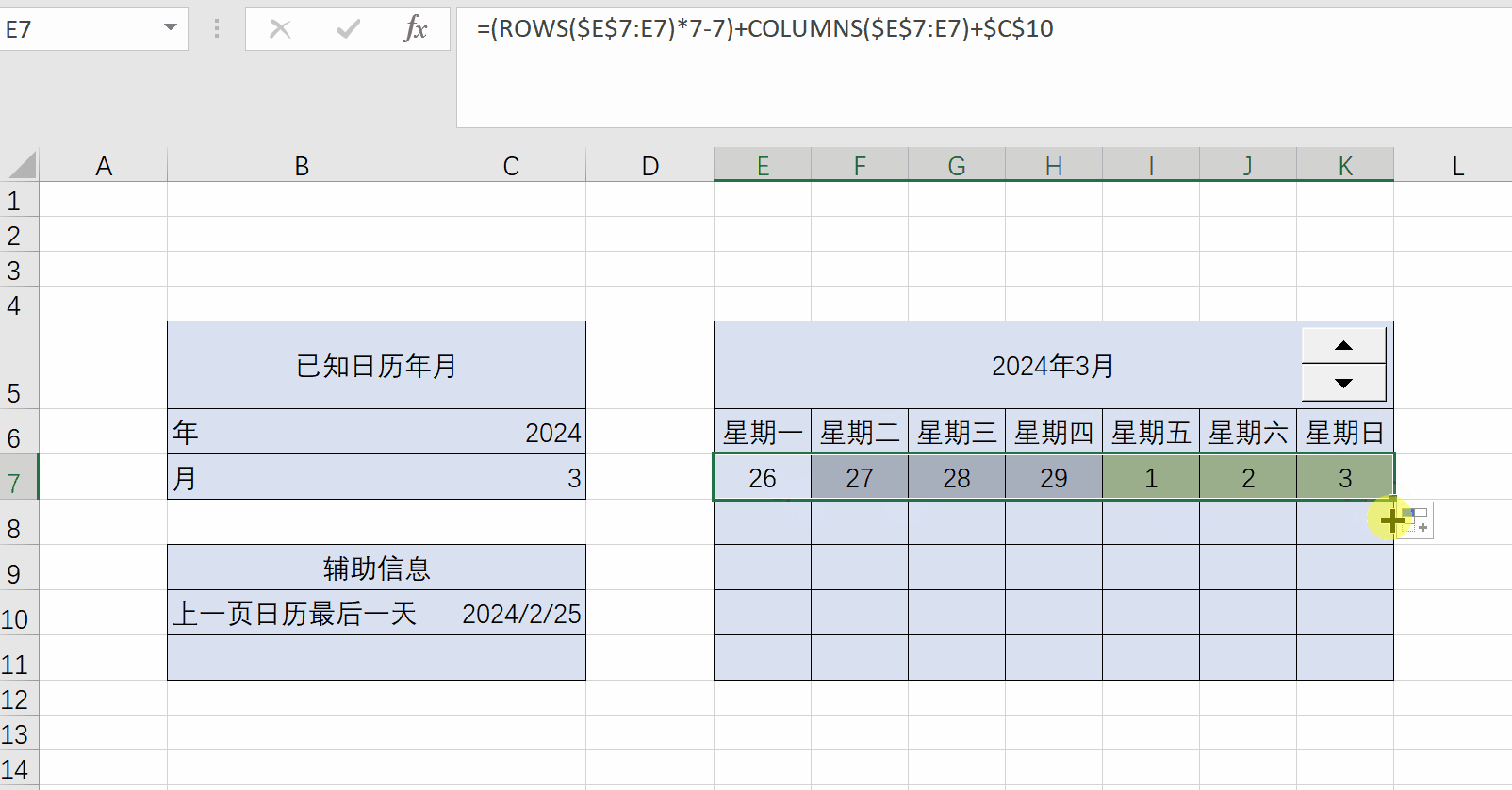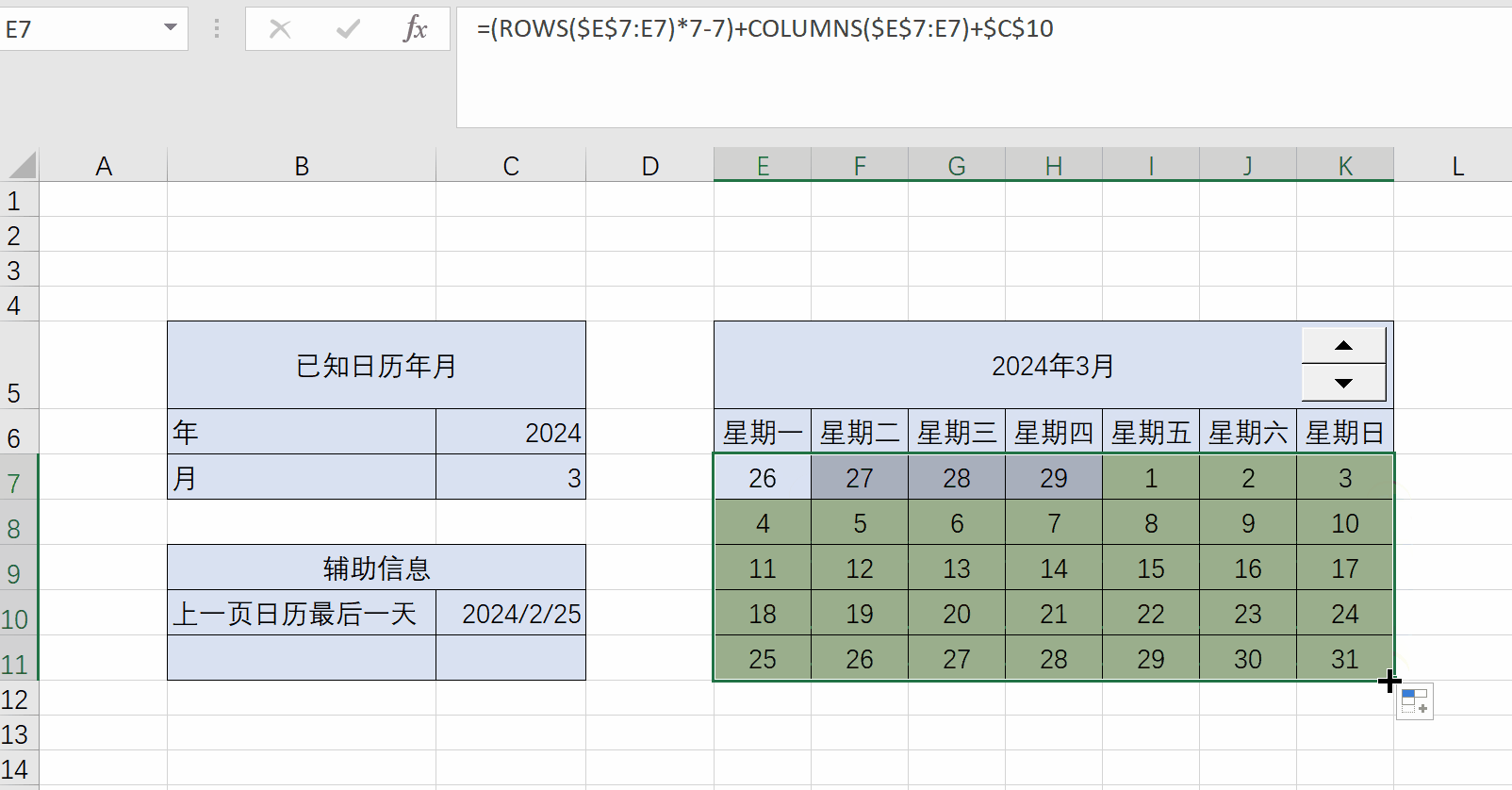
Excel练习:日历
Excel练习:日历 题目:制作日历 用rows和columns函数计算日期单元格偏移量 一个公式填充所有日期单元格 ...

【C语言】指针练习篇(上),深入理解指针---指针和数组练习题和sizeof,strlen的对比【图文讲解,详细解答】
欢迎来CILMY23的博客喔,本期系列为【C语言】指针练习篇(上),深入理解指针---指针数组练习题和sizeof,strlen的对比【图文讲解,详细解答】,图文讲解指针和数组练习题,带大家更深刻理解指针的应用…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...
