MATLAB | 情人节画个花瓣venn图?
之前七夕节情人节各种花,相册,爱心啥的都快画够了,今年画个花瓣韦恩图?
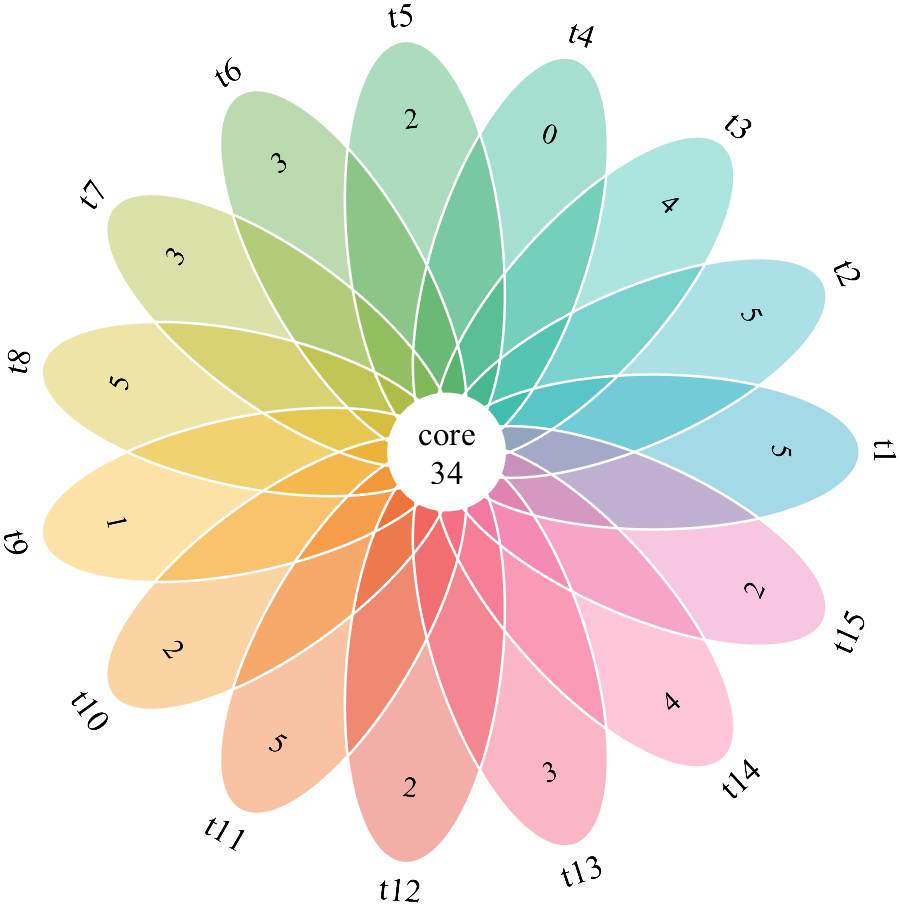

花瓣上的数字是仅属于该类的样本数,而中心的数字是属于每一类的样本数
教程部分
0 数据准备
% 给组起名t1 t2 t3...t15
setName = compose('t%d', 1:15);% 随机生成数据
Data = [rand(200, 15) > .1; rand(200, 15) > .85];% 设置字体
numFont = {'FontSize', 14, 'FontName', 'Times New Roman'};
labFont = {'FontSize', 16, 'FontName', 'Times New Roman'};
其中Data数据是个0-1矩阵,矩阵每一行代表一个样本,如果第n列是1代表该样本属于第n类,是0则代表不属于。
1 配色
CList = lines(15);
% C = flowerPlotColor();
% CList = C.CList631;
这里直接取MATLAB自带的lines配色,当然我也准备了很多其他配色,可以复制下来用:
function C=flowerPlotColor
C.CList1877 = [0.2431 0.3294 0.58820.5098 0.5647 0.73330 0.5569 0.80780.3490 0.7804 0.92160.0275 0.4431 0.52940.4157 0.6667 0.71760.0392 0.5647 0.52550.3294 0.7490 0.71760.5569 0.1255 0.26270.7373 0.4784 0.56080.8784 0.3765 0.49410.9255 0.6275 0.69800.9961 0.6275 0.56470.9961 0.8118 0.78040.7216 0.7373 0.75690.8824 0.8863 0.8980];
C.CList1514 = [0.4078 0.5647 0.81570.9098 0.7843 0.65880.9725 0.8784 0.72160.9725 0.9725 0.97250.2196 0.3137 0.43920.5333 0.6588 0.97250 0 00.5961 0.5961 0.69020.3451 0.4706 0.56470.8471 0.8471 0.97250.7216 0.7216 0.81570.8157 0.6902 0.56470.7216 0.5961 0.47060.2510 0.4078 0.62750.7216 0.7843 0.9725];
C.CList1596 = [0.2549 0.5490 0.94120.9882 0.7059 0.25490.8784 0.2510 0.03920.0196 0.3922 0.57250.7490 0.7490 0.74900.1020 0.2314 0.41181.0000 0.8902 0.50980.0706 0.6118 0.86670.7922 0.4196 0.29410 0.3608 0.85880.9529 0.8235 0.53330.3137 0.3882 0.50590.9451 0.7255 0.65880.8784 0.5137 0.03920.4706 0.5765 0.7451];
C.CList1470 = [0.1882 0.4078 0.59610.2824 0.5020 0.69020.9098 0.8157 0.62750.7843 0.6902 0.50200.3765 0.5961 0.78430.1255 0.1882 0.28240 0 00.4078 0.3765 0.28240.5961 0.5333 0.37650.5647 0.7529 0.90980.2196 0.3137 0.47060.6902 0.7216 0.75290.9725 0.9725 0.97250.5020 0.5333 0.59610.9725 0.9098 0.7843];
C.CList1827 = [1.0000 0.6118 00.9686 0.7412 0.35291.0000 0.8000 0.60001.0000 1.0000 0.20001.0000 1.0000 0.61180.8039 0.3882 0.38820.8000 0.6000 0.80001.0000 0.6196 0.38820.3922 0.4275 0.80000.6118 0.6118 1.00000.2000 0.6000 1.00000.6000 0.8000 1.00001.0000 1.0000 0.80000.6941 0.5843 0.47840.9294 0.5333 0.29800.9608 0.9294 00.8667 1.0000 1.0000];
C.CList1607 = [0.8863 0.5686 0.56860.6000 0.8667 0.57250.5765 0.8471 0.72550.5804 0.7686 0.82750.5804 0.6039 0.80780.7020 0.5804 0.80000.8000 0.5882 0.69410.8000 0.6431 0.60000.8745 0.8980 0.57251.0000 0.6471 0.37650.4196 1.0000 0.38820.3961 1.0000 0.80000.3961 0.7686 1.00000.3961 0.4196 1.00000.6784 0.3961 1.00001.0000 0.3961 0.95691.0000 0.3961 0.51761.0000 0.3961 0.3961];
C.CList631 = [0.1059 0.6392 0.77650.1725 0.7098 0.75290.1882 0.7373 0.67840.1294 0.6902 0.52940.2000 0.6510 0.36080.3412 0.6392 0.21570.6353 0.7137 0.15290.8353 0.7333 0.12940.9725 0.7137 0.12550.9725 0.5725 0.09020.9412 0.4039 0.09800.8784 0.2039 0.14900.9647 0.2863 0.44310.9882 0.4431 0.61960.9216 0.4510 0.70200.8078 0.4118 0.74510.6353 0.4275 0.76080.4706 0.4510 0.75290.3098 0.4863 0.7294];
end
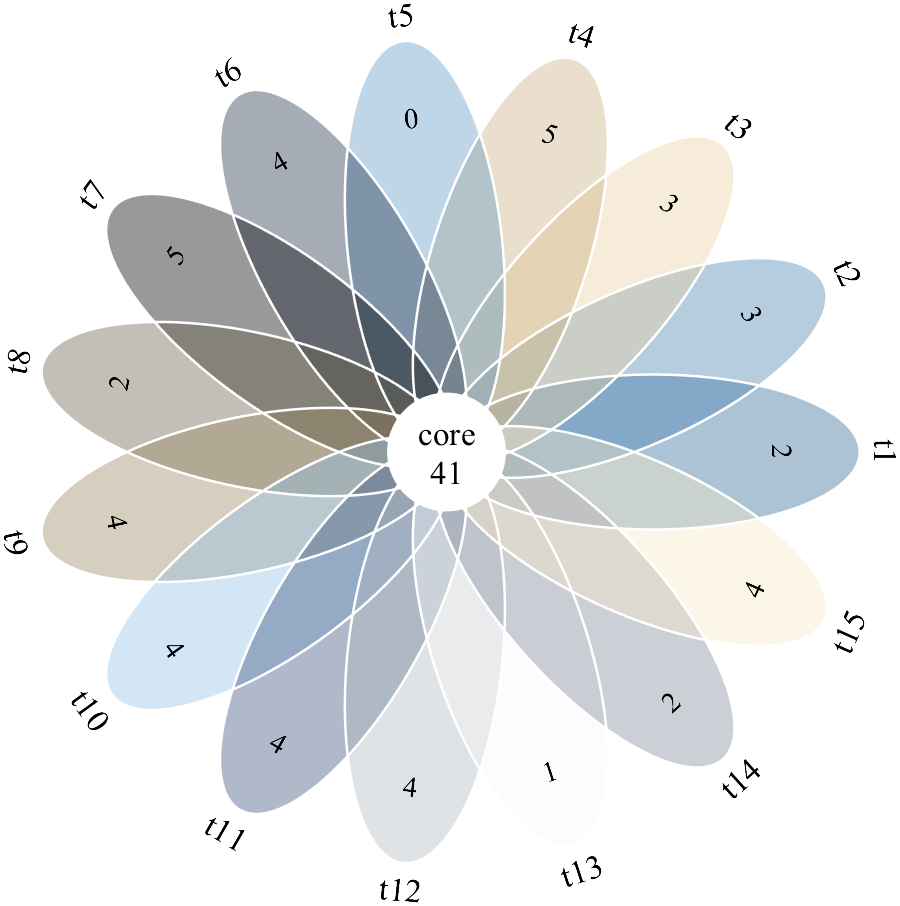


2 数据处理及图窗生成
% 数据计算
cT = linspace(0, 2*pi, 200);
cX = cos(cT).*8 + 8;
cY = sin(cT).*3;
cXY = [cX;cY];
setNum = size(Data, 2);
rT = 2*pi./setNum;
rM = [cos(rT),-sin(rT); sin(rT),cos(rT)];uniq = sum(Data.*(sum(Data,2) == 1),1);
core = sum(sum(Data,2) == setNum);figure('Units', 'normalized', 'Position', [.1,.1,.5,.8]);
ax=gca;
ax.NextPlot = 'add';
ax.DataAspectRatio = [1,1,1];
ax.XColor = 'none';
ax.YColor = 'none';
3 绘制花
% 绘制椭圆花瓣
for i = 0:setNum-1iXY = rM^i*cXY;fill(iXY(1,:), iXY(2,:), CList(i+1,:), 'FaceAlpha', .4, 'EdgeColor', 'none');
end
% 绘制白色边缘线
if 1
for i = 0:setNum-1iXY = rM^i*cXY;plot(iXY(1,:), iXY(2,:), 'Color', 'w', 'LineWidth', 1.2);
end
end
fill(cos(cT).*2.3, sin(cT).*2.3, [1,1,1], 'EdgeColor', 'none')

4 绘制文本
% 绘制文本信息
for i = 1:setNumtR = (i-1)*rT/pi*180;if tR>=0 && tR<=180tR = tR-90;elsetR = tR+90;endtext(cos((i-1)*rT).*13, sin((i-1)*rT).*13, num2str(uniq(i)),...'HorizontalAlignment', 'center',...'VerticalAlignment', 'middle',...'Rotation', tR,...numFont{:})text(cos((i-1)*rT).*17, sin((i-1)*rT).*17, setName{i},...'HorizontalAlignment', 'center',...'VerticalAlignment', 'middle',...'Rotation', tR,...labFont{:})
end
text(0, 0, {'core';num2str(core)},...'HorizontalAlignment', 'center',...'VerticalAlignment', 'middle',...labFont{:})
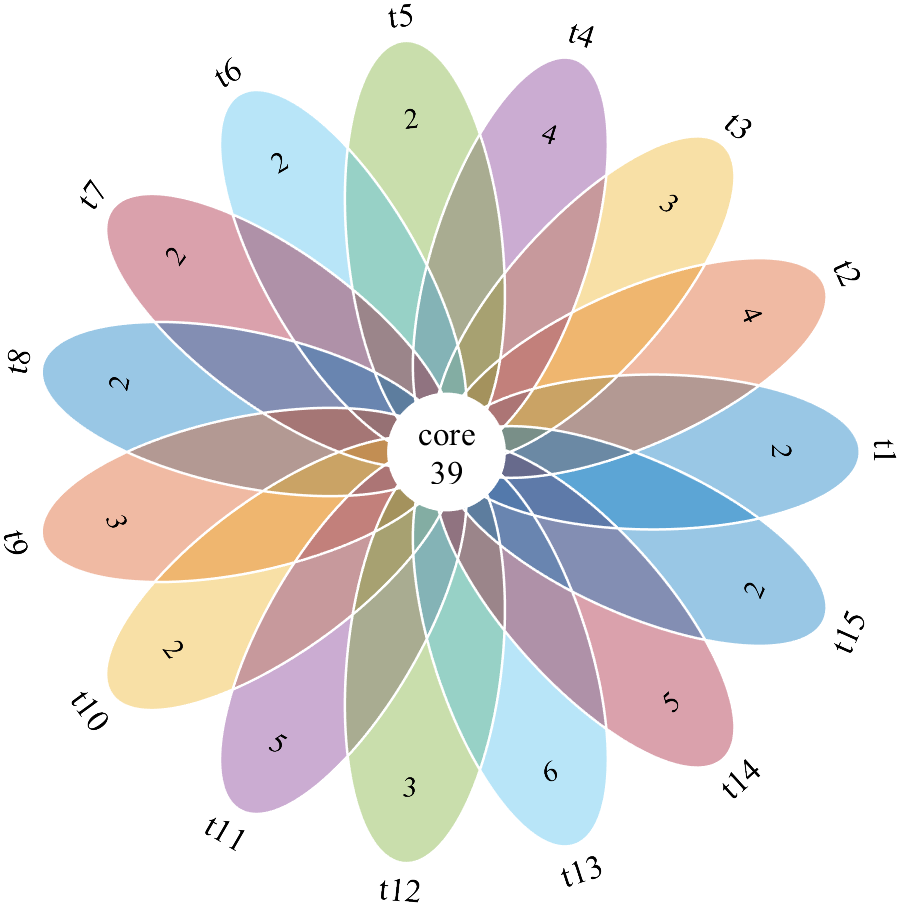
完整代码
% flowerPlotDemo% 给组起名t1 t2 t3...t15
setName = compose('t%d', 1:15);% 随机生成数据
Data = [rand(200, 15) > .1; rand(200, 15) > .85];% 设置字体
numFont = {'FontSize', 14, 'FontName', 'Times New Roman'};
labFont = {'FontSize', 16, 'FontName', 'Times New Roman'};% 设置配色
CList = lines(15);
% C = flowerPlotColor();
% CList = C.CList631;% =========================================================
% 绘图部分代码
% ---------------------------------------------------------
% 数据计算
cT = linspace(0, 2*pi, 200);
cX = cos(cT).*8 + 8;
cY = sin(cT).*3;
cXY = [cX;cY];
setNum = size(Data, 2);
rT = 2*pi./setNum;
rM = [cos(rT),-sin(rT); sin(rT),cos(rT)];uniq = sum(Data.*(sum(Data,2) == 1),1);
core = sum(sum(Data,2) == setNum);figure('Units', 'normalized', 'Position', [.1,.1,.5,.8]);
ax=gca;
ax.NextPlot = 'add';
ax.DataAspectRatio = [1,1,1];
ax.XColor = 'none';
ax.YColor = 'none';% 绘制椭圆花瓣
for i = 0:setNum-1iXY = rM^i*cXY;fill(iXY(1,:), iXY(2,:), CList(i+1,:), 'FaceAlpha', .4, 'EdgeColor', 'none');
end
% 绘制白色边缘线
if 1
for i = 0:setNum-1iXY = rM^i*cXY;plot(iXY(1,:), iXY(2,:), 'Color', 'w', 'LineWidth', 1.2);
end
end
fill(cos(cT).*2.3, sin(cT).*2.3, [1,1,1], 'EdgeColor', 'none')% 绘制文本信息
for i = 1:setNumtR = (i-1)*rT/pi*180;if tR>=0 && tR<=180tR = tR-90;elsetR = tR+90;endtext(cos((i-1)*rT).*13, sin((i-1)*rT).*13, num2str(uniq(i)),...'HorizontalAlignment', 'center',...'VerticalAlignment', 'middle',...'Rotation', tR,...numFont{:})text(cos((i-1)*rT).*17, sin((i-1)*rT).*17, setName{i},...'HorizontalAlignment', 'center',...'VerticalAlignment', 'middle',...'Rotation', tR,...labFont{:})
end
text(0, 0, {'core';num2str(core)},...'HorizontalAlignment', 'center',...'VerticalAlignment', 'middle',...labFont{:})
完
相关文章:

MATLAB | 情人节画个花瓣venn图?
之前七夕节情人节各种花,相册,爱心啥的都快画够了,今年画个花瓣韦恩图? 花瓣上的数字是仅属于该类的样本数,而中心的数字是属于每一类的样本数 教程部分 0 数据准备 % 给组起名t1 t2 t3...t15 setName compose(t%d,…...

[日常使用] Shell常用命令
Shell是什么? Shell简介 Shell是操作系统的外壳,是用户与操作系统内核之间的主要接口。它接收用户的命令并将其传递给内核执行,然后将执行结果返回给用户。Shell不仅是一个命令解释器,也是一种强大的编程语言。常见的Shell分为图…...
)
QT+OSG/osgEarth编译之八十七:osgdb_p3d+Qt编译(一套代码、一套框架,跨平台编译,版本:OSG-3.6.5插件库osgdb_p3d)
文章目录 一、osgdb_p3d介绍二、文件分析三、pro文件四、编译实践一、osgdb_p3d介绍 P3DXML是Panda3D引擎中使用的一种文件格式,用于描述3D场景的层次结构和属性。它是一种基于XML(eXtensible Markup Language)的文本格式,可以被Panda3D引擎读取和解析。 P3DXML文件包含了…...
寒假 day13
1.请编程实现二维数组的杨慧三角 #include<stdio.h> #include<string.h> int main(int argc, const char *argv[]) { int n,i,j;printf("please enter n:");scanf("%d",&n);int arr[n][n];for(i0;i<n;i){for(j0;j<i;j){if(j0 || ij…...

探索微信小程序的奇妙世界:从入门到进阶
文章目录 一、什么是微信小程序1.1 简要介绍微信小程序的定义和特点1.2 解释小程序与传统应用程序的区别 二、小程序的基础知识2.1 微信小程序的架构2.2 微信小程序生命周期的理解2.3 探索小程序的目录结构和文件类型 三、小程序框架和组件3.1 深入了解小程序框架的核心概念和原…...
-std::forward_list)
容器库(4)-std::forward_list
std::forward_list是可以从任何位置快速插入和移除元素的容器,不支持快速随机访问,只支持正向迭代。 本文章的代码库: https://gitee.com/gamestorm577/CppStd 成员函数 构造、析构和赋值 构造函数 可以用元素、元素列表、迭代器或者另…...

Netty Review - 服务端channel注册流程源码解析
文章目录 PreNetty主从Reactor线程模型服务端channel注册流程源码解读入口 serverBootstrap.bind(port) 源码流程图 Pre Netty Review - ServerBootstrap源码解析 Netty Review - NioServerSocketChannel源码分析 Netty主从Reactor线程模型 Netty 使用主从 Reactor 线程模型…...

冒泡排序平均需要跑多少趟:拉马努金Q函数初探
摘要: 拉马努金Q函数在算法分析中的应用,初步体验 【对算法,数学,计算机感兴趣的同学,欢迎关注我哈,阅读更多原创文章】 我的网站:潮汐朝夕的生活实验室 我的公众号:算法题刷刷 我的知乎&#x…...
Shell 学习笔记(三)-shell变量
Shell 语言是一种动态类型和弱类型语言, 因此,在Shell中无需显示地声明变量, 且变量的类型会根据不同的操作符而发生变化. 静态类型语言: 在程序编译期间就确定变量类型的语言, 如java, C等 动态类型语言: 在程序运行期间才确定变量类型的语言, 如PHP, Python等. 一 shell变量…...

新冠:2022和2024两次新冠感染的对比
第一次 2022年底第一次放开管控,95%以上的人都感染了一次奥密克戎 症状 第一天:流涕,咽痛。 第二天:高烧40度,全身疼痛,动不了。没有胃口,头晕想吐。 吃了白加黑退烧药,清开灵颗粒…...

笔记:《NCT全国青少年编程能力等级测试教程Python语言编程二级》
NCT全国青少年编程能力等级测试教程Python语言编程二级 ISBN:9787302565857 绪论 专题1 模块化编程 考查方向 考点清单 考点 模块化编程 (一)模块化编程思想:结构清晰、降低复杂度;提高代码复用率;易于扩展、维护,方便阅读、优化。 …...

顶级思维方式——认知篇五(思想的觉醒)
目录 1、 女性的地位觉醒 2、电视剧《天道》之高人思维:丁元英为什么讲“人间黑白颠倒”? 3、 创业公司, 更应该大胆的创新. 4、 做到一定职务的时候, 你一定想到在你这个地位上你要做什么 1、 女性的地位觉醒 过去引以为鉴的例子&…...

面试技术栈 —— 2024网易雷火暑期实习真题
面试技术栈 —— 2024网易雷火暑期实习真题 1. 最长递增子序列。2. 集中限流和单机限流你觉得哪个好?3. redis部署服务器配置,为什么不用哨兵?4. 讲讲分布式session的原理。5. 数据库:表数据量大了,如何分表࿱…...
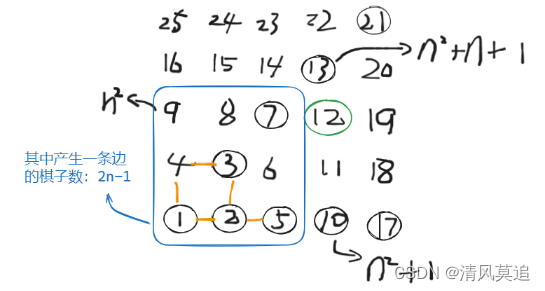
【小赛1】蓝桥杯双周赛第5场(小白)思路回顾
我的成绩:小白(5/6) 完稿时间:2024-2-13 比赛地址:https://www.lanqiao.cn/oj-contest/newbie-5/ 相关资料: 1、出题人题解:“蓝桥杯双周赛第5次强者挑战赛/小白入门赛”出题人题解 - 知乎 (zhihu.com) 2、矩阵快速幂&…...
-yum二进制部署)
docker (二)-yum二进制部署
yum安装docker(Linux) 安装环境:CentOS 7.9 一 如果之前安装了旧版docker,请先删除 sudo yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotat…...
)
【深度学习】S2 数学基础 P2 线性代数(下)
目录 范数的意义范数的数学意义范数之于深度学习的意义 L1 范数与 L2 范数L1 范数L2 范数 小结 本节博文是线性代数第二部分,主要内容为 L 1 L1 L1 范数与 L 2 L2 L2 范数;有关线性代数基础知识,请访问:【深度学习】S2 数学基础…...

【软考高级信息系统项目管理师--考试内容大纲篇】
🚀 作者 :“码上有前” 🚀 文章简介 :软考高级–信息系统项目管理师 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬 软考高级信息系统项目管理师--考试内容大纲篇 1.信息化发展2.信息技术发展3.信息系…...

C语言——枚举类型
📝前言: 在之前的文章中我们已经讲解了自定义类型中的结构体类型和联合体类型,现在我们再充分学习一下C语言中的枚举类型: 1,什么是枚举类型 2,枚举类型的定义和变量的声明 3,对变量进行赋值 &a…...

linux---内存管理
一 虚拟内存 即使是现代操作系统中,内存依然是计算机中很宝贵的资源,看看你电脑几个T固态硬盘,再看看内存大小就知道了。 为了充分利用和管理系统内存资源,Linux采用虚拟内存管理技术,利用虚拟内存技术让每个进程都有…...

v-model原理
v-model原理 v-model原理表单类组件封装v-model简化代码 v-model原理 1.原理: v-model本质上是一个语法糖。例如应用在输入框上,就是value属性 和 input 事件的合写 <template><div id"app" ><input v-model"msg"…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
