冒泡排序平均需要跑多少趟:拉马努金Q函数初探
摘要: 拉马努金Q函数在算法分析中的应用,初步体验【对算法,数学,计算机感兴趣的同学,欢迎关注我哈,原创文章】
我的网站:潮汐朝夕的生活实验室
我的公众号:算法题刷刷
我的知乎:潮汐朝夕
我的github:FennelDumplings
我的leetcode:FennelDumplings
各位好,本文我们继续来讨论算法分析中的问题。
很多数组上的算法都与 1 ∼ n 1 \sim n 1∼n 的排列有关,比如各种排序算法。在分析数组上的排序算法时,排列上的各种概念对分析问题很有用,比如逆序、圈、左向右最大值、上升、下降、游程、峰、谷等等。
本文我们看一下逆序的概念及其在冒泡排序的分析中的作用。然后我们解决一个相关的算法分析问题:对于 1 ∼ N 1 \sim N 1∼N 的随机排列, N → ∞ N \rightarrow\infty N→∞ 时,冒泡排序平均要跑多少趟。
首先给出结论, N → ∞ N \rightarrow\infty N→∞ 时,冒泡排序平均扫描趟数为 N − π N 2 + O ( 1 ) N - \sqrt{\frac{\pi N}{2}} + O(1) N−2πN+O(1)。
为了推导以上结论,我们首先介绍一下排列中关于逆序、逆序数、逆序表的概念。然后介绍一下冒泡排序算法的流程,然后根据逆序表的概念以及冒泡排序的流程,我们将冒泡排序平均扫描趟数问题转化为逆序表的最大值的问题。
之后我们在逆序表上经过一些组合分析,再结合数学期望的性质,将问题的答案写成了一个和式。于是原问题最终转化为了一个和式的渐近估阶的问题。
然后引用拉马努金Q函数相关的结论,对原和式化简,使得我们可以比较容易地对简化后的和式进行渐近估阶,得到最终结果。
排列的一些基本概念
记 p = p 1 p 2 ⋅ ⋅ ⋅ p N p = p_{1}p_{2}\cdot\cdot\cdot p_{N} p=p1p2⋅⋅⋅pN 为 1 ∼ N 1 \sim N 1∼N 的一个排列。
逆序:一个逆序是 i < j i < j i<j 且 p i > p j p_{i} > p_{j} pi>pj 的一个数对。
逆序表:记 q j q_{j} qj 表示 i ∈ [ 1.. j − 1 ] i \in [1..j-1] i∈[1..j−1] 中 p i > p j p_{i} > p_{j} pi>pj 的个数。 q = q 1 q 2 ⋅ ⋅ ⋅ q N q = q_{1}q_{2}\cdot\cdot\cdot q_{N} q=q1q2⋅⋅⋅qN 成为排列 p p p 的逆序表。
逆序数:记 σ ( p ) = ∑ j = 1 N q j \sigma(p) = \sum\limits_{j=1}\limits^{N}q_{j} σ(p)=j=1∑Nqj,表示排列 p p p 的逆序数。
排列与逆序表的一一对应
由以上定义可以知道,对于 1 ≤ j ≤ N 1 \leq j \leq N 1≤j≤N, q j q_{j} qj 需要满足约束 0 ≤ q j < j 0 \leq q_{j} < j 0≤qj<j。
给定满足该约束的任意一个序列 q = q 1 q 2 ⋅ ⋅ ⋅ q N q = q_{1}q_{2}\cdot\cdot\cdot q_{N} q=q1q2⋅⋅⋅qN,下面我们构造满足该逆序表 q q q 的排列 p p p。
对于 i = N , N − 1 , ⋯ , 1 i = N, N-1, \cdots, 1 i=N,N−1,⋯,1,置 p i p_{i} pi 为未曾用过的数中第 q i q_{i} qi 大的数,即可从右到左构造 p = p 1 p 2 ⋅ ⋅ ⋅ p N p = p_{1}p_{2}\cdot\cdot\cdot p_{N} p=p1p2⋅⋅⋅pN。
也就是说给定任意长为 N N N 的逆序表,至少可以构造出一个满足该逆序表的 1 ∼ N 1 \sim N 1∼N 的排列,下面我们说明该排列是唯一的。
由于 q i q_{i} qi 的取值范围 [ 0.. i − 1 ] [0..i-1] [0..i−1] 有 i i i 种可能,因此共有 N ! N! N! 种可能的逆序表 q = q 1 q 2 ⋅ ⋅ ⋅ q N q = q_{1}q_{2}\cdot\cdot\cdot q_{N} q=q1q2⋅⋅⋅qN。
另一方面我们熟知 1 ∼ N 1 \sim N 1∼N 的排列数为 N ! N! N!,如果在 N ! N! N! 个长为 N N N 的逆序表中,存在某个逆序表,其对应的排列不唯一,由鸽巢原理,就会出现某个 1 ∼ N 1 \sim N 1∼N 的排列对应两个不同的逆序表的情况,这与逆序表的定义矛盾。
因此长度为 N N N 的排列与逆序表之间存在一一对应关系。这对于我们分析冒泡排序非常有用。
冒泡排序算法
要对一个数组 p p p 排序,可以重复扫描这个数组。在一趟扫描过程中,假设扫描到 p [ i ] p[i] p[i] 时,如果 p [ i ] > p [ i + 1 ] p[i] > p[i + 1] p[i]>p[i+1],则将 p [ i ] p[i] p[i] 与 p [ i + 1 ] p[i+1] p[i+1] 交换,然后扫描下一个。否则直接扫描下一个。
如果在某趟扫描完成时,没有进行过任何交换,也就是每个元素都不比它后面的元素大,则排序就完成了。
由于每个交换都是两个相邻元素的交换,因此交换之后,逆序数减 1,这样总的交换次数恰好是一个排列中的逆序数。
另一方面,通过画图分析我们可以发现,一趟扫描完成后,逆序表中每个非零项的值都会减 1。当逆序表中所有项均为零时,程序结束。
这就隐含了:对一个排列的冒泡排序所需的趟数就等于逆序表中的最大元素。于是冒泡排序平均要跑多少趟,就等同于问:在 N ! N! N! 种可能的长为 N N N 的逆序表 q = q 1 q 2 ⋅ ⋅ ⋅ q N q = q_{1}q_{2}\cdot\cdot\cdot q_{N} q=q1q2⋅⋅⋅qN 中,最大值 max 1 ≤ j ≤ N q j \max\limits_{1\leq j \leq N} q_{j} 1≤j≤Nmaxqj 的平均值是多少。
逆序表中的最大值
对于 1 ∼ N 1 \sim N 1∼N 的排列,给定 0 ≤ k ≤ N 0 \leq k \leq N 0≤k≤N,考察所有项都小于 k k k 的逆序表的个数。
考察 q i q_{i} qi。如果 i ≤ k i \leq k i≤k, q i q_{i} qi 可以取 [ 0.. i − 1 ] [0..i-1] [0..i−1] 的任意值。当 i > k i > k i>k 时, q i q_{i} qi 可以取 [ 0.. k − 1 ] [0..k-1] [0..k−1] 之间的值。
于是 N ! N! N! 种长为 N N N 的逆序表中,所有项都小于 k k k,也就是最大项小于 k k k 的逆序表的个数为 k ! k N − k k!k^{N-k} k!kN−k。
因此 N ! N! N! 个长为 N 的逆序表中,最大项大于等于 k k k 的概率为 1 − k ! k N − k N ! 1 - \frac{k!k^{N-k}}{N!} 1−N!k!kN−k。
记 Q Q Q 为随机的长为 N N N 的逆序表中的最大值,于是我们已经得到 P ( Q ≥ k ) = 1 − k ! k N − k N ! P(Q \geq k) = 1 - \frac{k!k^{N-k}}{N!} P(Q≥k)=1−N!k!kN−k。
下面我们要求 E [ Q ] E[Q] E[Q]。这需要用到通过累积分布函数求数学期望的性质。
由累计分布函数求数学期望
我们知道,根据定义计算数学期望的一般方法如下。
X X X 为离散型,分布律为 P ( X = x ) P(X=x) P(X=x):
E [ X ] = ∑ x x P ( X = x ) E[X] = \sum\limits_{x}xP(X=x) E[X]=x∑xP(X=x)
X X X 为连续型,概率密度函数为 f ( x ) f(x) f(x):
E [ X ] = ∫ x f ( x ) d x E[X] = \int xf(x)\mathrm{d}x E[X]=∫xf(x)dx
但如果随机变量 X X X 非负,还可以有不经过分布律或概率密度函数的算法。
如果非负 X X X 为离散型,且已知 P ( X ≥ n ) P(X \geq n) P(X≥n),那么有:
E [ X ] = ∑ n = 0 ∞ P ( X ≥ n ) E[X] = \sum\limits_{n=0}\limits^{\infty}P(X\geq n) E[X]=n=0∑∞P(X≥n)
证明:
E [ X ] = ∑ x = 0 ∞ x P ( X = x ) = ∑ x = 0 ∞ ∑ n = 0 x P ( X = x ) = ∑ n = 0 ∞ ∑ x = n ∞ P ( X = x ) = ∑ n = 0 ∞ P ( X ≥ x ) \begin{aligned} E[X] &= \sum\limits_{x=0}\limits^{\infty}xP(X=x) \\ &= \sum\limits_{x=0}\limits^{\infty}\sum\limits_{n=0}\limits^{x}P(X=x) \\ &= \sum\limits_{n=0}\limits^{\infty}\sum\limits_{x=n}\limits^{\infty}P(X=x) \\ &= \sum\limits_{n=0}\limits^{\infty}P(X\geq x) \\ \end{aligned} E[X]=x=0∑∞xP(X=x)=x=0∑∞n=0∑xP(X=x)=n=0∑∞x=n∑∞P(X=x)=n=0∑∞P(X≥x)
□ \Box □
类似地,如果非负 X X X 为连续型,且其累积分布函数为 F ( x ) F(x) F(x),那么有:
E [ X ] = ∫ 0 ∞ ( 1 − F ( x ) ) d x E[X] = \int_{0}^{\infty}(1 - F(x))\mathrm{d}x E[X]=∫0∞(1−F(x))dx
证明:
E [ X ] = ∫ 0 ∞ y f ( y ) d y = ∫ 0 ∞ ∫ 0 y f ( y ) d x d y = ∫ 0 ∞ ∫ x ∞ f ( y ) d y d x = ∫ 0 ∞ ( 1 − F ( x ) ) d x \begin{aligned} E[X] &= \int_{0}^{\infty}yf(y)\mathrm{d}y \\ &= \int_{0}^{\infty}\int_{0}^{y}f(y)\mathrm{d}x\mathrm{d}y \\ &= \int_{0}^{\infty}\int_{x}^{\infty}f(y)\mathrm{d}y\mathrm{d}x \\ &= \int_{0}^{\infty}(1 - F(x))\mathrm{d}x \\ \end{aligned} E[X]=∫0∞yf(y)dy=∫0∞∫0yf(y)dxdy=∫0∞∫x∞f(y)dydx=∫0∞(1−F(x))dx
□ \Box □
问题规约:拉马努金Q函数
根据前面对逆序表的分析,以及上述数学期望的性质,长为 N N N 的逆序表的最大值的期望如下:
∑ k = 0 N ( 1 − k ! k N − k N ! ) = N + 1 − ∑ k = 0 N k ! k N − k N ! \sum\limits_{k=0}\limits^{N}(1 - \frac{k!k^{N-k}}{N!}) = N + 1 - \sum\limits_{k=0}\limits^{N}\frac{k!k^{N-k}}{N!} k=0∑N(1−N!k!kN−k)=N+1−k=0∑NN!k!kN−k
于是最初的问题最终归结到了对 ∑ k = 0 N k ! k N − k N ! \sum\limits_{k=0}\limits^{N}\frac{k!k^{N-k}}{N!} k=0∑NN!k!kN−k 的渐近估阶。
对以上和式做下标变换:
∑ k = 0 N k ! k N − k N ! = ∑ k = 0 N ( N − k ) ! ( N − k ) k N ! \sum\limits_{k=0}\limits^{N}\frac{k!k^{N-k}}{N!} = \sum\limits_{k=0}\limits^{N}\frac{(N-k)!(N-k)^{k}}{N!} \\ k=0∑NN!k!kN−k=k=0∑NN!(N−k)!(N−k)k
记 f N ( k ) = ( N − k ) ! ( N − k ) k N ! f_{N}(k) = \frac{(N-k)!(N-k)^{k}}{N!} fN(k)=N!(N−k)!(N−k)k,下面推导 f N ( k ) f_{N}(k) fN(k):
f N ( k ) = ( N − k ) ! ( N − k ) k N ! = N − k N ⋅ N − k N − 1 ⋅ ⋅ ⋅ N − k N − k + 1 = ( 1 − k N ) ⋅ ( 1 − k − 1 N − 1 ) ⋅ ⋅ ⋅ ( 1 − 1 N − k + 1 ) = ∏ i = 1 k ( 1 − i N − k + i ) \begin{aligned} f_{N}(k) &= \frac{(N-k)!(N-k)^{k}}{N!} \\ &= \frac{N-k}{N}\cdot \frac{N-k}{N-1} \cdot\cdot\cdot \frac{N-k}{N-k+1} \\ &= (1 - \frac{k}{N})\cdot (1 - \frac{k-1}{N-1}) \cdot\cdot\cdot (1 - \frac{1}{N-k+1}) \\ &= \prod\limits_{i=1}\limits^{k}(1 - \frac{i}{N-k+i}) \\ \end{aligned} fN(k)=N!(N−k)!(N−k)k=NN−k⋅N−1N−k⋅⋅⋅N−k+1N−k=(1−Nk)⋅(1−N−1k−1)⋅⋅⋅(1−N−k+11)=i=1∏k(1−N−k+ii)
后续的处理非常复杂,需要对 k 较小和 k 很大的情况分别讨论,比较冗长,其完整推导过程与拉马努金 Q 函数的推导过程类似,这里直接引用结论,如下:
∑ k = 0 N k ! k N − k N ! = ∑ k = 0 N f N ( k ) = ∑ k = 0 N e − k 2 2 N + O ( 1 ) N → ∞ \sum\limits_{k=0}\limits^{N}\frac{k!k^{N-k}}{N!} = \sum\limits_{k=0}\limits^{N}f_{N}(k) = \sum\limits_{k=0}\limits^{N}e^{-\frac{k^{2}}{2N}} + O(1) \quad\quad N\rightarrow\infty k=0∑NN!k!kN−k=k=0∑NfN(k)=k=0∑Ne−2Nk2+O(1)N→∞
以后有时间可以再回来看一下上式的推导过程,感兴趣的可以看《算法分析导论》或《计算机程序设计艺术》中关于拉马努金Q函数的内容。
积分逼近求和
下面对 ∑ k = 0 ∞ e − k 2 2 N \sum\limits_{k=0}\limits^{\infty}e^{-\frac{k^{2}}{2N}} k=0∑∞e−2Nk2 进行估阶。记 h ( x ) = e − x 2 2 N h(x) = e^{-\frac{x^{2}}{2N}} h(x)=e−2Nx2。可以用积分逼近求和:
∑ k = 0 ∞ e − k 2 2 N = ∫ 0 ∞ e − x 2 2 N d x + Δ = 2 N ∫ 0 ∞ e − ( x 2 N ) 2 d x 2 N + Δ = 2 N ∫ 0 ∞ e − t 2 d t + Δ = 2 N π 2 + Δ \begin{aligned} \sum\limits_{k=0}\limits^{\infty}e^{-\frac{k^{2}}{2N}} &= \int_{0}^{\infty}e^{-\frac{x^{2}}{2N}}\mathrm{d}x + \Delta \\ &= \sqrt{2N}\int_{0}^{\infty}e^{-(\frac{x}{\sqrt{2N}})^{2}}\mathrm{d}\frac{x}{\sqrt{2N}} + \Delta \\ &= \sqrt{2N}\int_{0}^{\infty}e^{-t^{2}}\mathrm{d}t + \Delta \\ &= \sqrt{2N}\frac{\sqrt{\pi}}{2} + \Delta \\ \end{aligned} k=0∑∞e−2Nk2=∫0∞e−2Nx2dx+Δ=2N∫0∞e−(2Nx)2d2Nx+Δ=2N∫0∞e−t2dt+Δ=2N2π+Δ
由于 h ( x ) h(x) h(x) 在 x ≥ 0 x \geq 0 x≥0 上是单调递减函数, Δ ≤ ∣ h ( 0 ) − h ( ∞ ) ∣ = 1 \Delta \leq |h(0) - h(\infty)| = 1 Δ≤∣h(0)−h(∞)∣=1,于是有:
∑ k = 0 ∞ e − k 2 2 N = π N 2 + O ( 1 ) \sum\limits_{k=0}\limits^{\infty}e^{-\frac{k^{2}}{2N}} = \sqrt{\frac{\pi N}{2}} + O(1) k=0∑∞e−2Nk2=2πN+O(1)
上式通过欧拉-麦克劳林公式也可以导出,但由于 h ( x ) h(x) h(x) 的单调性,直接用积分逼近求和更简单一些。最终结果为:
N + 1 − ∑ k = 0 N k ! k N − k N ! = N − π N 2 + O ( 1 ) N → ∞ N + 1 - \sum\limits_{k=0}\limits^{N}\frac{k!k^{N-k}}{N!} = N - \sqrt{\frac{\pi N}{2}} + O(1) \quad\quad N\rightarrow\infty N+1−k=0∑NN!k!kN−k=N−2πN+O(1)N→∞
也就是, N → ∞ N \rightarrow\infty N→∞ 时,冒泡排序平均扫描趟数为 N − π N 2 + O ( 1 ) N - \sqrt{\frac{\pi N}{2}} + O(1) N−2πN+O(1)。
总结
本文我们讨论了排序算法的分析中的一个问题:冒泡排序平均需要跑多少趟。
首先引入了排列中的一些概念定义,包括逆序、逆序表,然后基于冒泡排序的算法流程,发现冒泡排序扫描的趟数就是逆序表中的最大值。
再结合排列的逆序表自身的性质,以及通过累积分布函数求数学期望的性质,最终我们将问题归结到了 ∑ k = 0 N k ! k N − k N ! \sum\limits_{k=0}\limits^{N}\frac{k!k^{N-k}}{N!} k=0∑NN!k!kN−k 的渐近估阶。
上式的渐近估阶非常麻烦冗长,我们参考了《计算机程序设计艺术》、《算法分析导论》等名著中关于拉马努金Q函数的相关论述,直接引用结果,将问题转化为 ∑ k = 0 ∞ e − k 2 2 N \sum\limits_{k=0}\limits^{\infty}e^{-\frac{k^{2}}{2N}} k=0∑∞e−2Nk2 的进行估阶。而后者通过积分逼近求和的方式或者欧拉-麦克劳林公式你可以方便解决。
最终我们得出结论, N → ∞ N \rightarrow\infty N→∞ 时,冒泡排序平均扫描趟数为 N − π N 2 + O ( 1 ) N - \sqrt{\frac{\pi N}{2}} + O(1) N−2πN+O(1)。通过这个例子我们看到,使用拉马努金 Q 函数可以将某些难解的和式简化。
算法分析中使用拉马努金 Q 函数的例子非常多,关于拉马努金 Q 函数的前因后果,以及更多的应用,后续再跟大家探讨。
相关文章:

冒泡排序平均需要跑多少趟:拉马努金Q函数初探
摘要: 拉马努金Q函数在算法分析中的应用,初步体验 【对算法,数学,计算机感兴趣的同学,欢迎关注我哈,阅读更多原创文章】 我的网站:潮汐朝夕的生活实验室 我的公众号:算法题刷刷 我的知乎&#x…...
Shell 学习笔记(三)-shell变量
Shell 语言是一种动态类型和弱类型语言, 因此,在Shell中无需显示地声明变量, 且变量的类型会根据不同的操作符而发生变化. 静态类型语言: 在程序编译期间就确定变量类型的语言, 如java, C等 动态类型语言: 在程序运行期间才确定变量类型的语言, 如PHP, Python等. 一 shell变量…...

新冠:2022和2024两次新冠感染的对比
第一次 2022年底第一次放开管控,95%以上的人都感染了一次奥密克戎 症状 第一天:流涕,咽痛。 第二天:高烧40度,全身疼痛,动不了。没有胃口,头晕想吐。 吃了白加黑退烧药,清开灵颗粒…...

笔记:《NCT全国青少年编程能力等级测试教程Python语言编程二级》
NCT全国青少年编程能力等级测试教程Python语言编程二级 ISBN:9787302565857 绪论 专题1 模块化编程 考查方向 考点清单 考点 模块化编程 (一)模块化编程思想:结构清晰、降低复杂度;提高代码复用率;易于扩展、维护,方便阅读、优化。 …...

顶级思维方式——认知篇五(思想的觉醒)
目录 1、 女性的地位觉醒 2、电视剧《天道》之高人思维:丁元英为什么讲“人间黑白颠倒”? 3、 创业公司, 更应该大胆的创新. 4、 做到一定职务的时候, 你一定想到在你这个地位上你要做什么 1、 女性的地位觉醒 过去引以为鉴的例子&…...

面试技术栈 —— 2024网易雷火暑期实习真题
面试技术栈 —— 2024网易雷火暑期实习真题 1. 最长递增子序列。2. 集中限流和单机限流你觉得哪个好?3. redis部署服务器配置,为什么不用哨兵?4. 讲讲分布式session的原理。5. 数据库:表数据量大了,如何分表࿱…...
【小赛1】蓝桥杯双周赛第5场(小白)思路回顾
我的成绩:小白(5/6) 完稿时间:2024-2-13 比赛地址:https://www.lanqiao.cn/oj-contest/newbie-5/ 相关资料: 1、出题人题解:“蓝桥杯双周赛第5次强者挑战赛/小白入门赛”出题人题解 - 知乎 (zhihu.com) 2、矩阵快速幂&…...
-yum二进制部署)
docker (二)-yum二进制部署
yum安装docker(Linux) 安装环境:CentOS 7.9 一 如果之前安装了旧版docker,请先删除 sudo yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotat…...
)
【深度学习】S2 数学基础 P2 线性代数(下)
目录 范数的意义范数的数学意义范数之于深度学习的意义 L1 范数与 L2 范数L1 范数L2 范数 小结 本节博文是线性代数第二部分,主要内容为 L 1 L1 L1 范数与 L 2 L2 L2 范数;有关线性代数基础知识,请访问:【深度学习】S2 数学基础…...

【软考高级信息系统项目管理师--考试内容大纲篇】
🚀 作者 :“码上有前” 🚀 文章简介 :软考高级–信息系统项目管理师 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬 软考高级信息系统项目管理师--考试内容大纲篇 1.信息化发展2.信息技术发展3.信息系…...

C语言——枚举类型
📝前言: 在之前的文章中我们已经讲解了自定义类型中的结构体类型和联合体类型,现在我们再充分学习一下C语言中的枚举类型: 1,什么是枚举类型 2,枚举类型的定义和变量的声明 3,对变量进行赋值 &a…...

linux---内存管理
一 虚拟内存 即使是现代操作系统中,内存依然是计算机中很宝贵的资源,看看你电脑几个T固态硬盘,再看看内存大小就知道了。 为了充分利用和管理系统内存资源,Linux采用虚拟内存管理技术,利用虚拟内存技术让每个进程都有…...

v-model原理
v-model原理 v-model原理表单类组件封装v-model简化代码 v-model原理 1.原理: v-model本质上是一个语法糖。例如应用在输入框上,就是value属性 和 input 事件的合写 <template><div id"app" ><input v-model"msg"…...
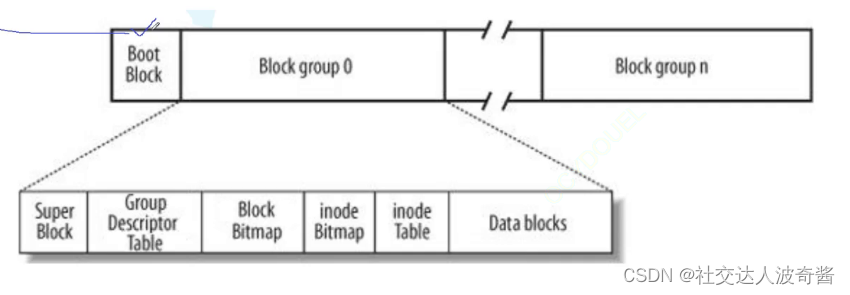
波奇学Linux:文件系统
磁盘认识 磁盘被访问的基本单元是扇区-512字节。 磁盘可以看成多个同心圆,每个同心圆叫做磁道,多个扇区组成同心圆。 我们可以把磁盘看做由无数个扇区构成的存储介质。 要把数据存到磁盘,先定位扇区,用哪一个磁头,…...

项目访问量激增该如何应对
✨✨ 欢迎大家来到喔的嘛呀的博客✨✨ 🎈🎈希望这篇博客对大家能有帮助🎈🎈 目录 引言 一. 优化数据库 1.1 索引优化 1.2 查询优化 1.3 数据库设计优化 1.4 事务优化 1.5 硬件优化 1.6 数据库配置优化 二. 增加服务器资源…...

【Linux环境基础开发工具的使用(yum、vim、gcc、g++、gdb、make/Makefile)】
Linux环境基础开发工具的使用yum、vim、gcc、g、gdb、make/Makefile Linux软件包管理器- yumLinux下安装软件的方式认识yum查找软件包安装软件如何实现本地机器和云服务器之间的文件互传卸载软件 Linux编辑器 - vimvim的基本概念vim下各模式的切换vim命令模式各命令汇总vim底行…...
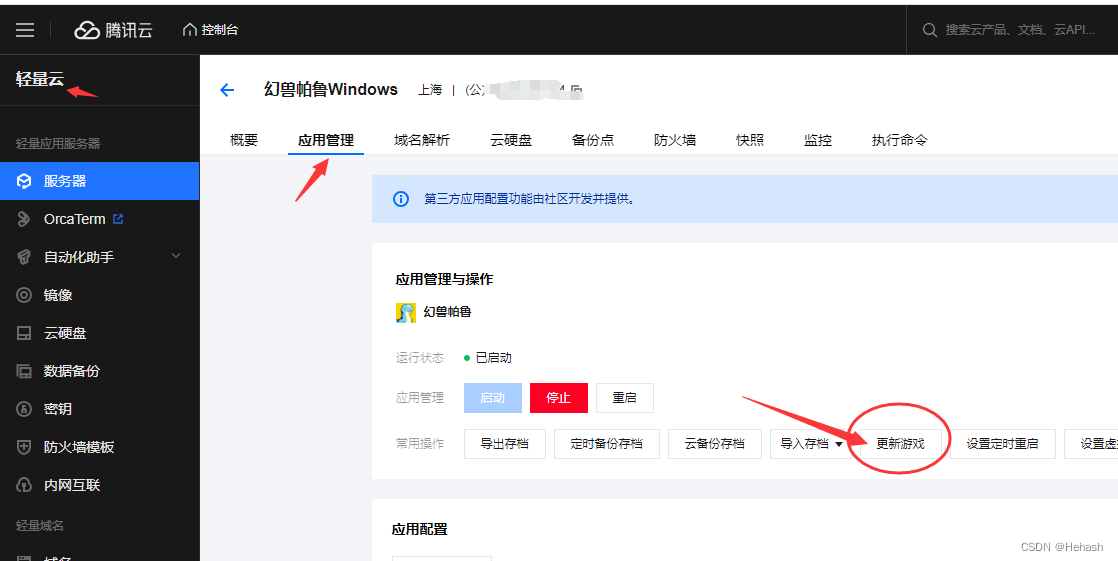
幻兽帕鲁官方更新了,服务器端怎么更新?
幻兽帕鲁官方客户端更新了,那么它的服务器端版本也是需要更新的,不然版本不一致的话,就不能进入游戏了。 具体的更新方法有两种,一是手动输入命令进行更新。第二种是在面板一键更新。 无论你是在阿里云或者腾讯云购买的一键部署…...

axios-retry 响应异常
最近项目中遇到 axios 异步请求异常中断, 错误码为 “ECONNABORTED” 奇怪的是排查前端代码并没有发现有主动调用 abort 取消请求的 由于为何网络请求失败的原因找不到, 但是重试请求就是成功的, 所以计划使用 axios-retry 在网络错误时重新请求 import axiosRetry from axios…...
Vue项目创建和nodejs使用
Vue项目创建和nodejs使用 一、环境准备1.1.安装 node.js【下载历史版本node-v14.21.3-x64】1.2.安装1.3.检查是否安装成功:1.4.在Node下新建两个文件夹 node_global和node_cache并设置权限1.5.配置npm在安装全局模块时的路径和缓存cache的路径1.6.配置系统变量&…...

【机器学习案例3】从科学论文图片中提取标题、作者和摘要【含源码】
在这个项目中,我的目标是从科学论文图片中提取某些部分(标题、作者和摘要)。预期提取部分是科学论文中常见的部分,例如标题、摘要和作者。输入与最终结果。我的输入是将第一页纸转换成图像。最终结果是一个 txt 文件,其中包含标题、作者和摘要部分,如下图1和图2所示。我将…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
