LeetCode 二叉树/n叉树的解题思路
二叉树
- 二叉树特点是每个节点最多只能有两棵子树,且有左右之分
- 二叉树的数据结构如下:
public class TreeNode {//节点的值int val;//左子树TreeNode left;//右子树TreeNode right;TreeNode(int x) { val = x; }
}
- 树节点的初始化:
int val=1;TreeNode node = new TreeNode(val);
- 获取树的节点node的值:
int val = node.val;
- 二叉树的节点为node,求左右子树:
TreeNode right =node.right;TreeNode left= node.left;
- N叉树的节点结构如下:
class Node {public int val;public List<Node> children;
}
树的遍历
树的遍历方式有:前序遍历(又叫先序遍历)、中序遍历、后序遍历
前序遍历:根节点,左节点,右节点。
中序遍历:左节点,根节点,右节点。
后序遍历:左节点,右节点,根节点。
递归法
树经常会用到递归。
- 比如二叉树的中序遍历(LeetCode94)。
先序遍历、后序遍历也类似,只是调换了节点的顺序而已。
public class LeetCode94 {//list设置为成员变量,如果是方法内变量,无法一直添加元素private List<Integer> list = new ArrayList<>();public List<Integer> inorderTraversal(TreeNode root) {if (root == null) {return list;}//中序遍历:左节点,根节点,右节点。inorderTraversal(root.left);list.add(root.val);inorderTraversal(root.right);return list;}
}
- 比如N叉树的前序遍历(LeetCode589)。
class LeetCode589{//list设置为成员变量,如果是方法内变量,无法一直添加元素private List<Integer> list = new LinkedList<>();public List<Integer> preorder(Node root) {if(root==null) {return list;}list.add(root.val);for (Node node : root.children) {preorder(node);}return list;}
}
迭代法
- 树还可以用迭代法。利用栈的先进后出解题。
迭代法是DFS和BFS的基础,可以多学习一下。
BFS(广度优先搜索算法)。
BFS的操作步骤如下:
1、使用 Queue的 offer()方法(或者是add()方法)把树的根节点放入 Queue;
2、重复以下步骤,直到 Queue为空为止(也就是while循环条件为 !queue.isEmpty()):
(1)获取 Queue的size, 因为Queue中存放的其实就是每一层中所有的节点, size就相当于每一层的数量,也就是宽度
(2)遍历队列,直到当前这一层所有的节点都遍历完(也就是while循环条件为 size-- > 0 )
(3)在遍历过程中,使用 Queue的 offer()方法得到队列中的节点,根据节点查出它的左节点和右节点,并用offer()方法放入队列中。
题目:LeetCode104、LeetCode102
- leetCode102:二叉树的层序遍历
public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> resultList = new ArrayList<>();if (root==null) {return resultList;}Queue<TreeNode> queue = new ArrayDeque<>();queue.add(root);//遍历队列while (!queue.isEmpty()) {//此处有坑,一定要先把每一层的数量记录下来,不然队列的长度发生变化,遍历次数不一样int n=queue.size();//层序遍历,从最上层到最下层,可以用BFS,把每一层的节点放到list里面。//每一层都有一个listList<Integer> list = new ArrayList<>();for (int i=0;i<n;i++) {//用poll拿出队列的节点TreeNode node = queue.poll();list.add(node.val);//把当前节点的左子节点、右子节点,放入到队列中。if (node.left!=null) {queue.add(node.left);}if (node.right!=null) {queue.add(node.right);}}resultList.add(list);}return resultList;}
}
- LeetCode104:求二叉树的最大深度。
public class LeetCode104BFS {public int maxDepth(TreeNode root) {if (root == null){return 0;}int depth = 0;Queue<TreeNode> queue= new LinkedList<>();//队列使用offer和poll不会抛异常//首先,要将根节点放入队列中。nodes.offer(root);while (!queue.isEmpty()) {//队列中存放的其实就是每一层中所有的节点//size就相当于每一层的数量int size = queue.size();//遍历一次,深度就加一depth++;//遍历队列中的数据,直到当前这一层所有的节点都遍历完while (size-- > 0) {//取出队列中的树节点TreeNode node = queue.poll();//将当前节点的左右子树,放入队列中。if (node!=null && node.left != null){queue.offer(node.left);}if (node!=null && node.right != null){queue.offer(node.right);}}}return depth;}
}
DFS(深度优先搜索算法)
以深度优先为策略,从根节点开始一直遍历到某个叶子节点。
DFS的实现方式相比于BFS应该说大同小异,只是把 queue 换成了stack而已,stack具有后进先出LIFO(Last Input First Output)的特性,DFS的操作步骤如下:
1、把起始点放入stack;
2、重复下述3步骤,直到stack为空为止:
(1)从stack中访问栈顶的点;
(2)找出与此点邻接的且尚未遍历的点(也就是子节点),进行标记,然后全部放入stack中;
(3)如果此点没有尚未遍历的邻接点,则将此点从stack中弹出。
- LeetCode589:N叉树的前序遍历。
class Solution {public List<Integer> preorder(Node root) {List<Integer> list = new ArrayList<>();if (root == null) return list;//将根节点数据添加到栈中Stack<Node> stack = new Stack<>();stack.add(root);while (!stack.empty()) {//栈顶的数据,出栈root = stack.pop();//在list中添加栈顶数据list.add(root.val);//将子节点全部放入栈里面,由于栈是后进先出,所以后面的子节点先放入for (int i = root.children.size() - 1; i >= 0; i--)stack.add(root.children.get(i));}return list;}
}
参考资料
leetCode
相关文章:

LeetCode 二叉树/n叉树的解题思路
二叉树 二叉树特点是每个节点最多只能有两棵子树,且有左右之分二叉树的数据结构如下: public class TreeNode {//节点的值int val;//左子树TreeNode left;//右子树TreeNode right;TreeNode(int x) { val x; } }树节点的初始化: int val1;T…...
opencv mat用法赋值克隆的操作和一些基本属性
//Mat基本结构 (头部 数据部分) //赋值的话 就是修改了指针位置 但还是指向了原来数据 并没创建数据 本质上并没有变 //只有克隆或者拷贝时 它才会真正复制一份数据 //代码实现 //创建方法 - 克隆 //Mat m1 src.clone(); //复制 //Mat m2; //src.copyTo(m2); //赋值法 …...
【使用IDEA总结】01——新增作者信息、方法参数返回值
[TOC](目录) 1.类新增作者信息 打开IDEA的Settings,Editor->Code Style->File and Code Templates->Includes->File Header,输入以下作者信息,作者名更换为自己的即可,操作如下图所示 /*** Author Linhaipeng* Date…...
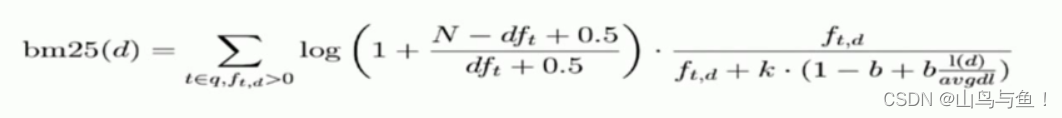
ElasticSearch分词器和相关性详解
目录 ES分词器详解 基本概念 分词发生时期 分词器的组成 切词器:Tokenizer 词项过滤器:Token Filter 停用词 同义词 字符过滤器:Character Filter HTML 标签过滤器:HTML Strip Character Filter 字符映射过滤器&#x…...
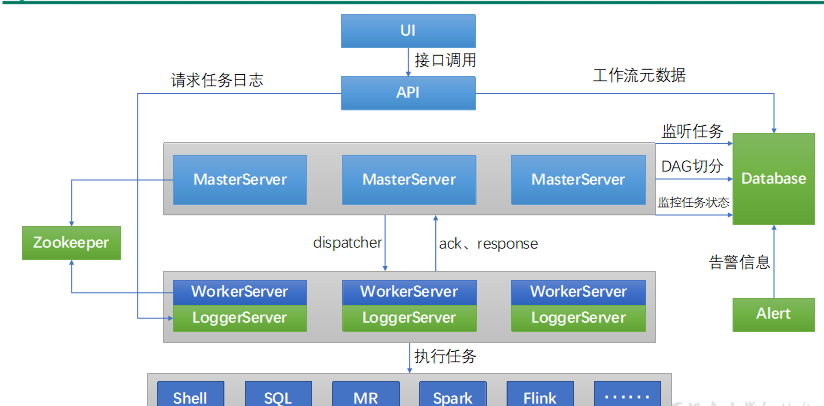
DolphinScheduler安装与配置
DolphinScheduler概述 Apache DolphinScheduler是一个分布式、易扩展的可视化DAG工作流任务调度平台。致力于解决数据处理流程中错综复杂的依赖关系,使调度系统在数据处理流程中开箱即用。 DolphinScheduler的主要角色如下: MasterServer采用分布式无…...
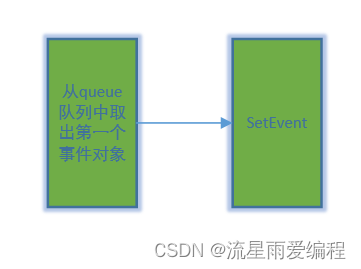
Qt之条件变量QWaitCondition详解
QWaitCondition内部实现结构图: 相关系列文章 C之Pimpl惯用法 目录 1.简介 2.示例 2.1.全局配置 2.2.生产者Producer 2.3.消费者Consumer 2.4.测试例子 3.原理分析 3.1.辅助函数CreateEvent 3.2.辅助函数WaitForSingleObject 3.3.QWaitConditionEvent …...
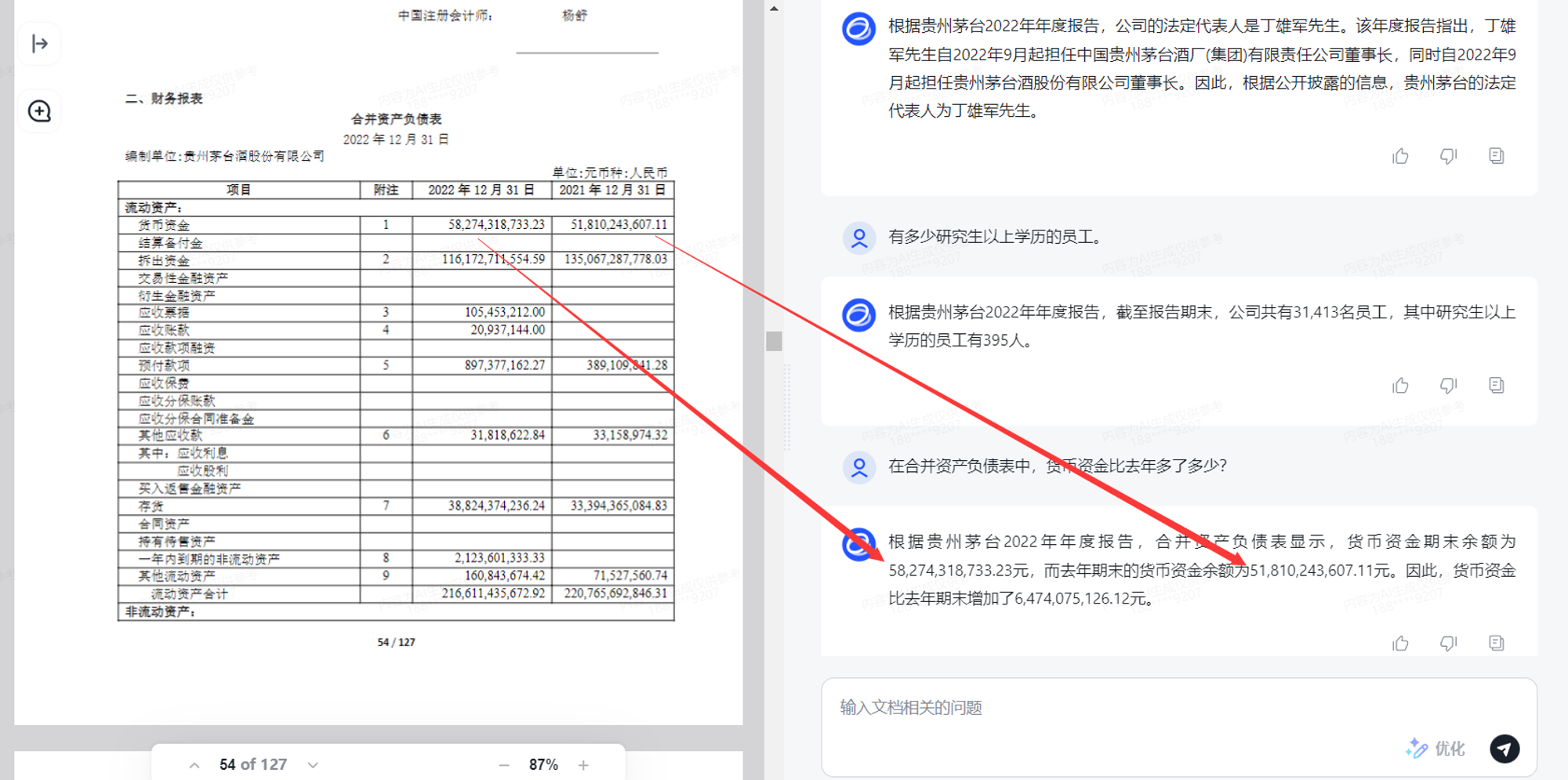
作为国产大模型之光的智谱AI,究竟推出了多少模型?一篇文章带你详细了解!
虽然OpenAI发布了一系列基于GPT模型的产品,在不同领域取得了很高的成就。但是作为LLM领域绝对的领头羊,OpenAI没有按照其最初的Open初衷行事。无论是ChatGPT早期采用的GPT3,还是后来推出的GPT3.5和GPT4模型,OpenAI都因为担心被滥用…...

学习转置矩阵
转置矩阵 将矩阵的行列互换得到的新矩阵称为转置矩阵 输入描述: 第一行包含两个整数n和m,表示一个矩阵包含n行m列,用空格分隔。 (1≤n≤10,1≤m≤10) 从2到n1行,每行输入m个整数(范围-231~231-1)&#x…...

AJAX——常用请求方法
1 请求方法 请求方法:对服务器资源,要执行的操作 2 数据提交 场景:当数据需要在服务器上保存 3 axios请求配置 url:请求的URL网址 method:请求的方法,GET可以省略(不区分大小写) …...

sqlserver2012 解决日志大的问题
当SQL Server 2012的事务日志变得过大时,这通常意味着日志备份没有被定期执行,或者日志文件的自动增长设置被设置得太高,导致它不断增长以容纳所有未备份的事务。解决日志大的问题通常涉及以下几个步骤: 备份事务日志:…...
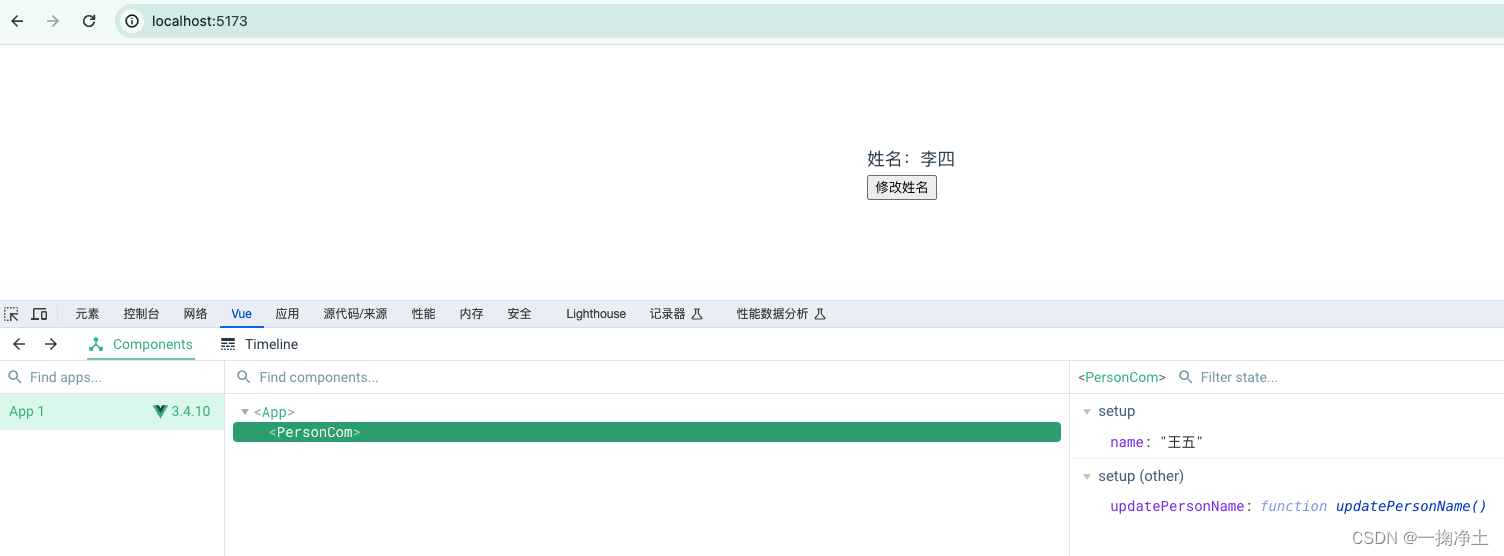
Vue3快速上手(三)Composition组合式API及setup用法
一、Vue2的API风格 Vue2的API风格是Options API,也叫配置式API。一个功能的数据,交互,计算,监听等都是分别配置在data, methods,computed, watch等模块里的。如下: <template><div class"person"…...
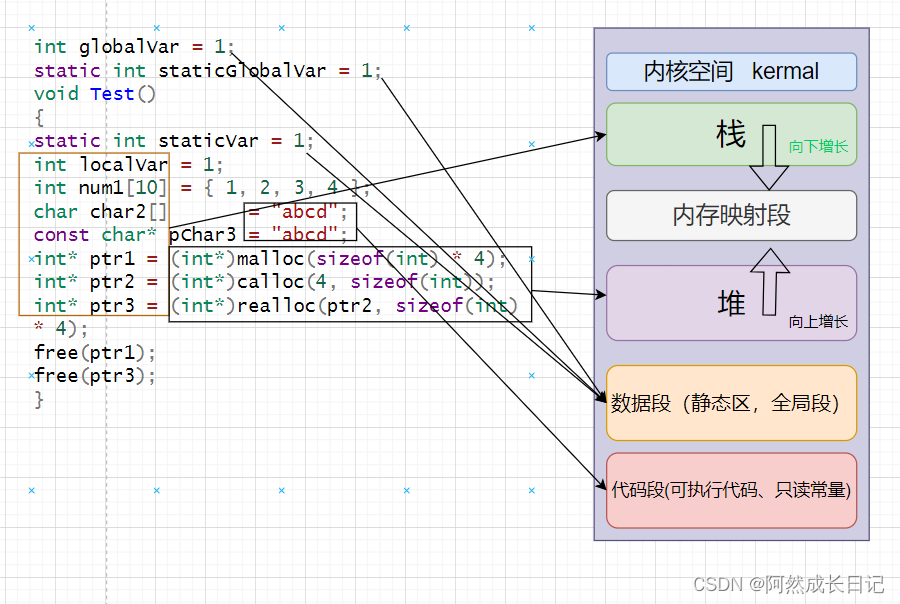
【C++】内存五大区详解
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...
Django学习笔记教程全解析:初步学习Django模型,初识API,以及Django的后台管理系统(Django全解析,保姆级教程)
把时间用在思考上是最能节省时间的事情。——[美]卡曾斯 导言 写在前面 本文部分内容引用的是Django官方文档,对官方文档进行了解读和理解,对官方文档的部分注释内容进行了翻译,以方便大家的阅读和理解。 概述 在上一篇文章里࿰…...

Python学习之路-爬虫提高:selenium
Python学习之路-爬虫提高:selenium 什么是selenium Selenium是一个Web的自动化测试工具,最初是为网站自动化测试而开发的,Selenium 可以直接运行在浏览器上,它支持所有主流的浏览器(包括PhantomJS这些无界面的浏览器)…...
Rust基础拾遗--进阶
Rust基础拾遗 前言1.结构体1.1 具名字段型结构体1.2 元组型结构体1.3 单元型结构体1.4 结构体布局1.5 用impl定义方法1.5.1 以Box、Rc或Arc形式传入self1.5.2 类型关联函数 1.6 关联常量1.7 泛型结构体1.8 带生命周期参数的泛型结构体1.9 带常量参数的泛型结构体1.10 让结构体类…...

数据同步工具对比——SeaTunnel 、DataX、Sqoop、Flume、Flink CDC
在大数据时代,数据的采集、处理和分析变得尤为重要。业界出现了多种工具来帮助开发者和企业高效地处理数据流和数据集。本文将对比五种流行的数据处理工具:SeaTunnel、DataX、Sqoop、Flume和Flink CDC,从它们的设计理念、使用场景、优缺点等方…...

随机过程及应用学习笔记(四) 马尔可夫过程
马尔可夫过程是理论上和实际应用中都十分重要的一类随机过程。 目录 前言 一、马尔可夫过程的概念 二、离散参数马氏链 1 定义 2 齐次马尔可夫链 3 齐次马尔可夫链的性质 三、齐次马尔可夫链状态的分类 四、有限马尔可夫链 五、状态的周期性 六、极限定理 七、生灭过…...

prometheus
文章目录 一、Prometheus简介什么是Prometheus?Prometheus的优势Prometheus的组件、架构Prometheus适用于什么场景Prometheus不适合什么场景 二、相关概念数据模型指标名称和标签样本表示方式 指标类型Counter计数器Gauge仪表盘Histogram直方图Summary摘要 Jobs和In…...
Vi 和 Vim 编辑器
Vi 和 Vim 编辑器 vi 和 vim 的基本介绍 Linux 系统会内置 vi 文本编辑器 Vim 具有程序编辑的能力,可以看做是 Vi 的增强版本,可以主动的以字体颜色辨别语法的正确性,方便程序设计。 代码补完、编译及错误跳转等方便编程的功能特别丰富&…...
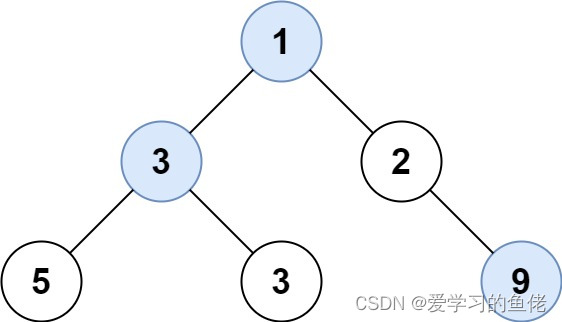
算法沉淀——队列+宽度优先搜索(BFS)(leetcode真题剖析)
算法沉淀——队列宽度优先搜索(BFS) 01.N 叉树的层序遍历02.二叉树的锯齿形层序遍历03.二叉树最大宽度04.在每个树行中找最大值 队列 宽度优先搜索算法(Queue BFS)是一种常用于图的遍历的算法,特别适用于求解最短路径…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
