C++动态规划-线性dp算法
莫愁千里路
自有到来风
CSDN 请求进入专栏 X
是否进入《C++专栏》?
确定
目录
线性dp简介
斐波那契数列模型
第N个泰波那契数
思路:
代码测试:
三步问题
思路:
代码测试:
最小花费爬楼梯
思路:
代码测试:
路径问题
数字三角形
思路:
代码测试:
不同路径
思路:
代码测试:
LIS模型
最长递增子序列
思路:
代码测试:
线性dp简介
线性DP(Introduction)
线性DP是动态规划问题中的一类问题,指状态之间有 线性关系 的动态规划问题
DP解题套路
<1>根据题意列出状态表示dp表里面的值所代表的含义
分析问题的过程中发现重复子问题
<2>根据状态表示列出状态转移方程dp[i]等于什么
<3>初始化填dp表的时候不能越界访问
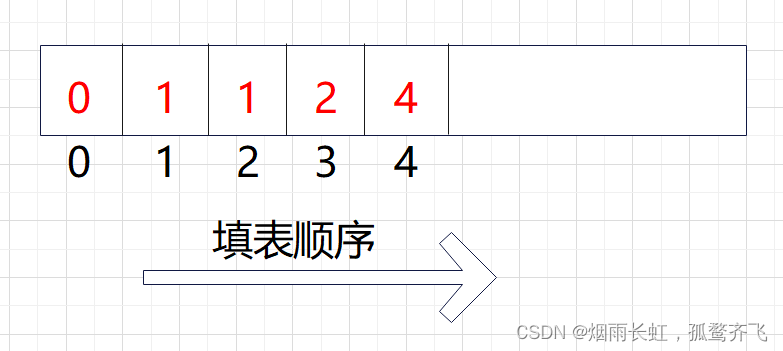
<4>填表顺序递推求解的顺序
斐波那契数列模型
第N个泰波那契数
题目链接:第N个泰波那契数
泰波那契序列 Tn 定义如下:
T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2
给你整数
n,请返回第 n 个泰波那契数 Tn 的值。示例 1:
输入:n = 4 输出:4 解释: T_3 = 0 + 1 + 1 = 2 T_4 = 1 + 1 + 2 = 4示例 2:
输入:n = 25 输出:1389537提示:
0 <= n <= 37- 答案保证是一个 32 位整数,即
answer <= 2^31 - 1
思路:
<1>状态表示 dp[i]表示第 i 个泰波那契数的值 <2>状态转移方程 dp[i] = dp[i-1] + dp[i-2] + dp[i-3] (Tn+3 = Tn + Tn+1 + Tn+2) <3>初始化 dp[0] = 0,dp[1] = dp[2] = 1 <4>填表顺序 从左至右
代码测试:
时间复杂度O(N)
空间复杂度O(N)
class Solution { public:int tribonacci(int n) {//防止数组越界if(n == 0) return 0;if(n == 1||n == 2) return 1;vector<int> dp(n+1);//初始化dp[0] = 0,dp[1] = dp[2] = 1;//顺序填表for(int i = 3;i<=n;i++)//状态转移方程dp[i] = dp[i-1]+dp[i-2]+dp[i-3];return dp[n];} };
三步问题
题目链接:三步问题
三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要对结果模1000000007。
示例1:
输入:n = 3 输出:4 说明: 有四种走法示例2:
输入:n = 5 输出:13提示:
- n范围在[1, 1000000]之间
思路:
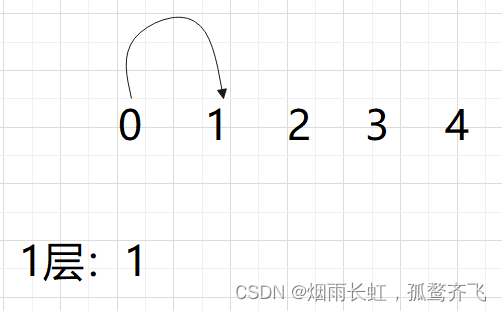
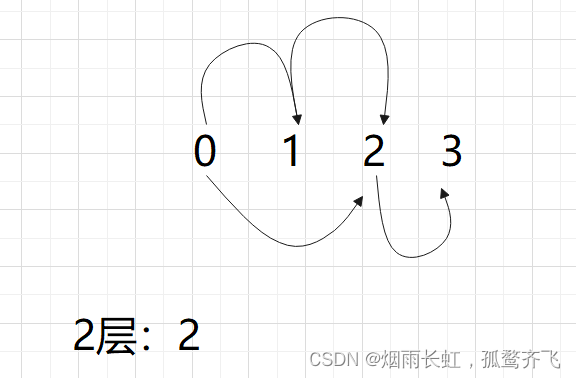
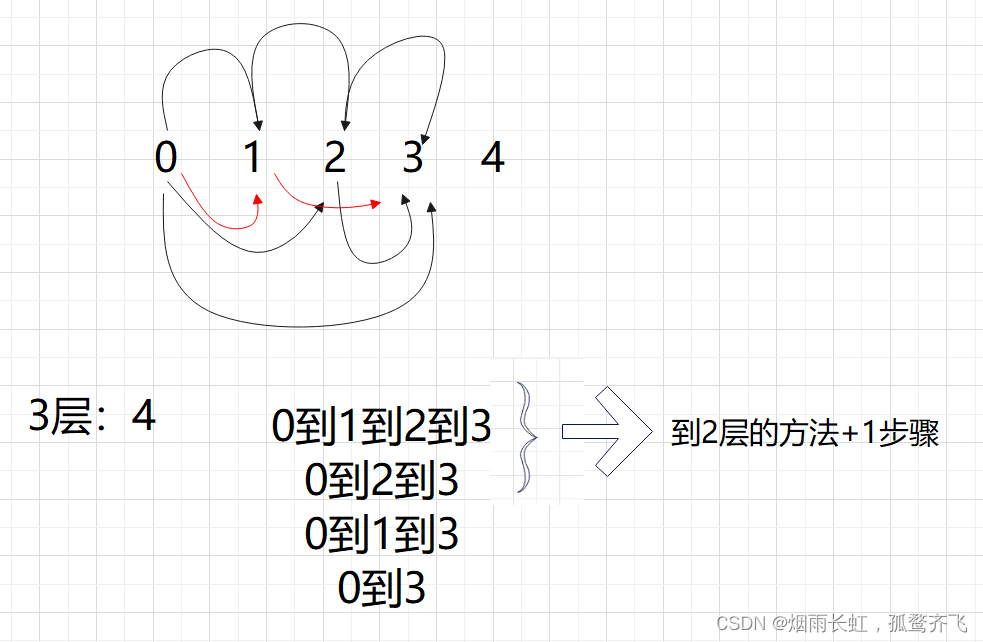
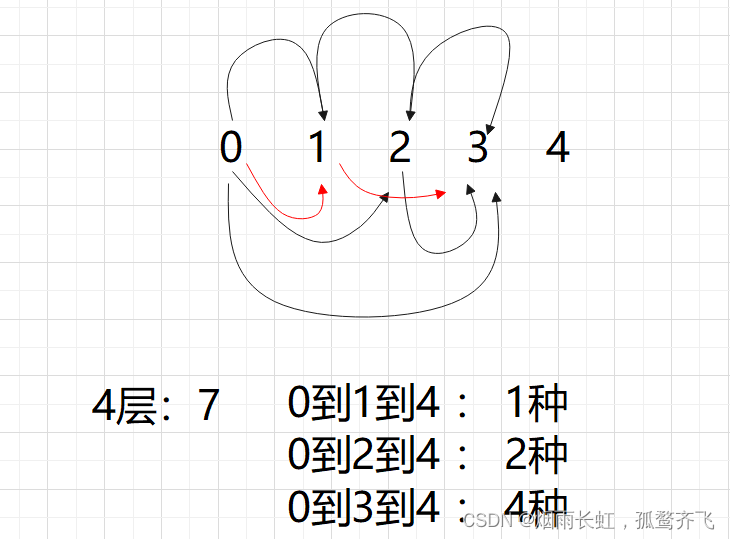
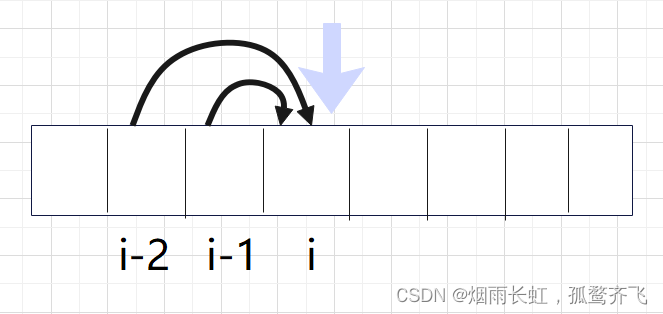
我们发现从 4 层开始就是前三项之和,第五层就是:7 + 4 + 2= 13
所以从第四层开始,满足斐波那契规律
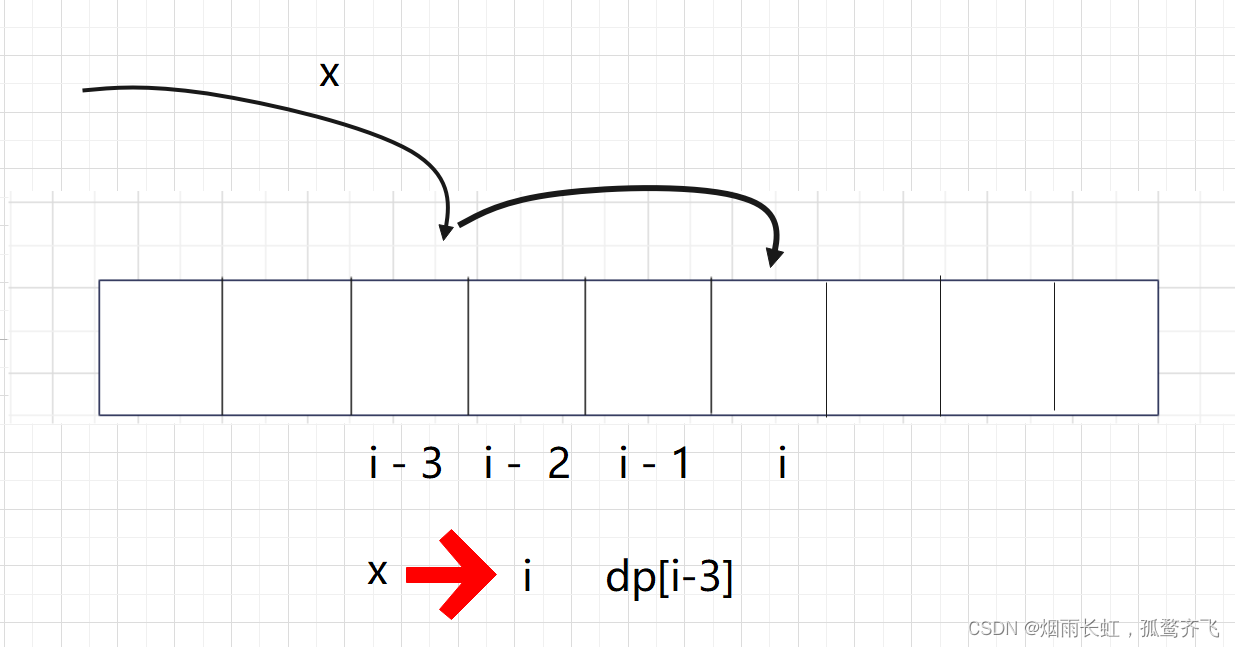
<1>状态表示 以 i 为结尾,dp[i]表示到达 i 位置时,一共有多少种方法 <2>状态转移方程 以 i 的位置的状态,最近的一步开始划分问题
从(i-1)到 i:dp[i-1]
从(i-2)到 i:dp[i-2]
从(i-3)到 i:dp[i-3]
dp[i] = dp[i-1]+dp[i-2]+dp[i-3]
<3>初始化 dp[1] = 1,dp[2] = 2,dp[3] = 4 <4>填表顺序 从左往右 代码测试:
时间复杂度O(N)
空间复杂度O(N)
class Solution { public:int waysToStep(int n) {//取模数据const int MOD = 1e9+7; //边界问题if(n == 1||n == 2) return n;if(n == 3) return 4;vector<int> dp(n+1);//初始化dp[1] = 1,dp[2] = 2,dp[3] = 4;//顺序填表for(int i = 4;i<=n;i++)//状态转移方程+取模操作dp[i] = ((dp[i-1]+dp[i-2])%MOD+dp[i-3])%MOD;return dp[n];} };
最小花费爬楼梯
题目链接:最小花费爬楼梯
数组的每个下标作为一个阶梯,第
i个阶梯对应着一个非负数的体力花费值cost[i](下标从0开始)。每当爬上一个阶梯都要花费对应的体力值,一旦支付了相应的体力值,就可以选择向上爬一个阶梯或者爬两个阶梯。
请找出达到楼层顶部的最低花费。在开始时,你可以选择从下标为 0 或 1 的元素作为初始阶梯。
示例 1:
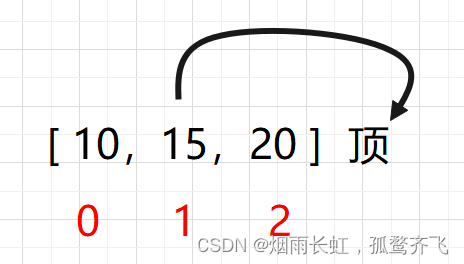
输入:cost = [10, 15, 20] 输出:15 解释:最低花费是从 cost[1] 开始,然后走两步即可到阶梯顶,一共花费 15 。示例 2:
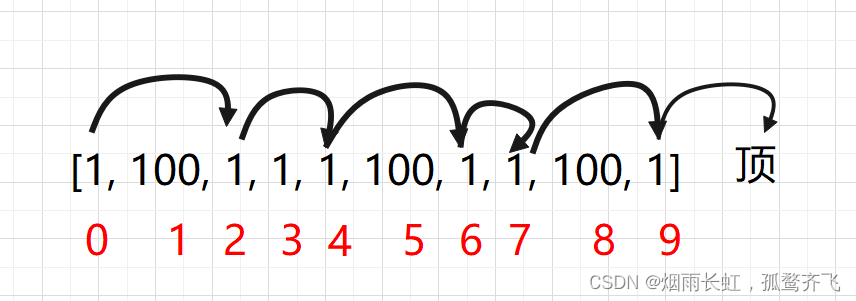
输入:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 输出:6 解释:最低花费方式是从 cost[0] 开始,逐个经过那些 1 ,跳过 cost[3] ,一共花费 6 。提示:
2 <= cost.length <= 10000 <= cost[i] <= 999
思路:
由题意可知:我们的楼层顶部并不是数组的末元素,而是末元素的下一位
<1>状态表示 以 i 为结尾,dp[i]表示到达 i 位置时,最小花费 <2>状态转移方程 使用之前或者之后的状态,推导出dp[i]的值
根据最近的一步来划分问题
(1)先到达 i-1 的位置,然后支付cost[i-1],走一步:dp[i-1]+cost[i-1]
(2)先到达 i-2 的位置,然后支付cost[i-2],走二步:dp[i-2]+cost[i-2]
dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
<3>初始化 由题意 你可以选择从下标为 0 或 1 的元素作为初始阶梯 得:
dp[0] = dp[1] = 0
<4>填表顺序 从左往右 <5>返回值 dp[n]
代码测试:
class Solution { public:int minCostClimbingStairs(vector<int>& cost) {//计算数组长度int n = cost.size();vector<int> dp(n+1);//初始化dp[0] = dp[1] = 0;//顺序填表for(int i = 2;i<=n;i++)//状态转移方程dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);return dp[n]; } };
路径问题
数字三角形
题目链接:数字三角形
题目描述#
观察下面的数字金字塔
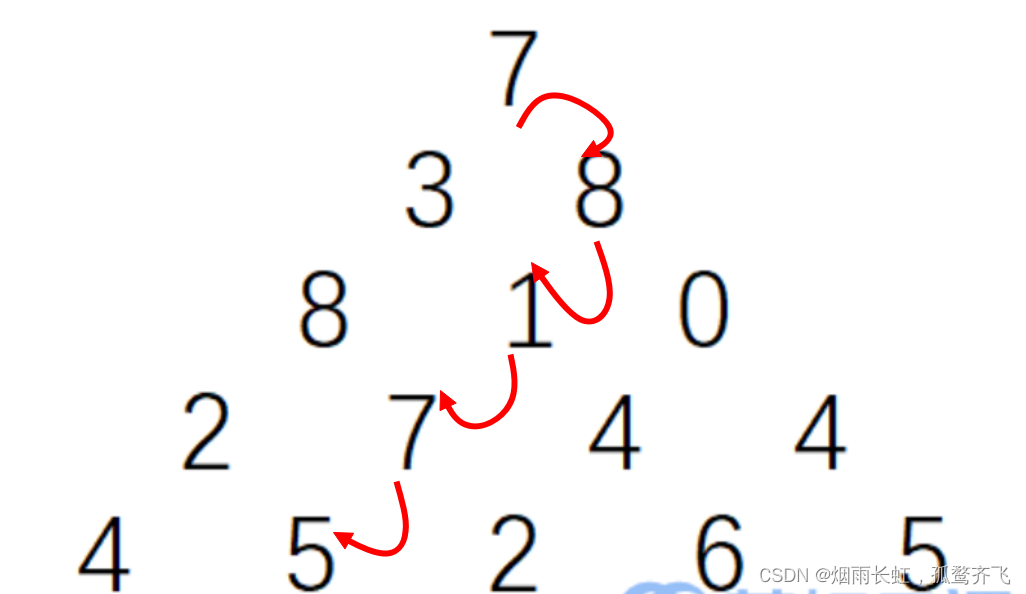
写一个程序来查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。
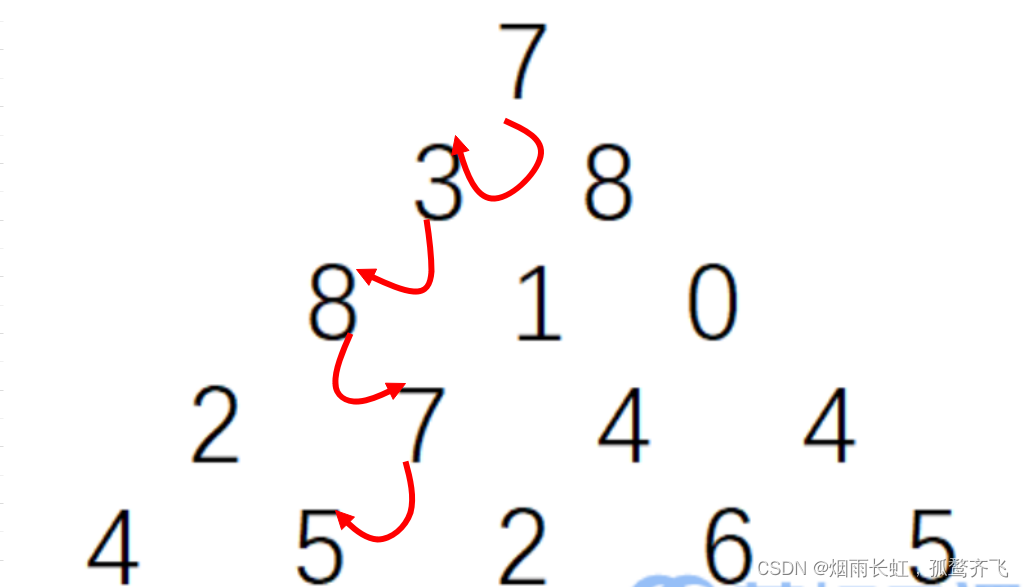
在上面的样例中,从 7→3→8→7→5 的路径产生了最大权值。
输入格式#
第一个行一个正整数 r 表示行的数目。
后面每行为这个数字金字塔特定行包含的整数。
输出格式#
单独的一行,包含那个可能得到的最大的和。
输入输出样例#
输入 #1
5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5输出 #1
30
思路:
在看到数字三角形的构造时,我们首先想到用 二维数组 来存放整个三角形(行与列)
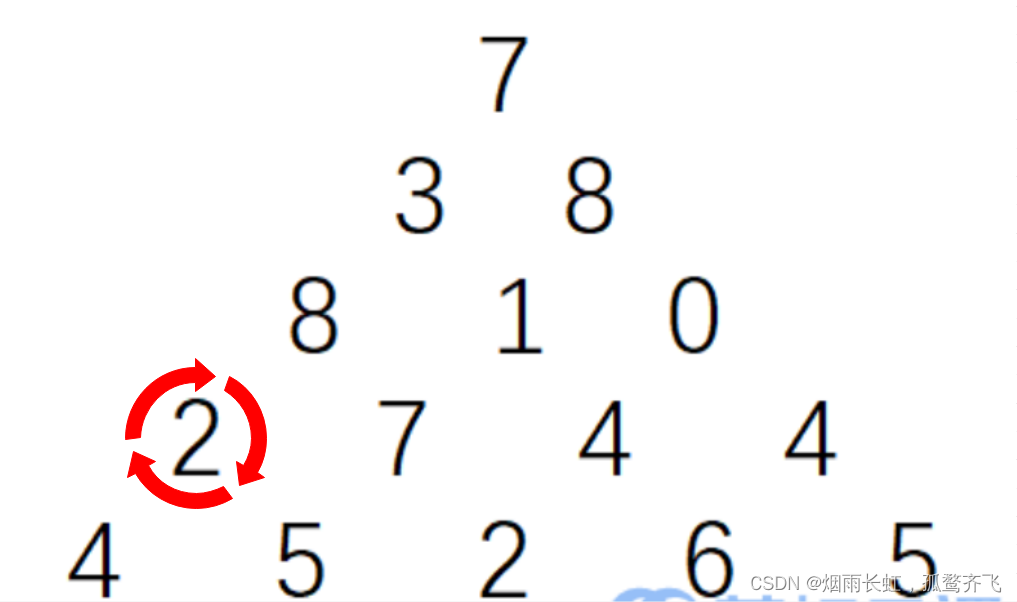
也许有人会想到 贪心算法 来实现,但是贪心算法在这里是不适用的
贪心只注重眼前的利益(如上图),贪心策略算出的数字的和是:28 不符合我们的最大值
所以眼光放长,我们要的是最后的数字和最大,尝试用 动态规划 解决问题
注意:
我们发现从上面往下一步步走很麻烦,直接搜索肯定超时
所以我们的切入点是 由下至上 的回溯,依层次更换改动大值,回到顶端时,就是结果
例如:
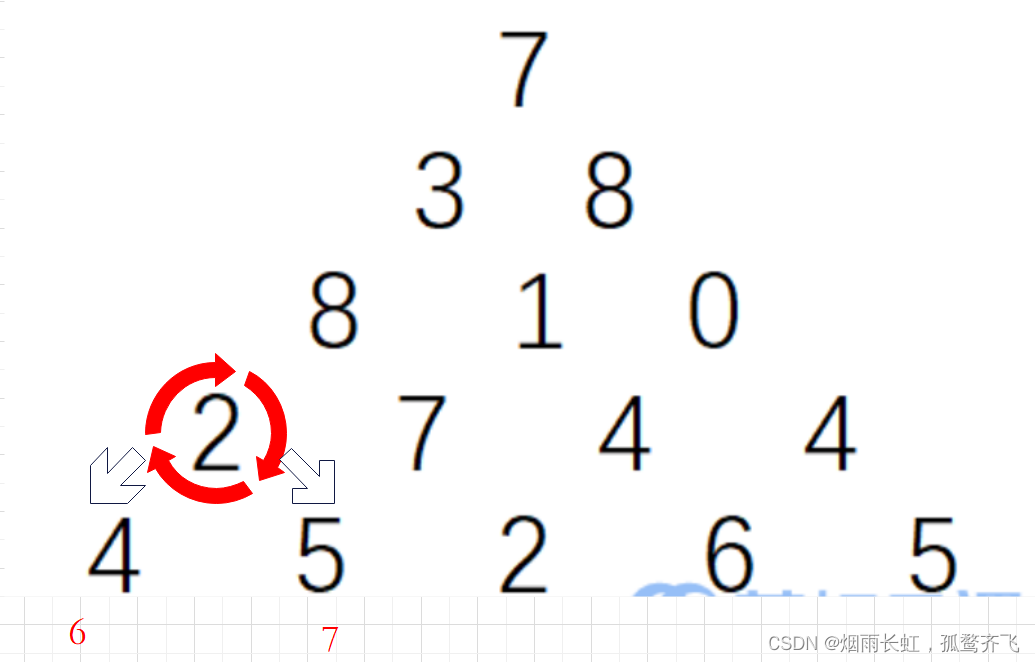
我们找到倒数第二排的元素 2 ,此时只有两种方法可以走,左下方或者右下方
我们要保证数字和最大,所以必然选择 右下方 ,这个时候的较大值为 7
同理:我们考虑倒数第二排的元素 7 ,较大值为 12
依次类推则倒数第二排变为:
7 12 10 10因为我们的倒数第二排已经包含了最后一排的最优解,所以我们的三角形可以简化成:
7 3 8 8 1 0 7 12 10 10方法同上我们找到倒数第二排的元素 8 ,再比较走两条路的值,右边的值更大,选择右边的值,所以这个时候的较大值为 20
以此类推,得到下面的数字三角形:
7 3 8 20 13 107 23 2130 23 21 20 13 10 7 12 10 10 4 5 2 6 5最后得到我们的最大数字之和为 30
所以我们的最佳路径是:7→3→8→7→5
思路我们已经理清了,接下来开始推导我们的状态转移方程:
<1>状态表示 以 [i,j] 为结尾,dp[ i ][ j ]表示到达 [i,j] 位置时,最大的数字之和 <2>状态转移方程 dp[i][j]+=max(dp[i+1][j],dp[i+1][j+1])
<3>初始化 按要求输入
<4>填表顺序 从下至上,从左至右 <5>返回值 dp[1][1] <6>小总结 画图求解,发现规律,列出状态转移方程
代码测试:
#include<bits/stdc++.h> using namespace std; int main() {int n = 0;cin>>n;vector<vector<int>> dp((n+1),vector<int>(n+1));//初始化for(int i = 1;i<=n;i++)for(int j = 1;j<=i;j++)cin>>dp[i][j];//顺序填表for(int i = n-1;i>=1;i--)for(int j = 1;j<=i;j++)//状态转移方程dp[i][j]+=max(dp[i+1][j],dp[i+1][j+1]);//返回值cout<<dp[1][1]<<endl;return 0; }
不同路径
题目链接:不同的路径
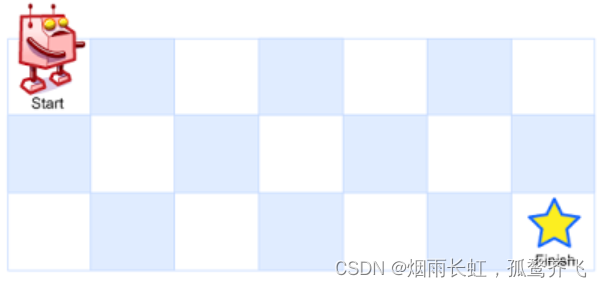
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角
(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7 输出:28示例 2:
输入:m = 3, n = 2 输出:3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下示例 3:
输入:m = 7, n = 3 输出:28示例 4:
输入:m = 3, n = 3 输出:6提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 10^9
思路:
二维dp
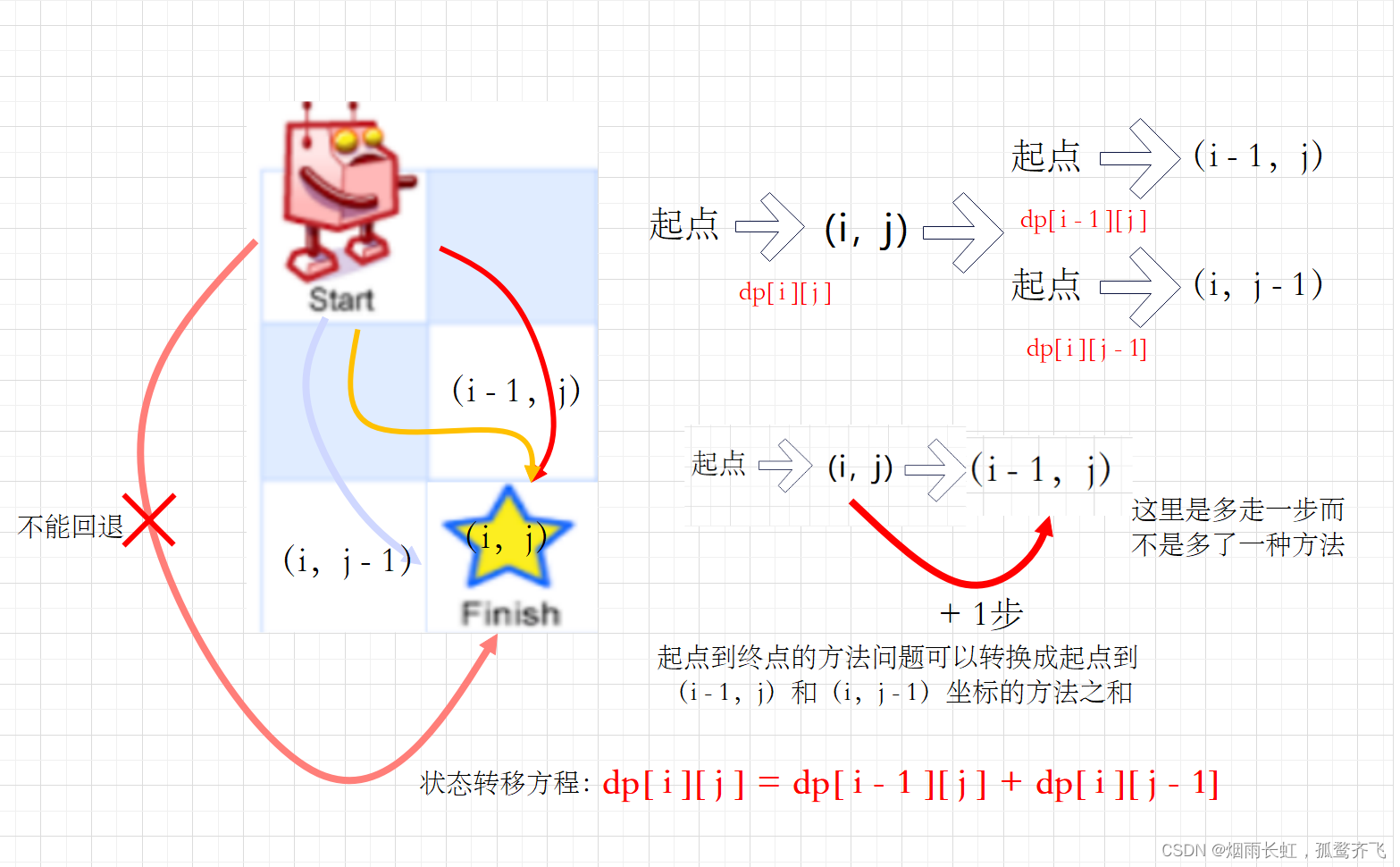
状态转移方程的得出
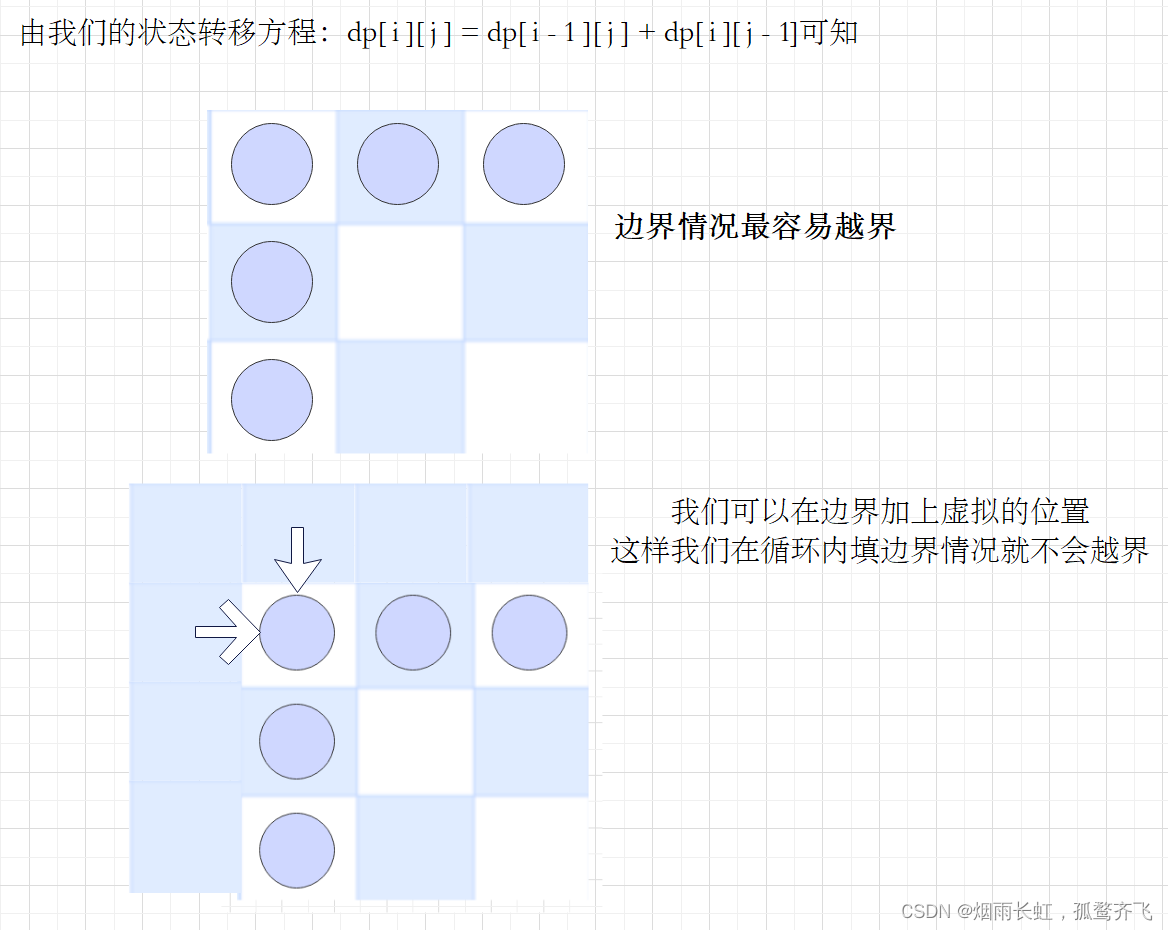
初始化问题
为了防止数组越界,所以我们要考虑 dp 的初始化问题
注意:
<1>然后在考虑虚拟位置的值,要保证我们后面填表的结果是正确的
<2>二维数组的行和列都要加一(加上了虚拟位置)
我们只要将 dp[0][1] 或者 dp[0][1] 的位置初始化为 1 就可以了
<1>状态表示 以[i,j]为结尾时,dp[i][j]表示走到[i,j]的位置,一共有多少种方式 <2>状态转移方程 dp[ i ][ j ] = dp[ i - 1 ][ j ] + dp[ i ][ j - 1]
<3>初始化 dp[0][1] = 1 <4>填表顺序 从左至右,从上至下 <5>返回值 dp[m][n] 代码测试:
class Solution { public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m+1,vector<int>(n+1));//初始化dp[0][1] = 1;//顺序填表for(int i = 1;i<=m;i++)for(int j = 1;j<=n;j++)//状态转移方程dp[i][j] = dp[i-1][j]+ dp[i][j-1];//返回值return dp[m][n];} };
LIS模型
最长递增子序列
题目链接:最长递增子序列
给你一个整数数组
nums,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,
[3,6,2,7]是数组[0,3,1,6,2,2,7]的子序列。示例 1:
输入:nums = [10,9,2,5,3,7,101,18] 输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。示例 2:
输入:nums = [0,1,0,3,2,3] 输出:4示例 3:
输入:nums = [7,7,7,7,7,7,7] 输出:1
思路:
子序列的介绍:
子序列指的是一个序列中,按照原顺序选出若干个 一定连续 的元素所组成的序列
状态转移方程的推理:
初始化:将dp标准的状态成最坏的情况,最后更新dp表就可以了
填表顺序:因为我们要填 dp[i] 就要用到前面的值,所以是:从左往右
注意:要判断 nums[j]<nums[i]
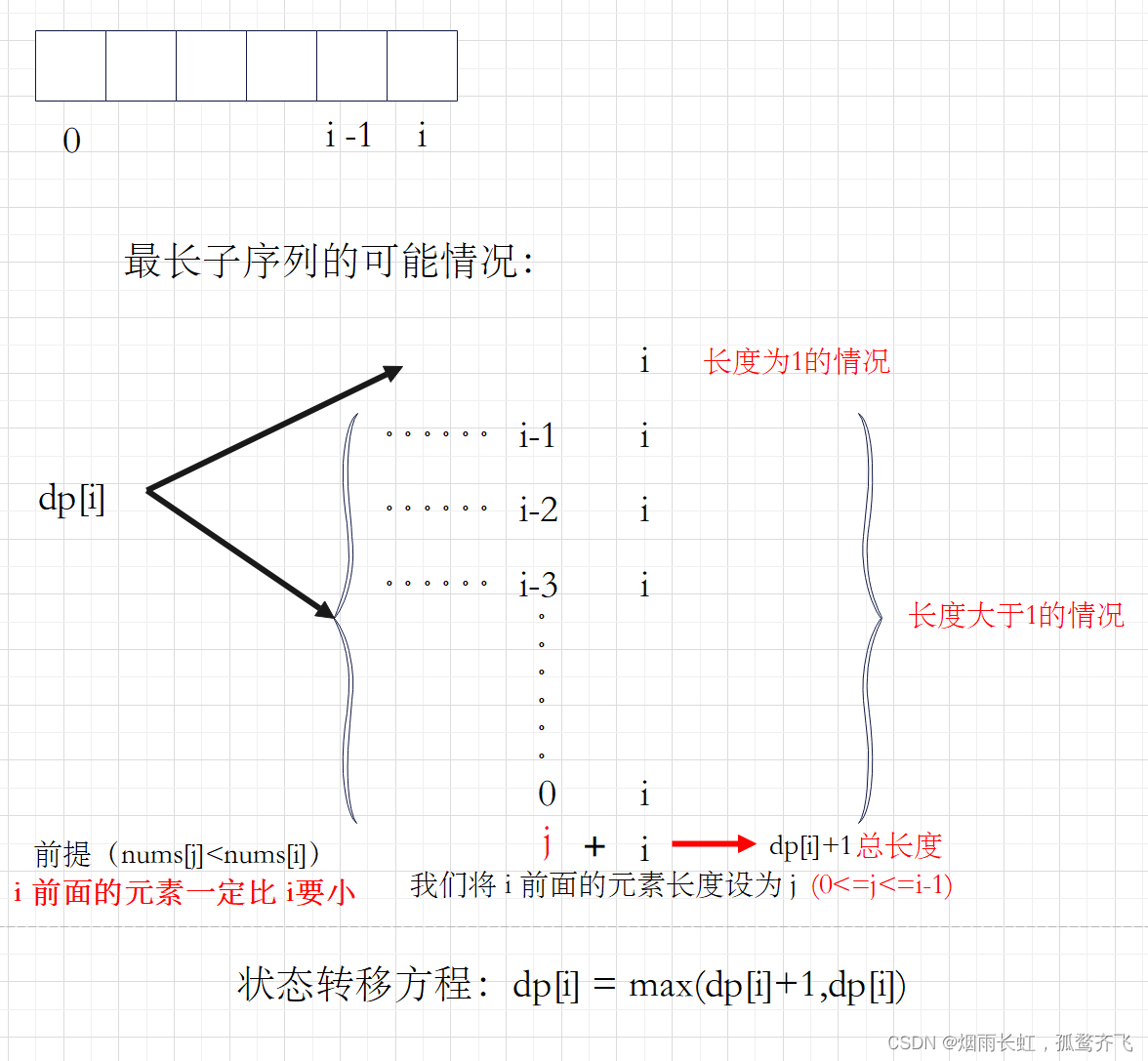
<1>状态表示 dp[i]表示以 i 位置为结尾的所有子序列中,最长递增子序列的长度 <2>状态转移方程 dp[i] = max(dp[i]+1,dp[i])
<3>初始化 dp表中所有元素都置为1 <4>填表顺序 从左往右 <5>返回值 dp表中的最大值 代码测试:
class Solution { public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();//初始化vector<int> dp(n,1);int ret = 1;//顺序填表for(int i = 1;i<n;i++){for(int j = 0;j<i;j++)//前提条件if(nums[j]<nums[i])//状态转移方程dp[i] = max(dp[j]+1,dp[i]);ret = max(ret,dp[i]);}//返回值return ret;} };
相关文章:
C++动态规划-线性dp算法
莫愁千里路 自有到来风 CSDN 请求进入专栏 X 是否进入《C专栏》? 确定 目录 线性dp简介 斐波那契数列模型 第N个泰波那契数 思路: 代码测试: 三步问题 思路: 代码测试: 最小花费爬楼梯 思路…...
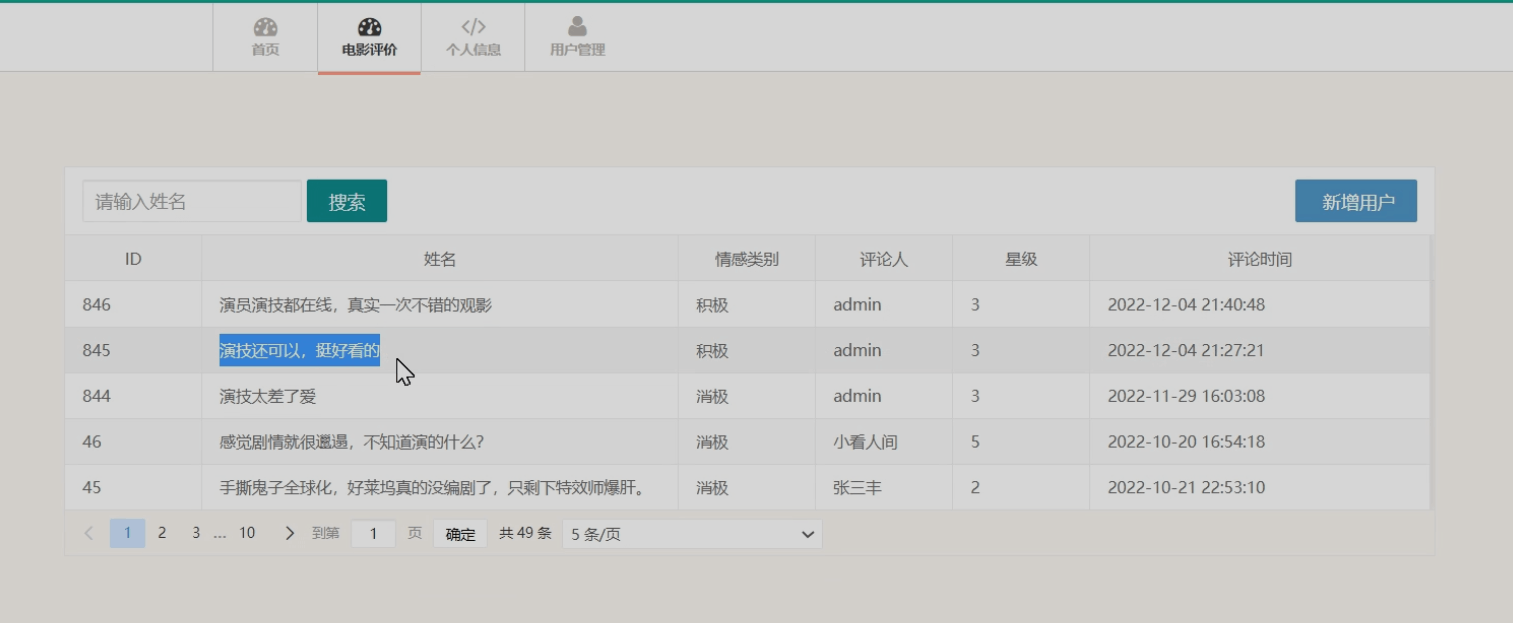
基于 Python 深度学习的电影评论情感分析系统,附源码
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12W、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...
如何查看Apple Watch的步数?这里提供几个方法
所有Apple Watch都配有内置计步器,即具有步进跟踪功能。当你第一次设置手表时,你的Apple Watch将自动开始计算步数。让我们看看如何在Apple Watch上查看步数。 使用活动应用程序 1、按下Apple Watch上的数字皇冠,打开应用程序屏幕。 2、点击活动应用程序。 3、你会看到…...
解决‘vue‘ 不是内部或外部命令,也不是可运行的程序(设置全局变量)
发现是没有执行: npm install -g vue/cli 但是发现还是不行 此时,我们安装了 Vue CLI,但是在运行 vue ui 命令时出现了问题。这通常是因为全局安装的 Vue CLI 的路径没有被正确地添加到系统的环境变量中。 可以尝试以下几种方法来解决这个问…...
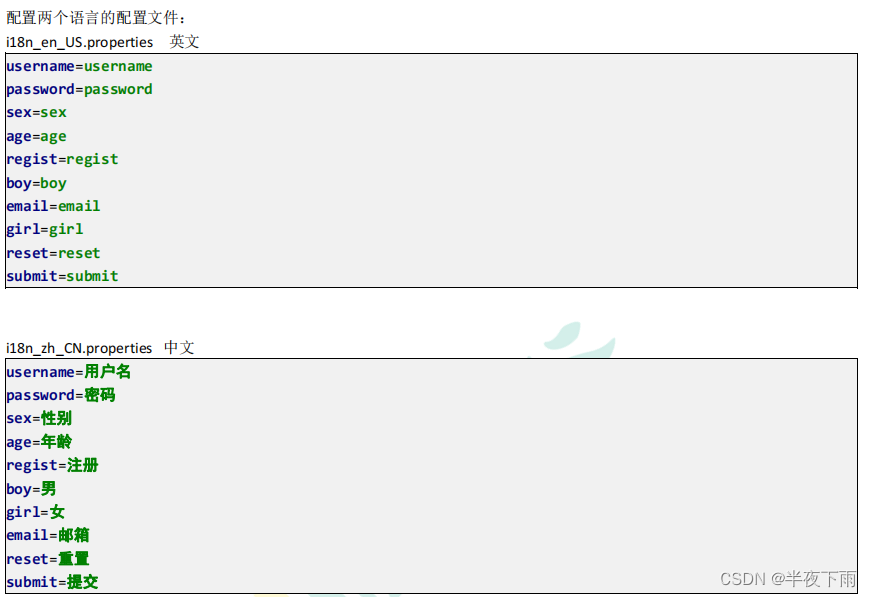
JavaWeb学习|i18n
学习材料声明 所有知识点都来自互联网,进行总结和梳理,侵权必删。 引用来源:尚硅谷最新版JavaWeb全套教程,java web零基础入门完整版 i18n 国际化(Internationalization)指的是同一个网站可以支持多种不同的语言&…...

数据库日志已经很大了,比如200多G,不能收缩到几兆,实际操作过只能到30G
当数据库日志文件(通常称为事务日志或事务日志文件)变得非常大时,确实可能会遇到问题,因为这会占用大量的磁盘空间,并可能影响数据库的性能。收缩日志文件到非常小的大小(例如从200多G到几兆)可…...
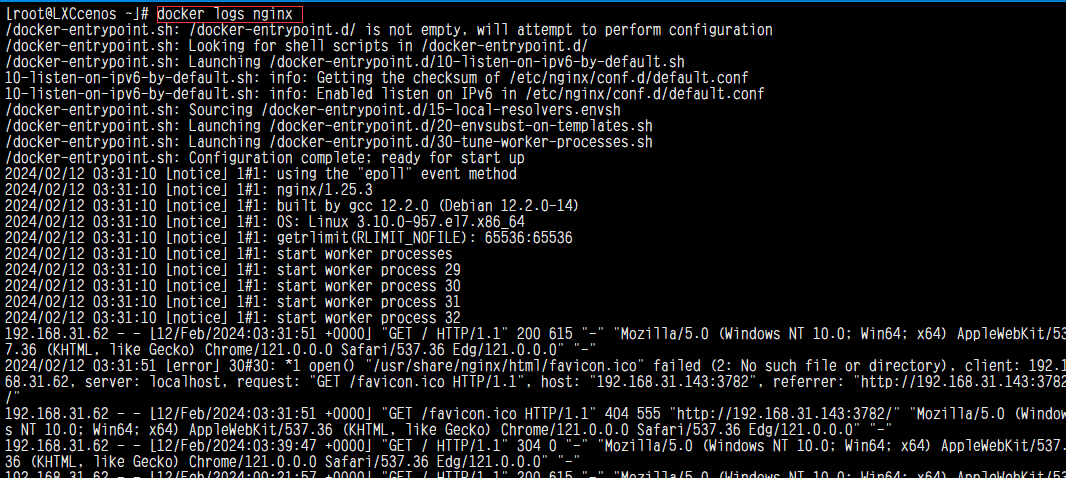
docker常用容器命令
首先说下容器: 它是指当docker运行镜像时,创建了一个隔离环境,称之为 容器。 这种方式优点:可以开启多个服务,服务之前是互相隔离的(比如:在一台服务器上可以开启多个mysql,可以是…...
2022省赛真题:冬奥大抽奖)
蓝桥杯(Web大学组)2022省赛真题:冬奥大抽奖
思路: 使用模板字符串,借助time的值选择添加或移除样式的盒子,由于盒子的类名最多为li9,所以要将time的值取余,且判断余数为0时,就取1,否则会获取空值报错 .ul .li${time%9!0?time%9:1} 代码…...

单调队列 单调栈
单调队列 一种下标单调,值也单调的队列。 以长度为 k k k 的区间内最大值为例,在一个数进队时,可以知道在他之前的肯定下标比他小,所以如果前面的数比他小,那么前面的数肯定不能成为最大值,直接出队,如果前面的数比他大,因为前面的数下标靠前,所以这个数有可能在以…...

Java基础-泛型
泛型: 泛型,就是允许在定义类、接口时通过一个标识表示类中某个属性的类型或者是某个方法的返回值或参数的类型。这个类型参数将在使用时(例如,继承或实现这个接口、创建对象或调用方法时)确定(即传入实际的…...

Vue 全组件 局部组件
一、组件定义和使用 1、全局组件 定义 <template> <div> <h1>This is a global component</h1> </div> </template> <script lang"ts"> </script> <style></style> 导入 全局组件在main.tsÿ…...
几个经典金融理论
完整EA:Nerve Knife.ex4黄金交易策略_黄金趋势ea-CSDN博客 一、预期效用理论 预期效用理论是描述人们在做出决策时如何考虑风险和不确定性的一种理论。该理论最初由经济学家冯诺伊曼(John von Neumann)和奥斯卡摩根斯坦恩(Oskar…...

c++语言max函数的使用
目录 头文件包含 使用语法 注意事项 头文件包含 首先,在使用std::max函数之前,需要包含头文件 <algorithm>。 #include <algorithm> 使用语法 std::max函数有两种重载形式,一种用于比较两个值,另一种用于比较多…...
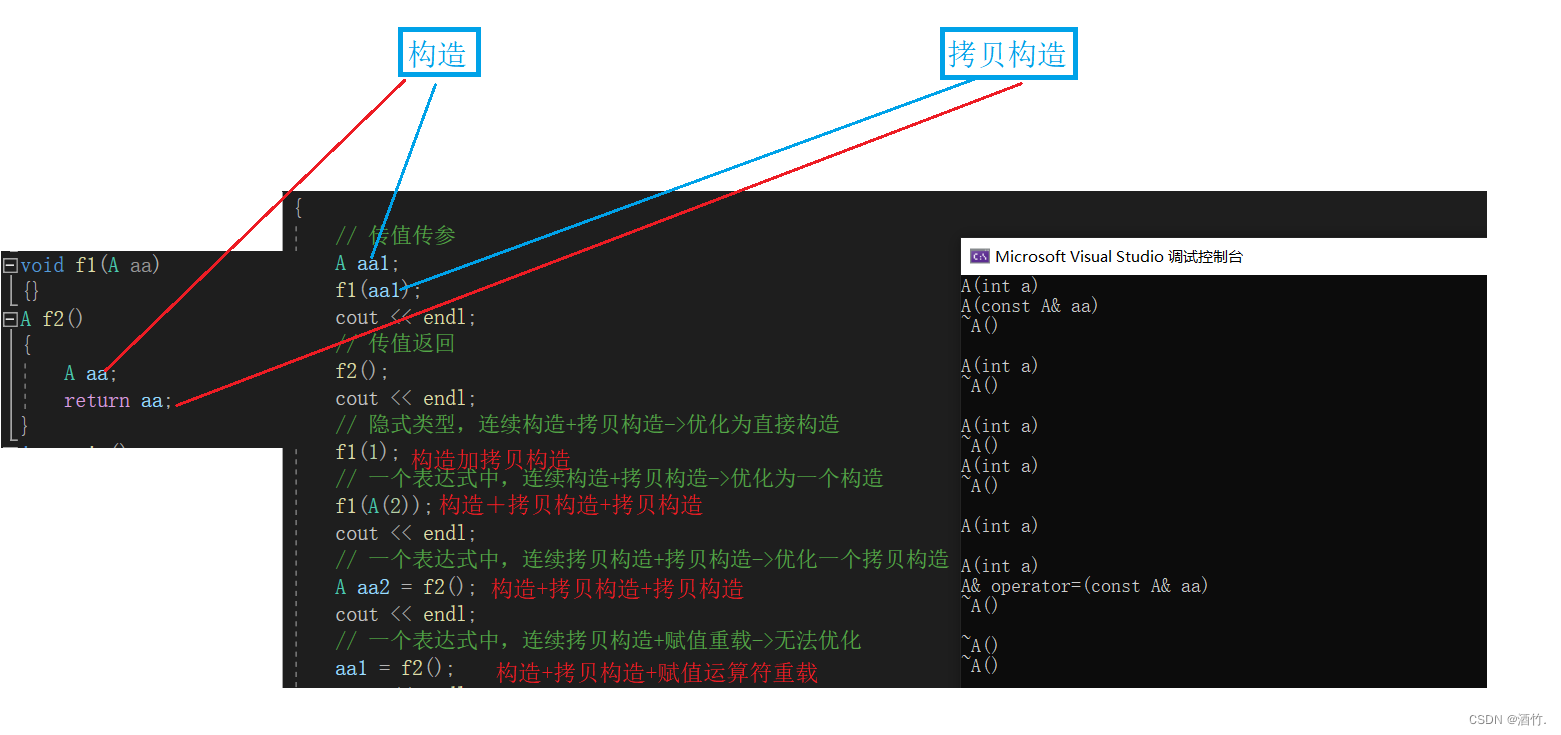
c++阶梯之类与对象(下)
前文: c阶梯之类与对象(上)-CSDN博客 c阶梯之类与对象(中)-CSDN博客 c阶梯之类与对象(中)< 续集 >-CSDN博客 1. 再谈构造函数 1.1 构造函数体赋值 在创建对象时&a…...
机器学习--K-近邻算法常见的几种距离算法详解
文章目录 距离度量1 欧式距离(Euclidean Distance)2 曼哈顿距离(Manhattan Distance)3 切比雪夫距离 (Chebyshev Distance)4 闵可夫斯基距离(Minkowski Distance)5 标准化欧氏距离 (Standardized EuclideanDistance)6 余弦距离(Cosine Distance)7 汉明距离(Hamming Distance)【…...
常用术语整理》)
<网络安全>《30 网络信息安全基础(1)常用术语整理》
1 肉鸡 所谓“肉鸡”是一种很形象的比喻,比喻那些可以随意被我们控制的电脑,对方可以是WINDOWS系统,也可以是UNIX/LINUX系统,可以是普通的个人电脑,也可以是大型的服务器,我们可以象操作自己的电脑那样来操…...
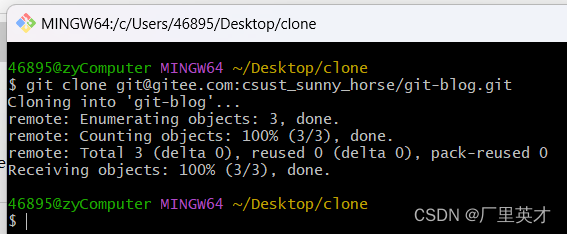
Git远程仓库的使用(Gitee)及相关指令
目录 1 远程仓库的创建和配置 1.1 创建远程仓库 1.2 设置SSH公钥 2 指令 2.1 git remote add 远端名称(一般为origin) 仓库路径 2.2 git remote 2.3 git push [-f] [--set-upstream] [远端名称 [本地分支名][:远端分支名]] 2.3 git clone url 2.4 git fetch 2.5 git p…...
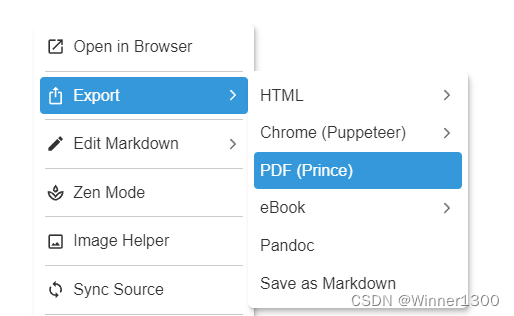
vscode +markdown 的安装和使用
文章目录 前言一、vscode markdown 是什么?1.vscode是什么?2.markdown 是什么? 二、安装步骤1.下载2.安装 三、安装插件1.安装 Markdown All in One2.安装 Markdown Preview Enhanced3. Paste Image v1.0.44.LimfxCodeExv0.7.105.Code Spell …...
Python爬虫之自动化测试Selenium#7
爬虫专栏:http://t.csdnimg.cn/WfCSx 前言 在前一章中,我们了解了 Ajax 的分析和抓取方式,这其实也是 JavaScript 动态渲染的页面的一种情形,通过直接分析 Ajax,我们仍然可以借助 requests 或 urllib 来实现数据爬取…...

快速学习Spring
Spring 简介 Spring 是一个开源的轻量级、非侵入式的 JavaEE 框架,它为企业级 Java 应用提供了全面的基础设施支持。Spring 的设计目标是简化企业应用的开发,并解决 Java 开发中常见的复杂性和低效率问题。 Spring常用依赖 <dependencies><!-…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...