排序算法---计数排序
原创不易,转载请注明出处。欢迎点赞收藏~
计数排序(Counting Sort)是一种线性时间复杂度的排序算法,其核心思想是通过统计待排序元素的个数来确定元素的相对位置,从而实现排序。
具体的计数排序算法步骤如下:
1. 找出待排序数组中的最大值,并创建一个统计数组count[],其长度为最大值加1。
2. 遍历待排序数组,统计每个元素出现的次数,将统计结果存储在count[]数组中。count[i]表示元素i出现的次数。
3. 对count[]数组进行累加,得到每个元素在排序后的数组中的最后一个位置。即count[i]表示小于等于元素i的元素个数。
4. 创建一个临时数组temp[],其长度与待排序数组相同。
5. 逆序遍历待排序数组,根据count[]数组中的记录,将每个元素放入temp[]数组中的正确位置。
6. 将temp[]数组的元素复制回待排序数组,完成排序。
计数排序的时间复杂度为O(n+k),其中n是待排序数组的长度,k是待排序数组中的最大值。由于需要创建额外的count[]和temp[]数组,所以空间复杂度为O(n+k)。
需要注意的是,计数排序适用于元素范围较小且非负整数的排序,如果待排序数组包含负数或者小数,则需要进行适当的转换或调整。计数排序是稳定的排序算法,因为相同元素的相对顺序在排序后保持不变,但它不是基于比较的排序算法,因此在某些情况下比其他排序算法更高效。
下面是一个使用C语言实现的计数排序示例:
#include <stdio.h>void counting_sort(int arr[], int n)
{int max = arr[0];// 找出最大值for (int i = 1; i < n; i++){if (arr[i] > max){max = arr[i];}}// 创建统计数组count[],并初始化为0int count[max + 1];for (int i = 0; i <= max; i++){count[i] = 0;}// 统计每个元素的次数for (int i = 0; i < n; i++){count[arr[i]]++;}// 累加count[]数组,表示小于等于元素i的元素个数for (int i = 1; i <= max; i++){count[i] += count[i - 1];}// 创建临时数组temp[],存储排好序的元素int temp[n];// 根据count[]数组中的记录,将元素放入temp[]数组的正确位置for (int i = n - 1; i >= 0; i--){temp[count[arr[i]] - 1] = arr[i];count[arr[i]]--;}// 将temp[]数组的元素复制回原数组arr[]for (int i = 0; i < n; i++){arr[i] = temp[i];}
}int main()
{int arr[] = {9, 3, 6, 1, 3, 2, 9, 0};int n = sizeof(arr) / sizeof(arr[0]);printf("排序前的数组:\n");for (int i = 0; i < n; i++){printf("%d ", arr[i]);}counting_sort(arr, n);printf("\n排序后的数组: \n");for (int i = 0; i < n; i++){printf("%d ", arr[i]);}putchar('\n');return 0;
}
这段代码实现了计数排序算法。主要包括以下步骤:
1.遍历数组找出最大值,确定统计数组count[]的长度。
2.创建并初始化统计数组count[],长度为最大值加1。
3.遍历数组,统计每个元素的出现次数,存储在count[]中。
4.累加count[]数组,表示小于等于元素i的元素个数。
5.创建临时数组temp[],用于存储排好序的元素。
6.逆序遍历原数组,根据count[]数组中的记录,将元素放入temp[]数组的正确位置。
7.将temp[]数组的元素复制回原数组arr[],完成排序。
运行如上代码,你可以看到以下输出:

相关文章:

排序算法---计数排序
原创不易,转载请注明出处。欢迎点赞收藏~ 计数排序(Counting Sort)是一种线性时间复杂度的排序算法,其核心思想是通过统计待排序元素的个数来确定元素的相对位置,从而实现排序。 具体的计数排序算法步骤如下ÿ…...

STM32——LCD(1)认识
目录 一、初识LCD 1. LCD介绍 2. 显示器的分类 3. 像素 4. LED和OLED显示器 5. 显示器的基本参数 (1)像素 (2)分辨率 (3)色彩深度 (4)显示器尺寸 (5ÿ…...
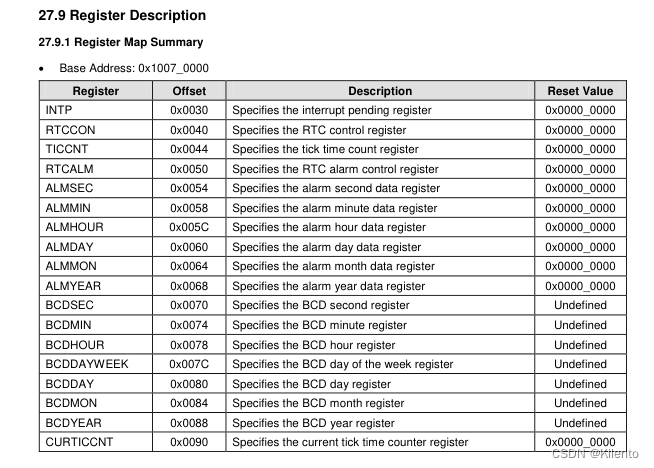
iTop-4412 裸机程序(二十二)- RTC时钟
目录 0.源码1. RTC2. iTop4412 中的 RTC使用的相关寄存器3. BCD编码4. 关键源码 0.源码 GitHub:https://github.com/Kilento/4412NoOS 1. RTC RTC是实时时钟(Real Time Clock)的缩写,是一种用于计算机系统的硬件设备࿰…...

Kafka 之 AdminClient API
目录 一. 前言 二. KafkaAdminClient API 2.1. API 总览 2.2. Topic 操作 2.2.1. 创建 Topic 2.2.2. Topic 列表 2.2.3. 删除 Topic 2.2.4. 描述 Topic 详细信息 2.3. 分区 Partition 操作 2.3.1. 增加分区 2.3.2. 分区副本重新分配 2.3.3. 查询分区副本列表 2.4.…...

Flutter run 一直 Running Gradle task ‘assembleDebug’…
发生缘由 Flutter 项目引入 fluttertoast 插件后,执行 Flutter run 一直 Running Gradle task ‘assembleDebug’…,最后发现下载 kotlin-compiler-embeddable-7.1.0.jar 特别的缓慢。 运行环境 电脑系统版本:Windows 10 64bit VS Code&…...
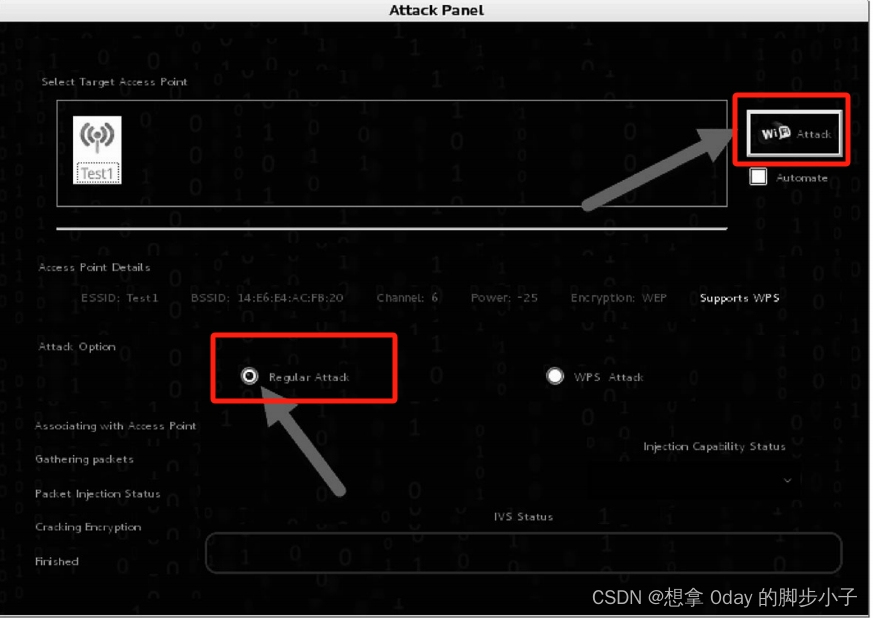
kali无线渗透之用wps加密模式破解出wpa模式的密码12
WPS(Wi-Fi Protected Setup,Wi-Fi保护设置)是由Wi-Fi联盟推出的全新Wi-Fi安全防护设定标准。该标准推出的主要原因是为了解决长久以来无线网络加密认证设定的步骤过于繁杂之弊病,使用者往往会因为步骤太过麻烦,以致干脆不做任何加密安全设定&…...

【Python】高级数据类型
🚩 WRITE IN FRONT 🚩 🔎 介绍:"謓泽"正在路上朝着"攻城狮"方向"前进四" 🔎🏅 荣誉:2021|2022年度博客之星物联网与嵌入式开发TOP5|TOP4、2021|2222年获评…...

挑战杯 python区块链实现 - proof of work工作量证明共识算法
文章目录 0 前言1 区块链基础1.1 比特币内部结构1.2 实现的区块链数据结构1.3 注意点1.4 区块链的核心-工作量证明算法1.4.1 拜占庭将军问题1.4.2 解决办法1.4.3 代码实现 2 快速实现一个区块链2.1 什么是区块链2.2 一个完整的快包含什么2.3 什么是挖矿2.4 工作量证明算法&…...

如何给最小化安装的CentOS主机装个远程桌面?
正文共:888 字 18 图,预估阅读时间:1 分钟 前面我们领微软云Azure的免费主机时(白嫖党618福利!来Azure领200美刀!外加云主机免费用一年!),发现“有资格免费试用服务”的主…...

知识图谱:py2neo将csv文件导入neo4j
文章目录 安装py2neo创建节点-连线关系图导入csv文件删除重复节点并连接边 安装py2neo 安装python中的neo4j操作库:pip install py2neo 安装py2neo后我们可以使用其中的函数对neo4j进行操作。 图数据库Neo4j中最重要的就是结点和边(关系)&a…...

备战蓝桥杯---图论之最短路Bellman-Ford算法及优化
目录 上次我们讲到复杂度为(nm)logm(m为边,n为点)的迪杰斯特拉算法,其中有一个明显的不足就是它无法解决包含负权边的图。 于是我们引进Bellman-Ford算法。 核心:枚举所有的点,能松弛就松弛,直…...

C++ //练习 5.19 编写一段程序,使用do while循环重复地执行下述任务:首先提示用户输入两个string对象,然后挑出较短的那个并输出它。
C Primer(第5版) 练习 5.19 练习 5.19 编写一段程序,使用do while循环重复地执行下述任务:首先提示用户输入两个string对象,然后挑出较短的那个并输出它。 环境:Linux Ubuntu(云服务器&#x…...
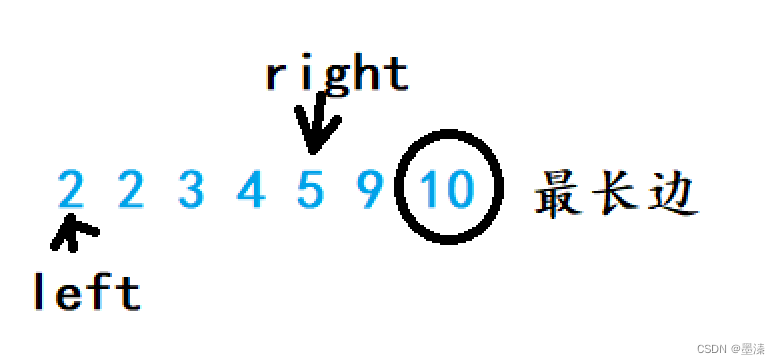
算法刷题:有效三角形个数
有效三角形个数 .题目链接题目详情算法原理补充知识点双指针:对撞指针 我的答案 . 题目链接 有效三角形个数 题目详情 算法原理 补充知识点 有效三角形需要满足的条件: ab>cac>bbc>a 其实在满足1的时候,c是最大的,那么2和3是显然成立的,因此我们可以这样解题: 对…...

python---变量
1.变量就是存储数据的空间,在内存上; 2.变量命名规则:(1)由数字,字母,下划线组成,数字不能开头; (2)不能和关键字冲突; (…...
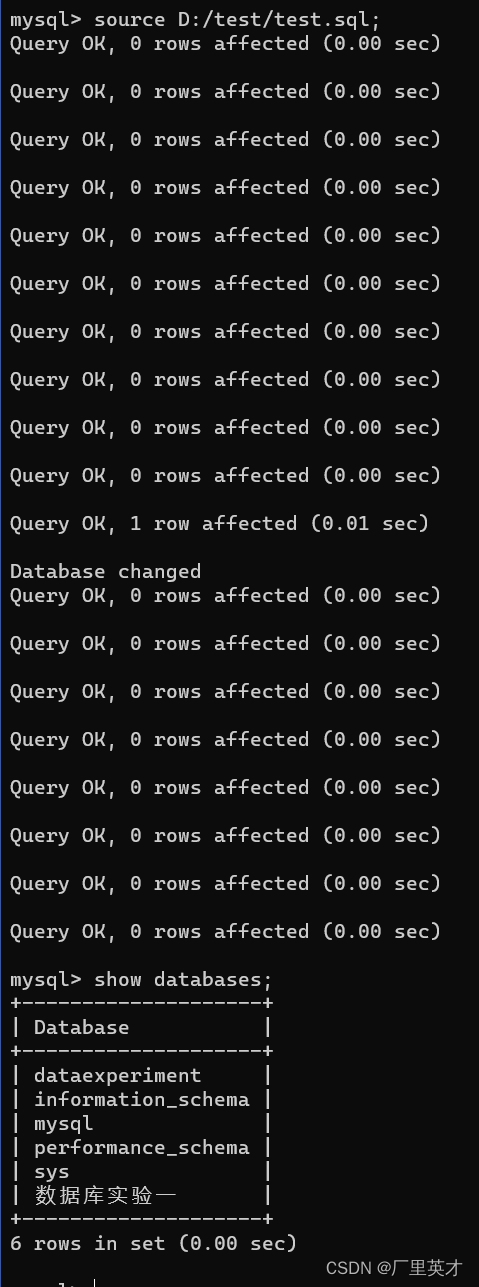
数据库第二次实验
目录 1 实验内容 2 SQL代码及运行截图 2.1 创建表并插入数据 2.1.1 创建表 2.1.2 插入数据 2.1.3 运行截图 2.2 修改表 2.2.1 SQL代码 2.2.2 运行截图 2.3 删除操作 2.3.1 SQL代码 2.3.2 运行截图 2.4 数据库的备份 2.5 数据库的恢复 1 实验内容 实验目的&#…...

容器高级知识:Kubernetes Pod 适配器模式详解
Kubernetes Pod 适配器(Adapter)模式详解 Kubernetes Pod 适配器模式是侧车(Sidecar)模式的一个特例,其中使用专用的 适配器容器 在主应用程序容器和其他服务或客户端之间 翻译 数据或信号。它充当桥梁,调整通信格式或协议以实现…...

云原生容器化-5 Docker常见操作命令
1.登录和退出docker仓库 使用docker login和docker logout分别用于登录和退出docker仓库。 #登录时携带用户名、密码、仓库地址信息 docker login --username test --password test123 192.168.0.22:8000 docker login --username seong --password 3er4#ER$ 192.168.0.22:8…...

几道简单的题目练一下手感
第 1 题 【 问答题 】 • 找和为K的两个元素 在一个长度为n(n < 1000)的整数序列中,判断是否存在某两个元素之和为k。 时间限制:1000 内存限制:65536 输入 第一行输入序列的长度n和k,用空格分开。 第二行输入序列中的n个整数&a…...
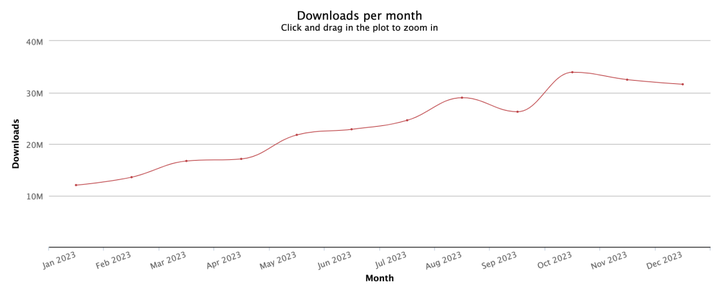
2023年哪个前端框架用的最多?
2023 年,TypeScript 的每月下载量持续稳定增长,年度累计下载量高达2,071,832,110(20.7 亿),展现了强大的市场需求和用户认可。 本文来通过详细的数据(2023 年 npm 累计下载量),看看…...
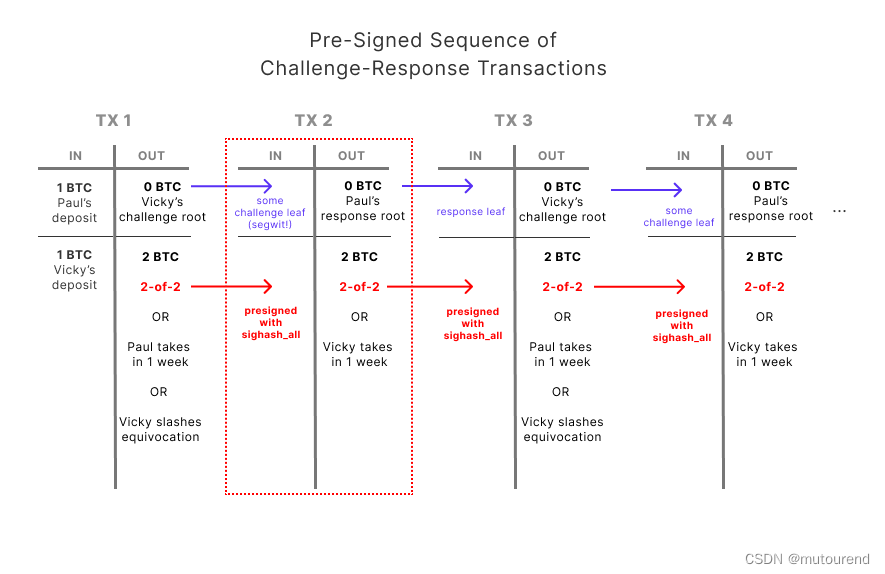
基于BitVM的乐观 BTC bridge
1. 引言 前序博客: 区块链互操作协议Bitcoin Bridge:治愈还是诅咒?BitVM:Bitcoin的链下合约 基于BitVM的乐观 BTC bridge: Trust-minimized two-way peg 机制 BitVM BTC bridge背后的主要思想是: 为比…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...
