机器学习中的10种非线性降维技术对比总结
降维意味着我们在不丢失太多信息的情况下减少数据集中的特征数量,降维算法属于无监督学习的范畴,用未标记的数据训练算法。
尽管降维方法种类繁多,但它们都可以归为两大类:线性和非线性。
线性方法将数据从高维空间线性投影到低维空间(因此称为线性投影)。例子包括PCA和LDA。
非线性方法提供了一种执行非线性降维(NLDR)的方法。我们经常使用NLDR来发现原始数据的非线性结构。当原始数据不可线性分离时,NLDR很有用。在某些情况下,非线性降维也被称为流形学习。
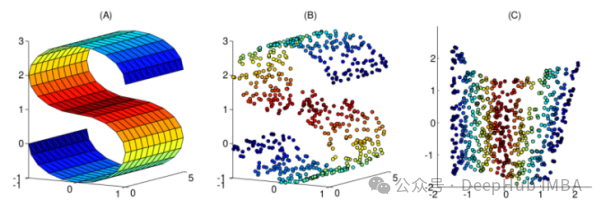
本文整理了10个常用的非线性降维技术,可以帮助你在日常工作中进行选择
1、核PCA
你们可能熟悉正常的PCA,这是一种线性降维技术。核PCA可以看作是正态主成分分析的非线性版本。
常规主成分分析和核主成分分析都可以进行降维。但是核PCA能很好地处理线性不可分割的数据。因此,核PCA算法的主要用途是使线性不可分的数据线性可分,同时降低数据的维数!
我们先创建一个非常经典的数据:
import matplotlib.pyplot as pltplt.figure(figsize=[7, 5])from sklearn.datasets import make_moonsX, y = make_moons(n_samples=100, noise=None, random_state=0)plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='plasma')plt.title('Linearly inseparable data')
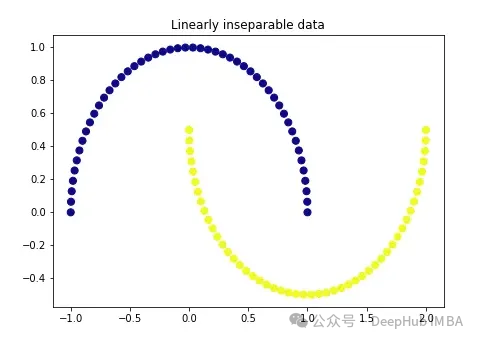
这两种颜色代表线性上不可分割的两类。我们不可能在这里画一条直线把这两类分开。
我们先使用常规PCA。
import numpy as npfrom sklearn.decomposition import PCApca = PCA(n_components=1)X_pca = pca.fit_transform(X)plt.figure(figsize=[7, 5])plt.scatter(X_pca[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')plt.title('First component after linear PCA')plt.xlabel('PC1')
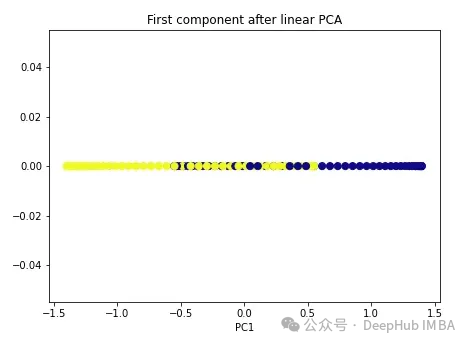
可以看到,这两个类仍然是线性不可分割的,现在我们试试核PCA。
import numpy as npfrom sklearn.decomposition import KernelPCAkpca = KernelPCA(n_components=1, kernel='rbf', gamma=15)X_kpca = kpca.fit_transform(X)plt.figure(figsize=[7, 5])plt.scatter(X_kpca[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')plt.axvline(x=0.0, linestyle='dashed', color='black', linewidth=1.2)plt.title('First component after kernel PCA')plt.xlabel('PC1')
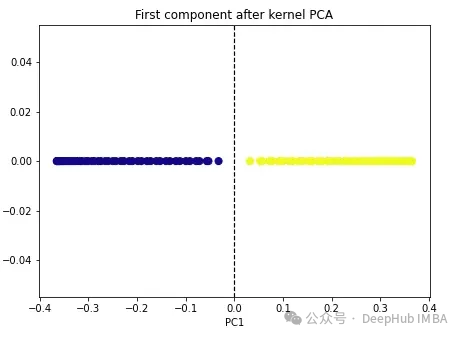
这两个类变成了线性可分的,核PCA算法使用不同的核将数据从一种形式转换为另一种形式。核PCA是一个两步的过程。首先核函数暂时将原始数据投影到高维空间中,在高维空间中,类是线性可分的。然后算法将该数据投影回n_components超参数(我们想要保留的维数)中指定的较低维度。
sklearn中有四个核选项:linear’, ‘poly’, ‘rbf’ and ‘sigmoid’。如果我们将核指定为“线性”,则将执行正常的PCA。任何其他核将执行非线性PCA。rbf(径向基函数)核是最常用的。
2、多维尺度变换(multidimensional scaling, MDS)
多维尺度变换是另一种非线性降维技术,它通过保持高维和低维数据点之间的距离来执行降维。例如,原始维度中距离较近的点在低维形式中也显得更近。
要在Scikit-learn我们可以使用MDS()类。
from sklearn.manifold import MDSmds = MDS(n_components, metric)mds_transformed = mds.fit_transform(X)
metric 超参数区分了两种类型的MDS算法:metric和non-metric。如果metric=True,则执行metric MDS。否则,执行non-metric MDS。
我们将两种类型的MDS算法应用于以下非线性数据。
import numpy as npfrom sklearn.manifold import MDSmds = MDS(n_components=1, metric=True) # Metric MDSX_mds = mds.fit_transform(X)plt.figure(figsize=[7, 5])plt.scatter(X_mds[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')plt.title('Metric MDS')plt.xlabel('Component 1')
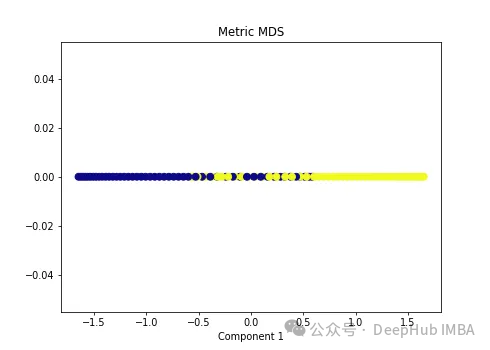
import numpy as npfrom sklearn.manifold import MDSmds = MDS(n_components=1, metric=False) # Non-metric MDSX_mds = mds.fit_transform(X)plt.figure(figsize=[7, 5])plt.scatter(X_mds[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')plt.title('Non-metric MDS')plt.xlabel('Component 1')
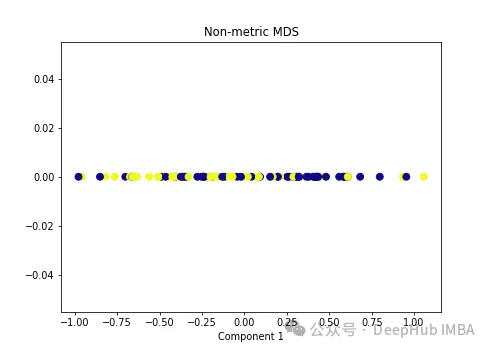
可以看到MDS后都不能使数据线性可分,所以可以说MDS不适合我们这个经典的数据集。
3、Isomap
Isomap(Isometric Mapping)在保持数据点之间的地理距离,即在原始高维空间中的测地线距离或者近似的测地线距离,在低维空间中也被保持。Isomap的基本思想是通过在高维空间中计算数据点之间的测地线距离(通过最短路径算法,比如Dijkstra算法),然后在低维空间中保持这些距离来进行降维。在这个过程中,Isomap利用了流形假设,即假设高维数据分布在一个低维流形上。因此,Isomap通常在处理非线性数据集时表现良好,尤其是当数据集包含曲线和流形结构时。
import matplotlib.pyplot as pltplt.figure(figsize=[7, 5])from sklearn.datasets import make_moonsX, y = make_moons(n_samples=100, noise=None, random_state=0)import numpy as npfrom sklearn.manifold import Isomapisomap = Isomap(n_neighbors=5, n_components=1)X_isomap = isomap.fit_transform(X)plt.figure(figsize=[7, 5])plt.scatter(X_isomap[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')plt.title('First component after applying Isomap')plt.xlabel('Component 1')
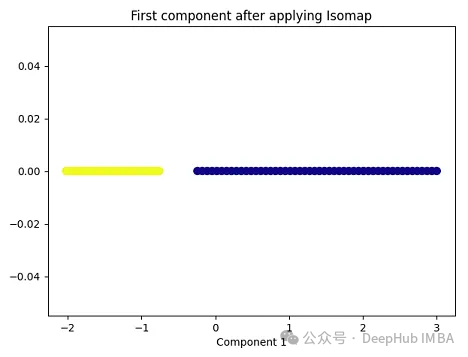
就像核PCA一样,这两个类在应用Isomap后是线性可分的!
4、Locally Linear Embedding(LLE)
与Isomap类似,LLE也是基于流形假设,即假设高维数据分布在一个低维流形上。LLE的主要思想是在局部邻域内保持数据点之间的线性关系,并在低维空间中重构这些关系。
from sklearn.manifold import LocallyLinearEmbeddinglle = LocallyLinearEmbedding(n_neighbors=5,n_components=1)lle_transformed = lle.fit_transform(X)plt.figure(figsize=[7, 5])plt.scatter(lle_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')plt.title('First component after applying LocallyLinearEmbedding')plt.xlabel('Component 1')
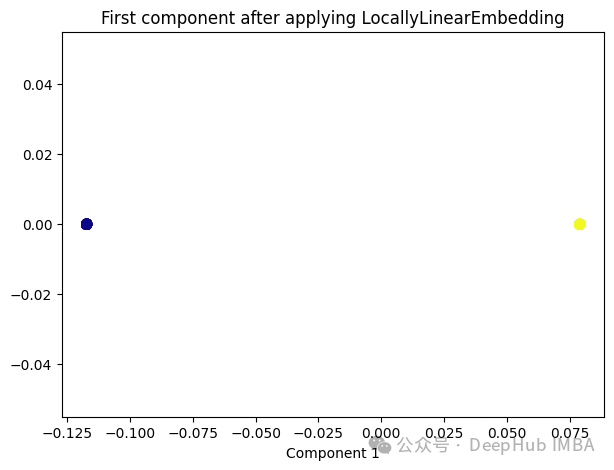
只有2个点,其实并不是这样,我们打印下这个数据
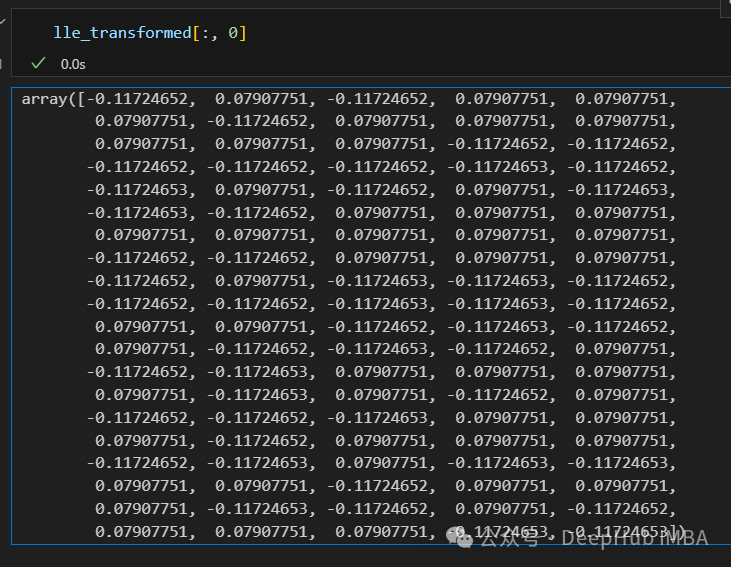
可以看到数据通过降维变成了同一个数字,所以LLE降维后是线性可分的,但是却丢失了数据的信息。
5、Spectral Embedding
Spectral Embedding是一种基于图论和谱理论的降维技术,通常用于将高维数据映射到低维空间。它的核心思想是利用数据的相似性结构,将数据点表示为图的节点,并通过图的谱分解来获取低维表示。
from sklearn.manifold import SpectralEmbeddingsp_emb = SpectralEmbedding(n_components=1, affinity='nearest_neighbors')sp_emb_transformed = sp_emb.fit_transform(X)plt.figure(figsize=[7, 5])plt.scatter(sp_emb_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')plt.title('First component after applying SpectralEmbedding')plt.xlabel('Component 1')
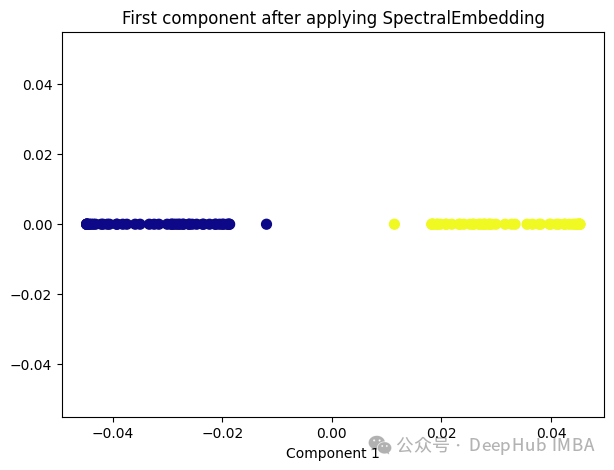
6、t-Distributed Stochastic Neighbor Embedding (t-SNE)
t-SNE的主要目标是保持数据点之间的局部相似性关系,并在低维空间中保持这些关系,同时试图保持全局结构。
from sklearn.manifold import TSNEtsne = TSNE(1, learning_rate='auto', init='pca')tsne_transformed = tsne.fit_transform(X)plt.figure(figsize=[7, 5])plt.scatter(tsne_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')plt.title('First component after applying TSNE')plt.xlabel('Component 1')
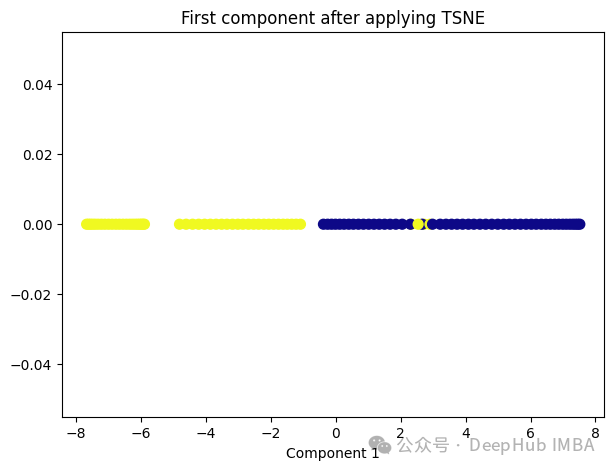
t-SNE好像也不太适合我们的数据。
7、Random Trees Embedding
Random Trees Embedding是一种基于树的降维技术,常用于将高维数据映射到低维空间。它利用了随机森林(Random Forest)的思想,通过构建多棵随机决策树来实现降维。
Random Trees Embedding的基本工作流程:
- 构建随机决策树集合:首先,构建多棵随机决策树。每棵树都是通过从原始数据中随机选择子集进行训练的,这样可以减少过拟合,提高泛化能力。
- 提取特征表示:对于每个数据点,通过将其在每棵树上的叶子节点的索引作为特征,构建一个特征向量。每个叶子节点都代表了数据点在树的某个分支上的位置。
- 降维:通过随机森林中所有树生成的特征向量,将数据点映射到低维空间中。通常使用降维技术,如主成分分析(PCA)或t-SNE等,来实现最终的降维过程。
Random Trees Embedding的优势在于它的计算效率高,特别是对于大规模数据集。由于使用了随机森林的思想,它能够很好地处理高维数据,并且不需要太多的调参过程。
RandomTreesEmbedding使用高维稀疏进行无监督转换,也就是说,我们最终得到的数据并不是一个连续的数值,而是稀疏的表示。所以这里就不进行代码展示了,有兴趣的看看sklearn的sklearn.ensemble.RandomTreesEmbedding
8、Dictionary Learning
Dictionary Learning是一种用于降维和特征提取的技术,它主要用于处理高维数据。它的目标是学习一个字典,该字典由一组原子(或基向量)组成,这些原子是数据的线性组合。通过学习这样的字典,可以将高维数据表示为一个更紧凑的低维空间中的稀疏线性组合。
Dictionary Learning的优点之一是它能够学习出具有可解释性的原子,这些原子可以提供关于数据结构和特征的重要见解。此外,Dictionary Learning还可以产生稀疏表示,从而提供更紧凑的数据表示,有助于降低存储成本和计算复杂度。
from sklearn.decomposition import DictionaryLearningdict_lr = DictionaryLearning(n_components=1)dict_lr_transformed = dict_lr.fit_transform(X)plt.figure(figsize=[7, 5])plt.scatter(dict_lr_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')plt.title('First component after applying DictionaryLearning')plt.xlabel('Component 1')
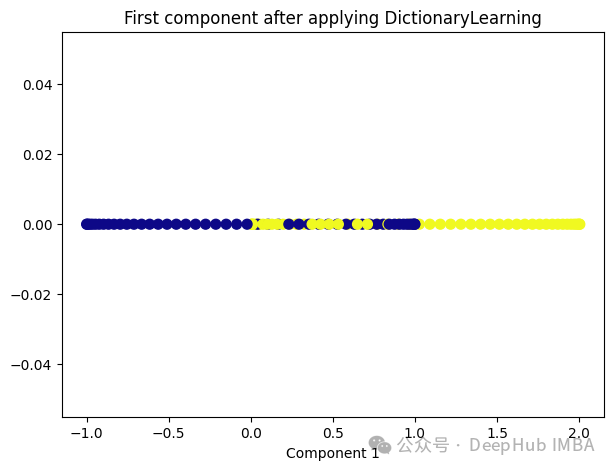
9、Independent Component Analysis (ICA)
Independent Component Analysis (ICA) 是一种用于盲源分离的统计方法,通常用于从混合信号中估计原始信号。在机器学习和信号处理领域,ICA经常用于解决以下问题:
- 盲源分离:给定一组混合信号,其中每个信号是一组原始信号的线性组合,ICA的目标是从混合信号中分离出原始信号,而不需要事先知道混合过程的具体细节。
- 特征提取:ICA可以被用来发现数据中的独立成分,提取数据的潜在结构和特征,通常在降维或预处理过程中使用。
ICA的基本假设是,混合信号中的各个成分是相互独立的,即它们的统计特性是独立的。这与主成分分析(PCA)不同,PCA假设成分之间是正交的,而不是独立的。因此ICA通常比PCA更适用于发现非高斯分布的独立成分。
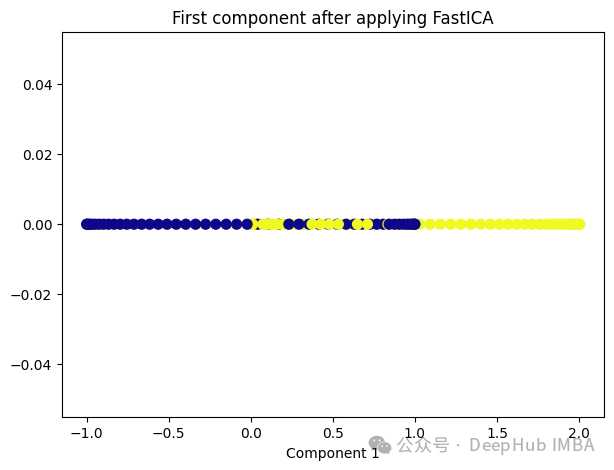
from sklearn.decomposition import FastICAica = FastICA(n_components=1, whiten='unit-variance')ica_transformed = dict_lr.fit_transform(X)plt.figure(figsize=[7, 5])plt.scatter(ica_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma')plt.title('First component after applying FastICA')plt.xlabel('Component 1')
10、Autoencoders (AEs)
到目前为止,我们讨论的NLDR技术属于通用机器学习算法的范畴。而自编码器是一种基于神经网络的NLDR技术,可以很好地处理大型非线性数据。当数据集较小时,自动编码器的效果可能不是很好。
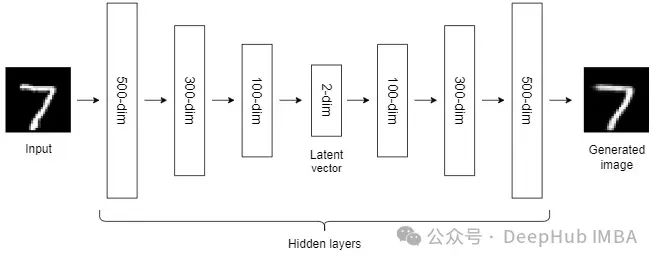
自编码器我们已经介绍过很多次了,所以这里就不详细说明了。
总结
非线性降维技术是一类用于将高维数据映射到低维空间的方法,它们通常适用于数据具有非线性结构的情况。
大多数NLDR方法基于最近邻方法,该方法要求数据中所有特征的尺度相同,所以如果特征的尺度不同,还需要进行缩放。
另外这些非线性降维技术在不同的数据集和任务中可能表现出不同的性能,因此在选择合适的方法时需要考虑数据的特征、降维的目标以及计算资源等因素。
https://avoid.overfit.cn/post/0d7e9cf08e72486faf46fe341e96e468
相关文章:

机器学习中的10种非线性降维技术对比总结
降维意味着我们在不丢失太多信息的情况下减少数据集中的特征数量,降维算法属于无监督学习的范畴,用未标记的数据训练算法。 尽管降维方法种类繁多,但它们都可以归为两大类:线性和非线性。 线性方法将数据从高维空间线性投影到低维空间(因此…...

[ubuntu]split命令分割文件
split 命令 $ split --help Usage: split [OPTION]... [INPUT [PREFIX]] Output fixed-size pieces of INPUT to PREFIXaa, PREFIXab, ...; default size is 1000 lines, and default PREFIX is x. With no INPUT, or when INPUT is -, read standard input.Mandatory argume…...

《小强升职记:时间管理故事书》阅读笔记
目录 前言 一、你的时间都去哪儿了 1.1 你真的很忙吗 1.2 如何记录和分析时间日志 1.3 如何找到自己的价值观 二、无压工作法 2.1 传说中的“四象限法则 2.2 衣柜整理法 三、行动时遇到问题怎么办? 3.1 臣服与拖延 3.2 如何做到要事第一? 3.…...
visual studio code could not establish connection to *: XHR failed
vscode远程连接服务器时,输入密码,又重新提示输入密码,就这样循环了好几次,然后会报上述的错误。由于我是window系统,我用cmd,然后ssh */你的IP地址/*发现可以远程到服务器上,但是通过Vscode就不…...

JVM-面试题
一、对象 1、对象创建 类加载检查 虚拟机遇到一条new指令时,首先将去检查这个指令的参数是否能在常量池定位到类的符号引用,并且检查这个符号引用代表的类是否被加载、解析和初始化过。若没有,必须先执行类加载过程。分配内存 类加载检查通过后,jvm将为新生对象分配内存,…...

计算机网络——多媒体网络
前些天发现了一个巨牛的人工智能学习网站 通俗易懂,风趣幽默,忍不住分享一下给大家, 跳转到网站 小程一言 我的计算机网络专栏,是自己在计算机网络学习过程中的学习笔记与心得,在参考相关教材,网络搜素…...
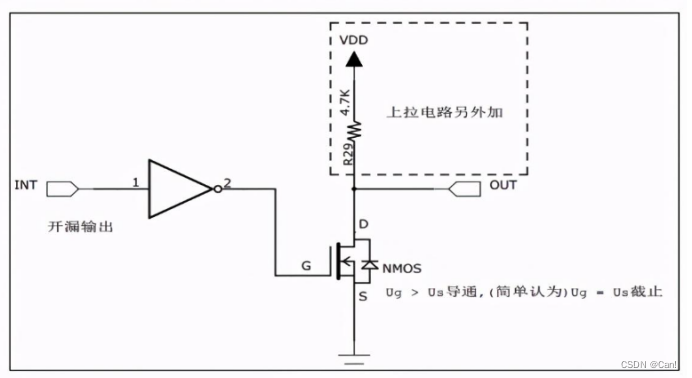
GPIO八种工作模式
目录 一、推挽输出 二、开漏输出 三、复用推挽输出 四、复用开漏输出 五、浮空输入 六、上拉输入 七、下拉输入 八、模拟输入 GPIO八种配置模式,原理和使用场景,硬件原理如下图: 一、推挽输出 1、 原理 当控制栅极为低电平时&#x…...
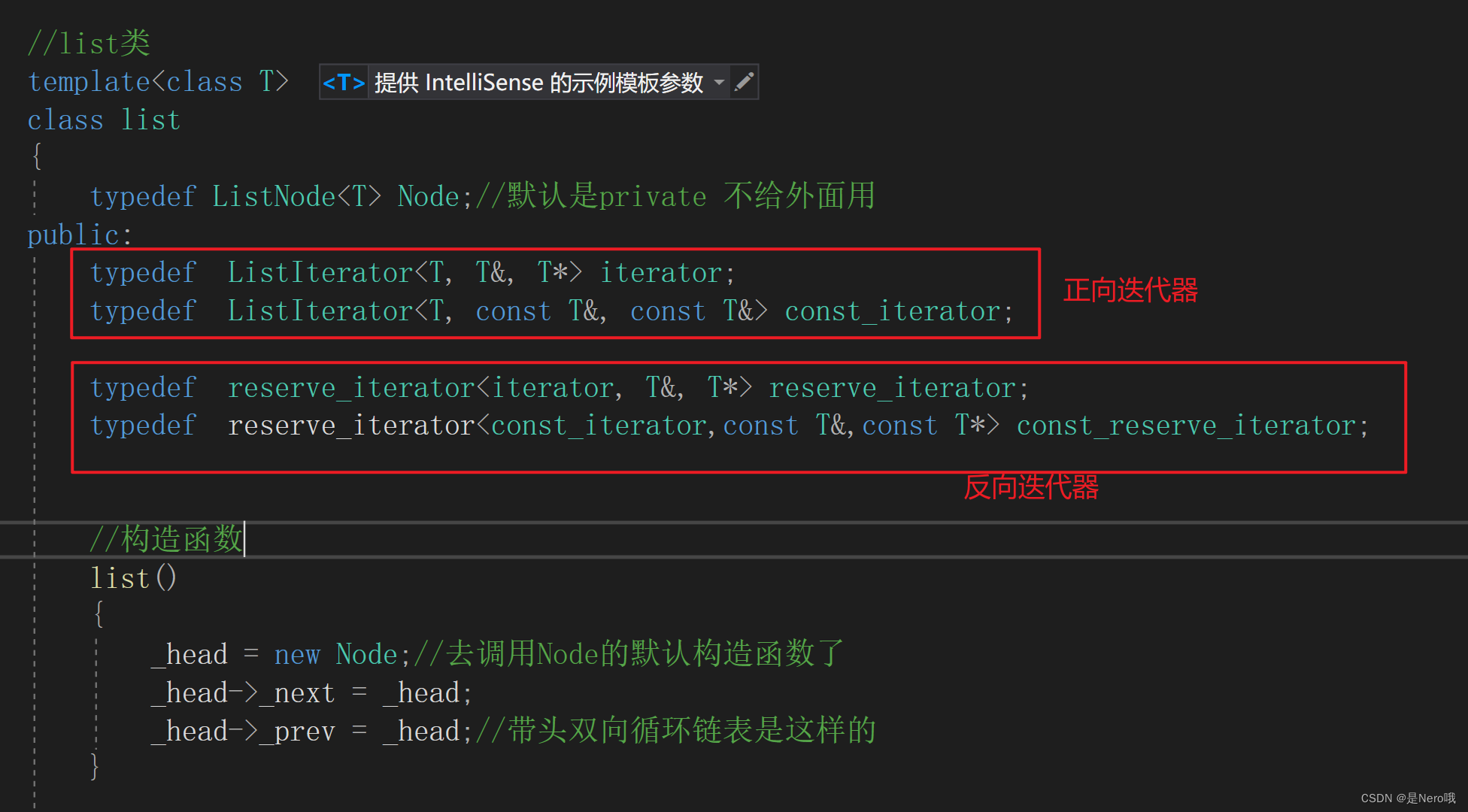
C++初阶:适合新手的手撕list(模拟实现list)
上次讲了常用的接口:今天就来进行模拟实现啦 文章目录 1.基本结构与文件规划2.空参构造函数(constructor)3.完善迭代器(iterator)(begin(),end())4.List Capacity(size(),empty())4.增删改查(push_back,pop_back,pop_f…...
js手写Promise(上)
目录 构造函数resolve与reject状态改变状态改变后就无法再次改变 代码优化回调函数中抛出错误 thenonFulfilled和onRejected的调用时机异步then多个then 如果是不知道或者对Promise不熟悉的铁铁可以先看我这篇文章 Promise 构造函数 在最开始,我们先不去考虑Promi…...

基于Web技术的家居室内温湿度监测系统
设计一个基于Web技术的家居室内温湿度监测系统涉及前端和后端开发,以及与硬件传感器的集成。以下是一个简单的设计概述: ### 1. 系统架构 - **前端**: 用户界面,用于显示实时数据和历史记录,可通过Web浏览器访问。 - **后端**: 服…...

ubuntu22.04@laptop OpenCV Get Started: 009_image_thresholding
ubuntu22.04laptop OpenCV Get Started: 009_image_thresholding 1. 源由2. image_thresholding应用Demo2.1 C应用Demo2.2 Python应用Demo 3. 重点分析3.1 Binary Thresholding ( THRESH_BINARY )3.2 Inverse-Binary Thresholding ( THRESH_BINARY_INV )3.3 Truncate Threshold…...

Zeek实战—快速构建流量安全能力
第1章 网络流量与网络安全 1.2流量与网络 从宏观角度进行观察,如果将计算机网络看作一个整体,可以很容易抽象出它是由以下3个部分组成的。 1.网络终端。指连接在网络中的、能够产生或消费网络流量的软/硬件系统,是网络流量在正常情况下的…...

vim命令编辑完文件后,按ESC键退出编辑模式,无法进入命令模式解决方案
发现问题 在Vim编辑器中,我们通常需要按Esc键来退出编辑模式并进入命令模式。但有时,你可能会发现即使按了Esc键,也无法进入命令模式。这可能是由于某些设置或插件导致的。不过,有一个解决办法可以帮助你解决这个问题。 解决办法…...

【生产实测有效】Linux磁盘清理常用命令
经常遇到磁盘空间告警需要清理 常用方法 磁盘空间分析 先查看整体磁盘空间使用情况 df -Th lsblk 再有针对性的查看使用率过高的磁盘 du -hsx --exclude/{proc,sys,dev,boot,home,tmp,usr,var,app,ncltybbpo} /*查找大文件 find . -type d -exec tar -cjvf {}.tar.bz2 {…...

练习:鼠标类设计之1_类内容解析
前言 光做理论上的总结,不做练习理解不会那么深刻 做类的练习,解析类里面的内容有哪些 引入 电脑使用最频繁的两个外设:鼠标和键盘,他们每时每刻都在和用户交互,试做一个鼠标类 思路 我们现在要做一个鼠标类,这个类是属于能动类还是资源类呢?鼠标似乎自己做不了什么,需要和其…...
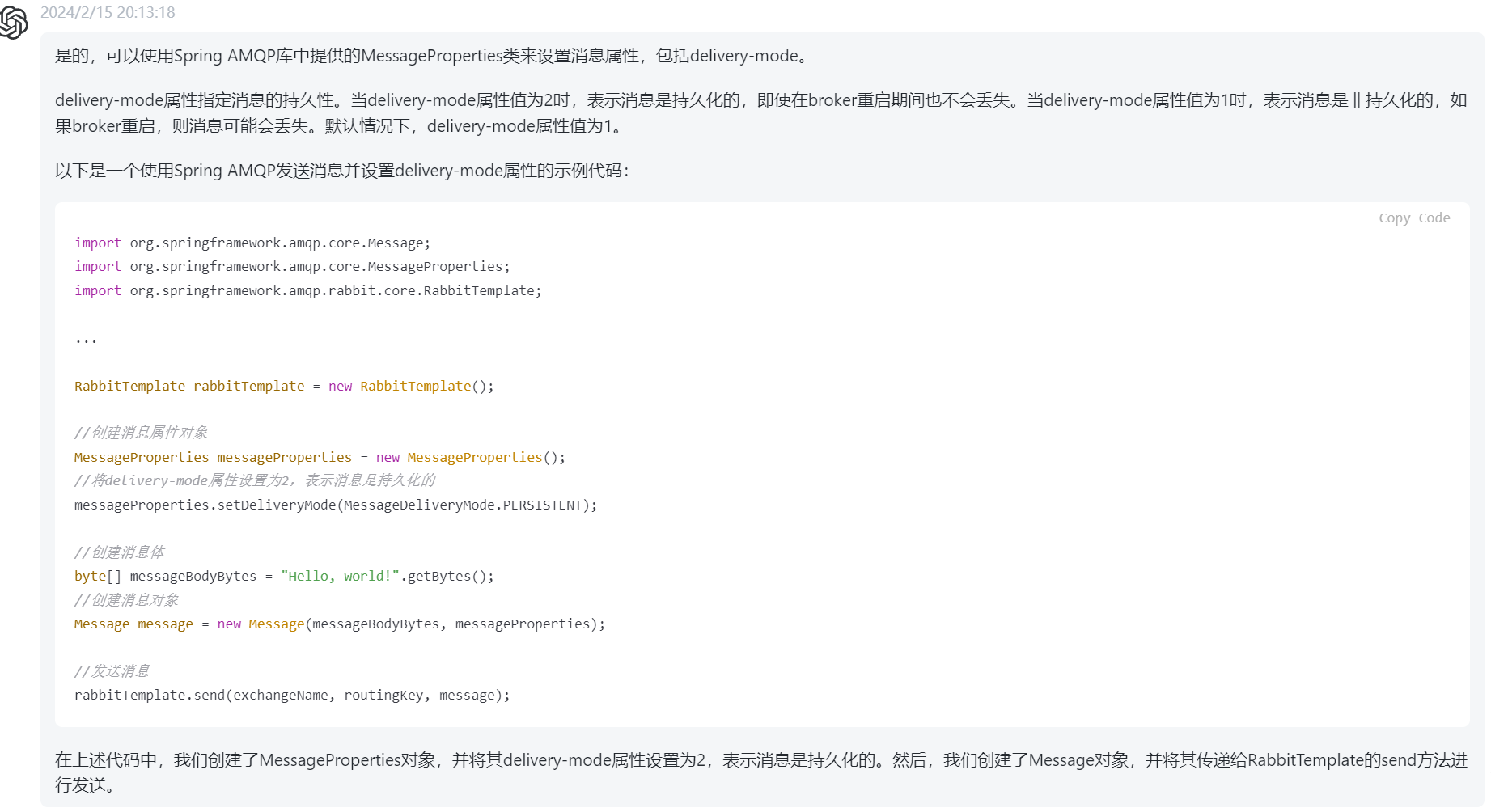
消息队列RabbitMQ-使用过程中面临的问题与解决思路
消息队列在使用过程中会出现很多问题 首先就是消息的可靠性,也就是消息从发送到消费者接收,消息在这中间过程中可能会丢失 生产者到交换机的过程、交换机到队列的过程、消息队列中、消费者接收消息的过程中,这些过程中消息都可能会丢失。 …...
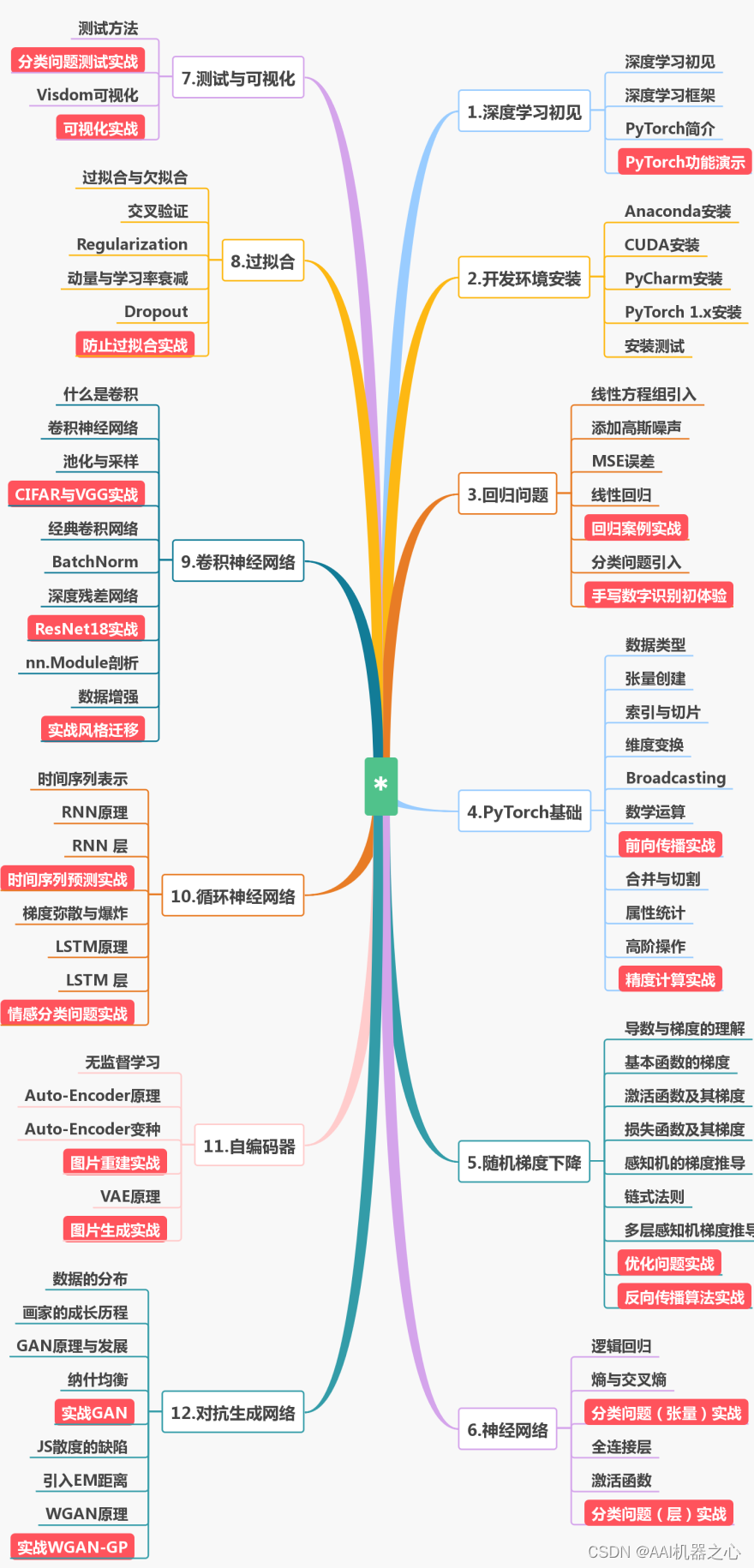
搜索Agent方案
为啥需要整体方案,直接调用搜索接口取Top1返回不成嘛?要是果真如此Simple&Naive,New Bing岂不是很容易复刻->.-> 我们先来看个例子,前一阵火爆全网的常温超导技术,如果想回答LK99哪些板块会涨,你…...

排序算法---计数排序
原创不易,转载请注明出处。欢迎点赞收藏~ 计数排序(Counting Sort)是一种线性时间复杂度的排序算法,其核心思想是通过统计待排序元素的个数来确定元素的相对位置,从而实现排序。 具体的计数排序算法步骤如下ÿ…...

STM32——LCD(1)认识
目录 一、初识LCD 1. LCD介绍 2. 显示器的分类 3. 像素 4. LED和OLED显示器 5. 显示器的基本参数 (1)像素 (2)分辨率 (3)色彩深度 (4)显示器尺寸 (5ÿ…...
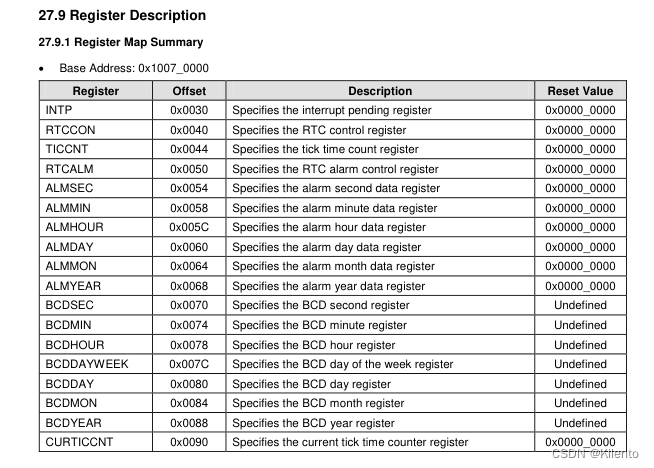
iTop-4412 裸机程序(二十二)- RTC时钟
目录 0.源码1. RTC2. iTop4412 中的 RTC使用的相关寄存器3. BCD编码4. 关键源码 0.源码 GitHub:https://github.com/Kilento/4412NoOS 1. RTC RTC是实时时钟(Real Time Clock)的缩写,是一种用于计算机系统的硬件设备࿰…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
