C++学习:二分查找
二分查找的前提
库函数只能对数组进行二分查找。
对一个数组进行二分查找的前提是这个数组中的元素是单调的。
一般为单调不减,当然如果是单调不增也可以(需要修改比较函数)
例如:
[1,5,5,9,18]是单调的
[1 , 9, 9, 7, 15]不是单调的
[9,8,8,7,7,1]是单调的
binary_search函数
binary_search是C++标准库中的一个算法函数,用于在已排序的序列(例如数组或容器vector)中查找特定元素。
它通过二分查找算法来确定序列中是否存在目标元素。
函数返回一个bool值,表示目标元素是否存在于序列中。
如果需要获取找到的元素的位置,可以使用std::lower_bound函数或std::upper_bound函数。
vector <int> numbers = {1, 3, 5 , 7 ,9};int target = 5;bool found = binary_search(number.begin(),number.end(),target);if(found){cout << "Target element" << target << "found." << endl;
}else{cout << "Target element" << target << "not found." << endl;
}
lower_bound和upper_bound
前提:数组必须为非降序
如果要在非升序的数组中使用,可以通过修改比较函数实现(方法与sort自定义比较函数类似)
lower_bound(st,ed,_x)返回地址[st, ed)中第一个大于等于x的元素的地址
upper_bound(st,ed,x)返回地址[st,ed)中第一个大于x的元素的地址
如果不存在则返回最后一个元素的下一个位置,在vector中即end()
地址-首地址=下标
[lower_bound , upper_bound)
//初始化
vector <int> v={5,1,7,3,10,18,9};
//排序
sort(v.begin(),v.end());
for(auto &i : v)cout<< i<<'cout<<'\n';
//找到数组中第一个大于等于8的元素的位置
cout<<(lower_bound(v.begin(),v.end(),8)- v.begin())<<'\n';
例题:
#include <bits/stdc++.h>
using namespace std;
int main(void)
{int data[200];for(int i = 0 ; i < 200 ; i ++)data[i] = 4 * i + 6;int target = 0;cin >> target;cout << (lower_bound(data,data+200,target)- data);return 0;
}
相关文章:

C++学习:二分查找
二分查找的前提 库函数只能对数组进行二分查找。 对一个数组进行二分查找的前提是这个数组中的元素是单调的。 一般为单调不减,当然如果是单调不增也可以(需要修改比较函数) 例如: [1,5,5,9,18]是单调的 [1 , 9, 9,…...

语言与科技创新(大语言模型对科技创新的影响)
1.语言因素对科技创新的影响 科技创新中的语言因素至关重要,具体体现在以下几个方面: 科技文献交流: 英语作为全球科学研究的通用语言,极大地推动了科技成果的国际传播与合作。在国际上,科学家们在发表论文、报告研究…...

【C语言】简单贪吃蛇实现保姆级教学!!!
关注小庄 顿顿解馋૮(˶ᵔ ᵕ ᵔ˶)ა 新年快乐呀小伙伴 引言: 小伙伴们应该都有一个做游戏的梦吧?今天让小庄来用C语言简单实现一下我们的童年邪典贪吃蛇,顺便巩固我们的C语言知识,请安心食用~ 文章目录 贪吃蛇效果一.游戏前工作…...

rtt设备io框架面向对象学习-uart设备
目录 1.uart设备基类2.uart设备基类的子类3.初始化/构造流程3.1设备驱动层3.2 设备驱动框架层3.3 设备io管理层 4.总结5.使用 1.uart设备基类 此层处于设备驱动框架层。也是抽象类。 在/ components / drivers / include / drivers 下的serial.h定义了如下uart设备基类 struc…...
)
Innodb下修改事务工作流程(buffer pool、redo log、undolog)
1、在Buffer Pool中读取数据:当InnoDB需要更新一条记录时,首先会在Buffer Pool中查找该记录是否在内存中。如果没有在内存中,则从磁盘读取该页到Buffer Pool中。 2、记录UndoLog:在修改操作前,InnoDB会在Undo Log中记…...

redis为什么使用跳跃表而不是树
Redis中支持五种数据类型中有序集合Sorted Set的底层数据结构使用的跳跃表,为何不使用其他的如平衡二叉树、b树等数据结构呢? 1,redis的设计目标、性能需求: redis是高性能的非关系型(NoSQL)内存键值数据…...

【matalab】基于Octave的信号处理与滤波分析案例
一、基于Octave的信号处理与滤波分析案例 GNU Octave是一款开源软件,类似于MATLAB,广泛用于数值计算和信号处理。 一个简单的信号处理与滤波分析案例,说明如何在Octave中生成一个有噪声的信号,并设计一个滤波器来去除噪声。 首…...

Elasticsearch:特定领域的生成式 AI - 预训练、微调和 RAG
作者:来自 Elastic Steve Dodson 有多种策略可以将特定领域的知识添加到大型语言模型 (LLM) 中,并且作为积极研究领域的一部分,正在研究更多方法。 对特定领域数据集进行预训练和微调等方法使 LLMs 能够推理并生成特定领域语言。 然而&#…...

HarmonyOS—UI 开发性能提升的推荐方法
开发者若使用低性能的代码实现功能场景可能不会影响应用的正常运行,但却会对应用的性能造成负面影响。本章节列举出了一些可提升性能的场景供开发者参考,以避免应用实现上带来的性能劣化。 使用数据懒加载 开发者在使用长列表时,如果直接采用…...

84 CTF夺旗-PHP弱类型异或取反序列化RCE
目录 案例1:PHP-相关总结知识点-后期复现案例2:PHP-弱类型对比绕过测试-常考点案例3:PHP-正则preg_match绕过-常考点案例4:PHP-命令执行RCE变异绕过-常考点案例5:PHP-反序列化考题分析构造复现-常考点涉及资源…...
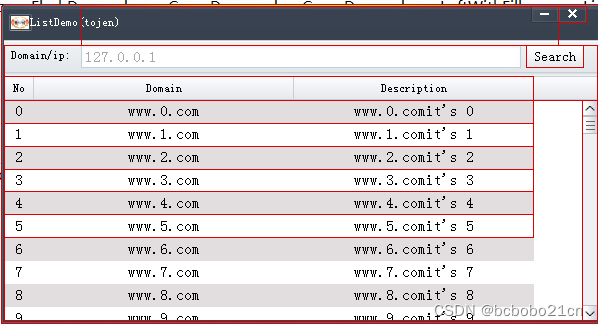
Duilib List 控件学习
这是自带的一个示例; 一开始运行的时候List中是空的,点击Search按钮以后就填充列表框; 先看一下列表框列头是在xml文件中形成的; <List name="domainlist" bkcolor="#FFFFFFFF" ... menu="true"> <ListHeader height="24…...

详细了解Node.js的配置与使用!
详细了解Node.js的配置与使用! Node.js 是一个基于 Chrome V8 引擎的 JavaScript 运行环境。它允许开发者在服务器端运行 JavaScript,从而实现全栈 JavaScript 开发。本文将介绍 Node.js 的配置和 npm 的应用。 一、Node.js 配置 下载与安装 首先&…...

OpenCV 移动最小二乘图像变形
文章目录 一、简介二、实现代码三、实现效果参考文献一、简介 在现实生活中,我们常常应用一些刚性的变换来实现物体的旋转平移,对于非刚性的变换我们都没有在意,其实这种变换也是无处不在的,如我们经常看的动画就可以通过一些非刚性的变换达到一些非常夸张的效果。这里,我…...

【深度学习】S2 数学基础 P4 概率论
目录 基本概率论概率论公理随机变量 多个随机变量联合概率条件概率贝叶斯定理求和法则独立性 期望与方差小结 基本概率论 机器学习本质上,就是做出预测。而概率论提供了一种量化和表达不确定性水平的方法,可以帮助我们量化对某个结果的确定性程度。 在…...

跟我学c++中级篇——静态多态
一、多态 Polymorphism,多态。学习过c的人如果不知道多态,基本上就是打入c内部的C程序员了。在前边曾经对多态进行过分析,对其中的虚函数(虚表等)也进行过较为详细的说明。 多态其实非常好理解,不要硬扣书…...
)
设计模式--桥接模式(Bridge Pattern)
桥接模式(Bridge Pattern)是一种结构型设计模式,它主要是用于将抽象部分与实现部分分离,使它们可以独立地变化。 桥接模式主要包含以下几个角色: Abstraction(抽象类):定义抽象类的…...
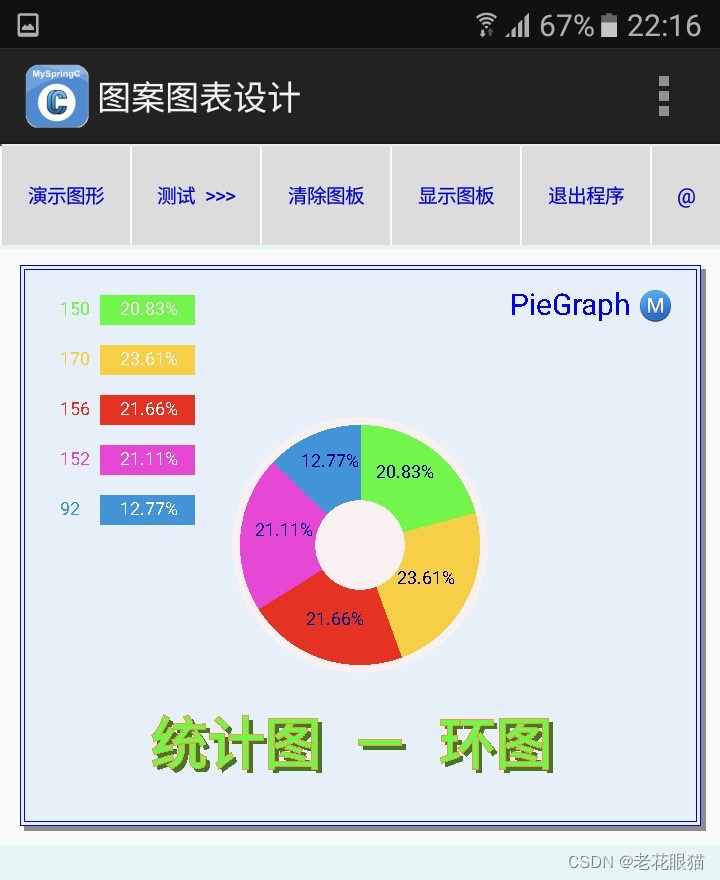
统计图饼图绘制方法(C语言)
统计图饼图绘制方法(C语言) 常用的统计图有条形图、柱形图、折线图、曲线图、饼图、环形图、扇形图。 前几类图比较容易绘制,饼图绘制较难。今值此介绍饼图的绘制方法。 本方法采用C语言的最基本功能: ( 1.)…...

洛谷C++简单题小练习day12—寻找最小值小程序
day12--寻找最小值--2.16 习题概述 题目描述 给出 n 和 n 个整数 ai,求这 n 个整数中最小值是什么。 输入格式 第一行输入一个正整数 n,表示数字个数。 第二行输入 n 个非负整数,表示 1,2…a1,a2…an,以空格隔开。 …...

相机图像质量研究(13)常见问题总结:光学结构对成像的影响--鬼影
系列文章目录 相机图像质量研究(1)Camera成像流程介绍 相机图像质量研究(2)ISP专用平台调优介绍 相机图像质量研究(3)图像质量测试介绍 相机图像质量研究(4)常见问题总结:光学结构对成像的影响--焦距 相机图像质量研究(5)常见问题总结:光学结构对成…...
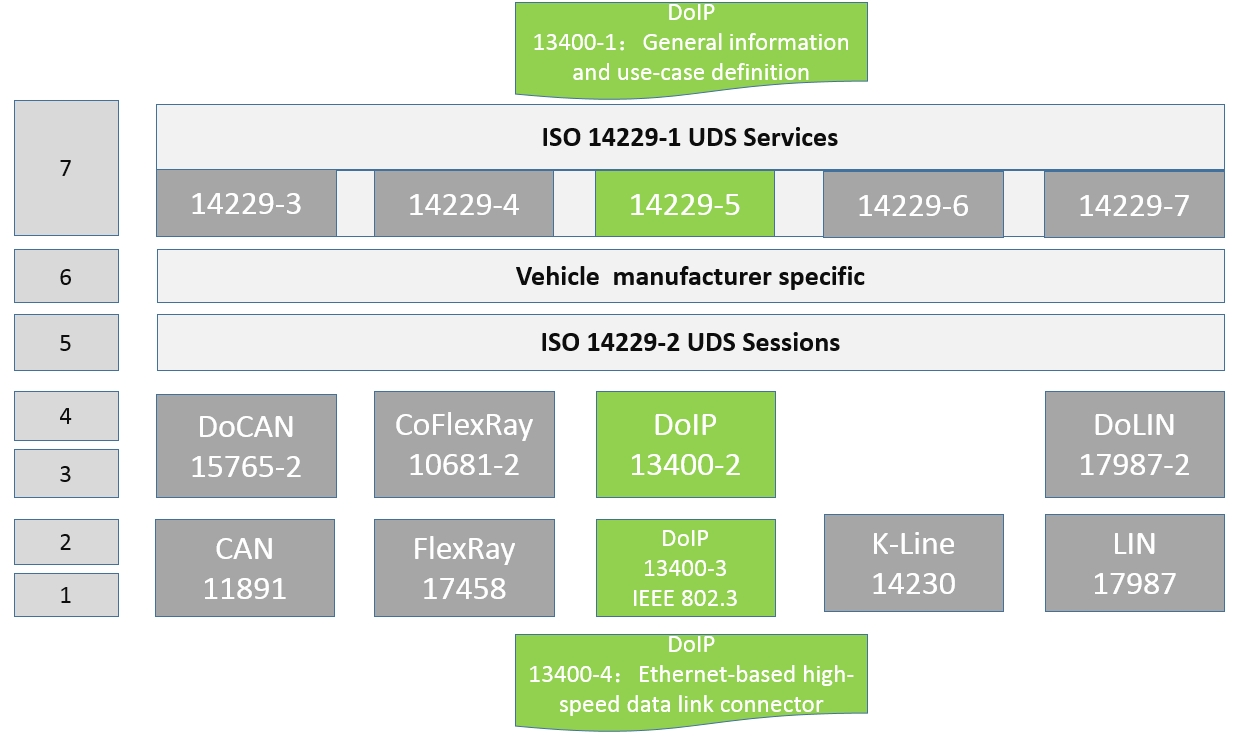
车载诊断协议DoIP系列 —— 车辆以太网节点需求汇总
车载诊断协议DoIP系列 —— 车辆以太网节点需求汇总 我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师(Wechat:gongkenan2013)。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 本就是小人物,输了就是输了,不要在意别人怎么看自己。江湖一碗茶,…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...
