MATLAB计算极限和微积分
一.函数与极限
计算极限:lim(3*x^2/(2x+1)),x分别趋于0和1,代码如下:
syms x;
limit(3*x*x/(2*x+1),x,0)
limit(3*x*x/(2*x+1),x,1)结果分别为0和1:

1.计算双侧极限
计算极限:lim(3*x^2/(2x+1)),x分别趋于0和1,代码如下:
syms x;
limit(3*x*x/(2*x+1),x,0)
limit(3*x*x/(2*x+1),x,1)2.计算单侧极限
分别计算当x从左右两边趋向0时,1/x的极限值:
syms x;
limit(1/x,x,0,'left')
limit(1/x,x,0,'right')结果分别为负无穷和正无穷:

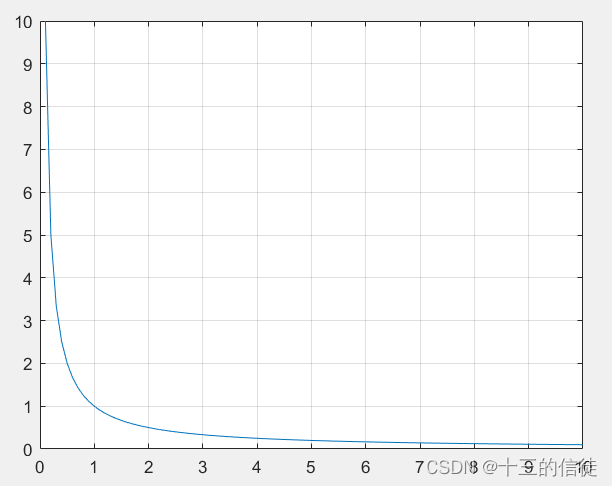
3.绘制极限图像
clear
clc
syms n
x=1/n;
y=inline(x);
max=10;
n=0:0.1:max;
figure
plot(n,y(n))
grid on
hold on如下:最大值max、间距均可以根据实际情况做出调整~
二.导数与微分
1.一阶导数
syms x
diff(sin(2*x))结果为:2cos2x

Tips:
在MATLAB中书写要严谨,sin2x要写成sin(2*x),千万不要习惯性简写~
2.高阶导数
计算:3(x^4)+4(x^2)+cos(2*x)的三阶导数:
一阶导如下:
三阶导如下:
-
syms x -
diff(3*(x^4)+4*(x^2)+cos(2*x),x,3)

3.参数方程求导
设参数方程:
- x=3*sin(2*n)
- y=arcsin(n^2)
syms n
x=3*sin(2*n)
y=asin(n^2)
diff(y)/diff(x)
%pretty(diff(y)/diff(x))
三.微分中值定理及其应用
四.不定积分
1.极值与最值
求极值,一个想法是求出一阶导为0的点,不过这样需要人为判断是极大值还是极小值,以及结合单调性判断必要条件~
syms x y
y=sin(x)+cos(2*x);
num=diff(y);
solve(num)
求最值,这里使用了内联函数,本质上还是暴力搜索,所以搜索范围和搜索间隔的选择很重要,其实甚至可以使用遗传算法和模拟退火,不过这里是考研数学,就不展开写高难度的算法了~
clear
clct= -100:0.0001:100; syms x;
y = inline(x^2+5*x+12); max = max(y(t));
min = min(y(t));(相比之下还是用极值法比较简易。。。)
2.单调区间
f = @(x) x.^2 + 2*x + 1; %函数句柄的写法
x = -10:0.1:10;
y = f(x);
dy = diff(y);%计算一阶微分
方法不够严谨,只能根据一阶微分大致估计一下单调性变化的点~
3.渐近线
(本质还是求极限,列出公式调用limit函数限即可,此处暂略~)
五.定积分
syms x y;%变量
f=sin(2*x)+3*cos(3*x)+3*x+3; %目标函数式
int(f,'x')%求解不定积分,两个参数分别为积分表达式和被积变量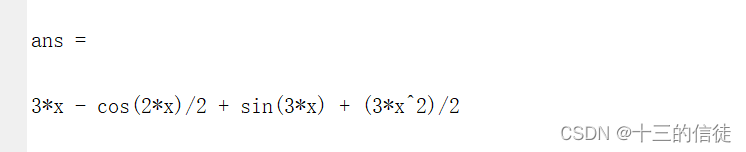 (注意不定积分往往答案不唯一,若答案不一致可以尝试变形看看与自己算的结果是否一致~)
(注意不定积分往往答案不唯一,若答案不一致可以尝试变形看看与自己算的结果是否一致~)
六.定积分的应用
(基本上是一些应用题~)
相关文章:
MATLAB计算极限和微积分
一.函数与极限 计算极限:lim(3*x^2/(2x1)),x分别趋于0和1,代码如下: syms x; limit(3*x*x/(2*x1),x,0) limit(3*x*x/(2*x1),x,1) 结果分别为0和1: 1.计算双侧极限 计算极限:lim(3*x^2/(2x1))࿰…...

在数组中插入元素
问题:假设有一个数组{1,2,3,4,5},如果我们要在3之后插入一个数(520),这该怎么办呢? 思路:要想在以元素3之后插入一个元素,我们先要做…...
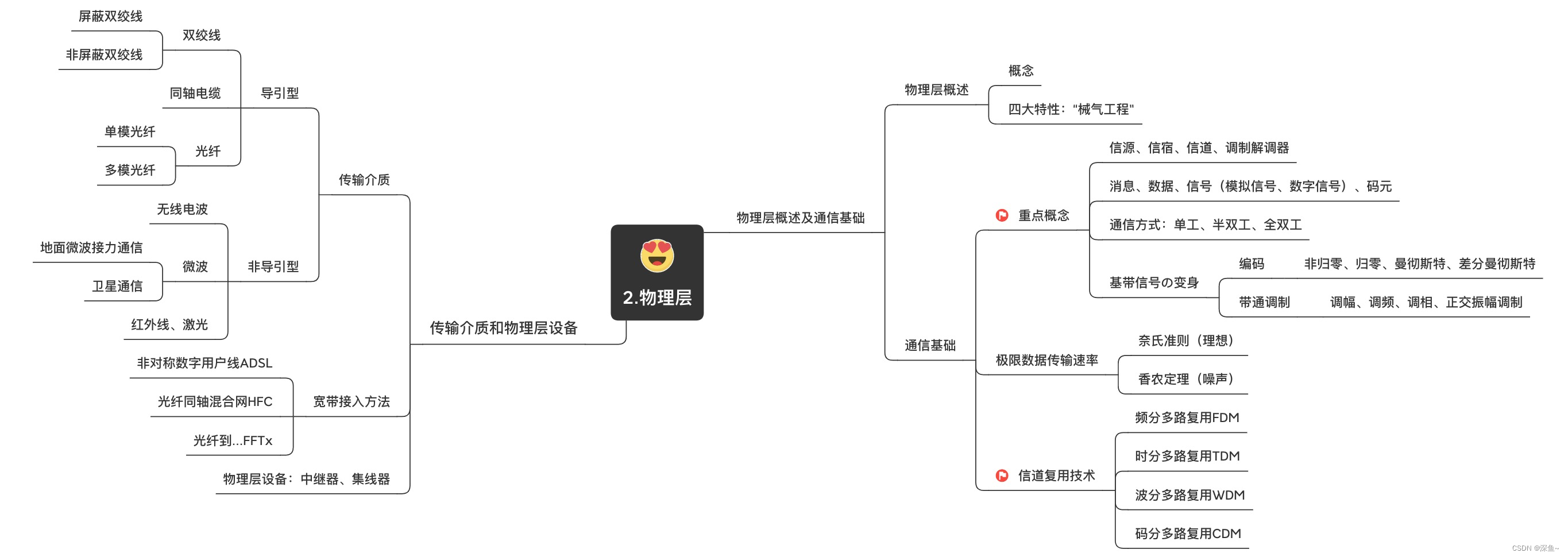
【计算机网络】物理层|传输介质|物理层设备|宽带接入技术
目录 一、思维导图 二、传输介质 1.传输介质——导引型 2.传输介质——非导引型编辑 三、物理层设备 1.物理层设备:中继器&集线器 2.宽带接入技术(有线) 编辑 四、趁热打铁☞习题训练 五、物理层总思维导图 推荐 前些天发现…...

TCP和UDP面试题提问
TOC TCP(传输控制协议)和UDP(用户数据报协议)是两种计算机网络通信协议,它们在网络通信中起着不同的作用。 TCP TCP 是面向连接的协议,它在数据传输之前需要在发送端和接收端建立一条连接。TCP 提供可靠…...

网安常用的三个攻击方式
1.渗透测试执行标准(PTES) 渗透测试执行标准由7个部分组成,包括前期交互、情报收集、威胁建模、漏洞分析、渗透利用、后渗透、撰写报告。在中国,渗透测试必须经过授权,否则就违背了网络安全法。前期交互主要指开展渗透…...

C++面向对象程序设计-北京大学-郭炜【课程笔记(二)】
C面向对象程序设计-北京大学-郭炜【课程笔记(二)】 1、结构化程序设计结构化程序设计的不足 2、面向对象的程序设计2.1、面向对象的程序设计2.2、从客观事物抽象出类2.3、对象的内存分配2.4、对象之间的运算2.5、使用类的成员变量和成员函数用法1&#x…...
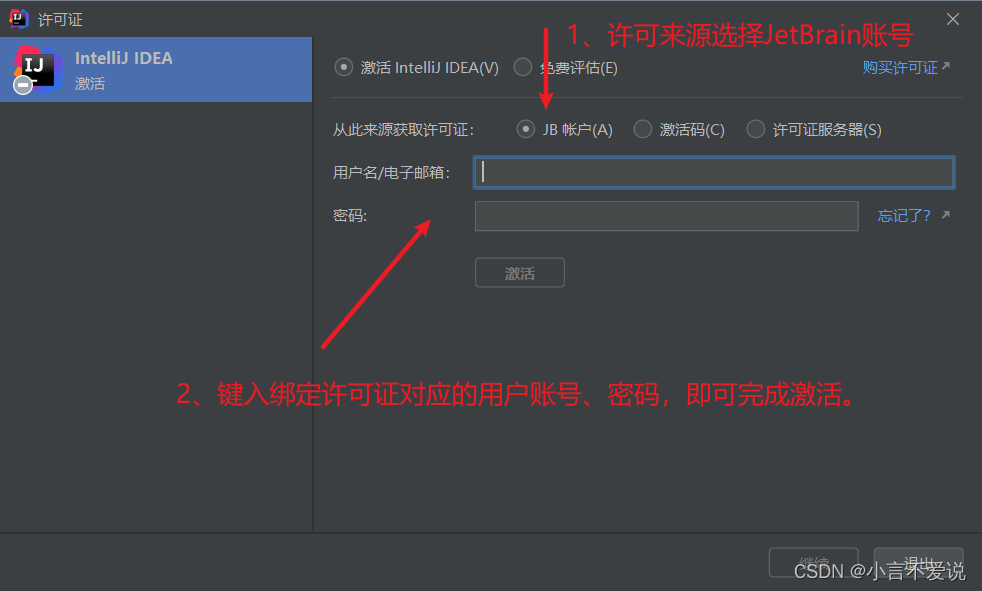
IDEA Ultimate下载(采用JetBrain学生认证)
IDEA Ultimate版本下载 Ulitmate是无限制版(解锁所有插件,正版需要付费。学生可以免费申请许可)Community是开源社区版本(部分插件不提供使用,比如Tomcat插件。免费) 我们将通过学生认证获取免费版。 Je…...

Matplotlib plt.plot数据可视化应用案例
Matplotlib 是 Python 中一个非常流行的绘图库,它允许用户创建各种静态、动态、交互式的图表和可视化。plt.plot() 是 Matplotlib 中用于绘制二维数据的基本函数。 下面是一个使用 plt.plot() 的简单数据可视化应用案例: 案例:绘制正弦和余…...

ES实战--集群扩展
查看ES集群状态: GET /_cluster/health?prettytrue当一个节点加入集群的时候,ES会自动地尝试将分片在所有节点上进行均匀分配. 如果更多的节点加入集群,ES将试图在所有节点上均匀分配分片数量.这样每一个新加入的节点都能通过部分数据来分担负载 第二个节点发现第一个节点,并…...

【重要】django默认生成的表的意思记录
accounts_userprofile: 这是与用户相关的个人资料表,通常包含用户的额外信息,比如头像、个人描述等。 accounts_userprofile_groups: 这是用户个人资料和用户组之间的关联表,用于记录用户属于哪些用户组。 accounts_userprofile_user_permiss…...

12.3 OpenGL顶点后处理:平面着色
平面着色 Flatshading Flat shading (平面着色)是一种简化渲染技术,它在光栅化阶段将一个图元(primitive)的所有顶点赋予相同的颜色或其它输出变量的值。这些赋予的值来自于该图元的“引发顶点”(provoking vertex)。…...

实验5-6 使用函数判断完全平方数
本题要求实现一个判断整数是否为完全平方数的简单函数。 函数接口定义: int IsSquare( int n ); 其中n是用户传入的参数,在长整型范围内。如果n是完全平方数,则函数IsSquare必须返回1,否则返回0。 裁判测试程序样例࿱…...

AI 或许真的能助力中产阶级重塑辉煌 [译]
原文:AI Could Actually Help Rebuild The Middle Class 作者:DAVID AUTOR 译文:AI 或许真的能助力中产阶级重塑辉煌 作者:宝玉 人工智能(AI)并不一定会夺走我们的工作。相反,它为我们提供了一个…...
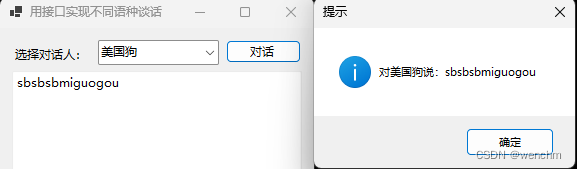
C#利用接口实现选择不同的语种
目录 一、涉及到的知识点 1.接口定义 2.接口具有的特征 3.接口通过类继承来实现 4.有效使用接口进行组件编程 5.Encoding.GetBytes(String)方法 (1)检查给定字符串中是否包含中文字符 (2)编码和还原前后 6.Encoding.GetS…...

设计模式-适配器模式 Adapter
适配器模式 (Adapter) (重点) 适配器设计模式(Adapter Design Pattern)是一种结构型设计模式,用于解决两个不兼容接口之间的问题。适配器允许将一个类的接口转换为客户端期望的另一个接口,使得原本由于接口不兼容而不能一起工作的…...

算法训练day29Leetcode491递增子序列46全排列47全排列Ⅱ
491 递增子序列 题目描述 给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。 数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一…...

内网穿透与搭建私人服务器
前言 内网穿透是一种技术,允许用户从外部网络访问内部私有网络中的服务器或设备。这对于想要从任何地方访问家中或办公室内部网络资源的用户非常有用。以下是为初学者准备的关于如何实现内网穿透以及搭建自己的私人服务器的详细指南。 在这个数字化时代,…...

交大论文下载器
原作者地址: https://github.com/olixu/SJTU_Thesis_Crawler 问题: http://thesis.lib.sjtu.edu.cn/的学位论文下载系统,该版权保护系统用起来很不方便,加载起来非常慢,所以该下载器实现将网页上的每一页的图片合并…...
)
全栈笔记_浏览器扩展篇(manifest.json文件介绍)
manifest.json介绍 是web扩展技术必不可少的插件配置文件,放在根目录作用: 指定插件的基本信息 name:名称manifest_version:manifest.json文件的版本号,可以写2或3version:版本description:描述定义插件的行为: browser_action:添加一个操作按钮到浏览器工具栏,点击按…...
)
蓝桥杯每日一题(python)
##斐波那契数列的应用 --- 题目斐波那契 题目: 如果数组 A (a0, a1, , an−1) 满足以下条件,就说它是一个斐波那契数组: 1. n ≥ 2; 2. a0 a1; 3. 对于所有的 i(i ≥ 2),都满足 ai ai−1 ai−2…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

基于Uniapp的HarmonyOS 5.0体育应用开发攻略
一、技术架构设计 1.混合开发框架选型 (1)使用Uniapp 3.8版本支持ArkTS编译 (2)通过uni-harmony插件调用原生能力 (3)分层架构设计: graph TDA[UI层] -->|Vue语法| B(Uniapp框架)B --&g…...

第22节 Node.js JXcore 打包
Node.js是一个开放源代码、跨平台的、用于服务器端和网络应用的运行环境。 JXcore是一个支持多线程的 Node.js 发行版本,基本不需要对你现有的代码做任何改动就可以直接线程安全地以多线程运行。 本文主要介绍JXcore的打包功能。 JXcore 安装 下载JXcore安装包&a…...

