树形dp 笔记
树的最长路径
给定一棵树,树中包含 n 个结点(编号1~n)和 n−1 条无向边,每条边都有一个权值。
现在请你找到树中的一条最长路径。
换句话说,要找到一条路径,使得使得路径两端的点的距离最远。
注意:路径中可以只包含一个点。
输入格式
第一行包含整数 n。
接下来 n−1 行,每行包含三个整数 ai,bi,ci,表示点 ai 和 bi 之间存在一条权值为 ci 的边。
输出格式
输出一个整数,表示树的最长路径的长度。
数据范围
1≤n≤10000,
1≤ai,bi≤n,
−1e5≤ci≤1e5
输入样例:
6
5 1 6
1 4 5
6 3 9
2 6 8
6 1 7
输出样例:
22边权不为负可以用两次dfs,边权有负就要用这种了
一个点选两个能走得贡献最大的孩子,相加就是能搭在这个点上最长的直径,所有点跑一遍,找最长的那个就行
理论上一个直径上每个点算出来的值都不一样,因为dfs得有个顺序,都是父亲向孩子走得,但每条直径都一定会被算到。
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 20010;int pos, n;
int h[N], e[N], w[N], ne[N], idx;
int ans;void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}int dfs(int u, int father)
{int dist = 0;int d1 = 0, d2 = 0;for(int i = h[u]; i != -1; i = ne[i]){int j = e[i];if(j == father)continue;int d = dfs(j, u) + w[i];dist = max(dist, d);if(d > d1)d2 = d1, d1 = d;else if(d > d2)d2 = d;}ans = max(ans, d1 + d2);return dist;
}int main()
{IOScin >> n;memset(h, -1, sizeof h);for(int i = 1; i < n; i ++){int a, b, c;cin >> a >> b >> c;add(a, b, c);add(b, a, c);}dfs(1, -1);cout << ans;return 0;
}树的中心
给定一棵树,树中包含 n个结点(编号1~n)和 n−1 条无向边,每条边都有一个权值。
请你在树中找到一个点,使得该点到树中其他结点的最远距离最近。
输入格式
第一行包含整数 n。
接下来 n−1 行,每行包含三个整数 ai,bi,ci,表示点 ai 和 bi 之间存在一条权值为 ci 的边。
输出格式
输出一个整数,表示所求点到树中其他结点的最远距离。
数据范围
1≤n≤10000,
1≤ai,bi≤n,
1≤ci≤1e5
输入样例:
5
2 1 1
3 2 1
4 3 1
5 1 1
输出样例:
2可以延续上一题的思路,尝试枚举一下每个点
最远距离除了往下走的还有一条往上走的,要在两者中取一个最大值
dist数组存往下走的最大值,up数组存往上走的最大值
第一次dfs可以求出dist数组的每个值
然后第二次dfs可以用dist数组的值退出来up的值,根节点up为0,然后就可以按dfs顺序递推出来孩子的up的值了。
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 20010;int pos, n;
int h[N], e[N], w[N], ne[N], idx;
int dist[N], up[N];
int ans = 2e9;void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}int dfs(int u, int father)
{int res = 0;for(int i = h[u]; i != -1; i = ne[i]){int j = e[i];if(j == father)continue;int d = dfs(j, u) + w[i];res = max(res, d);}dist[u] = res;return res;
}void dfs1(int u, int father)
{int d1 = 0, d2 = 0;for(int i = h[u]; i != -1; i = ne[i]){int j = e[i];if(j == father)continue;int d = dist[j] + w[i];if(d > d1)d2 = d1, d1 = d;else if(d > d2)d2 = d;}if(up[u] > d1)d2 = d1, d1 = up[u];else if(up[u] > d2)d2 = up[u];for(int i = h[u]; i != -1; i = ne[i]){int j = e[i];if(j == father)continue;int res;if(dist[j] + w[i] == d1)res = d2;else res = d1;up[j] = res + w[i];int tmp = max(up[j], dist[j]);ans = min(ans, tmp);dfs1(j, u);}
}int main()
{IOScin >> n;memset(h, -1, sizeof h);for(int i = 1; i < n; i ++){int a, b, c;cin >> a >> b >> c;add(a, b, c);add(b, a, c);}dfs(1, -1);dfs1(1, -1);ans = min(ans, dist[1]);cout << ans;return 0;
}数字转换
如果一个数 x 的约数之和 y(不包括他本身)比他本身小,那么 x 可以变成 y,y 也可以变成 x。
例如,4 可以变为 3,1 可以变为 7。
限定所有数字变换在不超过 n 的正整数范围内进行,求不断进行数字变换且不出现重复数字的最多变换步数。
输入格式
输入一个正整数 n。
输出格式
输出不断进行数字变换且不出现重复数字的最多变换步数。
数据范围
1≤n≤50000
输入样例:
7
输出样例:
3
样例解释
一种方案为:4→3→1→7。
可以把每个数字看成一个点,求得问题转换为求树的直径
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 50010;int n;
vector<int> g[N];
int ans;
bool st[N];
int sum[N];int get(int x)
{int res = 1;for(int i = 2; i * i <= x; i ++){if(x % i == 0){res += i;if(x / i != i)res += x / i;}}return res;
}int dfs(int u, int father)
{int d1 = 0, d2 = 0;for(auto j : g[u]){if(j == father)continue;int d = dfs(j, u) + 1;if(d > d1)d2 = d1, d1 = d;else if(d > d2)d2 = d;}ans = max(ans, d1 + d2);return d1;
}int main()
{IOScin >> n;for (int i = 1; i <= n; i ++)for (int j = 2; j <= n / i; j ++)sum[i * j] += i;for (int i = 2; i <= n; i ++)if (sum[i] < i){g[sum[i]].push_back(i);g[i].push_back(sum[i]);}dfs(1, -1);cout << ans;return 0;
}二叉苹果树
有一棵二叉苹果树,如果树枝有分叉,一定是分两叉,即没有只有一个儿子的节点。
这棵树共 N 个节点,编号为 1 至 N,树根编号一定为 1。
我们用一根树枝两端连接的节点编号描述一根树枝的位置。
一棵苹果树的树枝太多了,需要剪枝。但是一些树枝上长有苹果,给定需要保留的树枝数量,求最多能留住多少苹果。
这里的保留是指最终与1号点连通。
输入格式
第一行包含两个整数 N 和 Q,分别表示树的节点数以及要保留的树枝数量。
接下来 N−1 行描述树枝信息,每行三个整数,前两个是它连接的节点的编号,第三个数是这根树枝上苹果数量。
输出格式
输出仅一行,表示最多能留住的苹果的数量。
数据范围
1≤Q<N≤100.
N≠1,
每根树枝上苹果不超过 30000个。
输入样例:
5 2
1 3 1
1 4 10
2 3 20
3 5 20
输出样例:
21有依赖的背包问题的简化版
f[u][j]表示节点u,可分配树枝数量为j,最大值 (j也可理解为背包容量,但也有点不一样,这个容量不包括本身在内)
理解写在注释里了
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 110, M = 210;int n, m;
int h[N], e[M], w[M], ne[M], idx;
int f[N][N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}void dfs(int u, int father)
{for(int i = h[u]; i != -1; i = ne[i])//第i个物品组{//int j = e[i];if(e[i] == father)continue;dfs(e[i], u);for(int j = m; j >= 0; j --)//背包容量{for(int k = 0; k < j; k ++)//不同决策{f[u][j] = max(f[u][j], f[u][j - k - 1] + f[e[i]][k] + w[i]);//分组背包是物品组里的每个物品体积和价值不同// f[u][i-1][j] f[u][i-1][j-vk] + w}}}
}int main()
{IOSmemset(h, -1, sizeof h);cin >> n >> m;for(int i = 1; i < n; i ++){int a, b, c;cin >> a >> b >> c;add(a, b, c), add(b, a, c);}dfs(1, -1);cout << f[1][m];return 0;
}战略游戏
鲍勃喜欢玩电脑游戏,特别是战略游戏,但有时他找不到解决问题的方法,这让他很伤心。
现在他有以下问题。
他必须保护一座中世纪城市,这条城市的道路构成了一棵树。
每个节点上的士兵可以观察到所有和这个点相连的边。
他必须在节点上放置最少数量的士兵,以便他们可以观察到所有的边。
你能帮助他吗?
例如,下面的树:
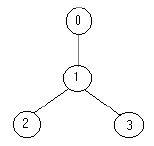
只需要放置 1 名士兵(在节点 1 处),就可观察到所有的边。
输入格式
输入包含多组测试数据,每组测试数据用以描述一棵树。
对于每组测试数据,第一行包含整数 N,表示树的节点数目。
接下来 N 行,每行按如下方法描述一个节点。
节点编号:(子节点数目) 子节点 子节点 …
节点编号从 0 到 N−1,每个节点的子节点数量均不超过 10,每个边在输入数据中只出现一次。
输出格式
对于每组测试数据,输出一个占据一行的结果,表示最少需要的士兵数。
数据范围
0<N≤1500,
一个测试点所有 N 相加之和不超过 300650。
输入样例:
4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)
输出样例:
1
2
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 1510;int n;
vector<int> g[N];
int d[N];
int f[N][2];void dfs(int u)
{f[u][0] = 0;f[u][1] = 1;for(auto j : g[u]){dfs(j);f[u][0] += f[j][1];f[u][1] += min(f[j][0], f[j][1]);}
}int main()
{IOSwhile(cin >> n){for(int i = 0; i <= n; i ++){g[i].clear();d[i] = 0;f[i][0] = f[i][1] = 0;}int ver1, ver2, num;char tmp;for(int i = 0; i < n; i ++){cin >> ver1 >>tmp >> tmp >> num >> tmp;for(int i = 0; i < num; i ++){cin >> ver2;g[ver1].push_back(ver2);d[ver2] ++;}}int root;for(int i = 0; i < n; i ++){if(!d[i]){root = i;break;}}dfs(root);cout << min(f[root][0], f[root][1]) << endl;}return 0;
}皇宫看守
太平王世子事件后,陆小凤成了皇上特聘的御前一品侍卫。
皇宫各个宫殿的分布,呈一棵树的形状,宫殿可视为树中结点,两个宫殿之间如果存在道路直接相连,则该道路视为树中的一条边。
已知,在一个宫殿镇守的守卫不仅能够观察到本宫殿的状况,还能观察到与该宫殿直接存在道路相连的其他宫殿的状况。
大内保卫森严,三步一岗,五步一哨,每个宫殿都要有人全天候看守,在不同的宫殿安排看守所需的费用不同。
可是陆小凤手上的经费不足,无论如何也没法在每个宫殿都安置留守侍卫。
帮助陆小凤布置侍卫,在看守全部宫殿的前提下,使得花费的经费最少。
输入格式
输入中数据描述一棵树,描述如下:
第一行 n,表示树中结点的数目。
第二行至第 n+1 行,每行描述每个宫殿结点信息,依次为:该宫殿结点标号 i,在该宫殿安置侍卫所需的经费 k,该结点的子结点数 m,接下来 m 个数,分别是这个结点的 m 个子结点的标号 r1,r2,…,rm。
对于一个 n 个结点的树,结点标号在 1 到 n 之间,且标号不重复。
输出格式
输出一个整数,表示最少的经费。
数据范围
1≤n≤1500
输入样例:
6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0
输出样例:
25
样例解释:
在2、3、4结点安排护卫,可以观察到全部宫殿,所需经费最少,为 16 + 5 + 4 = 25。
本来以为和上一题差不多结果wa了
发现有一种情况是上一题没有的:
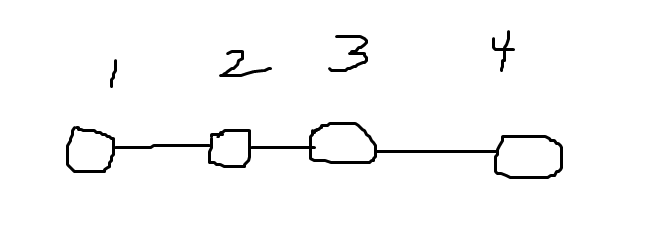
选1、4点也是符合要求的
f[u][0] 不放,但能被父节点看到
f[u][1] 不放,但能被子节点看到
f[u][2] 放
f[u][0]和f[u][2]都很好像,主要是如何得到f[u][1],能被子节点看到,那就选能被哪个子节点看到,其他点取min(f[u][1], f[u][2]),在所有方案中选个最小值
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 1510;int n;
vector<int> g[N];
int w[N], d[N];
int f[N][3];
//f[u][0] 不放,但能被父节点看到
//f[u][1] 不放,但能被子节点看到
//f[u][2] 放 void dfs(int u)
{f[u][0] = 0, f[u][1] = 0, f[u][2] = w[u];int sum = 0;for(auto j : g[u]){dfs(j);f[u][0] += min(f[j][1], f[j][2]);sum += min(f[j][1], f[j][2]);f[u][2] += min(min(f[j][0], f[j][1]), f[j][2]);}int res = 2e9;for(auto j : g[u]){res = min(res, sum + f[j][2] - min(f[j][1], f[j][2]));}f[u][1] = res;
}int main()
{IOScin >> n;for(int i = 0; i < n; i ++){int id, val, num;cin >> id >> val >> num;w[id] = val;for(int j = 0; j < num; j ++){int x;cin >> x;d[x] ++;g[id].push_back(x);}}int root;for(int i = 1; i <= n; i ++){if(!d[i]){root = i;break;}}dfs(root);cout << min(f[root][1], f[root][2]);return 0;
}相关文章:

树形dp 笔记
树的最长路径 给定一棵树,树中包含 n 个结点(编号1~n)和 n−1 条无向边,每条边都有一个权值。 现在请你找到树中的一条最长路径。 换句话说,要找到一条路径,使得使得路径两端的点的距离最远。 注意&…...
2024-02-08 Unity 编辑器开发之编辑器拓展1 —— 自定义菜单栏
文章目录 1 特殊文件夹 Editor2 在 Unity 菜单栏中添加自定义页签3 在 Hierarchy 窗口中添加自定义页签4 在 Project 窗口中添加自定义页签5 在菜单栏的 Component 菜单添加脚本6 在 Inspector 为脚本右键添加菜单7 加入快捷键8 小结 1 特殊文件夹 Editor Editor 文件夹是 …...

typescript中的Omit排除类型及Pick取想要的属性
Omit 的使用:排除类型 type OmitUser {name: string,age: number,sex:string } type newOmit Omit<OmitUser, sex>// 定义一个对象并将其类型设置为 newOmit const example: newOmit {name: "John",age: 30 };console.log( Omit 的使用:排除类型 , example…...
MATLAB计算极限和微积分
一.函数与极限 计算极限:lim(3*x^2/(2x1)),x分别趋于0和1,代码如下: syms x; limit(3*x*x/(2*x1),x,0) limit(3*x*x/(2*x1),x,1) 结果分别为0和1: 1.计算双侧极限 计算极限:lim(3*x^2/(2x1))࿰…...

在数组中插入元素
问题:假设有一个数组{1,2,3,4,5},如果我们要在3之后插入一个数(520),这该怎么办呢? 思路:要想在以元素3之后插入一个元素,我们先要做…...
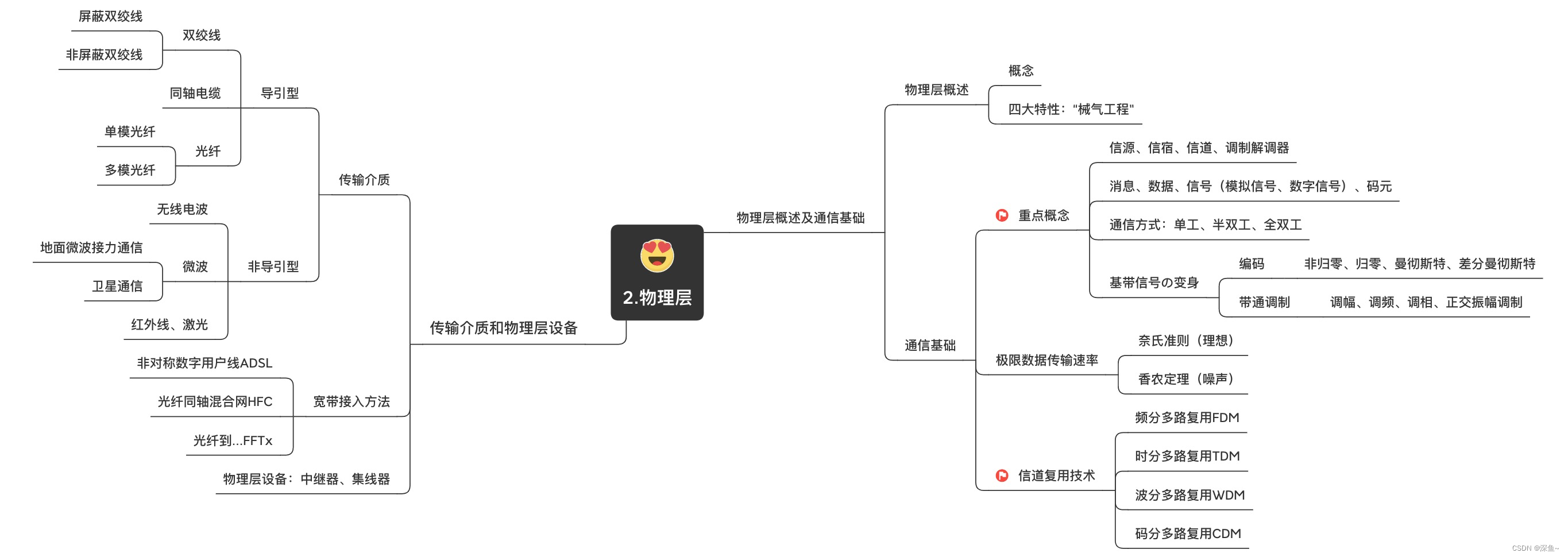
【计算机网络】物理层|传输介质|物理层设备|宽带接入技术
目录 一、思维导图 二、传输介质 1.传输介质——导引型 2.传输介质——非导引型编辑 三、物理层设备 1.物理层设备:中继器&集线器 2.宽带接入技术(有线) 编辑 四、趁热打铁☞习题训练 五、物理层总思维导图 推荐 前些天发现…...

TCP和UDP面试题提问
TOC TCP(传输控制协议)和UDP(用户数据报协议)是两种计算机网络通信协议,它们在网络通信中起着不同的作用。 TCP TCP 是面向连接的协议,它在数据传输之前需要在发送端和接收端建立一条连接。TCP 提供可靠…...

网安常用的三个攻击方式
1.渗透测试执行标准(PTES) 渗透测试执行标准由7个部分组成,包括前期交互、情报收集、威胁建模、漏洞分析、渗透利用、后渗透、撰写报告。在中国,渗透测试必须经过授权,否则就违背了网络安全法。前期交互主要指开展渗透…...

C++面向对象程序设计-北京大学-郭炜【课程笔记(二)】
C面向对象程序设计-北京大学-郭炜【课程笔记(二)】 1、结构化程序设计结构化程序设计的不足 2、面向对象的程序设计2.1、面向对象的程序设计2.2、从客观事物抽象出类2.3、对象的内存分配2.4、对象之间的运算2.5、使用类的成员变量和成员函数用法1&#x…...
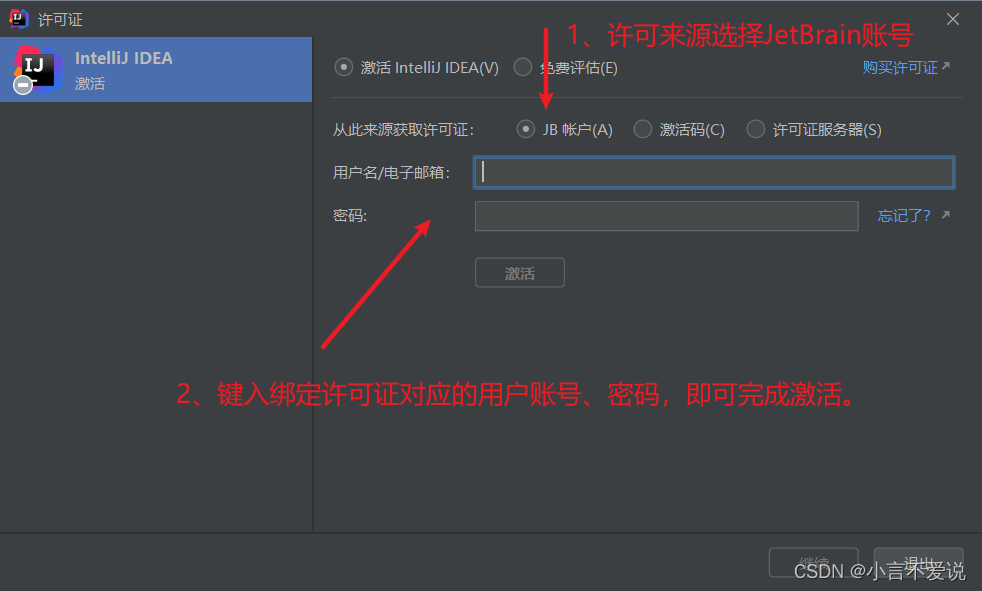
IDEA Ultimate下载(采用JetBrain学生认证)
IDEA Ultimate版本下载 Ulitmate是无限制版(解锁所有插件,正版需要付费。学生可以免费申请许可)Community是开源社区版本(部分插件不提供使用,比如Tomcat插件。免费) 我们将通过学生认证获取免费版。 Je…...

Matplotlib plt.plot数据可视化应用案例
Matplotlib 是 Python 中一个非常流行的绘图库,它允许用户创建各种静态、动态、交互式的图表和可视化。plt.plot() 是 Matplotlib 中用于绘制二维数据的基本函数。 下面是一个使用 plt.plot() 的简单数据可视化应用案例: 案例:绘制正弦和余…...

ES实战--集群扩展
查看ES集群状态: GET /_cluster/health?prettytrue当一个节点加入集群的时候,ES会自动地尝试将分片在所有节点上进行均匀分配. 如果更多的节点加入集群,ES将试图在所有节点上均匀分配分片数量.这样每一个新加入的节点都能通过部分数据来分担负载 第二个节点发现第一个节点,并…...

【重要】django默认生成的表的意思记录
accounts_userprofile: 这是与用户相关的个人资料表,通常包含用户的额外信息,比如头像、个人描述等。 accounts_userprofile_groups: 这是用户个人资料和用户组之间的关联表,用于记录用户属于哪些用户组。 accounts_userprofile_user_permiss…...

12.3 OpenGL顶点后处理:平面着色
平面着色 Flatshading Flat shading (平面着色)是一种简化渲染技术,它在光栅化阶段将一个图元(primitive)的所有顶点赋予相同的颜色或其它输出变量的值。这些赋予的值来自于该图元的“引发顶点”(provoking vertex)。…...

实验5-6 使用函数判断完全平方数
本题要求实现一个判断整数是否为完全平方数的简单函数。 函数接口定义: int IsSquare( int n ); 其中n是用户传入的参数,在长整型范围内。如果n是完全平方数,则函数IsSquare必须返回1,否则返回0。 裁判测试程序样例࿱…...

AI 或许真的能助力中产阶级重塑辉煌 [译]
原文:AI Could Actually Help Rebuild The Middle Class 作者:DAVID AUTOR 译文:AI 或许真的能助力中产阶级重塑辉煌 作者:宝玉 人工智能(AI)并不一定会夺走我们的工作。相反,它为我们提供了一个…...
C#利用接口实现选择不同的语种
目录 一、涉及到的知识点 1.接口定义 2.接口具有的特征 3.接口通过类继承来实现 4.有效使用接口进行组件编程 5.Encoding.GetBytes(String)方法 (1)检查给定字符串中是否包含中文字符 (2)编码和还原前后 6.Encoding.GetS…...

设计模式-适配器模式 Adapter
适配器模式 (Adapter) (重点) 适配器设计模式(Adapter Design Pattern)是一种结构型设计模式,用于解决两个不兼容接口之间的问题。适配器允许将一个类的接口转换为客户端期望的另一个接口,使得原本由于接口不兼容而不能一起工作的…...

算法训练day29Leetcode491递增子序列46全排列47全排列Ⅱ
491 递增子序列 题目描述 给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。 数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一…...

内网穿透与搭建私人服务器
前言 内网穿透是一种技术,允许用户从外部网络访问内部私有网络中的服务器或设备。这对于想要从任何地方访问家中或办公室内部网络资源的用户非常有用。以下是为初学者准备的关于如何实现内网穿透以及搭建自己的私人服务器的详细指南。 在这个数字化时代,…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...
