TestNG invocationCount属性
有时我们会遇到这样的问题,比如如何多次运行一个测试用例?invocationCount是这个问题的答案。在这篇文章中,我们将讨论在TestNG中与@Test annotation一起使用的invocationCount属性。
这个属性有什么作用,或者调用计数有什么用?invocationCount有助于多次执行单个测试用例。因此,如果您有一个需要多次运行的测试用例,invocationCount可以帮助您。
语法
@Test(invocationCount = num)其中num =您希望运行此测试方法的次数。
示例:
package Test;import org.testng.Assert;
import org.testng.annotations.Test;public class CodekruTest {@Test(invocationCount = 5) // now, this test case will run 5 timespublic void test2() {System.out.println("test2 is passed");Assert.assertTrue(true);}}下面是运行上述测试类的XML文件
<suite name="codekru"><test name="codekruTest"><classes><class name="Test.CodekruTest"></class></classes></test>
</suite>运行上述XML文件后的输出-
test2 is passed
test2 is passed
test2 is passed
test2 is passed
test2 is passed
PASSED: test2
PASSED: test2
PASSED: test2
PASSED: test2
PASSED: test2===============================================Default testTests run: 5, Failures: 0, Skips: 0
===============================================所以,在这里我们可以看到test()运行了五次。
假设情景
如果我们保持invocationCount =0呢?到时候会发生什么?
在这里,测试用例甚至不会运行,如下面的示例所示
package Test;import org.testng.Assert;
import org.testng.annotations.Test;public class CodekruTest {@Test(invocationCount = 0) // now, this test case will run 5 timespublic void test2() {System.out.println("test2 is passed");Assert.assertTrue(true);}}运行相同的XML文件后的输出-
===============================================
codekru
Total tests run: 0, Passes: 0, Failures: 0, Skips: 0
===============================================在这里我们可以看到没有执行任何测试用例或方法。
如果我们将invocationCount保持为负值呢?
它不会给予任何错误,但是测试用例不会被执行。
package Test;import org.testng.Assert;
import org.testng.annotations.Test;public class CodekruTest {@Test(invocationCount = -2) // now, this test case will run 5 timespublic void test2() {System.out.println("test2 is passed");Assert.assertTrue(true);}}产出-
===============================================
codekru
Total tests run: 0, Passes: 0, Failures: 0, Skips: 0
===============================================相关文章:

TestNG invocationCount属性
有时我们会遇到这样的问题,比如如何多次运行一个测试用例?invocationCount是这个问题的答案。在这篇文章中,我们将讨论在TestNG中与Test annotation一起使用的invocationCount属性。 这个属性有什么作用,或者调用计数有什么用&am…...

关于maven项目中无法通过邮件服务器发送邮件的补充解决方案
1、问题及解决方法 我的一篇文章中提到使用代码发送电子邮件,但是maven项目中无法执行成功,现在我找到了解决办法,只要引入依赖时同时引入下面两个依赖就行了,我无法找到原因主要是使用单元测试方法运行,它居然不报错&…...
树形dp 笔记
树的最长路径 给定一棵树,树中包含 n 个结点(编号1~n)和 n−1 条无向边,每条边都有一个权值。 现在请你找到树中的一条最长路径。 换句话说,要找到一条路径,使得使得路径两端的点的距离最远。 注意&…...
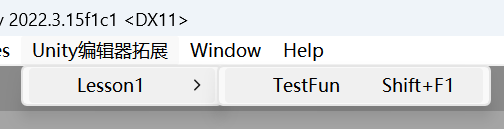
2024-02-08 Unity 编辑器开发之编辑器拓展1 —— 自定义菜单栏
文章目录 1 特殊文件夹 Editor2 在 Unity 菜单栏中添加自定义页签3 在 Hierarchy 窗口中添加自定义页签4 在 Project 窗口中添加自定义页签5 在菜单栏的 Component 菜单添加脚本6 在 Inspector 为脚本右键添加菜单7 加入快捷键8 小结 1 特殊文件夹 Editor Editor 文件夹是 …...

typescript中的Omit排除类型及Pick取想要的属性
Omit 的使用:排除类型 type OmitUser {name: string,age: number,sex:string } type newOmit Omit<OmitUser, sex>// 定义一个对象并将其类型设置为 newOmit const example: newOmit {name: "John",age: 30 };console.log( Omit 的使用:排除类型 , example…...
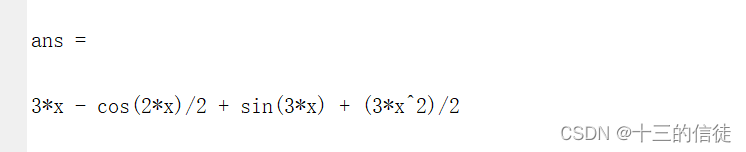
MATLAB计算极限和微积分
一.函数与极限 计算极限:lim(3*x^2/(2x1)),x分别趋于0和1,代码如下: syms x; limit(3*x*x/(2*x1),x,0) limit(3*x*x/(2*x1),x,1) 结果分别为0和1: 1.计算双侧极限 计算极限:lim(3*x^2/(2x1))࿰…...

在数组中插入元素
问题:假设有一个数组{1,2,3,4,5},如果我们要在3之后插入一个数(520),这该怎么办呢? 思路:要想在以元素3之后插入一个元素,我们先要做…...
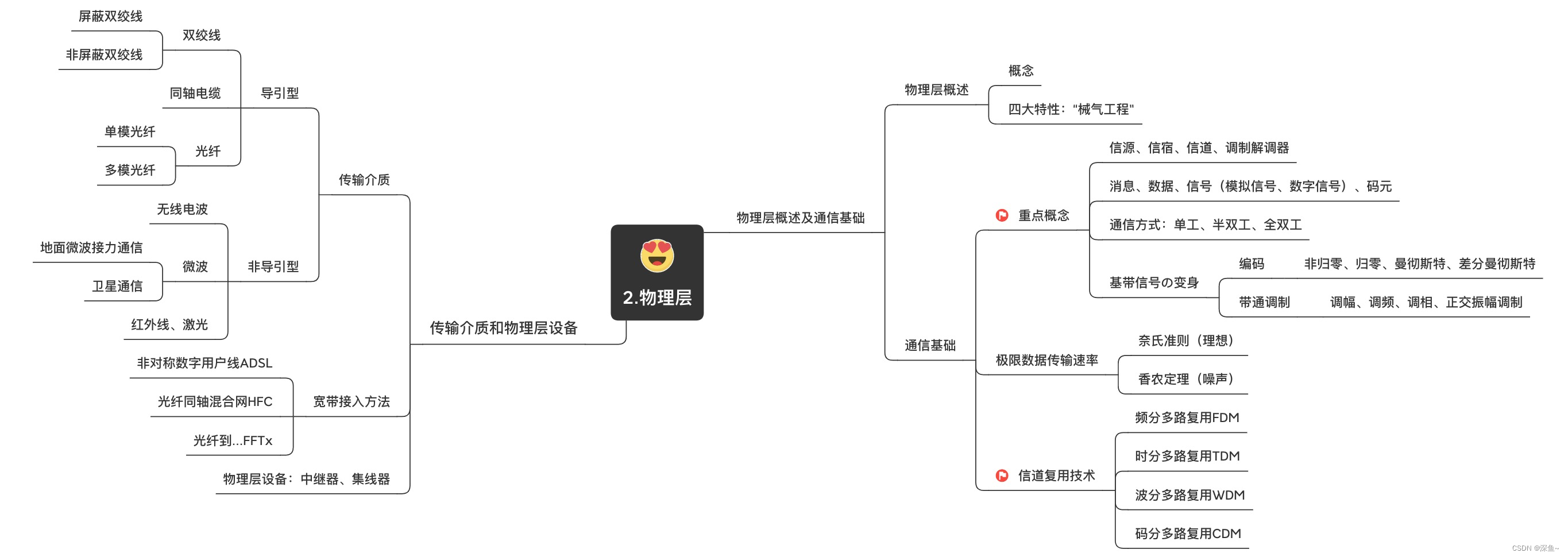
【计算机网络】物理层|传输介质|物理层设备|宽带接入技术
目录 一、思维导图 二、传输介质 1.传输介质——导引型 2.传输介质——非导引型编辑 三、物理层设备 1.物理层设备:中继器&集线器 2.宽带接入技术(有线) 编辑 四、趁热打铁☞习题训练 五、物理层总思维导图 推荐 前些天发现…...

TCP和UDP面试题提问
TOC TCP(传输控制协议)和UDP(用户数据报协议)是两种计算机网络通信协议,它们在网络通信中起着不同的作用。 TCP TCP 是面向连接的协议,它在数据传输之前需要在发送端和接收端建立一条连接。TCP 提供可靠…...

网安常用的三个攻击方式
1.渗透测试执行标准(PTES) 渗透测试执行标准由7个部分组成,包括前期交互、情报收集、威胁建模、漏洞分析、渗透利用、后渗透、撰写报告。在中国,渗透测试必须经过授权,否则就违背了网络安全法。前期交互主要指开展渗透…...

C++面向对象程序设计-北京大学-郭炜【课程笔记(二)】
C面向对象程序设计-北京大学-郭炜【课程笔记(二)】 1、结构化程序设计结构化程序设计的不足 2、面向对象的程序设计2.1、面向对象的程序设计2.2、从客观事物抽象出类2.3、对象的内存分配2.4、对象之间的运算2.5、使用类的成员变量和成员函数用法1&#x…...
IDEA Ultimate下载(采用JetBrain学生认证)
IDEA Ultimate版本下载 Ulitmate是无限制版(解锁所有插件,正版需要付费。学生可以免费申请许可)Community是开源社区版本(部分插件不提供使用,比如Tomcat插件。免费) 我们将通过学生认证获取免费版。 Je…...

Matplotlib plt.plot数据可视化应用案例
Matplotlib 是 Python 中一个非常流行的绘图库,它允许用户创建各种静态、动态、交互式的图表和可视化。plt.plot() 是 Matplotlib 中用于绘制二维数据的基本函数。 下面是一个使用 plt.plot() 的简单数据可视化应用案例: 案例:绘制正弦和余…...

ES实战--集群扩展
查看ES集群状态: GET /_cluster/health?prettytrue当一个节点加入集群的时候,ES会自动地尝试将分片在所有节点上进行均匀分配. 如果更多的节点加入集群,ES将试图在所有节点上均匀分配分片数量.这样每一个新加入的节点都能通过部分数据来分担负载 第二个节点发现第一个节点,并…...

【重要】django默认生成的表的意思记录
accounts_userprofile: 这是与用户相关的个人资料表,通常包含用户的额外信息,比如头像、个人描述等。 accounts_userprofile_groups: 这是用户个人资料和用户组之间的关联表,用于记录用户属于哪些用户组。 accounts_userprofile_user_permiss…...

12.3 OpenGL顶点后处理:平面着色
平面着色 Flatshading Flat shading (平面着色)是一种简化渲染技术,它在光栅化阶段将一个图元(primitive)的所有顶点赋予相同的颜色或其它输出变量的值。这些赋予的值来自于该图元的“引发顶点”(provoking vertex)。…...

实验5-6 使用函数判断完全平方数
本题要求实现一个判断整数是否为完全平方数的简单函数。 函数接口定义: int IsSquare( int n ); 其中n是用户传入的参数,在长整型范围内。如果n是完全平方数,则函数IsSquare必须返回1,否则返回0。 裁判测试程序样例࿱…...

AI 或许真的能助力中产阶级重塑辉煌 [译]
原文:AI Could Actually Help Rebuild The Middle Class 作者:DAVID AUTOR 译文:AI 或许真的能助力中产阶级重塑辉煌 作者:宝玉 人工智能(AI)并不一定会夺走我们的工作。相反,它为我们提供了一个…...
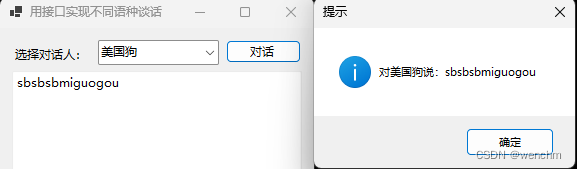
C#利用接口实现选择不同的语种
目录 一、涉及到的知识点 1.接口定义 2.接口具有的特征 3.接口通过类继承来实现 4.有效使用接口进行组件编程 5.Encoding.GetBytes(String)方法 (1)检查给定字符串中是否包含中文字符 (2)编码和还原前后 6.Encoding.GetS…...

设计模式-适配器模式 Adapter
适配器模式 (Adapter) (重点) 适配器设计模式(Adapter Design Pattern)是一种结构型设计模式,用于解决两个不兼容接口之间的问题。适配器允许将一个类的接口转换为客户端期望的另一个接口,使得原本由于接口不兼容而不能一起工作的…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

职坐标物联网全栈开发全流程解析
物联网全栈开发涵盖从物理设备到上层应用的完整技术链路,其核心流程可归纳为四大模块:感知层数据采集、网络层协议交互、平台层资源管理及应用层功能实现。每个模块的技术选型与实现方式直接影响系统性能与扩展性,例如传感器选型需平衡精度与…...

浏览器工作原理01 [#]Chrome架构:仅仅打开了1个页面,为什么有4个进程
引用 浏览器工作原理与实践 Chrome打开一个页面需要启动多少进程?你可以点击Chrome浏览器右上角的“选项”菜单,选择“更多工具”子菜单,点击“任务管理器”,这将打开Chrome的任务管理器的窗口,如下图 和Windows任务管…...
