【机器学习基础】决策树(Decision Tree)
🚀个人主页:为梦而生~ 关注我一起学习吧!
💡专栏:机器学习 欢迎订阅!后面的内容会越来越有意思~
⭐特别提醒:针对机器学习,特别开始专栏:机器学习python实战 欢迎订阅!本专栏针对机器学习基础专栏的理论知识,利用python代码进行实际展示,真正做到从基础到实战!
💡往期推荐:
【机器学习基础】机器学习入门(1)
【机器学习基础】机器学习入门(2)
【机器学习基础】机器学习的基本术语
【机器学习基础】机器学习的模型评估(评估方法及性能度量原理及主要公式)
【机器学习基础】一元线性回归(适合初学者的保姆级文章)
【机器学习基础】多元线性回归(适合初学者的保姆级文章)
【机器学习基础】对数几率回归(logistic回归)
【机器学习基础】正则化
💡本期内容:前面讲了三个最基本的模型,包括了分类和回归,这里再来介绍另外一种很常用的分类方法:决策树。
文章目录
- 1 什么是决策树
- 1.1 决策树的基本描述
- 1.2 决策树的组成
- 1.3 决策树的递归策略
- 2 划分选择
- 2.1 信息熵
- 2.2 信息增益
- 2.3 增益率
- 2.4 基尼指数
- 3 剪枝处理
- 3.1 预剪枝
- 3.1.1 预剪枝的优缺点
- 3.2 后剪枝
- 3.2.1 后剪枝的优缺点
- 4 连续属性处理
- 4.1 连续属性离散化(二分法)
- 5 多变量决策树
- 成熟的决策树软件包
1 什么是决策树
决策树是一种树形结构,用于描述从一组数据中提取出一些特征,并通过这些特征来进行分类或预测的过程。决策树的每个节点表示一个特征,每个分支表示这个特征的一个取值,叶子节点表示最终的分类结果。

1.1 决策树的基本描述
- 决策过程中提出的每个判定问题都是对某个属性的“测试”
- 决策过程的最终结论对应了我们所希望的判定结果
- 每个测试的结果或是导出最终结论,或者导出进一步的判定问题,其考虑范围是在上次决策结果的限定范围之内
- 从根结点到每个叶结点的路径对应了一个判定测试序列
决策树学习的目的是为了产生一棵泛化能力强,即处理未见示例能力强的决策树
1.2 决策树的组成
决策树由以下几部分组成:
- 决策节点:决策树的起点,代表了整个决策过程的开始。
- 机会节点:机会节点代表一个事件发生的可能性,也就是一个随机事件。
- 决策枝:从决策节点或机会节点出发,代表决策者可以作出的选择或决策。
- 概率枝:从机会节点出发,代表该事件发生的概率。
- 损益值:在决策过程中,每个决策或事件的发生都伴随着一定的成本或收益,这些成本或收益被称为损益值。
- 终点:代表了决策过程的结束,通常以一个方框表示。
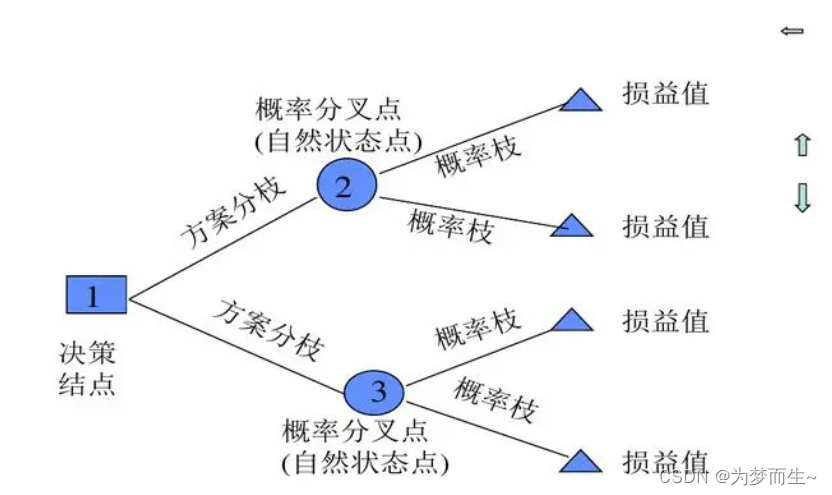
在构建决策树时,需要从决策树的末端开始,从后向前逐步推进到决策树的始端。在推进的过程中,需要计算每个阶段事件发生的期望值,并考虑资金的时间价值。最后,通过对决策树进行剪枝,删去除了最高期望值以外的其他所有分枝,找到问题的最佳方案。
1.3 决策树的递归策略
显然,决策树的生成是一个递归过程。在决策树基本算法中,有三种情形会导致递归返回:
- 当前结点包含的样本全属于同一类别,无需划分
- 当前属性集为空或是所有样本在所有属性上取值相同,无法划分
- 当前结点包含的样本集合为空不能划分

在第(2)种情形下,我们把当前结点标记为叶结点,并将其类别设定为该结点所含样本最多的类别; 在第(3)种情形下,同样把当前结点标记为叶结点,但将其类别设定为其父结点所含样本最多的类别.注意这两种情形的处理实质不同: 情形(2)是在利用当前结点的后验分布而情形(3)则是把结点的样本分布作为当前结点的先验分布.
2 划分选择
决策树的关键是如何选择最优划分属性,一般而言,随着划分过程的不断进行,我们希望决策树的分支节点包含的样本尽可能的属于同一类别,即结点的“纯度”越来越高
2.1 信息熵
在决策树中,信息熵是一个重要的概念,用于度量样本集合的不纯度。对于样本集合而言,如果样本集合中只有一个类别,则其确定性最高,熵为0;反之,如果样本集合中包含多个类别,则熵越大,表示样本集合中的分类越多样。

在决策树的构建过程中,信息熵被用来选择最佳的划分属性。对于每个属性,计算其划分后的信息熵,选择使得信息熵最小的属性作为当前节点的划分属性。这样能够使得划分后的子树更加纯,即类别更加明显,从而降低样本集合的不确定性。
信息熵的公式如下:

假定离散属性 α \alpha α有 V V V个可能的取值,若使用 α \alpha α来对样本集 D D D进行划分,则会产生 V V V个分支结点,其中 v v v第个分支结点包含了 D D D中所有在属性 a a a上取值为 a v a^v av的样本,记为 D v D^v Dv.我们可根据信息熵计算公式计算出 D v D^v Dv的信息嫡,再考虑到不同的分支结点所包含的样本数不同,给分支结点赋予权重 ∣ D v ∣ ∣ D ∣ \frac{|D^v|}{|D|} ∣D∣∣Dv∣,即样本数越多的分支结点的影响越大,于是可计算出用属性 α \alpha α对样本集 D D D进行划分所获得的“信息增益”(information gain)
2.2 信息增益
为了衡量不同划分方式降低信息熵的效果,还需要计算分类后信息熵的减少值(原系统的信息熵与分类后系统的信息熵之差),该减少值称为熵增益或信息增益,其值越大,说明分类后的系统混乱程度越低,即分类越准确。
信息增益的计算公式如下:

一般而言,信息增益越大,则意味着使用属性a来进行划分所获得的“纯度提升”越大。

对于信息增益,举一个西瓜书上面的例子:

2.3 增益率
在上面的介绍中,我们有意忽略了"编号"这一列.若把"编号"也作为一个候选划分属性,可计算出它的信息增益为0.998远大于其他候选划分属性.这很容易理解"编号"将产生 17 个分支,每个分支结点仅包含一个样本,这些分支结点的纯度己达最大.然而,这样的决策树显然不具有泛化能力,无法对新样本进行有效预测.
实际上,信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响,著名的C4.5决策树算法不直接使用信息增益,而是使用“增益率”(gain ratio)来选择最优划分属性.采用信息增益相同的符号表示,增益率定义为

其中,

优点:属性a的可能取值数目越多 (即 V 越大),则 IV(a) 的值通常就越大。
缺点:对取值数目少的属性有偏好
C4.5 算法中使用启发式: 先从候选划分属性中找出信息增益高于平均水平的,再从中选取增益率最高的。
2.4 基尼指数
决策树模型的建树依据主要用到的是基尼系数的概念。反映了从 D 中随机抽取两个样例,其类别标记不一致的概率。
采用基尼系数进行运算的决策树也称为CART决策树。
基尼系数(gini)用于计算一个系统中的失序现象,即系统的混乱程度(纯度)。基尼系数越高,系统的混乱程度就越高(不纯),建立决策树模型的目的就是降低系统的混乱程度(体高纯度),从而得到合适的数据分类效果。
基尼系数的计算公式如下

基尼系数越低表示系统的混乱程度越低(纯度越高),区分度越高,越适合用于分类预测。
在候选属性集合中,选取那个使划分后基尼指数最小的属性。即:

3 剪枝处理
划分选择的各种准则虽然对决策树的尺寸有较大影响,但对泛化性能的影响很有限。是决策树预防“过拟合”的主要手段!
可通过“剪枝”来一定程度避免因决策分支过多,以致于把训练集自身的一些特点当做所有数据都具有的一般性质而导致的过拟合
剪枝方法和程度对决策树泛化性能的影响更为显著(在数据带噪时甚至可能将泛化性能提升 25%)
3.1 预剪枝
从上往下剪枝,通常利用超参数进行剪枝。例如,通过限制树的最大深度(max_depth)便能剪去该最大深度下面的节点。
没有剪枝前:

剪枝后:

3.1.1 预剪枝的优缺点
优点:
- 降低过拟合风险
- 显著减少训练时间和测试时间开销
缺点:
- 欠拟合风险
3.2 后剪枝
从下往上剪枝,大多是根据业务需求剪枝。例如,在违约预测模型中,认为违约概率为45%和50%的两个叶子节点都是高危人群,那么就把这两个叶子节点合并成一个节点。

3.2.1 后剪枝的优缺点
优点:
- 欠拟合风险小
- 泛化性能往往优于预剪枝决策树
缺点:
- 训练时间开销大
4 连续属性处理
根据定义,决策树擅长处理离散属性,但对于连续属性,也是有办法应对的
4.1 连续属性离散化(二分法)
第一步:
假定连续属性 a a a在样本集 D D D上出现 n n n个不同的取值,从小到大排列,记为 a 1 , a 2 , . . . , a n a^1,a^2,...,a^n a1,a2,...,an,基于划分点 t t t,可将 D D D分为子集 D t − D^{-}_{t} Dt−和 D t + D^{+}_{t} Dt+,其中 D t − D^{-}_{t} Dt−包含那些在属性 a a a上取值不大于 t t t的样本, D t + D^{+}_{t} Dt+包含那些在属性 a a a上取值大于 t t t的样本,考虑包含 n − 1 n-1 n−1个元素的候选划分点集合

即把区间 [ a i , a i − 1 ) [a^{i},a^{i-1}) [ai,ai−1)的中位点 a i + a i + 1 2 \frac{a^{i}+a^{i+1}}{2} 2ai+ai+1作为候选划分点
第二步:
采用离散属性值方法,考察这些划分点,选取最优的划分点进行样本集合的划分

其中 G a i n ( D , a , t ) Gain(D,a,t) Gain(D,a,t)是样本集 D D D基于划分点 t t t二分后的信息增益,于是,就可选择使 G a i n ( D , a , t ) Gain(D,a,t) Gain(D,a,t)最大化的划分点

5 多变量决策树
多变量决策树是一种基于树结构进行决策的机器学习方法,可以用于分类和回归任务。它将决策树中的叶子结点转换为一个线性的分类器,用于解决数据集中属性过多的情况。常用的算法有ID3、C4.5、CART和Random Forest。
单变量决策树分类边界:轴平行

单变量和多变量决策树的区别如下图所示:


成熟的决策树软件包
ID3,C4.5,C5.0
J48
相关文章:

【机器学习基础】决策树(Decision Tree)
🚀个人主页:为梦而生~ 关注我一起学习吧! 💡专栏:机器学习 欢迎订阅!后面的内容会越来越有意思~ ⭐特别提醒:针对机器学习,特别开始专栏:机器学习python实战 欢迎订阅&am…...

图神经网络DGL框架,graph classification,多个且不同维度的node feature 训练
node feature 维度不同 我现在有许多不同的图要加入训练,每个图的节点特征维度不同,第一张图n_weight特征有10条数据,第二张图n_weight特征有15条数据,但是训练的时候,需要维度都对其,所以直接做0 padding…...
2022国赛真题:用什么来做计算 A)
蓝桥杯(Web大学组)2022国赛真题:用什么来做计算 A
判分标准 实现重置(AC)功能,得 1 分。 实现计算式子和结果显示功能,得 3 分。 实现计算功能,得 6 分。 应该按要求来就行吧,,一开始还在想是否要考虑小数点个数的问题还有式子是否有效…… 笔记…...

Linux POSIX信号量 线程池
Linux POSIX信号量 线程池 一. 什么是POSIX信号量?二. POSIX信号量实现原理三. POSIX信号量接口函数四. 基于环形队列的生产消费模型五. 线程池 一. 什么是POSIX信号量? POSIX信号量是一种用于同步和互斥操作的机制,属于POSIX(Po…...
Sentinel(理论版)
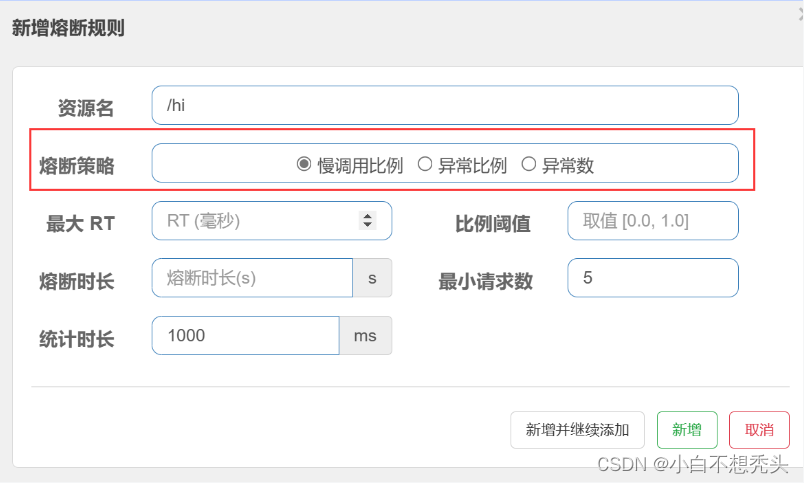
Sentinel 1.什么是Sentinel Sentinel 是一个开源的流量控制组件,它主要用于在分布式系统中实现稳定性与可靠性,如流量控制、熔断降级、系统负载保护等功能。简单来说,Sentinel 就像是一个交通警察,它可以根据系统的实时流量&…...
python3 获取某个文件夹所有的pdf文件表格提取表格并一起合并到excel文件
下面是一个完整的示例,其中包括了merge_tables_to_excel函数的定义,并且假设该函数的功能是从每个PDF文件中提取第一个表格并将其合并到一个Excel文件中: import os from pathlib import Path import pandas as pd import pdfplumber …...

【AIGC】Stable Diffusion的模型入门
下载好相关模型文件后,直接放入Stable Diffusion相关目录即可使用,Stable Diffusion 模型就是我们日常所说的大模型,下载后放入**\webui\models\Stable-diffusion**目录,界面上就会展示相应的模型选项,如下图所示。作者…...
【JavaEE】_HTTP请求首行详情
目录 1. URL 2. 方法 2.1 GET方法 2.2 POST方法 2.3 GET与POST的区别 2.4 低频使用方法 1. URL 在mysql JDBC中已经提到过URL的相关概念: 如需查看有关JDBC更多内容,原文链接如下: 【MySQL】_JDBC编程-CSDN博客 URL用于描述某个资源…...
Linux第48步_编译正点原子的出厂Linux内核源码
编译正点原子的出厂 Linux 内核源码,为后面移植linux做准备。研究对象如下: 1)、linux内核镜像文件“uImage” 路径为“arch/arm/boot”; 2)、设备树文件“stm32mp157d-atk.dtb” 路径为“arch/arm/boot/dts” 3)、默认配置文件“stm32m…...
程序员为什么不喜欢关电脑?
程序员为什么不喜欢关电脑? 本人40 最近待业。,希望 3月前能再就业吧!就不喜欢关电脑 这个问题来说是不好习惯。毕竟你的电脑不是服务器,哈哈。但是程序员都很懒,能自动化的,就让机器干。我在此之前 也工作…...
【初始RabbitMQ】了解和安装RabbitMQ
RabbitMQ的概念 RabbitMQ是一个消息中间件:他可以接受并转发消息。例如你可以把它当做一个快递站点,当你要发送一个包 裹时,你把你的包裹放到快递站,快递员最终会把你的快递送到收件人那里,按照这种逻辑 RabbitMQ 是 …...
Linux第56步_根文件系统第3步_将busybox构建的根文件系统烧录到EMMC
1、第1次将“rootfs”打包 1)、打开第1个终端,准备在“mnt”目录下创建挂载目录“rootfs”; 输入“ls回车” 输入“cd /mnt回车” 输入“ls回车”,查看“mnt”目录下的文件和文件夹 输入“sudo mkdir rootfs回车”,在“mnt”…...
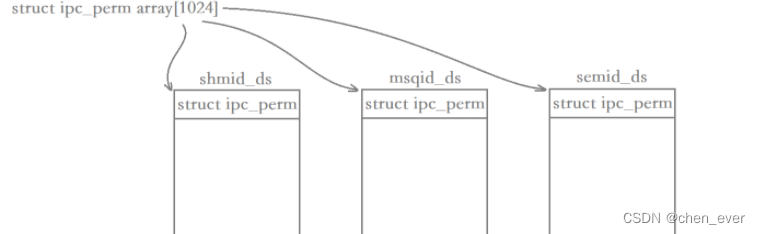
Linux进程间通信(三)-----System V消息队列
消息队列的概念及原理 消息队列实际上就是在系统当中创建了一个队列,队列当中的每个成员都是一个数据块,这些数据块都由类型和信息两部分构成,两个互相通信的进程通过某种方式看到同一个消息队列,这两个进程向对方发数据时&#x…...

Elasticsearch:混合搜索是 GenAI 应用的未来
在这个竞争激烈的人工智能时代,自动化和数据为王。 从庞大的存储库中有效地自动化搜索和检索信息的过程的能力变得至关重要。 随着技术的进步,信息检索方法也在不断进步,从而导致了各种搜索机制的发展。 随着生成式人工智能模型成为吸引力的中…...

态、势、感、知的偏序、全序与无序
在态势感知中,"态"、"势"、"感"和"知"可以被理解为描述不同层次的概念。而在偏序、全序和无序方面,它们可以有不同的关系,简单地说,偏序关系表示部分的可比较性,全序关系表示…...

【从Python基础到深度学习】 8. VIM两种状态
一、安装 sudo apt install vim 二、VIM两种模式 - 命令状态/编辑状态 1.1 进入/退出VIM 进入VIM vim 退出vim :q <enter> 2.2 根目录下添加配置文件 window下创建vimrc类型文件内容如下: set nu set cursorline set hlsearch set tabstop4 使用Wins…...
java微服务面试篇
目录 目录 SpringCloud Spring Cloud 的5大组件 服务注册 Eureka Nacos Eureka和Nacos的对比 负载均衡 负载均衡流程 Ribbon负载均衡策略 自定义负载均衡策略 熔断、降级 服务雪崩 服务降级 服务熔断 服务监控 为什么需要监控 服务监控的组件 skywalking 业务…...

OpenAI 生成视频模型 Sora 论文翻译
系列文章目录 前言 视频生成模型作为世界模拟器 本技术报告的重点是 (1) 将所有类型的视觉数据转换为统一表示,以便对生成模型进行大规模训练的方法,以及 (2) 对索拉的能力和局限性的定性评估。 该报告不包括模型和实现细节。 许多先前的工作使用各种方…...

2.13日学习打卡----初学RocketMQ(四)
2.13日学习打卡 目录: 2.13日学习打卡一.RocketMQ之Java ClassDefaultMQProducer类DefaultMQPushConsumer类Message类MessageExt类 二.RocketMQ 消费幂消费过程幂等消费速度慢的处理方式 三.RocketMQ 集群服务集群特点单master模式多master模式多master多Slave模式-…...
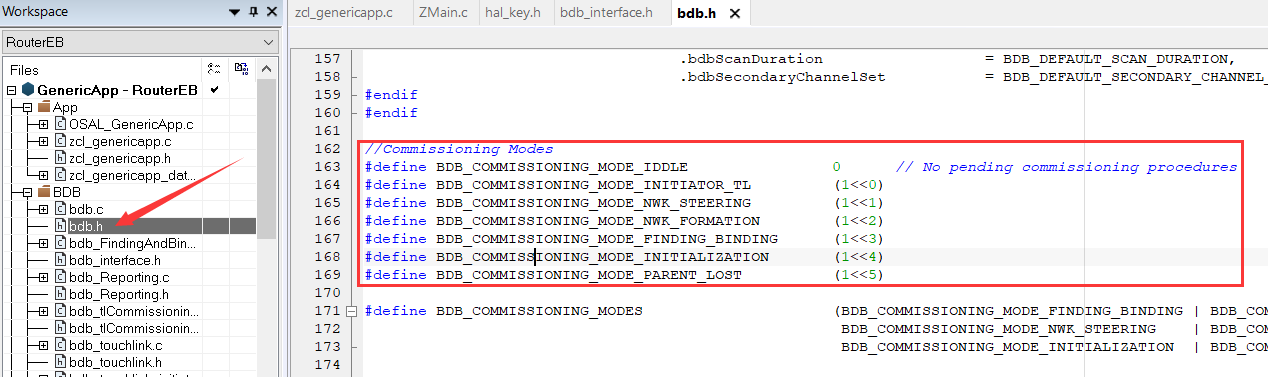
ZigBee学习——BDB
✨本博客参考了善学坊的教程,并总结了在实现过程中遇到的问题。 善学坊官网 文章目录 一、BDB简介二、BDB Commissioning Modes2.1 Network Steering2.2 Network Formation2.3 Finding and Binding(F & B)2.4 Touchlink 三、BDB Commissi…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
