【记录】个人博客或笔记中的数学符号设定
note
- 这里记录个人博客中常用的数学符号数学格式和对应含义
文章目录
- note
- 数与数组
- 索引
- 集合
- 线性代数
- 微积分
- 概率和信息论
- 数据与概率分布
- 函数
- 深度学习中的常用数学表达方式
数与数组
α 标量 α 向量 A 矩阵 A 张量 I n n 行 n 列单位矩阵 v w 单词 w 的分布式向量表示 e w 单词 w 的独热向量表示: [ 0 , 0 , … , 1 , 0 , … 0 ] , w 下标处元素为 1 \begin{array}{ll} \boldsymbol{\alpha} & \text { 标量 } \\ \boldsymbol{\alpha} & \text { 向量 } \\ \boldsymbol{A} & \text { 矩阵 } \\ \mathbf{A} & \text { 张量 } \\ \boldsymbol{I}_n & n \text { 行 } n \text { 列单位矩阵 } \\ \boldsymbol{v}_w & \text { 单词 } w \text { 的分布式向量表示 } \\ \boldsymbol{e}_w & \text { 单词 } w \text { 的独热向量表示: }[0,0, \ldots, 1,0, \ldots 0], w \text { 下标处元素为 } 1 \end{array} ααAAInvwew 标量 向量 矩阵 张量 n 行 n 列单位矩阵 单词 w 的分布式向量表示 单词 w 的独热向量表示: [0,0,…,1,0,…0],w 下标处元素为 1
索引
α i 向量 α 中索引 i 处的元素 α − i 向量 α 中除索引 i 之外的元素 w i : j 序列 w 中从第 i 个元素到第 j 个元素组成的片段或子序列 A i j 矩阵 A 中第 i 行、第 j 列处的元素 A i : 矩阵 A 中第 i 行 A : j 矩阵 A 中第 j 列 A i j k 三维张量 A 中索引为 ( i , j , k ) 处元素 A : : i 三维张量 A 中的一个二维切片 \begin{array}{ll} \alpha_i & \text { 向量 } \boldsymbol{\alpha} \text { 中索引 } i \text { 处的元素 } \\ \alpha_{-i} & \text { 向量 } \boldsymbol{\alpha} \text { 中除索引 } i \text { 之外的元素 } \\ w_{i: j} & \text { 序列 } w \text { 中从第 } i \text { 个元素到第 } j \text { 个元素组成的片段或子序列 } \\ A_{i j} & \text { 矩阵 } \boldsymbol{A} \text { 中第 } i \text { 行、第 } j \text { 列处的元素 } \\ \boldsymbol{A}_{i:} & \text { 矩阵 } \boldsymbol{A} \text { 中第 } i \text { 行 } \\ \boldsymbol{A}_{: j} & \text { 矩阵 } \boldsymbol{A} \text { 中第 } j \text { 列 } \\ A_{i j k} & \text { 三维张量 } \mathbf{A} \text { 中索引为 }(i, j, k) \text { 处元素 } \\ \mathbf{A}_{:: i} & \text { 三维张量 } \mathbf{A} \text { 中的一个二维切片 } \end{array} αiα−iwi:jAijAi:A:jAijkA::i 向量 α 中索引 i 处的元素 向量 α 中除索引 i 之外的元素 序列 w 中从第 i 个元素到第 j 个元素组成的片段或子序列 矩阵 A 中第 i 行、第 j 列处的元素 矩阵 A 中第 i 行 矩阵 A 中第 j 列 三维张量 A 中索引为 (i,j,k) 处元素 三维张量 A 中的一个二维切片
集合
A 集合 R 实数集 C 复数集 { 0 , 1 , … , n } 含 0 和 n 的正整数的集合 [ a , b ] a 到 b 的实数闭区间 ( a , b ] a 到 b 的实数左开右闭区间 \begin{array}{ll} \mathbb{A} & \text { 集合 } \\ \mathbb{R} & \text { 实数集 } \\ \mathbb{C} & \text { 复数集 } \\ \{0,1, \ldots, n\} & \text { 含 } 0 \text { 和 } n \text { 的正整数的集合 } \\ {[a, b]} & a \text { 到 } b \text { 的实数闭区间 } \\ (a, b] & a \text { 到 } b \text { 的实数左开右闭区间 } \end{array} ARC{0,1,…,n}[a,b](a,b] 集合 实数集 复数集 含 0 和 n 的正整数的集合 a 到 b 的实数闭区间 a 到 b 的实数左开右闭区间
线性代数
A ⊤ 矩阵 A 的转置 A ⊙ B 矩阵 A 与矩阵 B 的 Hadamard 乘积 det ( A ) 矩阵 A 的行列式 [ x ; y ] 向量 x 与 y 的拼接 [ U ; V ] 矩阵 A 与 V 沿行向量拼接 x ⋅ y 或 x ⊤ y 向量 x 与 y 的点积 \begin{array}{ll} \boldsymbol{A}^{\top} & \text { 矩阵 } \boldsymbol{A} \text { 的转置 } \\ \boldsymbol{A} \odot \boldsymbol{B} & \text { 矩阵 } \boldsymbol{A} \text { 与矩阵 } \boldsymbol{B} \text { 的 Hadamard 乘积 } \\ \operatorname{det}(\boldsymbol{A}) & \text { 矩阵 } \boldsymbol{A} \text { 的行列式 } \\ {[\boldsymbol{x} ; \boldsymbol{y}]} & \text { 向量 } \boldsymbol{x} \text { 与 } \boldsymbol{y} \text { 的拼接 } \\ {[\boldsymbol{U} ; \boldsymbol{V}]} & \text { 矩阵 } \boldsymbol{A} \text { 与 } \boldsymbol{V} \text { 沿行向量拼接 } \\ \boldsymbol{x} \cdot \boldsymbol{y} \text { 或 } \boldsymbol{x}^{\top} \boldsymbol{y} & \text { 向量 } \boldsymbol{x} \text { 与 } \boldsymbol{y} \text { 的点积 } \end{array} A⊤A⊙Bdet(A)[x;y][U;V]x⋅y 或 x⊤y 矩阵 A 的转置 矩阵 A 与矩阵 B 的 Hadamard 乘积 矩阵 A 的行列式 向量 x 与 y 的拼接 矩阵 A 与 V 沿行向量拼接 向量 x 与 y 的点积
微积分
d y d x y 对 x 的导数 ∂ y ∂ x y 对 x 的偏导数 ∇ x y y 对向量 x 的梯度 ∇ x y y 对矩阵 X 的梯度 ∇ x y y 对张量 X 的梯度 \begin{array}{ll} \frac{\mathrm{d} y}{\mathrm{~d} x} & y \text { 对 } x \text { 的导数 } \\ \frac{\partial y}{\partial x} & y \text { 对 } x \text { 的偏导数 } \\ \nabla \boldsymbol{x} y & y \text { 对向量 } \boldsymbol{x} \text { 的梯度 } \\ \nabla \boldsymbol{x} y & y \text { 对矩阵 } \boldsymbol{X} \text { 的梯度 } \\ \nabla \mathbf{x} y & y \text { 对张量 } \mathbf{X} \text { 的梯度 } \end{array} dxdy∂x∂y∇xy∇xy∇xyy 对 x 的导数 y 对 x 的偏导数 y 对向量 x 的梯度 y 对矩阵 X 的梯度 y 对张量 X 的梯度
概率和信息论
a ⊥ b 随机变量 a 与 b 独立 a ⊥ b ∣ c 随机变量 a 与 b 关于 c 条件独立 P ( a ) 离散变量概率分布 p ( a ) 连续变量概率分布 a ∼ P 随机变量 a 服从分布 P E x ∼ P ( f ( x ) ) 或 f ( x ) 在分布 P ( x ) 下的期望 E ( f ( x ) ) Var ( f ( x ) ) f ( x ) 在分布 P ( x ) 下的方差 Cov ( f ( x ) , g ( x ) ) f ( x ) 与 g ( x ) 在分布 P ( x ) 下的协方差 H ( f ( x ) ) 随机变量 x 的信息熵 D K L ( P ∥ Q ) 概率分布 P 与 Q 的 K L 散度 N ( μ , Σ ) 均值为 μ 、协方差为 Σ 的高斯分布 \begin{array}{ll} a \perp b & \text { 随机变量 } a \text { 与 } b \text { 独立 } \\ a \perp b \mid c & \text { 随机变量 } a \text { 与 } b \text { 关于 } c \text { 条件独立 } \\ P(a) & \text { 离散变量概率分布 } \\ p(a) & \text { 连续变量概率分布 } \\ a \sim P & \text { 随机变量 } a \text { 服从分布 } P \\ \mathbb{E}_{x \sim P}(f(x)) \text { 或 } & f(x) \text { 在分布 } P(x) \text { 下的期望 } \\ \mathbb{E}(f(x)) & \\ \operatorname{Var}(f(x)) & f(x) \text { 在分布 } P(x) \text { 下的方差 } \\ \operatorname{Cov}(f(x), g(x)) & f(x) \text { 与 } g(x) \text { 在分布 } P(x) \text { 下的协方差 } \\ H(f(x)) & \text { 随机变量 } x \text { 的信息熵 } \\ D_{K L}(P \| Q) & \text { 概率分布 } P \text { 与 } Q \text { 的 } \mathrm{KL} \text { 散度 } \\ \mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma}) & \text { 均值为 } \boldsymbol{\mu} \text { 、协方差为 } \boldsymbol{\Sigma} \text { 的高斯分布 } \end{array} a⊥ba⊥b∣cP(a)p(a)a∼PEx∼P(f(x)) 或 E(f(x))Var(f(x))Cov(f(x),g(x))H(f(x))DKL(P∥Q)N(μ,Σ) 随机变量 a 与 b 独立 随机变量 a 与 b 关于 c 条件独立 离散变量概率分布 连续变量概率分布 随机变量 a 服从分布 Pf(x) 在分布 P(x) 下的期望 f(x) 在分布 P(x) 下的方差 f(x) 与 g(x) 在分布 P(x) 下的协方差 随机变量 x 的信息熵 概率分布 P 与 Q 的 KL 散度 均值为 μ 、协方差为 Σ 的高斯分布
数据与概率分布
X 或 D 数据集 x ( i ) 数据集中第 i 个样本(输入) y ( i ) 或 y ( i ) 第 i 个样本 x ( i ) 的标签(输出) \begin{array}{ll} \mathbb{X} \text { 或 } \mathbb{D} & \text { 数据集 } \\ \boldsymbol{x}^{(i)} & \text { 数据集中第 } i \text { 个样本(输入) } \\ \boldsymbol{y}^{(i)} \text { 或 } y^{(i)} & \text { 第 } i \text { 个样本 } \boldsymbol{x}^{(i)} \text { 的标签(输出) } \end{array} X 或 Dx(i)y(i) 或 y(i) 数据集 数据集中第 i 个样本(输入) 第 i 个样本 x(i) 的标签(输出)
函数
f : A ⟶ B 由定义域 A 到值域 B 的函数(映射) f f ∘ g f 与 g 的复合函数 f ( x ; θ ) 由参数 θ 定义的关于 x 的函数(也可以直接写作 f ( x ) , 省略 θ ) log x x 的自然对数函数 σ ( x ) Sigmoid 函数 1 1 + exp ( − x ) ∥ x ∥ p x 的 L p 范数 ∥ x ∥ x 的 L 2 范数 1 condition 条件指示函数:如果 condition 为真, 则值为 1 ; 否则值为 0 \begin{array}{ll} f: \mathcal{A} \longrightarrow \mathcal{B} & \text { 由定义域 } \mathcal{A} \text { 到值域 } \mathcal{B} \text { 的函数(映射) } f \\ f \circ g & f \text { 与 } g \text { 的复合函数 } \\ f(\boldsymbol{x} ; \boldsymbol{\theta}) & \text { 由参数 } \boldsymbol{\theta} \text { 定义的关于 } \boldsymbol{x} \text { 的函数(也可以直接写作 } f(\boldsymbol{x}), \text { 省略 } \boldsymbol{\theta}) \\ \log x & x \text { 的自然对数函数 } \\ \sigma(x) & \text { Sigmoid 函数 } \frac{1}{1+\exp (-x)} \\ \|\boldsymbol{x}\|_p & \boldsymbol{x} \text { 的 } L^p \text { 范数 } \\ \|\boldsymbol{x}\| & \boldsymbol{x} \text { 的 } L^2 \text { 范数 } \\ \mathbf{1}^{\text {condition }} & \text { 条件指示函数:如果 condition 为真, 则值为 } 1 \text {; 否则值为 } 0 \end{array} f:A⟶Bf∘gf(x;θ)logxσ(x)∥x∥p∥x∥1condition 由定义域 A 到值域 B 的函数(映射) ff 与 g 的复合函数 由参数 θ 定义的关于 x 的函数(也可以直接写作 f(x), 省略 θ)x 的自然对数函数 Sigmoid 函数 1+exp(−x)1x 的 Lp 范数 x 的 L2 范数 条件指示函数:如果 condition 为真, 则值为 1; 否则值为 0
深度学习中的常用数学表达方式
- 给定词表 V \mathbb{V} V, 其大小为 ∣ V ∣ |\mathbb{V}| ∣V∣
- 序列 x = x 1 , x 2 , … , x n x=x_1, x_2, \ldots, x_n x=x1,x2,…,xn 中第 i i i 个单词 x i x_i xi 的词向量 v x i \boldsymbol{v}_{x_i} vxi
- 损失函数 L \mathcal{L} L 为负对数似然函数: L ( θ ) = − ∑ ( x , y ) log P ( y ∣ x 1 … x n ) \mathcal{L}(\boldsymbol{\theta})=-\sum_{(x, y)} \log P\left(y \mid x_1 \ldots x_n\right) L(θ)=−∑(x,y)logP(y∣x1…xn)
- 算法的空间复杂度为 O ( m n ) \mathcal{O}(m n) O(mn)
相关文章:

【记录】个人博客或笔记中的数学符号设定
note 这里记录个人博客中常用的数学符号数学格式和对应含义 文章目录 note数与数组索引集合线性代数微积分概率和信息论数据与概率分布函数深度学习中的常用数学表达方式 数与数组 α 标量 α 向量 A 矩阵 A 张量 I n n 行 n 列单位矩阵 v w 单词 w 的分布式向量表示 …...

Redis Sentinel工作原理
Redis Sentinel是Redis的高可用性解决方案。它主要用来监控Redis master和slave服务器的运行状态,并在master宕机时自动进行故障转移,即从slave节点中选举出新的master节点,并让其余的slave节点指向新的master节点。 Redis Sentinel工作原理…...

GEE入门篇|遥感专业术语:理论介绍
本章的目的是介绍遥感图像的一些主要特征,以及如何在Earth Engine中检查它们。我们将讨论空间分辨率、时间分辨率和光谱分辨率,以及如何访问重要的图像元数据。将了解到来自不同卫星平台上的几个传感器的图像数据。在本章的学习完成后,您将能…...

react中如何做到中断diff过程和恢复
workLoop是 实现时间切片 和 可中断渲染的核心,简要说明如下: // 并发任务的入口function workLoopConcurrent() {// Perform work until Scheduler asks us to yield// 有任务 & 是否需要中断while (workInProgress ! null && !shouldYiel…...

python:PyPDF2 从PDF文件中提取目录
我发现 pypdf 和 pypdf2 的作者是同一人:Mathieu Fenniak pip install pypdf2 ; pypdf2-3.0.1-py3-none-any.whl (232 kB) 编写 pdf_read_dir.py 如下 # -*- coding: utf-8 -*- """ pypdf23.0.1 从PDF中提取目录 """ import os…...

Java 2:运算符、表达式和语句
2.1 运算符与表达式 Java提供了丰富的运算符,如算术运算符、关系运算符、逻辑运算符、位运算符等。Java语言中的绝大多数运算符和C语言相同,基本语句如条件分支语句,循环语句等,也和C语言类似。 2.1.1算术运算符与算术表达式 1…...

批量提取word文件中文本框内容的三种方法
一、问题的提出 在日常的办公中,有时需要提取多个word文件中的文字框的内容。有时,文字框的数量比较多,而且处于文档的不同位置,手工提取比较耗时耗力,同时也可能会产生遗漏。 我们也可以通过VBA和Python来解决这个问…...
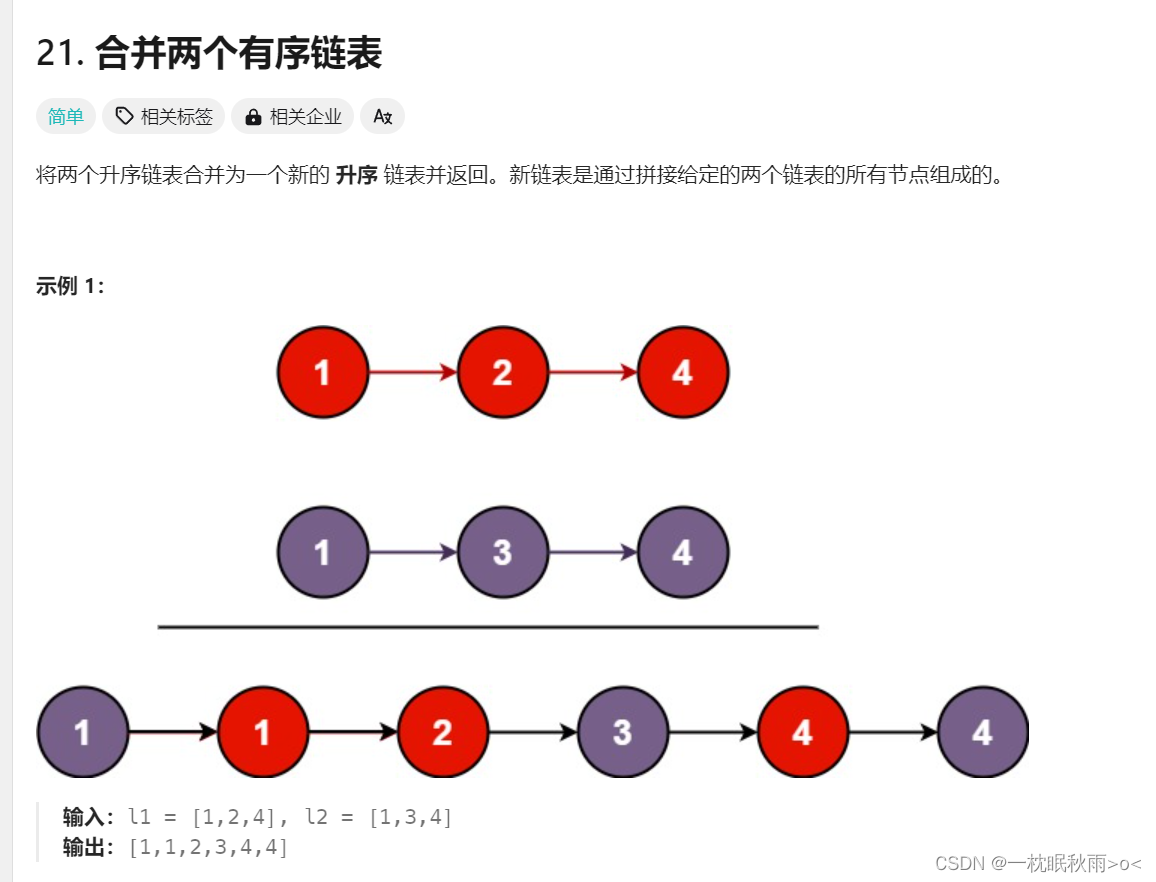
Leecode之合并两个有序链表
一.题目及剖析 https://leetcode.cn/problems/merge-two-sorted-lists/description/ 二.思路引入 用指针遍历两个链表并实时比较,较小的元素进行尾插,然后较小元素的指针接着向后遍历 三.代码引入 /*** Definition for singly-linked list.* struct ListNode {* int va…...

陶建国教授谈中西方文化的差异与交融
龙年到来,这个春节里,“龙”字的英文翻译引发关注,冲上了热搜,网友发现,“龙”不再翻译为“dragon”,而是龙字的谐音“loong”。原来,在西方人的眼里,龙是凶猛的怪兽,具有…...

Ps:画笔选项
画笔选项 Brush Options提供了对画笔(圆形笔刷)基本属性的控制,比如大小、硬度、间距、角度和圆度等。 Photoshop 中的快速选择工具、污点修复画笔工具、修复画笔工具、颜色替换工具、背景橡皮擦工具等的工具选项栏上提供了这种圆形笔刷选项。…...
嵌入式——Flash(W25Q64)
目录 一、初识W25Q64 1. 基本认识 2. 引脚介绍 编辑 二、W25Q64特性 1. SPI模式 2. 双输出SPI方式 三、状态寄存器 1. BUSY位 2. WEL位 3. BP2、BP1、 BP0位 4. TB位 5. 保留位 6. SRP位 四、常用操作指令 1. 写使能指令(06h) 2. 写禁…...

stm32:pwm output模块,记录一下我是用smt32,输出pwm波的记录--(实现--重要)
我是实现了输出pwm波,频率固定,占空比可以不断调整的方法,将PA0接到示波器上,可以看到是一个标准的PWM波,如图下面示波器图。 1,首先是ioc的配置 我刚开始设置的分频的倍数是7199,使得分频的太大了,示波器显示不了,最后修改为71就可以,我之前设置读取pwm也是一样的…...
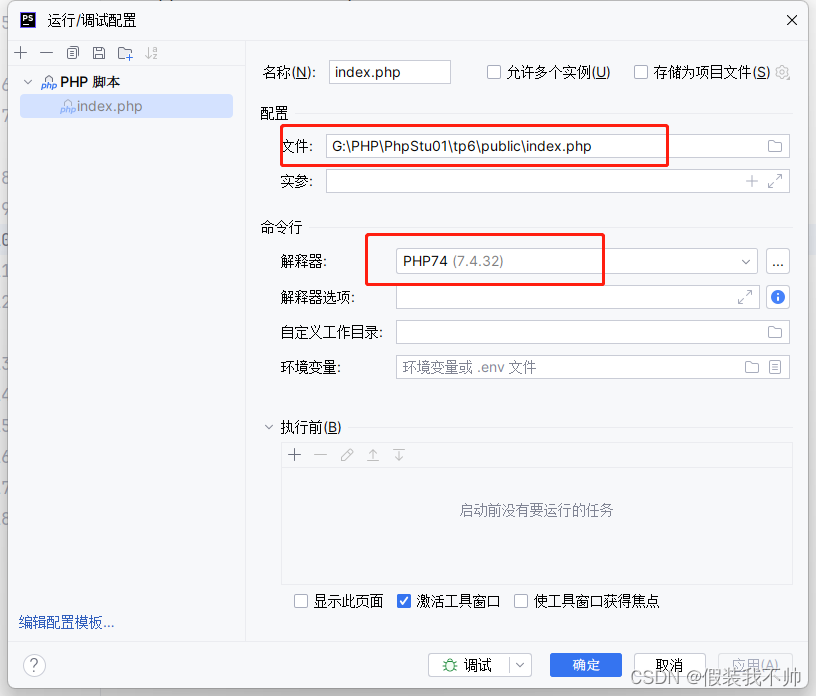
phpstrom创建thinkphp项目
安装php和composer 参考 安装phpstrom 创建项目 查看thinkphp版本 https://packagist.org/packages/topthink/think 打开所在项目编辑配置 即可调试运行...

【Linux】线程同步
线程同步 一、条件变量1. 同步概念2. 条件变量概念3. 条件变量接口(1)pthread_cond_init()(2)pthread_cond_destroy()(3)pthread_cond_wait()(4)pthread_cond_signal()(5…...

如何在多头自注意力机制的交叉学习中引入对于物理、生理、心理世界客观规律的对照验证...
要在多头自注意力机制的交叉学习中引入对于物理世界客观规律的对照验证,可以考虑以下方法: 1、引入物理模型 首先,建立一个物理模型,该模型能够描述物理世界中的客观规律。这个模型可以是已知的科学理论,也可以是通过实…...

智慧公厕:让智慧城市的公共厕所焕发“智慧活力”
智慧城市的建设已经进入了一个新的阶段,不仅仅是智慧交通、智慧环保,如今甚至连公厕都开始迎来智慧化时代。智慧公厕作为智慧城市的神经末梢,正在通过信息化、数字化和智慧化的方式,实现全方位的精细化管理。本文以智慧公厕源头专…...

vue导出word文档(图文示例)
第076个 查看专栏目录: VUE 本文章目录 示例说明示例效果图导出的文件效果截图示例源代码参数说明:重要提示:API 参考网址 示例说明 在Vue中导出Word文档,可以使用第三方库file-saver和html-docx-js。首先需要安装这两个库: npm …...

【C Primer Plus第六版 学习笔记】 第十七章 高级数据表示
有基础,进阶用,个人查漏补缺 链表:假设要编写一个程序,让用户输入一年内看过的所有电影,要储存每部影片的片名和评级。 #include <stdio.h> #include <stdlib.h> /* 提供malloc()的原型 */ #include <s…...
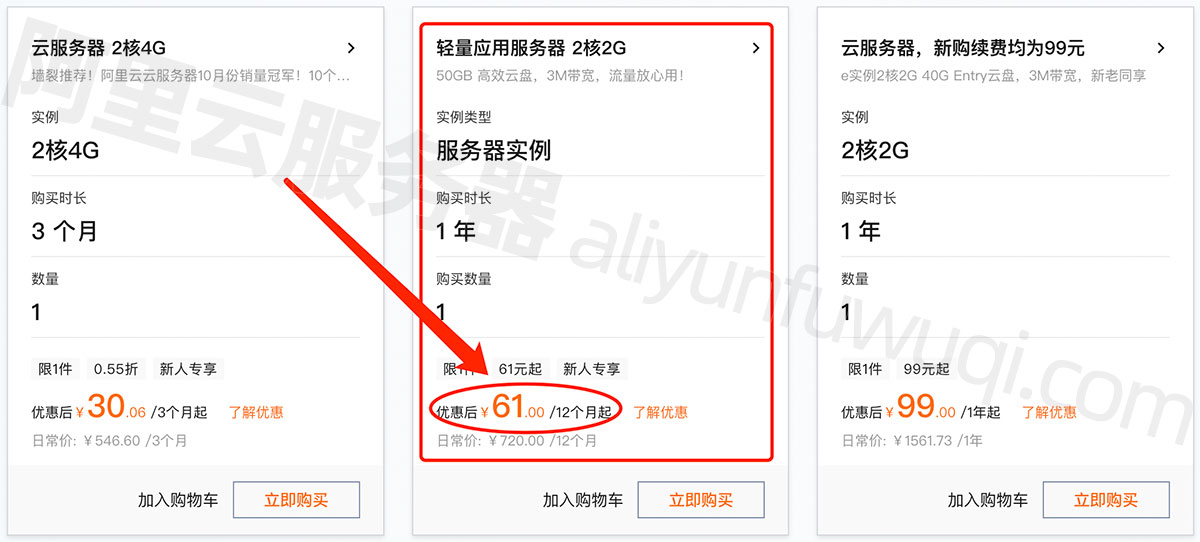
租用一个服务器需要多少钱?2024阿里云新版报价
2024年最新阿里云服务器租用费用优惠价格表,轻量2核2G3M带宽轻量服务器一年61元,折合5元1个月,新老用户同享99元一年服务器,2核4G5M服务器ECS优惠价199元一年,2核4G4M轻量服务器165元一年,2核4G服务器30元3…...

python-产品篇-游戏-成语填填乐
文章目录 准备代码效果 准备 无需其他文件,复制即用 代码 import random list["春暖花开","十字路口","千军万马","白手起家","张灯结彩","风和日丽","万里长城","人来人往",&…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...
