DAY53:动态规划(买股票的最佳时机)
Leetcode: 121 买卖股票的最佳时机
代码随想录
1、确定下标和含义
dp[i][0]表示当天持有股票所得的最多现金
do[i][1]表示当天不持有股票的最多现金
2、递推公式
(1)如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
- 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
- 第i天买入股票,所得现金就是买入今天的股票后所得现金即:-prices[i]
那么dp[i][0]应该选所得现金最大的,所以dp[i][0] = max(dp[i - 1][0], -prices[i]);
(2)如果第i天不持有股票即dp[i][1], 也可以由两个状态推出来
- 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
第i天卖出股票,所得现金就是按照今天股票价格卖出后所得现金即:prices[i] + dp[i - 1][0]
同样dp[i][1]取最大的,dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
3、初始化
dp[0][0]表示第0天持有股票,此时的持有股票就一定是买入股票了,所以dp[0][0] -= prices[0];
dp[0][1]表示第0天不持有股票,不持有股票那么现金就是0,所以dp[0][1] = 0;
时间复杂度:O(n)
空间复杂度:O(n)
class Solution {
public:int maxProfit(vector<int>& prices) {int len = prices.size();if(len == 0) return 0;vector<vector<int>> dp(len, vector<int>(2));dp[0][0] -= prices[0];dp[0][1] = 0;for(int i = 1; i < len; i++){dp[i][0] = max(dp[i - 1][0], -prices[i]);dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);}return dp[len - 1][1];//最后肯定卖出}
};Leetcode: 122 买卖股票的最佳时机II
与上题不同的是,这道题可以反复卖出股票。
所以就体现在状态公式上
如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
- 第i-1天就持有股票,那么所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
- 第i天买入股票,所得现金就是昨天不持有股票的所得现金减去今天的股票价格 即:dp[i - 1][1] - prices[i]
(2)如果第i天不持有股票即dp[i][1]的情况, 依然可以由两个状态推出来
- 第i-1天就不持有股票,那么所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
- 第i天卖出股票,所得现金就是按照今天股票价格卖出后所得现金即:prices[i] + dp[i - 1][0]
时间复杂度:O(n)
空间复杂度:O(n)
class Solution {
public:int maxProfit(vector<int>& prices) {int len = prices.size();vector<vector<int>> dp(len, vector<int>(2, 0));dp[0][0] -= prices[0];dp[0][1] = 0;for (int i = 1; i < len; i++) {dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); // 注意这里是和121. 买卖股票的最佳时机唯一不同的地方。dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);}return dp[len - 1][1];}
};之前我们用贪心的方法做过这道题,所以可以回顾一下。
相关文章:
)
DAY53:动态规划(买股票的最佳时机)
Leetcode: 121 买卖股票的最佳时机 代码随想录 1、确定下标和含义 dp[i][0]表示当天持有股票所得的最多现金 do[i][1]表示当天不持有股票的最多现金 2、递推公式 (1)如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来 第i-1天就…...

快速实现用户认证:使用Python和Flask配合PyJWT生成与解密Token的教程及示例代码
生成token 与解密 token 和 拦截器 #学习交流 访问 # https://v.iiar.cnimport jwt import datetime from models import XUser from flask import request, jsonify from functools import wrapsSECRET_KEY XPay# 创建token def generate_token(user_id):try:payload {exp:…...

外汇110:外汇做空是什么意思?如何运作?一文读懂
外汇市场允许卖空,就像众多金融市场一样。但什么是卖空呢?如何外汇做空?在本文中,我们将讨论如何做空货币。什么是外汇做空? 外汇做空(Short Selling)是外汇市场上的一种投资方式。它指的是投资…...

【记录】个人博客或笔记中的数学符号设定
note 这里记录个人博客中常用的数学符号数学格式和对应含义 文章目录 note数与数组索引集合线性代数微积分概率和信息论数据与概率分布函数深度学习中的常用数学表达方式 数与数组 α 标量 α 向量 A 矩阵 A 张量 I n n 行 n 列单位矩阵 v w 单词 w 的分布式向量表示 …...

Redis Sentinel工作原理
Redis Sentinel是Redis的高可用性解决方案。它主要用来监控Redis master和slave服务器的运行状态,并在master宕机时自动进行故障转移,即从slave节点中选举出新的master节点,并让其余的slave节点指向新的master节点。 Redis Sentinel工作原理…...

GEE入门篇|遥感专业术语:理论介绍
本章的目的是介绍遥感图像的一些主要特征,以及如何在Earth Engine中检查它们。我们将讨论空间分辨率、时间分辨率和光谱分辨率,以及如何访问重要的图像元数据。将了解到来自不同卫星平台上的几个传感器的图像数据。在本章的学习完成后,您将能…...

react中如何做到中断diff过程和恢复
workLoop是 实现时间切片 和 可中断渲染的核心,简要说明如下: // 并发任务的入口function workLoopConcurrent() {// Perform work until Scheduler asks us to yield// 有任务 & 是否需要中断while (workInProgress ! null && !shouldYiel…...

python:PyPDF2 从PDF文件中提取目录
我发现 pypdf 和 pypdf2 的作者是同一人:Mathieu Fenniak pip install pypdf2 ; pypdf2-3.0.1-py3-none-any.whl (232 kB) 编写 pdf_read_dir.py 如下 # -*- coding: utf-8 -*- """ pypdf23.0.1 从PDF中提取目录 """ import os…...

Java 2:运算符、表达式和语句
2.1 运算符与表达式 Java提供了丰富的运算符,如算术运算符、关系运算符、逻辑运算符、位运算符等。Java语言中的绝大多数运算符和C语言相同,基本语句如条件分支语句,循环语句等,也和C语言类似。 2.1.1算术运算符与算术表达式 1…...

批量提取word文件中文本框内容的三种方法
一、问题的提出 在日常的办公中,有时需要提取多个word文件中的文字框的内容。有时,文字框的数量比较多,而且处于文档的不同位置,手工提取比较耗时耗力,同时也可能会产生遗漏。 我们也可以通过VBA和Python来解决这个问…...
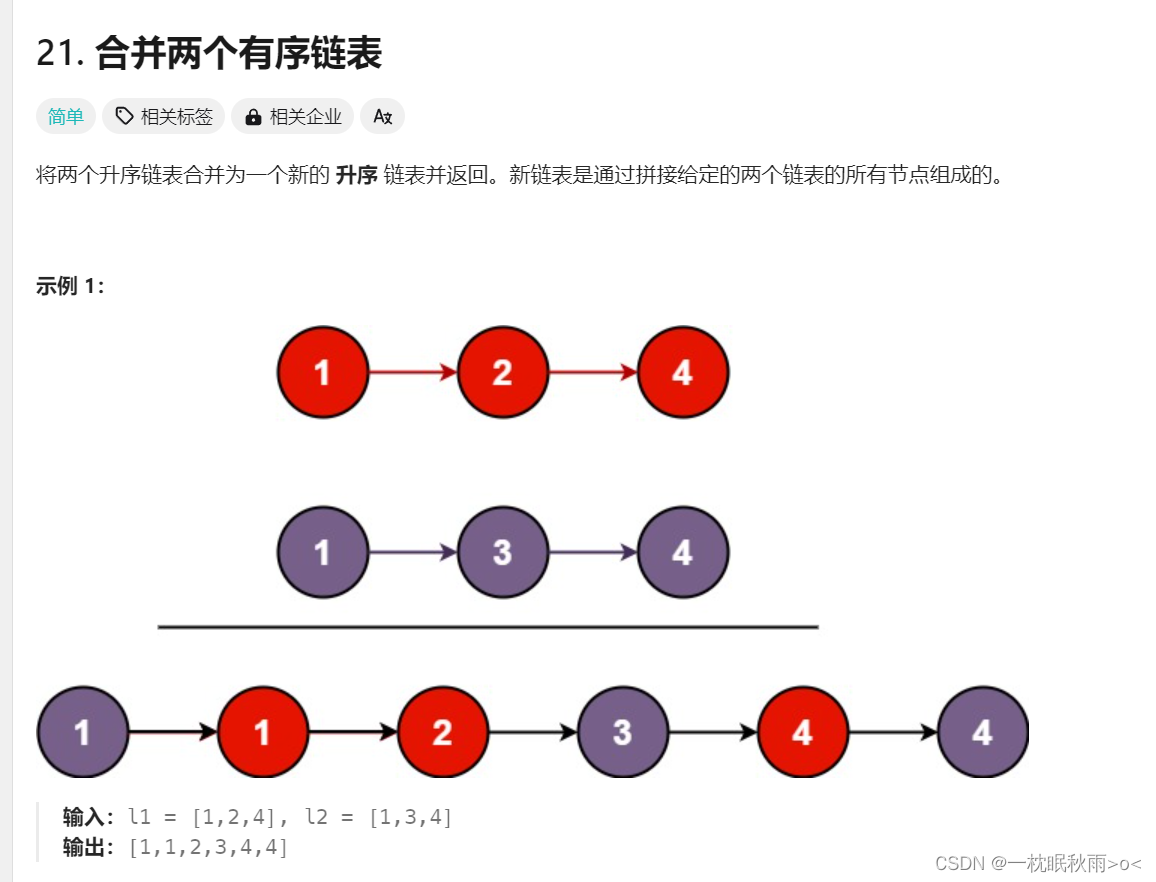
Leecode之合并两个有序链表
一.题目及剖析 https://leetcode.cn/problems/merge-two-sorted-lists/description/ 二.思路引入 用指针遍历两个链表并实时比较,较小的元素进行尾插,然后较小元素的指针接着向后遍历 三.代码引入 /*** Definition for singly-linked list.* struct ListNode {* int va…...

陶建国教授谈中西方文化的差异与交融
龙年到来,这个春节里,“龙”字的英文翻译引发关注,冲上了热搜,网友发现,“龙”不再翻译为“dragon”,而是龙字的谐音“loong”。原来,在西方人的眼里,龙是凶猛的怪兽,具有…...

Ps:画笔选项
画笔选项 Brush Options提供了对画笔(圆形笔刷)基本属性的控制,比如大小、硬度、间距、角度和圆度等。 Photoshop 中的快速选择工具、污点修复画笔工具、修复画笔工具、颜色替换工具、背景橡皮擦工具等的工具选项栏上提供了这种圆形笔刷选项。…...
嵌入式——Flash(W25Q64)
目录 一、初识W25Q64 1. 基本认识 2. 引脚介绍 编辑 二、W25Q64特性 1. SPI模式 2. 双输出SPI方式 三、状态寄存器 1. BUSY位 2. WEL位 3. BP2、BP1、 BP0位 4. TB位 5. 保留位 6. SRP位 四、常用操作指令 1. 写使能指令(06h) 2. 写禁…...

stm32:pwm output模块,记录一下我是用smt32,输出pwm波的记录--(实现--重要)
我是实现了输出pwm波,频率固定,占空比可以不断调整的方法,将PA0接到示波器上,可以看到是一个标准的PWM波,如图下面示波器图。 1,首先是ioc的配置 我刚开始设置的分频的倍数是7199,使得分频的太大了,示波器显示不了,最后修改为71就可以,我之前设置读取pwm也是一样的…...
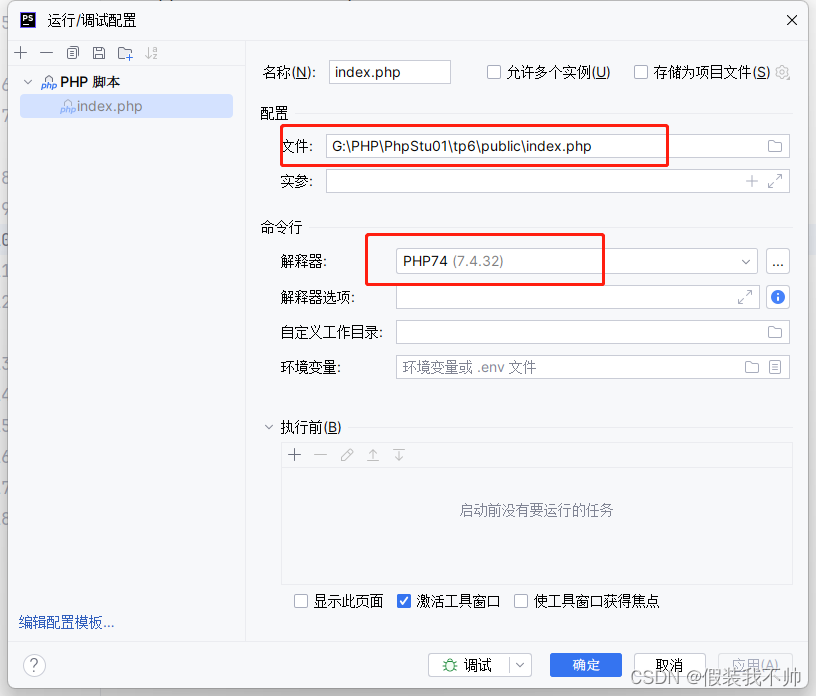
phpstrom创建thinkphp项目
安装php和composer 参考 安装phpstrom 创建项目 查看thinkphp版本 https://packagist.org/packages/topthink/think 打开所在项目编辑配置 即可调试运行...

【Linux】线程同步
线程同步 一、条件变量1. 同步概念2. 条件变量概念3. 条件变量接口(1)pthread_cond_init()(2)pthread_cond_destroy()(3)pthread_cond_wait()(4)pthread_cond_signal()(5…...

如何在多头自注意力机制的交叉学习中引入对于物理、生理、心理世界客观规律的对照验证...
要在多头自注意力机制的交叉学习中引入对于物理世界客观规律的对照验证,可以考虑以下方法: 1、引入物理模型 首先,建立一个物理模型,该模型能够描述物理世界中的客观规律。这个模型可以是已知的科学理论,也可以是通过实…...

智慧公厕:让智慧城市的公共厕所焕发“智慧活力”
智慧城市的建设已经进入了一个新的阶段,不仅仅是智慧交通、智慧环保,如今甚至连公厕都开始迎来智慧化时代。智慧公厕作为智慧城市的神经末梢,正在通过信息化、数字化和智慧化的方式,实现全方位的精细化管理。本文以智慧公厕源头专…...

vue导出word文档(图文示例)
第076个 查看专栏目录: VUE 本文章目录 示例说明示例效果图导出的文件效果截图示例源代码参数说明:重要提示:API 参考网址 示例说明 在Vue中导出Word文档,可以使用第三方库file-saver和html-docx-js。首先需要安装这两个库: npm …...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
