【JavaScript】深浅拷贝
JavaScript中复制对象有深拷贝和浅拷贝两种方式
浅拷贝:浅拷贝只复制对象的第一层属性,而不复制嵌套对象的引用。这意味着如果原始对象包含嵌套对象,浅拷贝后的对象仍然会共享这些嵌套对象的引用。可以使用`Object.assign()`或展开运算符(`...`)来进行浅拷贝。
// 浅拷贝示例 //1.使用Object.assign const originalObj = { a: 1, b: { c: 2 } }; const shallowCopy = Object.assign({}, originalObj);//2. 使⽤展开运算符 let obj1 = { a: 1, b: 2 }; let obj2 = { ...obj1 }; console.log(obj2); // { a: 1, b: 2 }深拷贝:深拷贝会递归地复制所有嵌套对象及其属性,创建一个全新的对象,不共享任何引用。这样可以确保修改深拷贝后的对象不会影响原始对象。常见的深拷贝方法包括使用`JSON.parse(JSON.stringify())`、第三方库如Lodash的`_.cloneDeep()`等。
// 深拷贝示例 const originalObj = { a: 1, b: { c: 2 } }; const deepCopy = JSON.parse(JSON.stringify(originalObj));浅拷贝只复制对象的顶层属性
而深拷贝会递归复制所有嵌套属性,确保复制后
相关文章:

【JavaScript】深浅拷贝
JavaScript中复制对象有深拷贝和浅拷贝两种方式 浅拷贝:浅拷贝只复制对象的第一层属性,而不复制嵌套对象的引用。这意味着如果原始对象包含嵌套对象,浅拷贝后的对象仍然会共享这些嵌套对象的引用。可以使用`Object.assign()`或展开运算符(`...`)来进行浅拷贝。 // 浅拷贝示…...

CH32V3xx RT-Thread RS485实现modbus rtu master
目录 1、串口配置1.1 串口初始化1.2 uart DMA 初始化1.1.3 发送函数2、agile modbus3、应用测试4、遇到的问题本文通过ch32v3xx的串口 + RS485收发器实现modbus rtu master设备。此工程中移植的RT-Thread Nano系统,详情可参看本专栏前几篇文章。 1、串口配置 串口使用重映射后…...

当网站遭到DDOS攻击怎么办?
一般网站进行上线后会经常遭到攻击,有一些攻击不怎么容易被发现,当大规模的攻击来临时,会给企业造成巨大的损失,使网站的业务下线并且访问异常,出现很多的问题。 其中DDOS攻击是最高频的一种网络攻击方式,那…...

ES6中的数组解构赋值【详解】
文章目录 1.数组的解构赋值1.1 基本用法1.2 默认值1.3更多对象解构赋值 1.数组的解构赋值 1.1 基本用法 ES6允许按照一定的模式,从数组和对象中提取值,对变量进行赋值,这被称为结构。 let [a, b, c] [1, 2, 3];如果解构不成功,…...

error An unexpected error occurred: “https://registry.npm.taobao.org
背景: 想使用yarn命令结果报错 问题原因: 原来证书到期了 http://registry.npm.taobao.org/ 把这个放到浏览器搜索的时候自动换成https://registry.npmmirror.com/ 方案: npm cache clean --forcenpm config set registry https://registry…...

react中commit工作流程
整个React工作流程可以分为两大阶段: Render阶段 Schecule Reconcile Commit阶段 注意,Render阶段是在内存中运行的,这意味者可以被打断,而commit阶段一旦开始同步执行直到完成。 Renderer工作的阶段被称为commit阶段。commit阶…...

C++类和对象-多态->多态的基本语法、多态的原理剖析、纯虚函数和抽象类、虚析构和纯虚析构
#include<iostream> using namespace std; //多态 //动物类 class Animal { public: //Speak函数就是虚函数 //函数前面加上virtual关键字,变成虚函数,那么编译器在编译的时候就不能确定函数调用了。 virtual void speak() { …...

QShortcut
一、QShortcut简介 QShortcut是Qt框架中提供的一个类,用于创建和管理键盘快捷键。它允许开发者为应用程序定义一组快捷键组合,当用户按下这些组合键时,可以触发相应的动作或事件。QShortcut的使用使得用户能够更加方便、快捷地操作应用程序&…...

浅谈语义分割、图像分类与目标检测中的TP、TN、FP、FN
语义分割 TP:正确地预测出了正类,即原本是正类,识别的也是正类 TN:正确地预测出了负类,即原本是负类,识别的也是负类 FP:错误地预测为了正类,即原本是负类,识别的是正类…...

Python基础教程:解构
嗨喽~大家好呀,这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 我们提到了字典的.items()方法会返回键值对元组的键值对元组列表: dic {key: 1, dsb: alex} print(dic.items())输出的内容为: dict_it…...
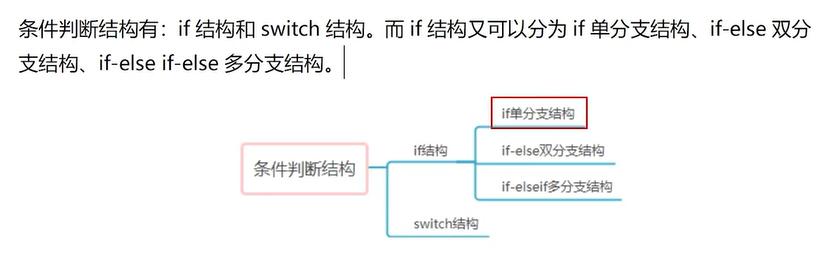
Java 学习和实践笔记(12)
这个就比较有意思了!所有的事情,拆分完之后,都有且只有这三种状态流程! //TIP To <b>Run</b> code, press <shortcut actionId"Run"/> or // click the <icon src"AllIcons.Actions.Execute&…...

学习数据结构和算法的第9天
题目讲解 移除元素 给你一个数组nums和一个值 val,你需要 原地 移除所有数值等于 val的元素,并返回移除后数组的新长度。 不要使用额外的数组空间,你必须仅使用0(1)额外空间并 原地 修改输入数组。 元素的顺序可以改变。你不需要…...

大龙谈智能内容 - 开工大吉
今天是2024年2月18日,开工第一天。 祝关注“大龙谈智能内容”的朋友龙年如龙飞天,事业步步高升!...
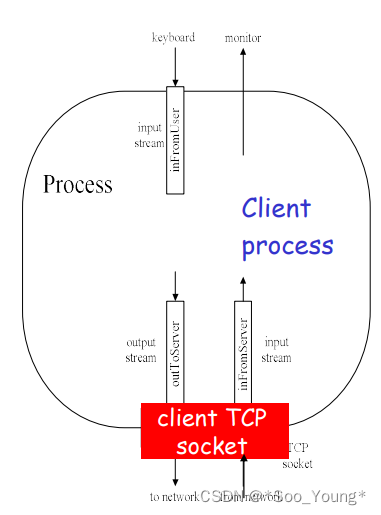
中科大计网学习记录笔记(十二):TCP 套接字编程
前前言:大家看到这一章节的时候一定不要跳过,虽然标题是编程,但实际上是对 socket 的运行机制做了详细的讨论,对理解 TCP 有很大的帮助;但是由于本节涉及到了大量的编程知识,对于一些朋友来说不是很好理解&…...

落实三大阶段目标,TRON全方位打通与BTC生态互联
2月15日,波场TRON创始人、火币HTX全球顾问委员会委员孙宇晨在X平台发布公告表示,波场TRON已正式公布比特币第二层解决方案及路线图,围绕打通比特币与波场TRON网络的跨链连接、投资开发用户友好的钱包和工具,同时与多个比特币第二层协议进行合作等重点,全方位拥抱比特币发展机遇…...
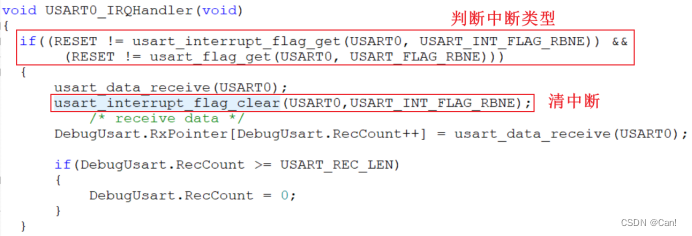
MCU中断控制
目录 一、中断相关基础知识 1、NVIC:嵌套向量中断控制器 2、可屏蔽中断和不可屏蔽中断的区别 3、中断优先级 4、常见特殊中断 二、中断相关寄存器 三、中断使用步骤: 一、中断相关基础知识 1、NVIC:嵌套向量中断控制器 (1) 它是内核的…...
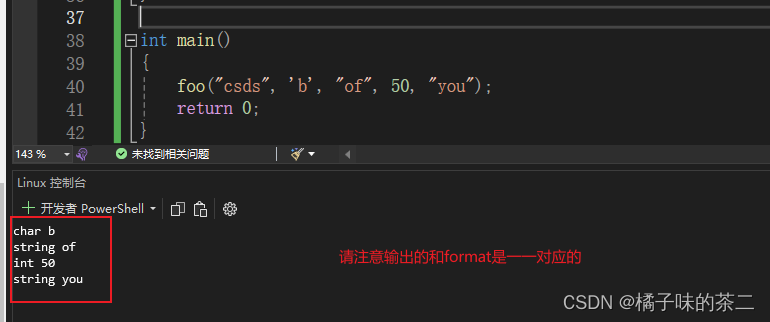
C语言中的可变参数
目录 可变参数函数原理与分析总结 实现方案1、 va_start 宏2、 va_arg 宏3、 va_end 宏 应用举例举例1:提前已知所有参数类型的简单情况举例2:通过固定参数,来动态确定可变参数类型的复杂情况 可变参数函数 在C语言中,有这样的一…...
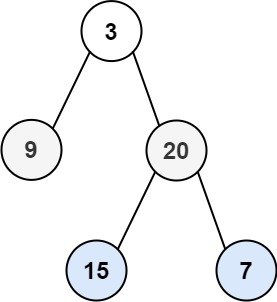
Leetcode-103. 二叉树的锯齿形层序遍历
这个年和树过不去啦啦啦! 题目: 给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。 示例 1&…...

vs code“无法与远程服务器建立连接:XHR failed.”解决办法
获取到 commit id 的方式参考: vscode通过ssh链接服务器卡在downloading with wget - 知乎 关于下载 vscode-server-linux-x64.tar.gz,浏览器打开: https://vscode.download.prss.microsoft.com/dbazure/download/stable/你的commit id/vs…...
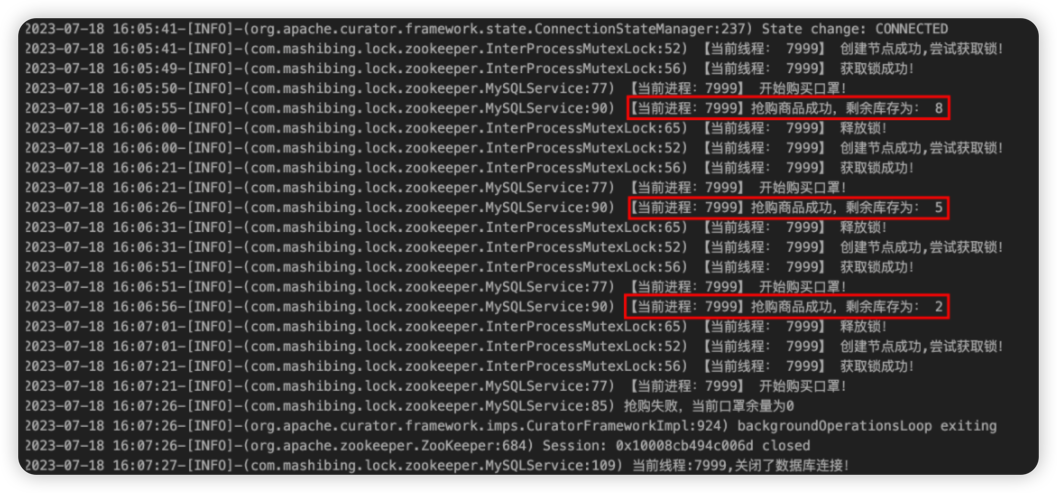
第五节 zookeeper集群与分布式锁_2
1.分布式锁概述 1.1 什么是分布式锁 1)要介绍分布式锁,首先要提到与分布式锁相对应的是线程锁。 线程锁:主要用来给方法、代码块加锁。当某个方法或代码使用锁,在同一时刻仅有一个线程执行该方法或该代码段。 线程锁只在同一J…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...
