【友塔笔试面试复盘】八边形取反问题
问题:一个八边形每条边都是0,现在有取反操作,选择一条边取反会同时把当前边和2个邻边取反(如果是0变为1,如果是1变为0)
现在问你怎么取反能使得八条边都变为1.
当时陷入了暴力递归漩涡,给出一个2的8次方复杂度的解,被薄纱了
讨论过程中发现如果决定了相邻2条边之后就可以依次决定所有边,如果成功说明这选择可行,2条边一共就4种情况,取取,不取取,取不取,不取不取,挨个试就行,如果都不行就是不行,该复杂度就只有O(n),太漂亮了,过去了一年多,现在决定代码实现一下
ps:每一条边也只会被三条边影响
#include<iostream>
#include<vector>
#include<map>
using namespace std;void changenumber(int &i) {if (i != 0 && i != 1)return;if (i == 0)i = 1;else if (i == 1)i = 0;
}
void doback(int a[], int i,int n) {if (i >= n)return;if (i == 0) {changenumber(a[n - 1]);changenumber(a[0]);changenumber(a[1]);}else if (i == n - 1) {changenumber(a[n - 1]);changenumber(a[n-2]);changenumber(a[0]);}else {changenumber(a[i-1]);changenumber(a[i]);changenumber(a[i+1]);}
}void printnums(int a[],int n) {for (int i = 0; i < n; i++) {printf("%d ", a[i]);}printf("\n");
}void printstrings(string a[], int n) {for (int i = 0; i < n; i++) {printf("%s \n", a[i]);}
}int Finalnums(int a[],int flag[], int i, int j,int ido,int jdo,int n) {if (ido) {doback(a, i, n);flag[i] = 2;}else {flag[i] = 1;}if (jdo) {doback(a, j, n);flag[j] = 2;}else {flag[j] = 1;}j++;while (j < n) {if (a[j-1] == 0) {doback(a, j, n);flag[j] = 2;}else {flag[j] = 1;}j++;}j = 0;if (i == 0)return a[n-1];if (a[n - 1] == 0) {doback(a, j, n);flag[j] = 2;}else {flag[j] = 1;}j++;while (j < i) {if (a[j - 1] == 0) {doback(a, j, n);flag[j] = 2;}else {flag[j] = 1;}j++;}return a[j - 1];
}void resetnums(int a[], int n) {for (int i = 0; i < n; i++) {a[i] = 0;}
}
int main() {int a[8] = { 0 };int flag[8] = { 0 };if (Finalnums(a, flag, 0, 1, 0, 0, 8)) {printf("0不取,1不取就可以满足要求:");printnums(a, 8);printnums(flag, 8);resetnums(a, 8);resetnums(flag, 8);}if (Finalnums(a, flag, 0, 1, 1, 0, 8)) {printf("0取,1不取就可以满足要求:");printnums(a, 8);printnums(flag, 8);resetnums(a, 8);resetnums(flag, 8);}if (Finalnums(a, flag, 0, 1, 0, 1, 8)) {printf("0不取,1取就可以满足要求:");printnums(a, 8);printnums(flag, 8);resetnums(a, 8);resetnums(flag, 8);}if (Finalnums(a, flag, 0, 1, 1, 1, 8)) {printf("0取,1取就可以满足要求:");printnums(a, 8);printnums(flag, 8);resetnums(a, 8);resetnums(flag, 8);}
}
有明确思路都写了一小时,属实有点难度了

想了想,第二种真就随便想啊
依稀记得面试官说考察候选人智力,焯!
相关文章:

【友塔笔试面试复盘】八边形取反问题
问题:一个八边形每条边都是0,现在有取反操作,选择一条边取反会同时把当前边和2个邻边取反(如果是0变为1,如果是1变为0) 现在问你怎么取反能使得八条边都变为1. 当时陷入了暴力递归漩涡,给出一个…...

GB 18585-2023 壁纸中有害物质限量
壁纸/墙布因其色彩多样,图案丰富,施工方便,价格便宜等多种优势,广泛应用于室内装修材料,在国内,日本,欧美等地区非常普及。 GB 18585-2023壁纸中有害物质限量测试项目: 测试项目 测…...

全面的ASP.NET Core Blazor简介和快速入门
前言 因为咱们的MongoDB入门到实战教程Web端准备使用Blazor来作为前端展示UI,本篇文章主要是介绍Blazor是一个怎样的Web UI框架,其优势和特点在哪?并带你快速入门上手ASP.NET Core Blazor(当然这个前提是你要有一定的C#编程基础的情况&#x…...

HGAME 2024 WEEK2 Crypto WP
前言 我很菜,有没做出来的题目,带*号题为复现。 midRSA 题目: from Crypto.Util.number import * from secret import flagdef padding(flag):return flagb\xff*(64-len(flag))flagpadding(flag) mbytes_to_long(flag) pgetPrime(512) qg…...

Postman轻松签名,让SHA256withRSA保驾护航!
前言 在接口测试中,我们经常需要对请求进行签名,以保证数据的安全性。而SHA256withRSA是一种较为常见的签名算法,它可以使用私钥对数据进行签名,使用公钥进行验签。 但是,实现该算法签名可能会涉及到一些繁琐的操作&…...

C#面:简述装箱和拆箱
在C#中,装箱(boxing)和拆箱(unboxing)是用于在值类型和引用类型之间进行转换的过程。 装箱:(Boxing) 是将值类型转换为引用类型的过程。 将一个值类型赋值给一个对象类型时&#x…...
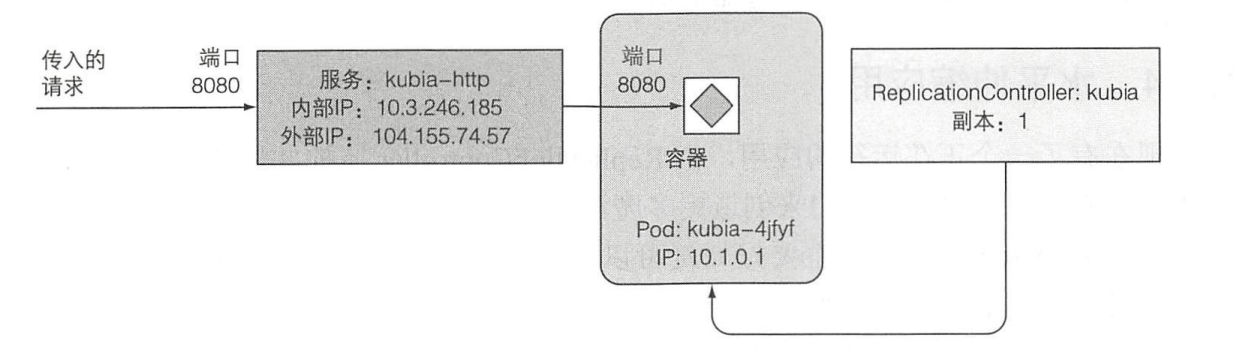
【Kubernetes in Action笔记】1.快速开始
在Kubernetes上运行一个程序 基础运行环境 当前的运行环境为使用虚拟机构建的单master集群。 [rootk8s-master ~]# kubectl get nodes NAME STATUS ROLES AGE VERSION k8s-master Ready control-plane 109d v1.27.1 k8s-node1 Ready …...

踩坑实录(Fourth Day)
今天开工了,其实还沉浸在过年放假的喜悦中……今天在自己写 Vue3 的项目,虽说是跟着 B 站在敲,但是依旧是踩了一些个坑,就离谱……照着敲都能踩到坑,我也是醉了…… 此为第四篇(2024 年 02 月 18 日&#x…...
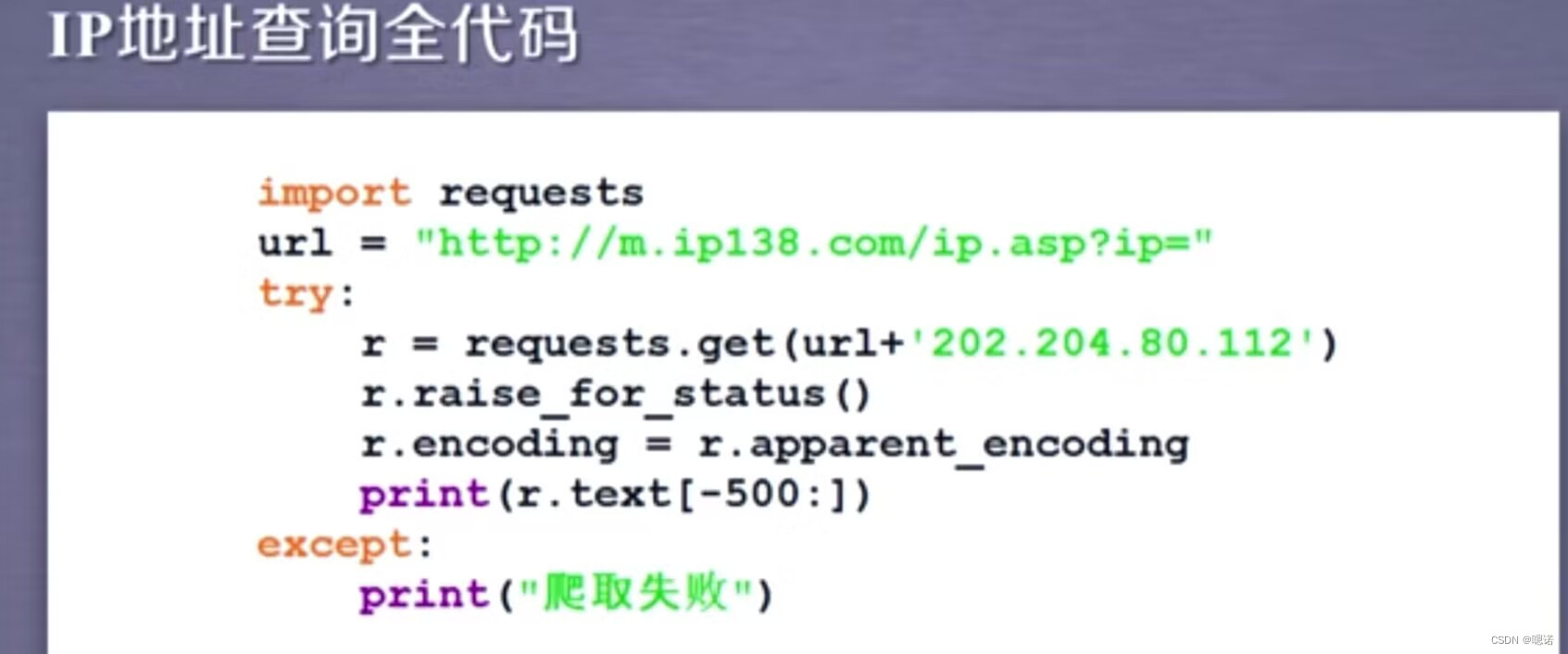
【python】网络爬虫与信息提取--requests库
导学 当一个软件想获得数据,那么我们只有把网站当成api就可以 requests库:自动爬取HTML页面,自动网络请求提交 robots协议:网络爬虫排除标准(网络爬虫的规则) beautiful soup库:解析HTML页面 工具&…...
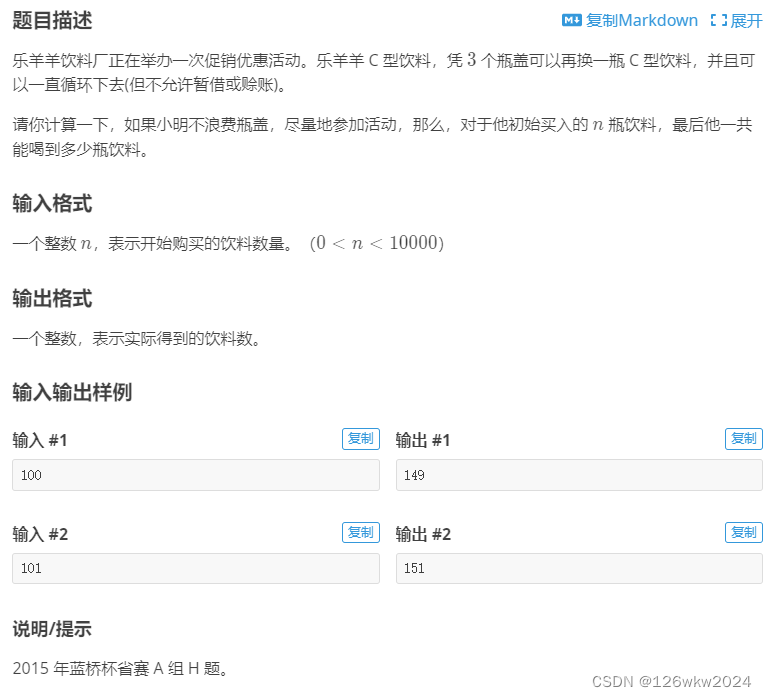
洛谷 P8627 [蓝桥杯 2015 省 A] 饮料换购
参考代码and代码解读 #include <bits/stdc.h> using namespace std; int main() { int n; scanf("%d", &n); int dr;//drdrink; dr n;//把drink赋值于n; while (n > 2) {//剩余的总瓶盖数要大于二,才能换得下一瓶饮料; dr n…...

Academic Inquiry|投稿状态分享(ACS,Wiley,RSC,Elsevier,MDPI,Springer Nature出版社)
作为科研人员,我们经常会面临着向学术期刊投稿的问题。一般来说,期刊的投稿状态会在官方网站上进行公示,我们可以通过期刊的官方网站或者投稿系统查询到我们投稿的论文的状态,对于不同的期刊在投稿系统中会有不同的显示。 说明&am…...
)
1+X运维试题样卷C卷(初级)
云计算C卷 单选题(200分) 1.在OSI模型中,HTTP协议工作在第()层,交换机工作在第()层。(10分) (答案未做:0分) A、7/3 B、7/2 (正确答案) C、6/3 D、6/2 2.Linux有三个查看文件的命令,若希望在查看文件内容过程中可以用光标上下移动来查看文件内容,应使用命令。(10分…...
Spring的控制反转(设计原则)与依赖注入(设计模式))
Spring学习笔记(二)Spring的控制反转(设计原则)与依赖注入(设计模式)
一、控制反转:缩写IoC 是一种设计原则,降低程序代码之间的耦合度 对象由Ioc容器统一管理,当程序需要使用对象时直接从IoC容器中获取。这样对象的控制权就从应用程序转移到了IoC容器 二、依赖注入:缩写DI 依赖注入是一种消除类之…...
MySQL 基础知识(四)之表操作
目录 1 约束 2 查看已有表 3 创建表 4 查看表结构 5 修改表 6 删除表 1 约束 主键约束 primary key:唯一,标识表中的一行数据,此列的值不可重复,且不能为 NULL,此外,可以多个列组成主键唯一约束 uniq…...

计算机网络——10FTP
FTP FTP:文件传输协议 向远程主机上传输文件或从远程主机接收文件客户/服务器模式 客户端:发起传输的一方服务器:远程主机 ftp:RFC 959ftp服务器:端口号为21 FTP:控制连接与数据连接分开 控制连接 FTP客户端与FTP服…...

javascript中的this指向
文章目录 探索 JavaScript 中的神奇之谜:this关键字解析this 是什么?为何 this如此重要?this 的工作原理实例解析默认绑定隐式绑定显式绑定new 绑定 探索 JavaScript 中的神奇之谜:this关键字解析 JavaScript,作为一门…...
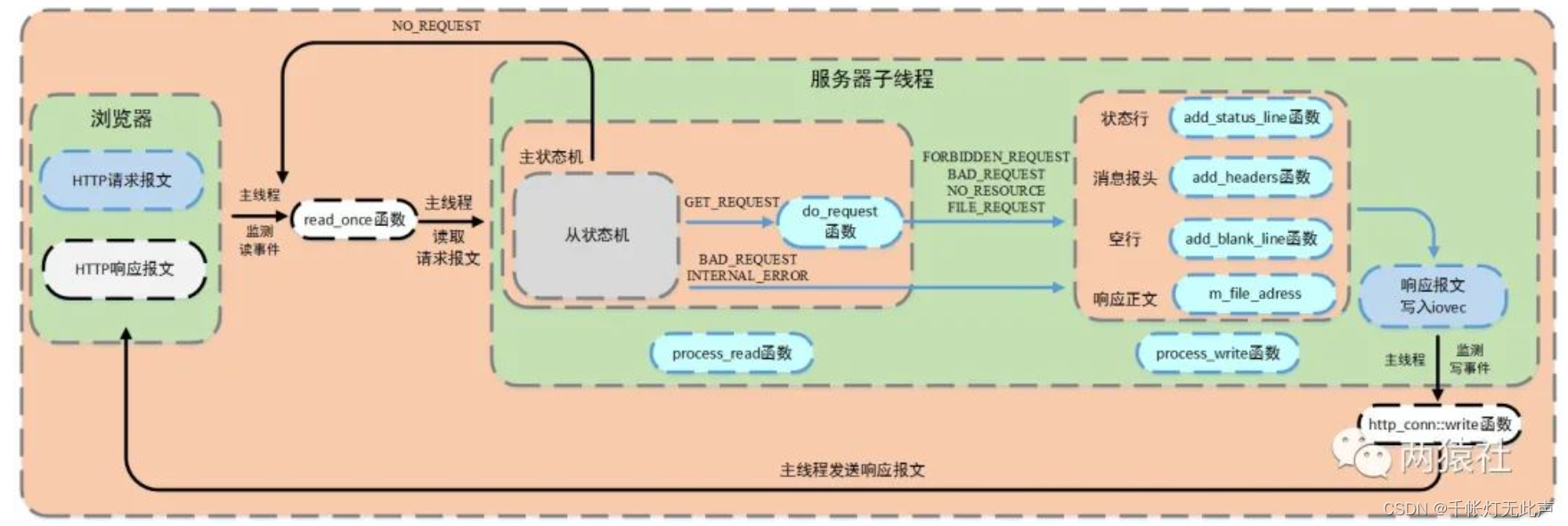
WebServer 之 http连接处理(下)
目录 ✊请求报文--解析 流程图 && 状态机 状态机 -- 状态转移图 主状态机 从状态机 http 报文解析 HTTP_CODE 含义 从状态机 逻辑 主状态机 逻辑 🐞请求报文--响应 基础API stat mmap iovec writev 流程图 HTTP_CODE 含义(2) 代码分析 …...

Android电量相关知识
关于作者:CSDN内容合伙人、技术专家, 从零开始做日活千万级APP。 专注于分享各领域原创系列文章 ,擅长java后端、移动开发、商业变现、人工智能等,希望大家多多支持。 目录 一、导读二、概览三、 查看耗电情况3.1 注册广播 ACTION…...
【Java多线程】线程中几个常见的属性以及状态
目录 Thread的几个常见属性 1、Id 2、Name名称 3、State状态 4、Priority优先级 5、Daemon后台线程 6、Alive存活 Thread的几个常见属性 1、Id ID 是线程的唯一标识,由系统自动分配,不同线程不会重复。 2、Name名称 用户定义的名称。该名称在各种…...

鸿蒙OS跨进程IPC与RPC通信
一、IPC与RPC通信概述 基本概念 IPC(Inter-Process Communication)与RPC(Remote Procedure Call)用于实现跨进程通信,不同的是前者使用Binder驱动,用于设备内的跨进程通信,后者使用软总线驱动…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...

【版本控制】GitHub Desktop 入门教程与开源协作全流程解析
目录 0 引言1 GitHub Desktop 入门教程1.1 安装与基础配置1.2 核心功能使用指南仓库管理日常开发流程分支管理 2 GitHub 开源协作流程详解2.1 Fork & Pull Request 模型2.2 完整协作流程步骤步骤 1: Fork(创建个人副本)步骤 2: Clone(克隆…...
