Leetcode 392 判断子序列
题意理解:
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,
"ace"是"abcde"的一个子序列,而"aec"不是)。即判断s和t是否存在一个最长公共子序列,且该最长公共子序列==s
这里采用一个动态规划的思路求解最长公共子序列,其长度==s.size
解题思路:
(1) 定义dp数组
定义二维dp数组,dp[i][j]表示s第i个元素前,t第j个元素前最长公共子序列。
i,j指示的是元素之间的位置
其i属于[0,s.size+1], j属于[0,t.size+1]
(2)初始化
dp[0][j]和dp[i][0]表示第一行第一列,其都是用一个空数组和一个非空数组求其最长公共给子序列,所以全部初始化为0.
其余元素初始化为0,后续操作会被覆盖掉。
(3)递推公式
if(s[i-1]==t[j-1]) dp[i][j]=dp[i-1][j-1]+1
else dp[i][j]=max(dp[i][j-1],dp[i-1][j])
(4)返回
if(dp[s.size-1][t.size-1]==s.size) return true;
else return false;
1.动态规划
public boolean isSubsequence(String s, String t) {int[][] dp=new int[s.length()+1][t.length()+1];for(int i=0;i<s.length();i++){Arrays.fill(dp[i],0);}for(int i=1;i<=s.length();i++){for(int j=1;j<=t.length();j++){if(s.charAt(i-1)==t.charAt(j-1)){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);}}}if(dp[s.length()][t.length()]==s.length()) return true;return false;}2.分析
时间复杂度:O(n^2)
空间复杂度:O(n^2)
相关文章:

Leetcode 392 判断子序列
题意理解: 给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde&quo…...
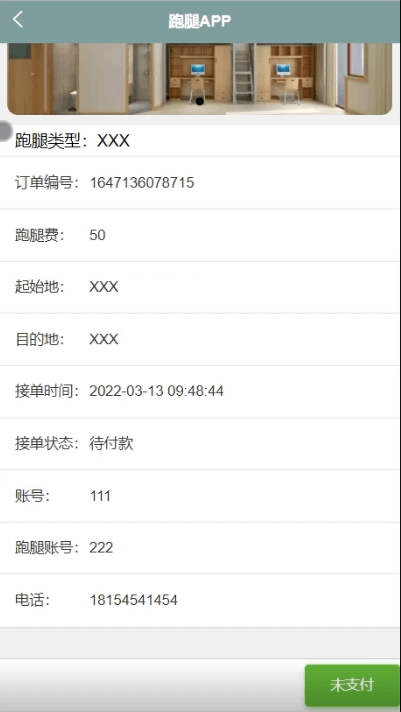
基于微信小程序的校园跑腿系统的研究与实现,附源码
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12w、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...

VTK Python PyQt 监听键盘 控制 Actor 移动 变色
KeyPressInteractorStyle 在vtk 中有时我们需要监听 键盘或鼠标做一些事; 1. 创建 Actor; Sphere vtk.vtkSphereSource() Sphere.SetRadius(10)mapper vtk.vtkPolyDataMapper() mapper.SetInputConnection(Sphere.GetOutputPort()) actor vtk.vtkAc…...

力扣 第 124 场双周赛 解题报告 | 珂学家 | 非常规区间合并
前言 整体评价 T4的dp解法没想到,走了一条"不归路", 这个区间合并解很特殊,它是带状态的,而且最终的正解也是基于WA的case,慢慢理清的。 真心不容易,太难了。 T1. 相同分数的最大操作数目 I 思路: 模拟 c…...
)
2024年华为OD机试真题-生成哈夫曼树-Java-OD统一考试(C卷)
题目描述: 给定长度为n的无序的数字数组,每个数字代表二叉树的叶子节点的权值,数字数组的值均大于等于1。请完成一个函数,根据输入的数字数组,生成哈夫曼树,并将哈夫曼树按照中序遍历输出。 为了保证输出的二叉树中序遍历结果统一,增加以下限制:二叉树节点中,左节点权…...
 —— 前端要学的测试课 从Jest入门到TDD BDD双实战(六))
【实战】二、Jest难点进阶(二) —— 前端要学的测试课 从Jest入门到TDD BDD双实战(六)
文章目录 一、Jest 前端自动化测试框架基础入门二、Jest难点进阶2.mock 深入学习 学习内容来源:Jest入门到TDD/BDD双实战_前端要学的测试课 相对原教程,我在学习开始时(2023.08)采用的是当前最新版本: 项版本babel/co…...
【Jmeter】JDK及Jmeter的安装部署及简单配置)
(一)【Jmeter】JDK及Jmeter的安装部署及简单配置
JDK的安装和环境变量配置 对于Linux、Mac和Windows系统,JDK的安装和环境变量配置方法略有不同。以下是针对这三种系统的详细步骤: 对于Linux系统: 下载适合Linux系统的JDK安装包,可以选择32位或64位的版本。 将JDK的安装包放置在服务器下,创建一个新的文件夹来存储JDK,…...
HAL/LL/STD STM32 U8g2库 +I2C SSD1306/sh1106 WouoUI磁贴案例
HAL/LL/STD STM32 U8g2库 I2C SSD1306/sh1106 WouoUI磁贴案例 📍基于STM32F103C8T6 LL库驱动版本:https://gitee.com/chcsx/platform-test/tree/master/MDK-ARM🎬视频演示: WouoUI移植磁贴案例,新增确认弹窗 …...

手机如何改自己的ip地址
在现如今的数码时代,手机已经成为人们生活中不可或缺的一部分。然而,有时候我们可能需要改变手机的IP地址来实现一些特定的需求。本文将向大家介绍如何改变手机的IP地址,帮助大家更好地应对各种网络问题。 更改手机IP地址的原因:…...

ajax函数库axios基本使用
ajax函数库Axios基本使用 简介:Axios 对原生的Ajax进行了封装,简化书写,快速开发。 官网:https://www.axios-http.cn/ Axios使用步骤 引入Axios的js文件(参考官网)使用Axios发送请求,获取相应结果 <script src"https:…...
)
【nginx实践连载-4】彻底卸载Nginx(Ubuntu)
步骤1:停止Nginx服务 打开终端(Terminal)。停止Nginx服务:sudo systemctl stop nginx步骤2:卸载Nginx软件包 运行以下命令卸载Nginx软件包:sudo apt purge nginx nginx-common nginx-core步骤3࿱…...

究极小白如何自己搭建一个自动发卡网站-独角数卡
首页 | 十画IOSIDshihuaid.cn/编辑 如果你也是跟我一样,什么都不懂,也想要搭建一个自己的自动发卡网站,可以参考一下我的步骤,不难,主要就是细心,一步步来一定成功!! 独角数卡: 举个例子:独角数卡就是一个店面,而且里面帮你装修好了,而你要做的就是把开店之…...

Java_方法(重载方法签名等详解)
在之前我们学习C语言时,当我们想要重复使用某段代码的功能时,我们会将这段代码定义为一个函数,而在java中我们把这段重复使用的代码叫做方法。 方法的定义 类体的内容分为变量的声明和方法的定义,方法的定义包括两部分࿱…...
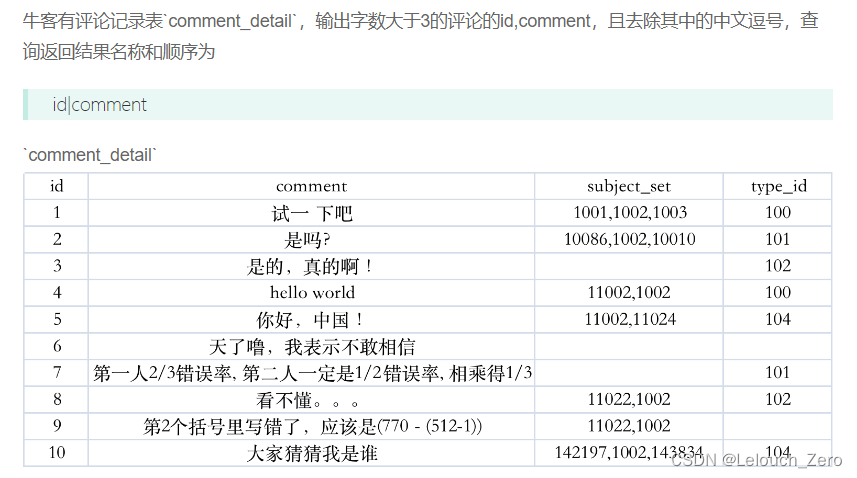
VQ35 评论替换和去除(char_length()和replace函数的使用)
代码 select id ,replace(comment,,,) as comment from comment_detail where char_length(comment)>3知识点 要注意替换的是中文逗号 由于题目说的是汉字长度大于3,所以这里就要使用char_length()而不是length() char_length():单位为字…...

【MySQL】学习多表查询和笛卡尔积
🌈个人主页: Aileen_0v0 🔥热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法 💫个人格言:“没有罗马,那就自己创造罗马~” #mermaid-svg-N8PeTKG6uLu4bJuM {font-family:"trebuchet ms",verdana,arial,sans-serif;font-siz…...

RabbitMQ实现延迟消息的方式-死信队列、延迟队列和惰性队列
当一条消息因为一些原因无法被成功消费,那么这这条消息就叫做死信,如果包含死信的队列配置了dead-letter-exchange属性指定了一个交换机,队列中的死信都会投递到这个交换机内,这个交换机就叫死信交换机,死信交换机再绑…...
【运维测试】测试理论+工具总结笔记第1篇:测试理论的主要内容(已分享,附代码)
本系列文章md笔记(已分享)主要讨论测试理论测试工具相关知识。Python测试理论的主要内容,掌握软件测试的基本流程,知道软件测试的V和W模型的优缺点,掌握测试用例设计的要素,掌握等价类划分法、边界值法、因…...
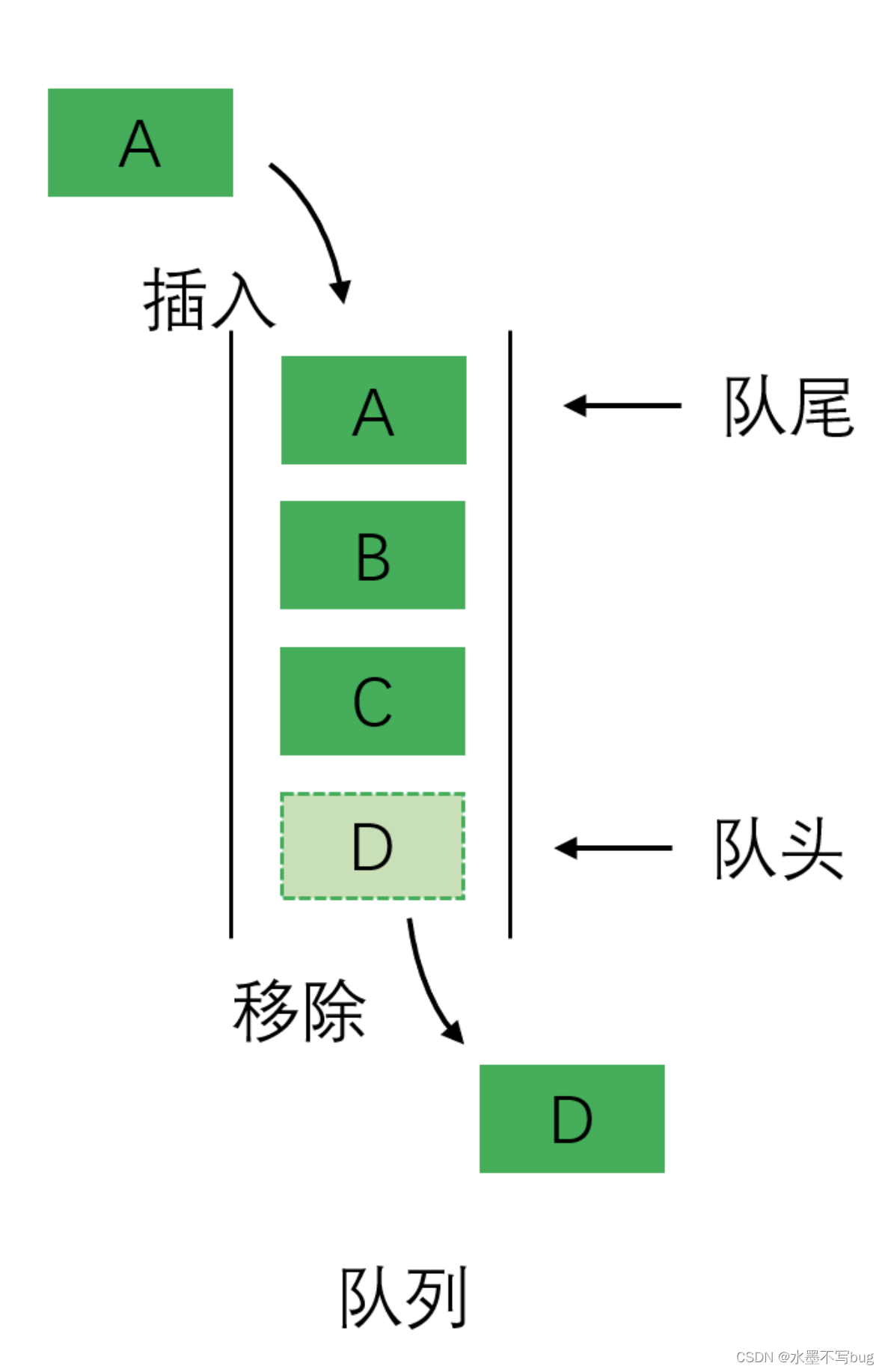
【C语言】实现队列
目录 (一)队列 (二)头文件 (三) 功能实现 (1)初始化 (2) 销毁队列 (3) 入队 (4)出队 (5&a…...

【友塔笔试面试复盘】八边形取反问题
问题:一个八边形每条边都是0,现在有取反操作,选择一条边取反会同时把当前边和2个邻边取反(如果是0变为1,如果是1变为0) 现在问你怎么取反能使得八条边都变为1. 当时陷入了暴力递归漩涡,给出一个…...

GB 18585-2023 壁纸中有害物质限量
壁纸/墙布因其色彩多样,图案丰富,施工方便,价格便宜等多种优势,广泛应用于室内装修材料,在国内,日本,欧美等地区非常普及。 GB 18585-2023壁纸中有害物质限量测试项目: 测试项目 测…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...
