力扣 第 124 场双周赛 解题报告 | 珂学家 | 非常规区间合并
前言

整体评价
T4的dp解法没想到,走了一条"不归路", 这个区间合并解很特殊,它是带状态的,而且最终的正解也是基于WA的case,慢慢理清的。
真心不容易,太难了。
T1. 相同分数的最大操作数目 I
思路: 模拟
class Solution {public int maxOperations(int[] nums) {int n = nums.length;int res = 1;for (int i = 2; i + 1 < n; i+= 2) {if (nums[i] + nums[i + 1] == nums[0] + nums[1]) {res++;} else {break;}}return res;}}
T2. 进行操作使字符串为空
思路: 模拟
感觉有点绕
class Solution {public String lastNonEmptyString(String s) {List<Integer> []g = new List[26];Arrays.setAll(g, x->new ArrayList<>());for (int i = 0; i < s.length(); i++) {int p = s.charAt(i) - 'a';g[p].add(i);}int mz = 0;for (int i = 0; i < 26; i++) {mz = Math.max(g[i].size(), mz);}List<int[]> lasts = new ArrayList<>();for (int i = 0; i < 26; i++) {if (g[i].size() == mz) {lasts.add(new int[] {i, g[i].get(mz - 1)});}}Collections.sort(lasts, Comparator.comparing(x -> x[1]));StringBuilder sb = new StringBuilder();for (int[] e: lasts) {sb.append((char)(e[0] + 'a'));}return sb.toString();}
}
T3. 相同分数的最大操作数目 II
思路: 枚举+区间DP
因为要求和相等,所以枚举最初的和,然后记忆化搜索一下就出来了
class Solution {int dfs(Integer[][] dp, int[] nums, int s, int e, int v) {if (s >= e) return 0;if (dp[s][e] != null) return dp[s][e];int res = 0;if (nums[s] + nums[e] == v) {int r = dfs(dp, nums, s + 1, e - 1, v);res = Math.max(res, r + 1);}if (nums[s] + nums[s + 1] == v) {int r = dfs(dp, nums, s + 2, e, v);res = Math.max(res, r + 1);} if (nums[e - 1] + nums[e] == v) {int r = dfs(dp, nums, s, e - 2, v);res = Math.max(res, r + 1);}return dp[s][e] = res;}public int maxOperations(int[] nums) {int n = nums.length;int r1 = dfs(new Integer[n][n], nums, 1, n - 2, nums[0] + nums[n - 1]);int r2 = dfs(new Integer[n][n], nums, 2, n - 1, nums[0] + nums[1]);int r3 = dfs(new Integer[n][n], nums, 0, n - 3, nums[n - 2] + nums[n - 1]);return Math.max(r1, Math.max(r2, r3)) + 1;}}
T4. 修改数组后最大化数组中的连续元素数目
思路: 区间合并
但是这个区间合并很特别,是带状态的
class Solution {static class Segment {int start, end;int lastStart, full;public Segment(int start, int end, int lastStart, int full) {this.start = start;this.end = end;this.lastStart = lastStart;this.full = full;}}public int maxSelectedElements(int[] nums) {int n = nums.length;Arrays.sort(nums);List<Segment> segs = new ArrayList<>();int i = 0;while (i < n) {int flag = 0;int j = i + 1;while (j < n && nums[j - 1] + 1 >= nums[j]) {if (nums[j - 1] == nums[j]) {flag = 1;}j++;}segs.add(new Segment(nums[i], nums[j - 1], nums[i], flag));i = j;}Segment pre = null;int res = 0;for (Segment seg: segs) {if (pre == null) {pre = new Segment(seg.start, seg.end, seg.start, seg.full);} else {if (pre.end + 2 == seg.start) {if (pre.full == 1) {pre = new Segment(pre.start, seg.end, seg.start, seg.full);} else {pre = new Segment(pre.lastStart + 1, seg.end, seg.start, seg.full);}} else {pre = new Segment(seg.start, seg.end, seg.start, seg.full);}}res = Math.max(res, pre.end - pre.start + 1);if (pre.full == 1) {res = Math.max(res, pre.end - pre.start + 2);}}return res;}}
写在最后
相关文章:

力扣 第 124 场双周赛 解题报告 | 珂学家 | 非常规区间合并
前言 整体评价 T4的dp解法没想到,走了一条"不归路", 这个区间合并解很特殊,它是带状态的,而且最终的正解也是基于WA的case,慢慢理清的。 真心不容易,太难了。 T1. 相同分数的最大操作数目 I 思路: 模拟 c…...
)
2024年华为OD机试真题-生成哈夫曼树-Java-OD统一考试(C卷)
题目描述: 给定长度为n的无序的数字数组,每个数字代表二叉树的叶子节点的权值,数字数组的值均大于等于1。请完成一个函数,根据输入的数字数组,生成哈夫曼树,并将哈夫曼树按照中序遍历输出。 为了保证输出的二叉树中序遍历结果统一,增加以下限制:二叉树节点中,左节点权…...
 —— 前端要学的测试课 从Jest入门到TDD BDD双实战(六))
【实战】二、Jest难点进阶(二) —— 前端要学的测试课 从Jest入门到TDD BDD双实战(六)
文章目录 一、Jest 前端自动化测试框架基础入门二、Jest难点进阶2.mock 深入学习 学习内容来源:Jest入门到TDD/BDD双实战_前端要学的测试课 相对原教程,我在学习开始时(2023.08)采用的是当前最新版本: 项版本babel/co…...
【Jmeter】JDK及Jmeter的安装部署及简单配置)
(一)【Jmeter】JDK及Jmeter的安装部署及简单配置
JDK的安装和环境变量配置 对于Linux、Mac和Windows系统,JDK的安装和环境变量配置方法略有不同。以下是针对这三种系统的详细步骤: 对于Linux系统: 下载适合Linux系统的JDK安装包,可以选择32位或64位的版本。 将JDK的安装包放置在服务器下,创建一个新的文件夹来存储JDK,…...
HAL/LL/STD STM32 U8g2库 +I2C SSD1306/sh1106 WouoUI磁贴案例
HAL/LL/STD STM32 U8g2库 I2C SSD1306/sh1106 WouoUI磁贴案例 📍基于STM32F103C8T6 LL库驱动版本:https://gitee.com/chcsx/platform-test/tree/master/MDK-ARM🎬视频演示: WouoUI移植磁贴案例,新增确认弹窗 …...

手机如何改自己的ip地址
在现如今的数码时代,手机已经成为人们生活中不可或缺的一部分。然而,有时候我们可能需要改变手机的IP地址来实现一些特定的需求。本文将向大家介绍如何改变手机的IP地址,帮助大家更好地应对各种网络问题。 更改手机IP地址的原因:…...

ajax函数库axios基本使用
ajax函数库Axios基本使用 简介:Axios 对原生的Ajax进行了封装,简化书写,快速开发。 官网:https://www.axios-http.cn/ Axios使用步骤 引入Axios的js文件(参考官网)使用Axios发送请求,获取相应结果 <script src"https:…...
)
【nginx实践连载-4】彻底卸载Nginx(Ubuntu)
步骤1:停止Nginx服务 打开终端(Terminal)。停止Nginx服务:sudo systemctl stop nginx步骤2:卸载Nginx软件包 运行以下命令卸载Nginx软件包:sudo apt purge nginx nginx-common nginx-core步骤3࿱…...

究极小白如何自己搭建一个自动发卡网站-独角数卡
首页 | 十画IOSIDshihuaid.cn/编辑 如果你也是跟我一样,什么都不懂,也想要搭建一个自己的自动发卡网站,可以参考一下我的步骤,不难,主要就是细心,一步步来一定成功!! 独角数卡: 举个例子:独角数卡就是一个店面,而且里面帮你装修好了,而你要做的就是把开店之…...

Java_方法(重载方法签名等详解)
在之前我们学习C语言时,当我们想要重复使用某段代码的功能时,我们会将这段代码定义为一个函数,而在java中我们把这段重复使用的代码叫做方法。 方法的定义 类体的内容分为变量的声明和方法的定义,方法的定义包括两部分࿱…...
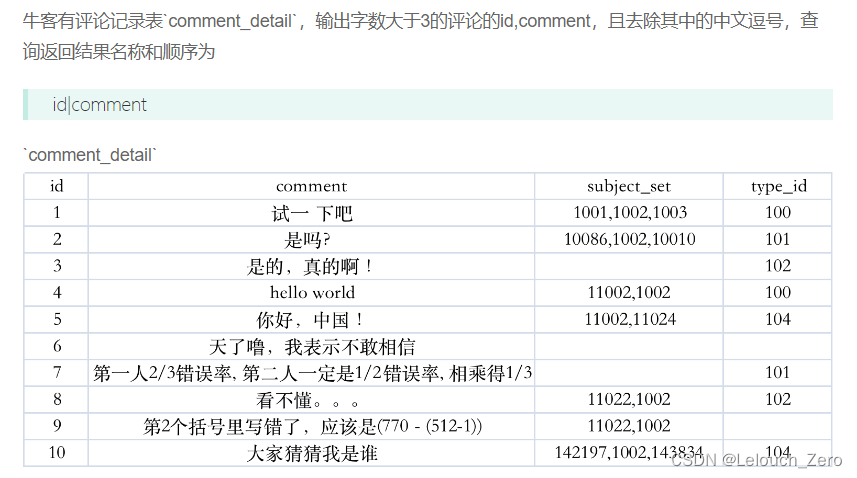
VQ35 评论替换和去除(char_length()和replace函数的使用)
代码 select id ,replace(comment,,,) as comment from comment_detail where char_length(comment)>3知识点 要注意替换的是中文逗号 由于题目说的是汉字长度大于3,所以这里就要使用char_length()而不是length() char_length():单位为字…...

【MySQL】学习多表查询和笛卡尔积
🌈个人主页: Aileen_0v0 🔥热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法 💫个人格言:“没有罗马,那就自己创造罗马~” #mermaid-svg-N8PeTKG6uLu4bJuM {font-family:"trebuchet ms",verdana,arial,sans-serif;font-siz…...

RabbitMQ实现延迟消息的方式-死信队列、延迟队列和惰性队列
当一条消息因为一些原因无法被成功消费,那么这这条消息就叫做死信,如果包含死信的队列配置了dead-letter-exchange属性指定了一个交换机,队列中的死信都会投递到这个交换机内,这个交换机就叫死信交换机,死信交换机再绑…...
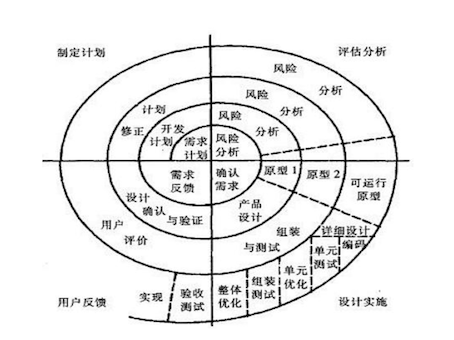
【运维测试】测试理论+工具总结笔记第1篇:测试理论的主要内容(已分享,附代码)
本系列文章md笔记(已分享)主要讨论测试理论测试工具相关知识。Python测试理论的主要内容,掌握软件测试的基本流程,知道软件测试的V和W模型的优缺点,掌握测试用例设计的要素,掌握等价类划分法、边界值法、因…...
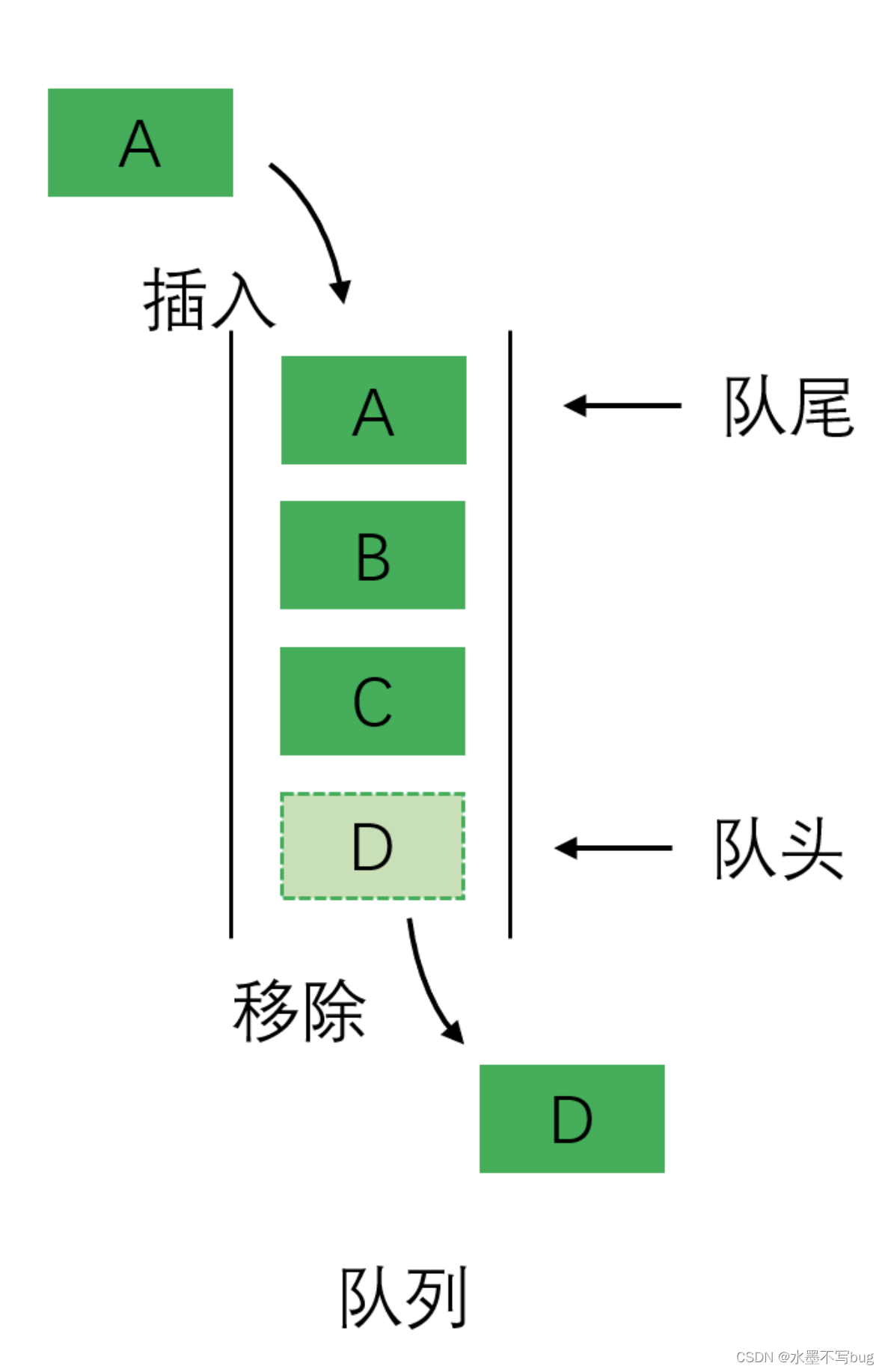
【C语言】实现队列
目录 (一)队列 (二)头文件 (三) 功能实现 (1)初始化 (2) 销毁队列 (3) 入队 (4)出队 (5&a…...

【友塔笔试面试复盘】八边形取反问题
问题:一个八边形每条边都是0,现在有取反操作,选择一条边取反会同时把当前边和2个邻边取反(如果是0变为1,如果是1变为0) 现在问你怎么取反能使得八条边都变为1. 当时陷入了暴力递归漩涡,给出一个…...

GB 18585-2023 壁纸中有害物质限量
壁纸/墙布因其色彩多样,图案丰富,施工方便,价格便宜等多种优势,广泛应用于室内装修材料,在国内,日本,欧美等地区非常普及。 GB 18585-2023壁纸中有害物质限量测试项目: 测试项目 测…...

全面的ASP.NET Core Blazor简介和快速入门
前言 因为咱们的MongoDB入门到实战教程Web端准备使用Blazor来作为前端展示UI,本篇文章主要是介绍Blazor是一个怎样的Web UI框架,其优势和特点在哪?并带你快速入门上手ASP.NET Core Blazor(当然这个前提是你要有一定的C#编程基础的情况&#x…...

HGAME 2024 WEEK2 Crypto WP
前言 我很菜,有没做出来的题目,带*号题为复现。 midRSA 题目: from Crypto.Util.number import * from secret import flagdef padding(flag):return flagb\xff*(64-len(flag))flagpadding(flag) mbytes_to_long(flag) pgetPrime(512) qg…...

Postman轻松签名,让SHA256withRSA保驾护航!
前言 在接口测试中,我们经常需要对请求进行签名,以保证数据的安全性。而SHA256withRSA是一种较为常见的签名算法,它可以使用私钥对数据进行签名,使用公钥进行验签。 但是,实现该算法签名可能会涉及到一些繁琐的操作&…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
