【递归】【后续遍历】【迭代】【队列】Leetcode 101 对称二叉树
【递归】【后续遍历】Leetcode 101 对称二叉树
- 解法一: 递归:后序遍历 左右中
- 解法二: 迭代法,用了单端队列
---------------🎈🎈对称二叉树 题目链接🎈🎈-------------------
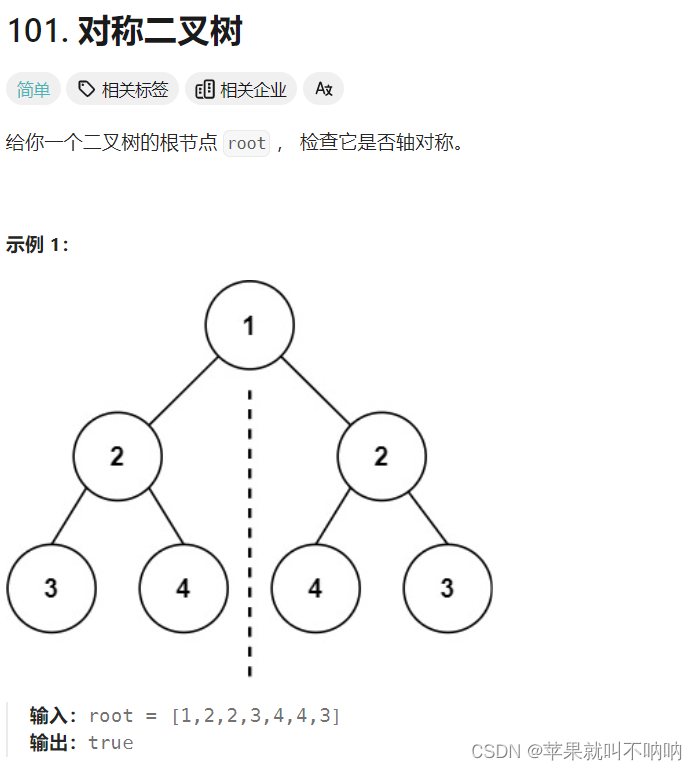
解法一: 递归:后序遍历 左右中
时间复杂度O(N)
空间复杂度O(N)
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isSymmetric(TreeNode root) {// 递归return compare(root.left, root.right);}public boolean compare(TreeNode left, TreeNode right){ // 确定递归的参数和返回值if(left == null && right==null){return true;}if(left != null && right==null){return false;}if(left == null && right!=null){return false;}if(left.val != right.val){return false;}// 递归逻辑:继续比较左右两个子树的内外侧【相当于后序遍历,最后返回内侧和外侧的比较结果】boolean compareOutside = compare(left.left, right.right); boolean compareInside = compare(left.right, right.left);return compareInside && compareOutside; // 内外侧都是true的时候就返回true}} 解法二: 迭代法,用了单端队列
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isSymmetric(TreeNode root) {// 采用迭代法:用了单端队列Queue<TreeNode> myqueue = new LinkedList<>();myqueue.add(root.left);myqueue.add(root.right);while(!myqueue.isEmpty()){TreeNode leftnode = myqueue.poll();TreeNode rightnode = myqueue.poll();if(leftnode == null && rightnode == null){continue;}if(leftnode != null && rightnode == null){return false;}if(leftnode == null && rightnode != null){return false;}if(leftnode.val != rightnode.val){return false;}myqueue.add(leftnode.left);myqueue.add(rightnode.right);myqueue.add(leftnode.right);myqueue.add(rightnode.left);}return true;}
}
相关文章:

【递归】【后续遍历】【迭代】【队列】Leetcode 101 对称二叉树
【递归】【后续遍历】Leetcode 101 对称二叉树 解法一: 递归:后序遍历 左右中解法二: 迭代法,用了单端队列 ---------------🎈🎈对称二叉树 题目链接🎈🎈------------------- 解法一…...

Nginx https反向代理
接前一篇文章,今天看看https的反向代理怎么配置。 生成自签名证书和私钥 要使用https,首先需要有证书和私钥,这里创建一个测试用的自签名证书和私钥。 使用 openssl 命令生成服务器私钥文件 openssl genrsa -out server.key 2048生成证书…...

zip解压缩
使用unzip库可以轻松解压zip文件,源码下载地址:http://www.codeproject.com/Articles/7530/Zip-Utils-clean-elegant-simple-C-Win #include <Windows.h> #include"unzip.h" SetCurrentDirectory("c:\\"); HZIP hz OpenZip(…...

电动五金工具行业调研:政策促进市场发展
五金工具可以分为建筑五金、日用五金和家居五金等,科技的不断进步下五金工具产品也在逐渐创新进步。在国家一系列政策下五金工具行业更加规范化,使用也更加符合安全要求。 五金工具行业是指生产铁锤、螺丝刀、扳手、钳子、卷尺等小型工具的产业。这些工具…...

【矩阵】托普利茨矩阵
每日一道算法题之托普利茨矩阵 一、题目描述二、思路三、C代码 一、题目描述 题目来源:LeetCode 给你一个 m x n 的矩阵 a 。如果这个矩阵是托普利茨矩阵,返回 true ;否则,返回 false 。 如果矩阵上每一条由左上到右下的对角线上…...
DS:八大排序之归并排序、计数排序
创作不易,感谢三连支持!! 一、归并排序 1.1 思想 归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子…...
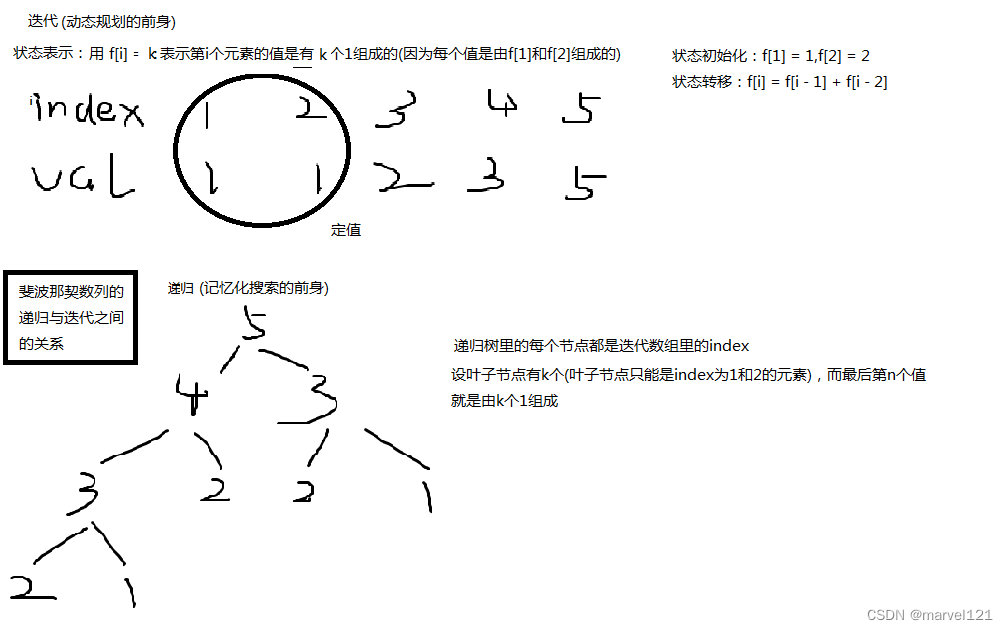
由斐波那契数列探究递推与递归
斐波那契数列定义: 斐波那契数列大家都非常熟悉。它的定义是: 对于给定的整数 x ,我们希望求出: f ( 1 ) f ( 2 ) … f ( x ) f(1)f(2)…f(x) f(1)f(2)…f(x) 的值。 有两种方法,分别是递推(迭代)与递归 具体解释如下图 备注…...

红队打靶练习:IMF: 1
目录 信息收集 1、arp 2、nmap 3、nikto 目录探测 gobuster dirsearch WEB 信息收集 get flag1 get flag2 get flag3 SQL注入 漏洞探测 脱库 get flag4 文件上传 反弹shell 提权 get flag5 get flag6 信息收集 1、arp ┌──(root㉿ru)-[~/kali] └─# a…...
?)
密码管理局以及什么是密评?为什么要做密评(商用密码应用安全性评估)?
文章目录 密码管理局以及什么是密评?为什么要做密评?关于密码管理局国家密码管理局属于什么级别?什么是密评?密评发展史为什么要做密评?目前密码应用的几个问题密评对象不做“密评”或密评不合格有什么影响?如何才能顺利通过密评?密评的相关标准参考密码管理局以及什么是…...
六、Datax通过json字符串运行
Datax通过json字符串运行 一、场景二、代码实现 一、场景 制作一个web应用,在页面上配置一个json字符串,保存在数据库里面。在执行json的时候,动态在本地创建一个json文件后执行,并识别是否成功,将执行过程保存在数据…...

关于数据库
目录 一 什么是数据库(DB) 二 什么是数据库管理系统(DBMS) 三 数据库的作用/好处 一 什么是数据库(DB) 简单理解,数据库是存放数据的地方,就像冰箱是存放冷鲜食品的地方。 数据是数据存储的基本对象,而数据分为多…...
洛谷C++简单题小练习day14—闰年推算小程序
day14--闰年推算小程序--2.18 习题概述 题目描述 输入 x,y,输出 [x,y] 区间中闰年个数,并在下一行输出所有闰年年份数字,使用空格隔开。 输入格式 输入两个正整数 x,y,以空格隔开。 输出格式 第一行输出一个正整数…...
房企关注的典型数字化场景之一:数字营销
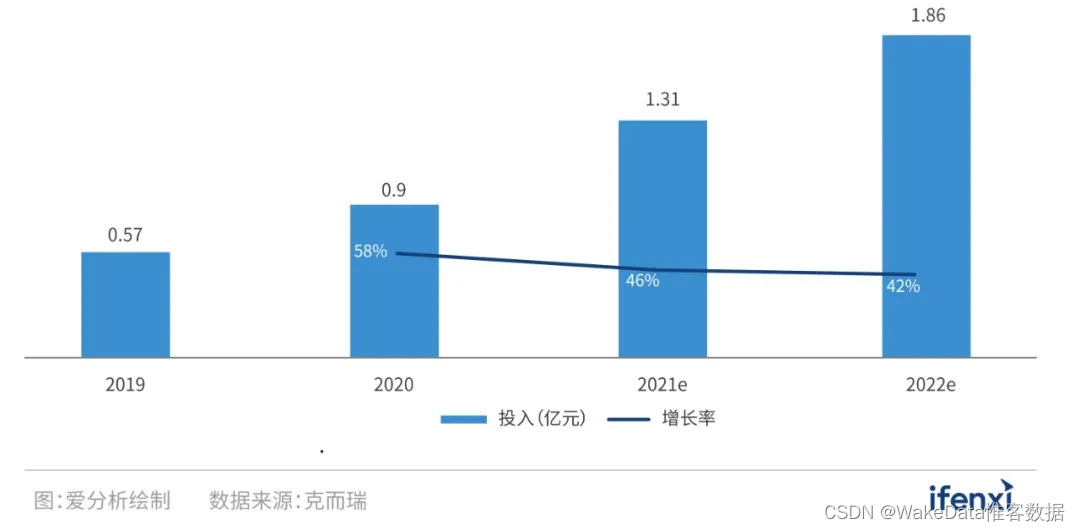
过去在增量时代下,房企的模式是“拿地-开发-卖房-拿地”,谁拿的地多、卖得快、利润高,谁“活得好”。而进入存量时代,加上政策调控影响,房企需要将核心竞争力转向精细化、多元化运营。 根据克而瑞数据统计,…...
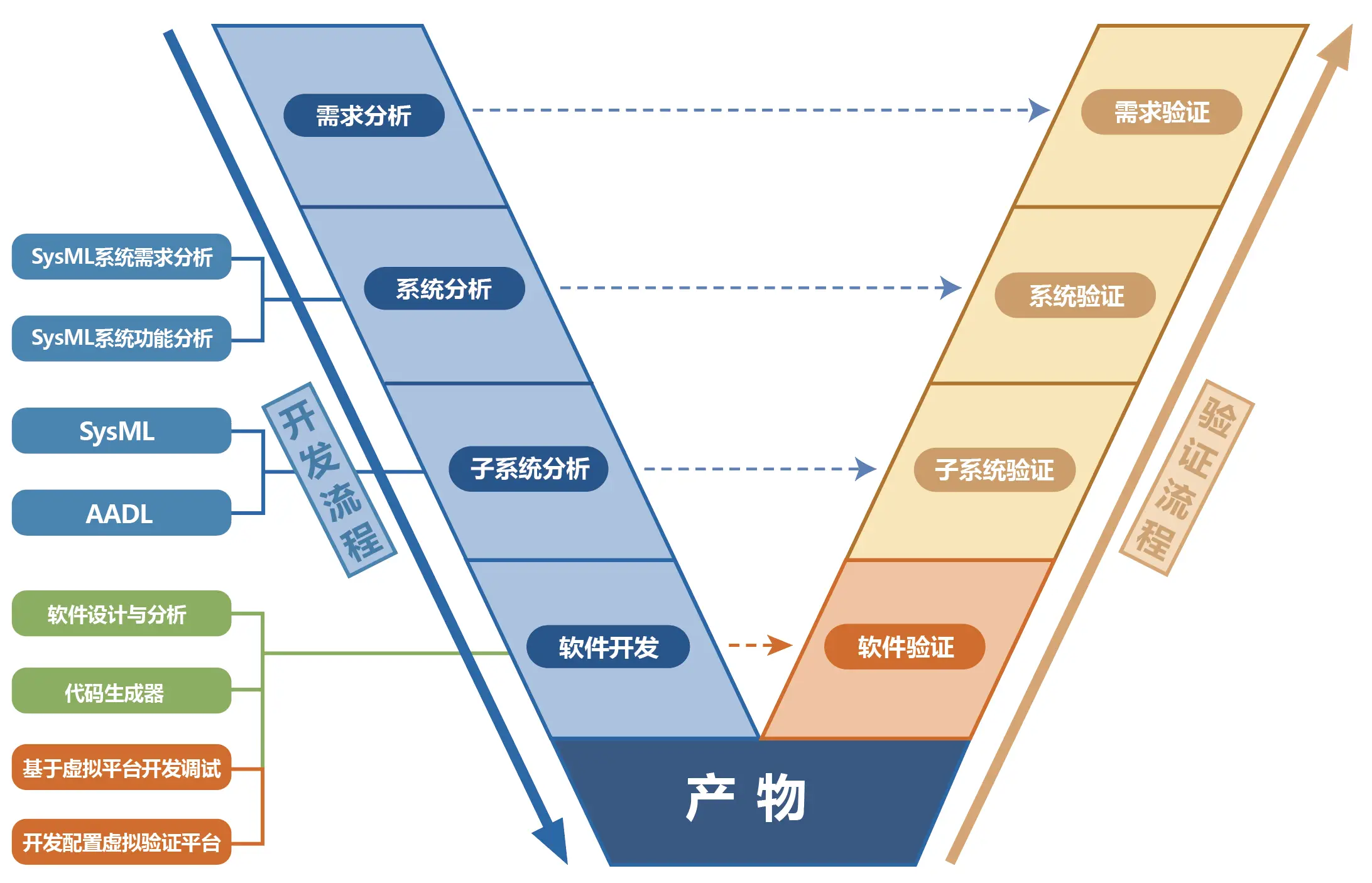
BMS再进阶(新能源汽车电池管理系统)
引言 一文入门BMS(电池管理系统)_bms电池管理-CSDN博客 BMS进阶(Type-C、PD快充、充电IC、SOC算法、电池管理IC)_充电ic asi aso功能-CSDN博客 本文是上面两篇博客的续篇,之前都是讲解一些BMS基本原理,…...

K8s Deployment挂载ConfigMap权限设置
目录 样例 1. 样例 …… volumes: - configMap:defaultMode: 420name: ${Existed_configmap_name} …… 其中“defaultMode: 420”是设置权限的 2. 解析 在K8s(Kubernetes)中,defaultMode是用来设置Configmap挂载后的文件权限࿰…...

百度智能云分布式数据库 GaiaDB-X 与龙芯平台完成兼容认证
近日,百度智能云的分布式关系型数据库软件 V3.0 与龙芯中科技术股份有限公司的龙芯 3C5000L/3C5000 处理器平台完成兼容性测试,功能与稳定性良好,获得了龙架构兼容互认证证书。 龙芯系列处理器 通用 CPU 处理器是信息产业的基础部件…...
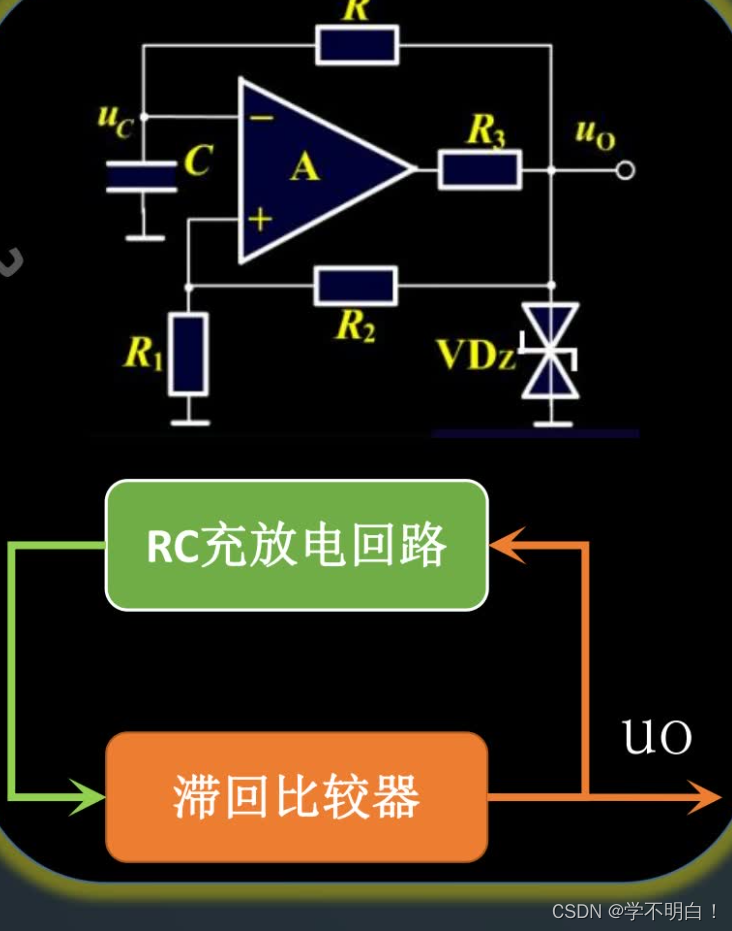
模拟电子技术——振荡器基本原理、RC桥式振荡器、矩形波发生电器
文章目录 前言一、振荡器什么是振荡器振荡器的基本电路结构振荡条件起振条件和稳幅原理 二、RC桥式振荡器什么是RC桥式振荡器RC串并联网络的选频特性振荡条件完整频率特性曲线举例 三、矩形波发生电器什么是矩形波发生电路稳态与暂态PWM脉宽调制矩形波发生电路基本组成 总结 前…...
Vue3+Vite+TS+Pinia+ElementPlus+Router+Axios创建项目
目录 初始项目组成1. 创建项目1.1 下载项目依赖1.2 项目自动启动1.3 src 别名设置vite.config.ts配置文件tsconfig.json配置若新创项目ts提示 1.4 运行测试 2. 清除默认样式2.1 样式清除代码下载2.2 src下创建公共样式文件夹style2.3 main.js中引入样式2.4 安装sass解析插件 2.…...

VMware虚拟机安装CentOS7
对于系统开发来说,开发者时常会需要涉及到不同的操作系统,比如Windows系统、Mac系统、Linux系统、Chrome OS系统、UNIX操作系统等。由于在同一台计算机上安装多个系统会占据我们大量的存储空间,所以虚拟机概念应运而生。本篇将介绍如何下载安…...
Avalonia学习(二十四)-系统界面
目前项目式练习,界面内容偏多,所以不给大家贴代码了,可以留言交流。此次为大家展示的是物联项目的例子,仅仅是学习,我把一些重点列举一下。 界面无边框 以前的样例主要是通过实现控件来完成的,前面已经有窗…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
