前端技巧之svg精灵图svg-sprite-loader
首先说明精灵图的必要性,其可以让我们只需要向服务器请求一次图片资源,就能加载很多图片,即能够减轻http请求造成的服务器压力。
然后这里要说明的是这个插件是webpack上面的,所以在vue2中比较好用,如果在vue3中,可能解决方案就不是这个插件了。
然后,svg的解决方案包含了精灵图和svg的全局组件配置,这里只是一部分,完整版的解决方案还有另一篇。
这是老师的图的细节。
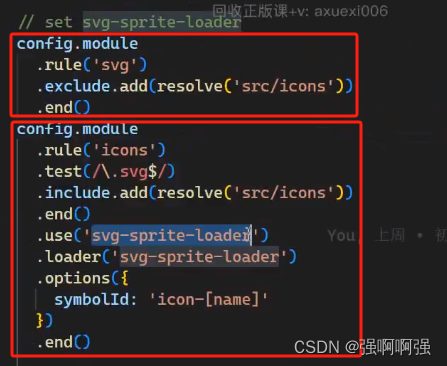
老师没提到上面的部分,然后这里还有我没注意到的细节就是,或许因为这个东西属于是webpack上的,所以在vue.config.js文件中并没有引入这个文件而是直接添加配置项即可。上面的框的意思是不要用默认的svg的方式来解析,下面的框意思是按照我们设置的svg-sprite-loader来将这些图片转成雪碧图。当然,我们想看到效果,可以通过检查浏览器的代码,找到
 这些代码。
这些代码。
相关文章:

前端技巧之svg精灵图svg-sprite-loader
首先说明精灵图的必要性,其可以让我们只需要向服务器请求一次图片资源,就能加载很多图片,即能够减轻http请求造成的服务器压力。 然后这里要说明的是这个插件是webpack上面的,所以在vue2中比较好用,如果在vue3中&…...

IO线程-day2
1> 使用fread和fwrite完成两个文件的拷贝 程序: #define MAXSIZE 1024 #include<myhead.h>int main(int argc, char const *argv[]) {FILE *srcfpNULL;FILE *destfpNULL;if(!(srcfpfopen("pm.bmp","r")))PRINT_ERR("");if…...
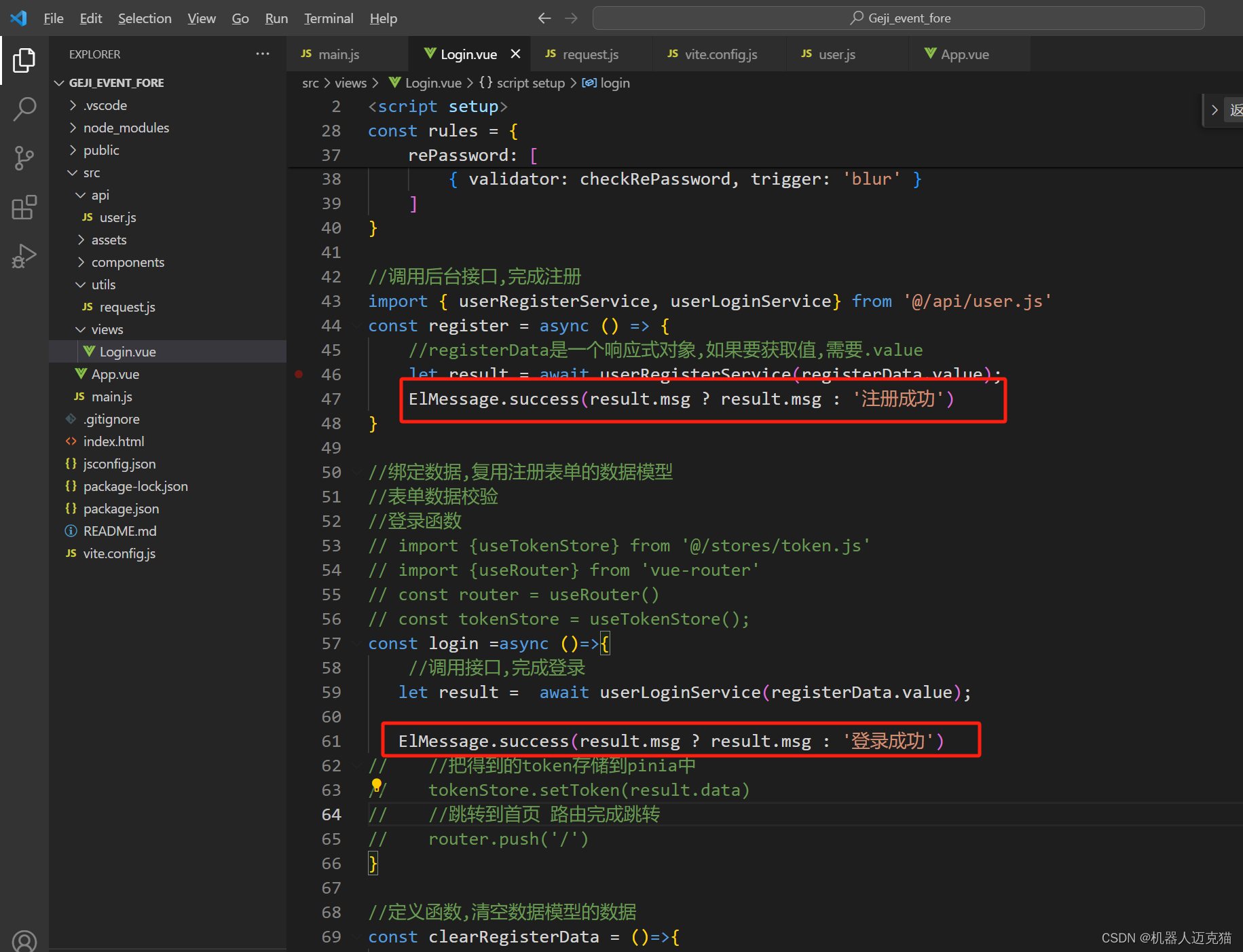
Spring Boot 笔记 024 登录页面
1.1 登录接口 //导入request.js请求工具 import request from /utils/request.js//提供调用注册接口的函数 export const userRegisterService (registerData)>{//借助于UrlSearchParams完成传递const params new URLSearchParams()for(let key in registerData){params.a…...

09_Java集合
一、Java集合框架概述 一方面, 面向对象语言对事物的体现都是以对象的形式,为了方便对多个对象的操作,就要对对象进行存储。另一方面,使用Array存储对象方面具有一些弊端,而Java 集合就像一种容器,可以动态…...

HCIA-HarmonyOS设备开发认证V2.0-3.2.轻量系统内核基础-软件定时器
目录 一、软件定时器基本概念二、软件定时器运行机制三、软件定时器状态四、软件定时器模式五、软件定时器开发流程六、软件定时器使用说明七、软件定时器接口八、代码分析(待续...)坚持就有收获 一、软件定时器基本概念 软件定时器,是基于系…...
考研证件照可以自己用手机拍吗?考研证件照p过可以通过审核吗?考研证件照有什么要求
一、考研证件照可以自己用手机拍吗 现在的智能手机相机技术先进,大多都配备了高像素摄像头,使得自拍照片的质量有了大幅提升。相较于传统的证件照拍摄,使用手机自拍考研证件照理论上是可行的。然而,考研证件照需要满足一定的规定…...
win10 环境下Python 3.8按装fastapi paddlepaddle 进行图片文字识别1
###按装 用conda 创建python 3.8的环境,可参看本人python下的其它文章。 在pycharm开发环境下按装相关的模块: pip install -i https://pypi.tuna.tsinghua.edu.cn/simple fastapi pip install -i https://pypi.tuna.tsinghua.edu.cn/simple "uvi…...

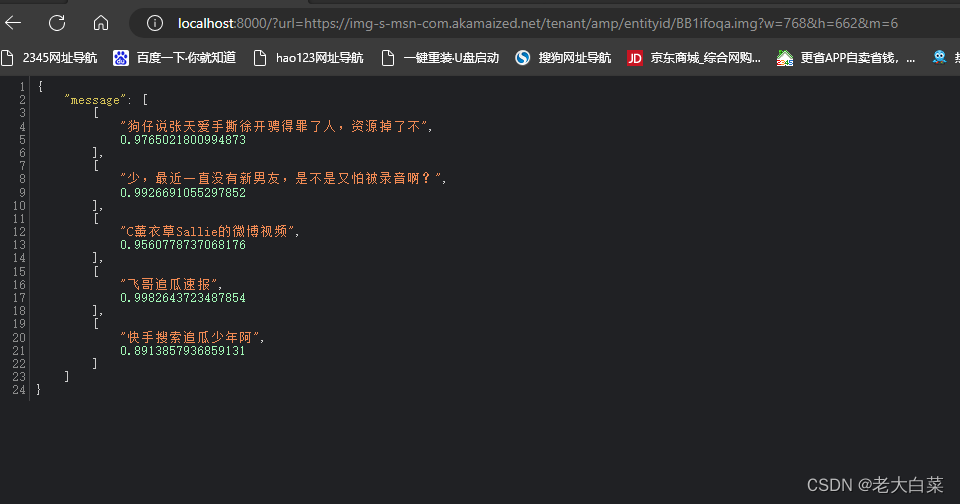
json字符串的处理
json字符串的处理 【1】解析json字符串(1)如果json格式字符串 ,最外层 是 中括号,表示数组,就使用方法(2)如果json格式字符串,最外层是 大括号,表示对象,就是…...

Java基础String常见的编程练习
1.对字符串数组进行排序 package javalianxi;import java.util.Arrays; import java.util.Comparator;public class Test1 {public static void main(String[] args) {String[] array { "cd", "CD", "bc", "AB", "ab", &q…...
| 491.递增子序列 46.全排列 47.全排列 II)
代码随想录算法训练营(回溯5)| 491.递增子序列 46.全排列 47.全排列 II
491.递增子序列 本题和大家刚做过的 90.子集II 非常像,但又很不一样,很容易掉坑里。 题目链接/文章讲解 视频讲解 46.全排列 本题重点感受一下,排列问题 与 组合问题,组合总和,子集问题的区别。 为什么排列问题不用…...

专业140+总分420+南京信息工程大学811信号与系统考研经验南信大电子信息与通信工程,真题,大纲,参考书
今年顺利被南信大电子信息录取,初试420,专业811信号与系统140(Jenny老师辅导班上140很多,真是大佬云集),今年应该是南信大电子信息最卷的一年,复试线比往年提高了很多,录取平均分380…...

一元函数微分学【高数笔记】
1. 什么是微分?什么是微商? 2. 什么是函数的微分? 3. 在函数的微分中,有什么样的关系? 4. 一元函数的微分运用在什么题型中? 5. 什么是一元函数?...
(16)Hive——企业调优经验
前言 本篇文章主要整理hive-3.1.2版本的企业调优经验,有误请指出~ 一、性能评估和优化 1.1 Explain查询计划 使用explain命令可以分析查询计划,查看计划中的资源消耗情况,定位潜在的性能问题,并进行相应的优化。 explain执行计划…...
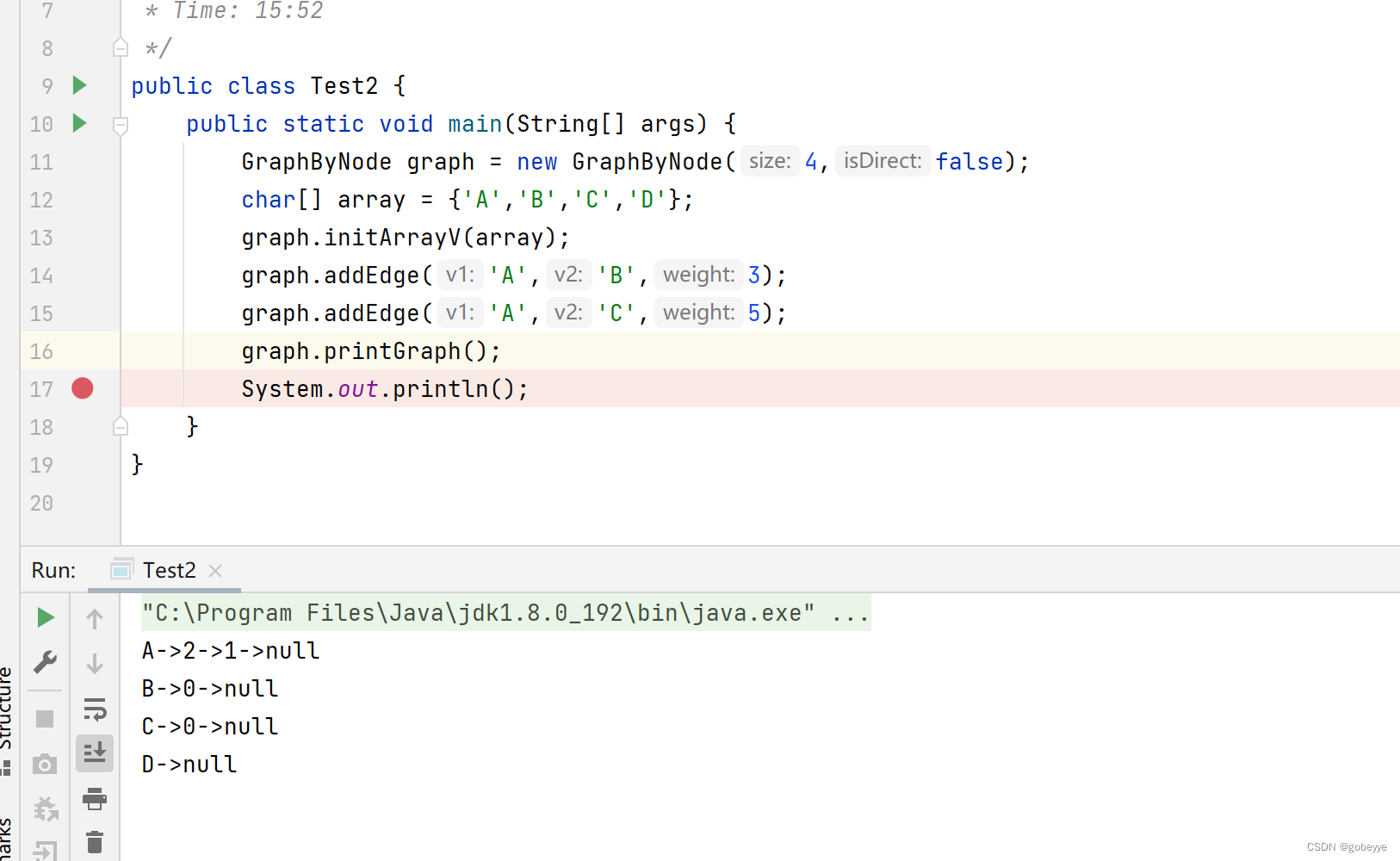
【详解】图的概念和存储结构(邻接矩阵,邻接表)
目录 图的基本概念: 图的存储结构 邻接矩阵(GraphByMatrix): 基本参数: 初始化: 获取顶点元素在其数组中的下标 : 添加边和权重: 获取顶点的度: 打印图…...

【AIGC】Stable Diffusion介绍
Stable Diffusion 是一个基于 OpenAI 的 Diffusion 模型的扩展版本,它采用了稳定扩散(Stable Diffusion)的技术,旨在提高图像生成和处理的质量。下面是 Stable Diffusion 的详细介绍: 基于 Diffusion 的图像生成&…...
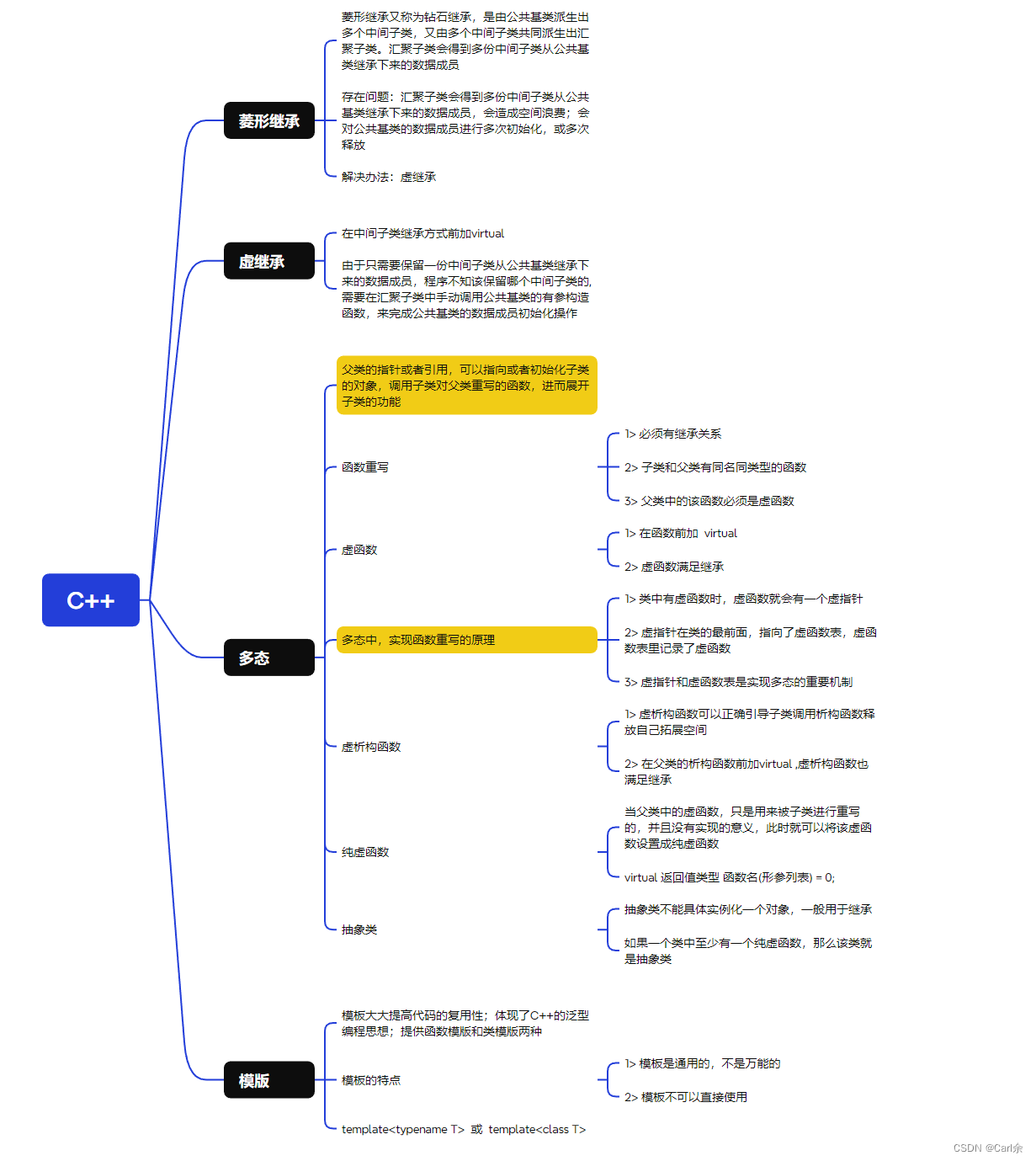
2024.2.18 C++QT 作业
思维导图 练习题 1>定义一个基类 Animal,其中有一个虛函数perform(),用于在子类中实现不同的表演行为。 #include <iostream>using namespace std;class Animal { public:virtual void perform() {cout << "这是一个动…...

【qt创建线程两种方式】
QT使用线程的两种方式 1.案例进度条 案例解析: 如图由组件一个进度条和三个按钮组成,当点击开始的时候进度条由0%到100%,点击暂停,进度条保持之前进度,再次点击暂停变为继续,点击停止按钮进度条停止。 案…...

网络安全-一句话木马
声明 遵纪守法 请严格遵守网络安全法相关条例! 此分享主要用于交流学习,请勿用于非法用途,一切后果自付。 一切未经授权的网络攻击均为违法行为,互联网非法外之地。 反制 大家在知道了常规一句话的木马之后,就可以通…...

在k8s中,使用DirectPV CSI作为分布式存储的优缺点
DirectPV 提供了一种直接将物理卷(Physical Volumes)与 Kubernetes 集群中的 Pod 绑定的机制。 利用 DirectPV,你可以将相应的 PV 直接与节点上的物理存储设备(如磁盘)进行绑定,而无需通过网络存储服务(如 NFS 或 Ceph)来提供存储。这种直接访问物理卷的方式,有助于提…...
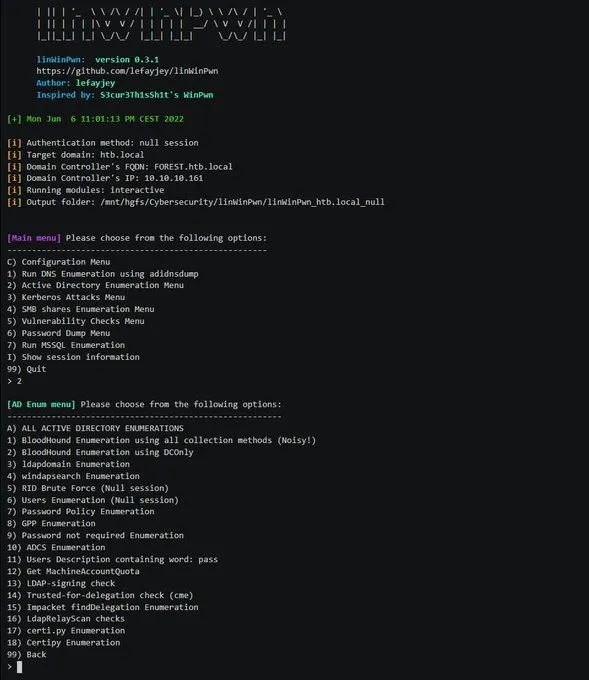
自动化AD域枚举和漏洞检测脚本
linWinPwn 是一个 bash 脚本,可自动执行许多 Active Directory 枚举和漏洞检查。该脚本基于很多现有工具实现其功能,其中包括:impacket、bloodhound、netexec、enum4linux-ng、ldapdomaindump、lsassy、smbmap、kerbrute、adidnsdump、certip…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

CVE-2023-25194源码分析与漏洞复现(Kafka JNDI注入)
漏洞概述 漏洞名称:Apache Kafka Connect JNDI注入导致的远程代码执行漏洞 CVE编号:CVE-2023-25194 CVSS评分:8.8 影响版本:Apache Kafka 2.3.0 - 3.3.2 修复版本:≥ 3.4.0 漏洞类型:反序列化导致的远程代…...
