题目 1138: C语言训练-求矩阵的两对角线上的元素之和
问题描述:
求矩阵的两对角线上的元素之和
样例输入:
3
1 2 3
4 5 6
7 8 9
样例输出:
25
问题分析:
因为奇数阶矩阵的主对角线和副对角线上的元素有重复,偶数阶矩阵的主对角线和副对角线上的元素无重复,需要分类讨论。
代码实现:
#include<stdio.h>
int main()
{int n;scanf("%d",&n);int a[n][n];int sum1=0,sum2=0,sum=0;for(int i=0;i<=n-1;i++){for(int j=0;j<=n-1;j++){scanf("%d",&a[i][j]);}}for(int i=0;i<n;i++){for(int j=i;j<=i;j++){sum1=sum1+a[i][j];}}for(int i=0;i<n;i++){for(int j=n-1-i;j>=n-i-1;j--){sum2=sum2+a[i][j]; }}if(n%2==0) {sum=sum1+sum2; }else{sum=sum1+sum2-a[n/2][n/2]; }printf("%d",sum);return 0;}
相关文章:

题目 1138: C语言训练-求矩阵的两对角线上的元素之和
问题描述: 求矩阵的两对角线上的元素之和 样例输入: 3 1 2 3 4 5 6 7 8 9 样例输出: 25 问题分析: 因为奇数阶矩阵的主对角线和副对角线上的元素有重复,偶数阶矩阵的主对角线和副对角线上的元素无重复&#x…...
第6讲自定义icon实现
自定义icon实现 component下新建SvgIcon目录,再新建index.vue 定义svg-icon组件 <template><svg class"svg-icon" aria-hidden"true"><use :xlink:href"iconName"></use></svg> </template>&…...

花费200元,我用全志H616和雪糕棒手搓了一台可UI交互的视觉循迹小车
常见的视觉循迹小车都具备有路径识别、轨迹跟踪、转向避障、自主决策等基本功能,如果不采用红外避障的方案,那么想要完全满足以上这些功能,摄像头、电机、传感器这类关键部件缺一不可,由此一来小车成本也就难以控制了。 但如果&a…...

AUTOSAR OS TASK
什么是TASK? 我们在裸机中跑代码,程序永远只能单活动流水执行,当程序需要等待的时候,CPU就一直在waiting状态,无法高效的利用CPU,这个时候就引入了并发运行需求。一个系统能同时执行多个不同活动的系统叫做并发系统。其中这个系统中的每个并发执行的活动都由TASK(任务)…...
陇剑杯 2021刷题记录
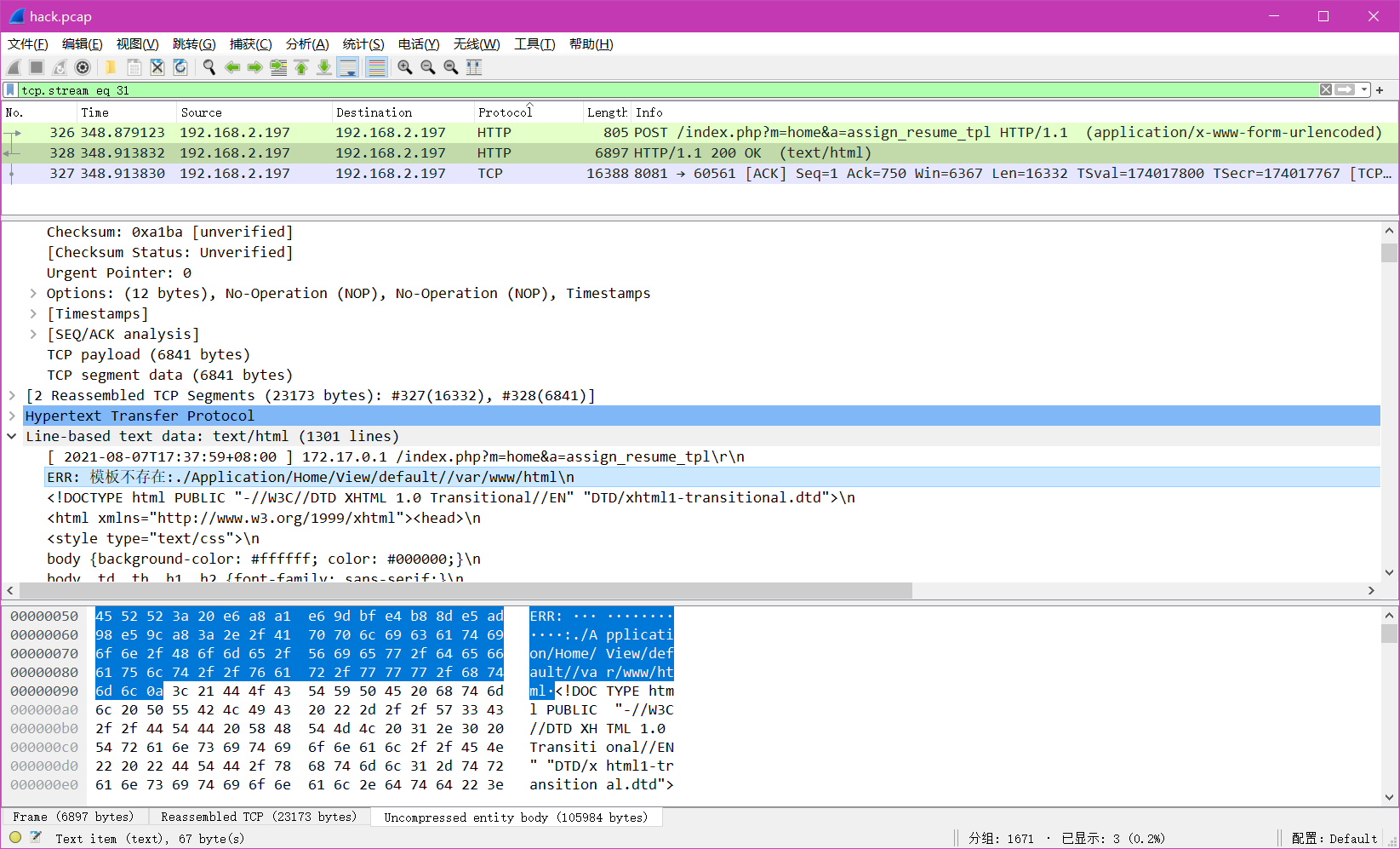
题目位置:https://www.nssctf.cn/上有 陇剑杯 2021 1. 签到题题目描述分析答案小结 2. jwt问1析1答案小结 问2析2答案小结 问3析3答案 问4析4答案 问5析5答案 问6析6答案 3. webshell问1析1答案 问2析2答案 问3析3答案 1. 签到题 题目描述 此时正在进行的可能是_…...
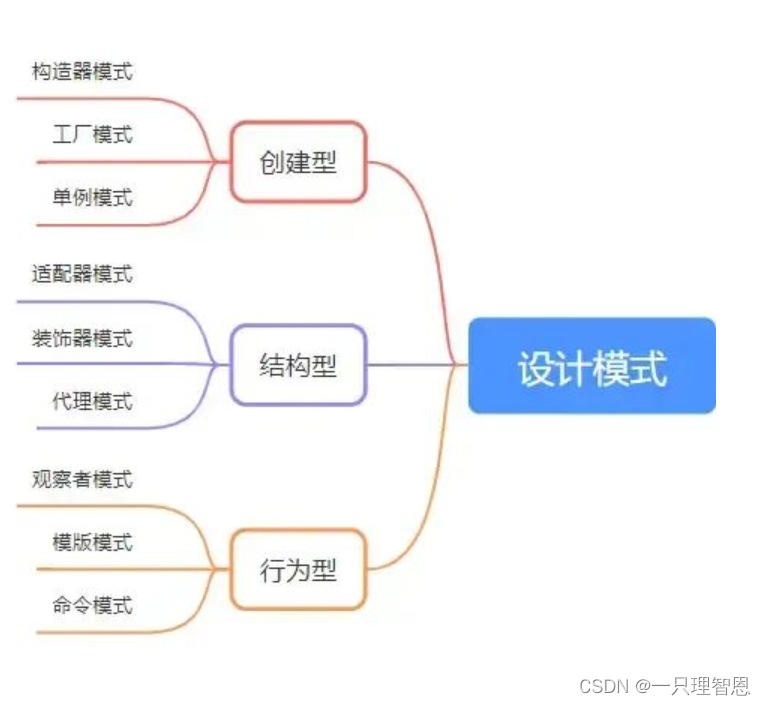
前端常见的设计模式
说到设计模式,大家想到的就是六大原则,23种模式。这么多模式,并非都要记住,但作为前端开发,对于前端出现率高的设计模式还是有必要了解并掌握的,浅浅掌握9种模式后,整理了这份文章。 六大原则&…...
OpenAI视频生成模型Sora的全面解析:从ViViT、扩散Transformer到NaViT、VideoPoet
前言 真没想到,距离视频生成上一轮的集中爆发(详见《Sora之前的视频生成发展史:从Gen2、Emu Video到PixelDance、SVD、Pika 1.0》)才过去三个月,没想OpenAI一出手,该领域又直接变天了 自打2.16日OpenAI发布sora以来(其开发团队包…...

3个密码学相关的问题
一、离散对数问题(Discrete Logarithm Problem, DLP) 问题描述:给定 有限阿贝尓群 G中的2个元素a和b,找出最小的正整数x满足:b a ^^ x (或者证明这样的x不存在)。 二、阶数问题(O…...

5G网络eMBB、uRLLC、mMTC
ITU(国际电信联盟)于2015年9月正式定义了5G的三大应用场景:eMBB(增强型移动宽带)、uRLLC(低时延高可靠通信)、mMTC(海量物联网通信)。 eMBB是4G MBB(移动宽带…...
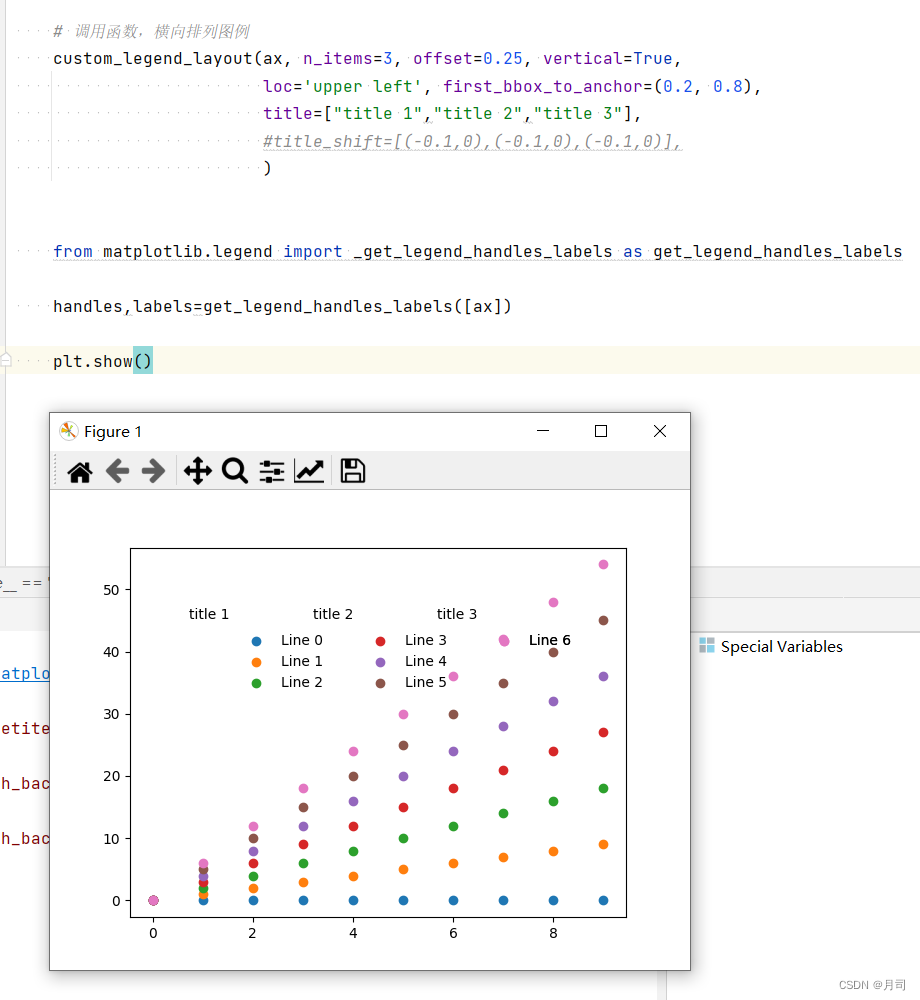
matplotlib图例使用案例1.1:在不同行或列的图例上添加title
我们将图例进行行显示或者列显示后,只能想继续赋予不同行或者列不同的title来进行分类。比较简单的方式,就是通过ax.annotate方法添加标签,这样方法复用率比较低,每次使用都要微调ax.annotate的显示位置。比较方便的方法是在案例1…...

nginx 日志改为json格式
nginx 日志改为json格式 场景描述效果变更旧样式新样式 场景描述 正常使用nginx时,使用默认的日志输出格式,对于后续日志接入其他第三方日志收集、清洗环节,因分隔符问题可能不是很友好。 xxxx - - [19/Feb/2024:11:16:48 0800] "GET …...
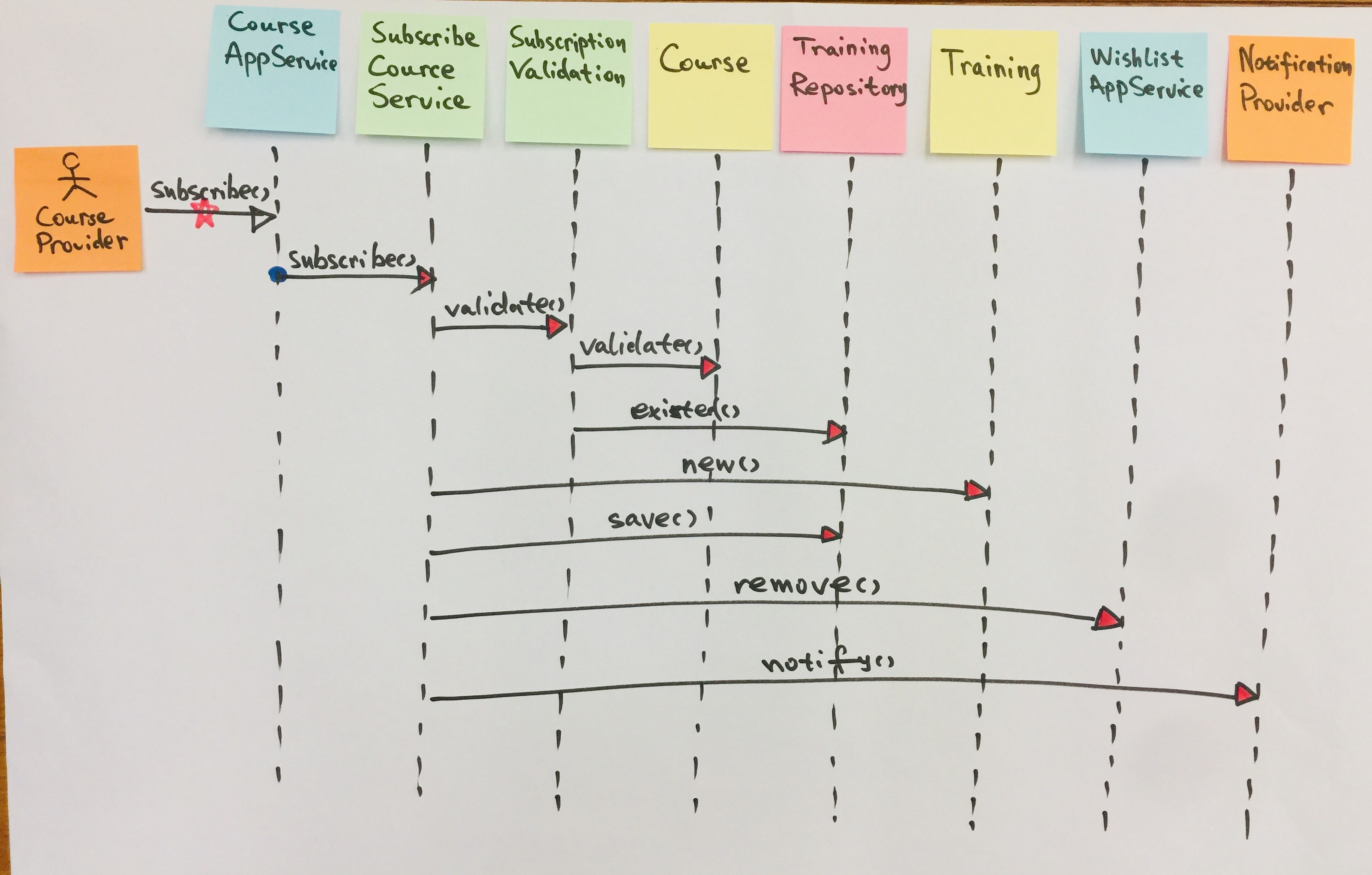
【DDD】学习笔记-应用服务
Eric Evans 为运用领域驱动设计的系统架构划定了层次,在领域层和展现层之间引入了应用层(Application Layer):“应用层要尽量简单,不包含业务规则或者知识,而只为下一层(指领域层)中…...
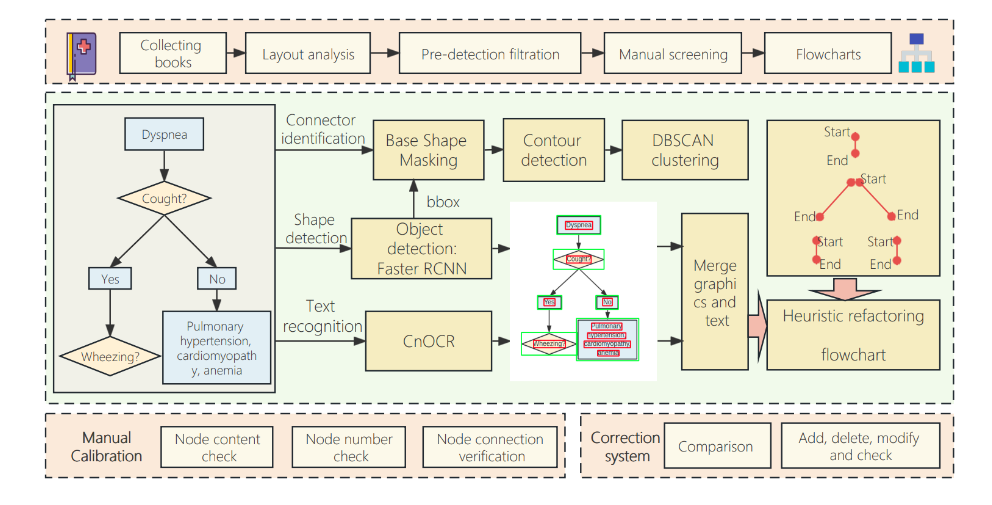
【医学大模型】MEDDM LLM-Executable CGT 结构化医学知识: 将临床指导树结构化,便于LLM理解和应用
MEDDM LLM-Executable CGT 结构化医学知识: 将临床指导树结构化,便于LLM理解和应用 提出背景对比传统医学大模型流程步骤临床指导树流程图识别临床决策支持系统 总结解决方案设计数据收集与处理系统实施临床决策支持 提出背景 论文:https://arxiv.org/p…...

YOLOV8改进系列指南
基于Ultralytics的YOLOV8改进项目.(69.9) 为了感谢各位对V8项目的支持,本项目的赠品是yolov5-PAGCP通道剪枝算法.具体使用教程 专栏改进汇总 二次创新系列 ultralytics/cfg/models/v8/yolov8-RevCol.yaml 使用(ICLR2023)Reversible Column Networks对yolov8主干进行重设计,里…...

FlinkSql一个简单的测试程序
FlinkSql一个简单的测试程序 以下是一个简单的 Flink SQL 示例,展示了如何使用 Flink Table API 和 Flink SQL 进行基本的数据流处理。 定义数据实体 CC : - CC 类表示数据流中的元素,包含两个字段: character (字符&a…...

二、ActiveMQ安装
ActiveMQ安装 一、相关环境二、安装Java8三、下载安装包四、启动五、其他命令六、开放端口七、后台管理 一、相关环境 环境:Centos7.9安装ActiveMQ版本:5.15.9JDK8 二、安装Java8 安装教程:https://qingsi.blog.csdn.net/article/details/…...

通俗易懂的L0范数和L1范数及其Python实现
定义 L0 范数(L0-Norm) L0 范数并不是真正意义上的一个范数,因为它不满足范数的三角不等式性质,但它在数学优化和信号处理等领域有着实际的应用。L0 范数指的是向量中非零元素的个数。它通常用来度量向量的稀疏性。数学上表示为…...

如何在30天内使用python制作一个卡牌游戏
如何在30天内使用python制作一个卡牌游戏 第1-5天:规划和设计第6-10天:搭建游戏框架第11-20天:核心游戏机制开发第21-25天:游戏界面和用户体验第26-30天:测试和发布附加建议游戏类型游戏规则设计界面设计技术选型第6-…...

VsCode指定插件安装目录
VsCode指定插件安装目录 VsCode安装的默认目录是在用户目录(%HomePath%)下的.vscode文件夹下的extensions目录下,随着安装插件越来越多会占用大量C盘空间。 指定VsCode的插件目录 Vscode安装目录: D:\Microsoft VS Code\Code.exeVscode插件安装目录&a…...
解决npm淘宝镜像到期问题
1 背景 由于node安装插件是从国外服务器下载,如果没有“特殊手法”,就可能会遇到下载速度慢、或其它异常问题。 所以如果npm的服务器在中国就好了,于是我们乐于分享的淘宝团队干了这事。你可以用此只读的淘宝服务代替官方版本,且…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
