动态DP入门线性动态DP
动态DP入门&线性动态DP
- 前言
- 核心思想
- 例1
- 例2
- 2024牛客寒假4K
- 2022牛客寒假2J
- 结论
前言
OI-WiKi上有一个动态DP讲解,直接讲到了树型DP领域,同时需要树链剖分,门槛有点高。本文针对线性DP做一个动态DP的讲解。
首先当然要懂得一定的DP的相关知识,然后需要知道DP方程的矩阵表达。可以看这里——根据递推公式构造系数矩阵用于快速幂。很多DP的状态转移方程都可以写成矩阵形式,由此就有了矩阵快速幂优化和动态DP的基础。特别是本文专门举例的线性DP。
核心思想
常规的DP方程一般形如:
D i = f ( D i − 1 ) D_i=f(D_{i-1}) Di=f(Di−1)
即 D i D_i Di是 D i − 1 D_{i-1} Di−1的某个函数。与矩阵快速幂优化类似,想办法将DP方程改为:
[ D i 0 或 1 ] = M i × [ D i − 1 0 或 1 ] \begin{bmatrix} D_i \\ 0或1 \end{bmatrix}=M_i\times\begin{bmatrix} D_{i-1} \\ 0或1 \end{bmatrix} [Di0或1]=Mi×[Di−10或1]
其中 M i M_i Mi表示 i i i位置的系数矩阵。这里用到了矩阵乘法,不过不一定是乘法,只是类乘操作而已,即满足某种性质的操作。令上述包含 D i D_i Di的向量记为 X i X_i Xi,则方程改为
X i = ∏ j = 1 i M j × X 0 X_i=\prod_{j=1}^{i}{M_j}\times{X_0} Xi=j=1∏iMj×X0
于是求 X i X_i Xi转化为区间矩阵求积的操作,这个区间操作可以使用线段树维护。同时很自然的也就支持了修改操作。
例1
首先看一个完全不需要动态DP的例子。给定一个数组,单点修改,区间求和。
规划方程: D i = A i + D i − 1 D_i=A_{i}+D_{i-1} Di=Ai+Di−1
写成矩阵形式:
[ D i 1 ] = [ 1 A i 0 1 ] × [ D i − 1 1 ] \begin{bmatrix} D_i \\ 1 \end{bmatrix}=\begin{bmatrix} 1 & A_i \\ 0 & 1 \end{bmatrix}\times\begin{bmatrix} D_{i-1} \\ 1 \end{bmatrix} [Di1]=[10Ai1]×[Di−11]
因此第 i i i个系数矩阵就是
[ 1 A i 0 1 ] \begin{bmatrix} 1 & A_i \\ 0 & 1 \end{bmatrix} [10Ai1]
而且此处用的就是正常的矩阵乘法。用线段树可以轻松维护其区间积与单点修改操作(修改某个点 A i A_i Ai,就是修改第 i i i个系数矩阵)。对于区间查询 [ l , r ] [l,r] [l,r],只需要计算:
a n s = ( ∏ i = l r [ 1 A i 0 1 ] ) × [ 0 1 ] ans=\big(\prod_{i=l}^{r}\begin{bmatrix} 1 & A_i \\ 0 & 1 \end{bmatrix}\big)\times\begin{bmatrix} 0 \\ 1 \end{bmatrix} ans=(i=l∏r[10Ai1])×[01]
即可, a n s [ 1 ] ans[1] ans[1]即答案。
当然,如果进一步推敲的话,可以发现这个线段树本质上就是维护的 A i A_i Ai的和。这是一个实现上毫无必要的、但很好的仅供学习的例子,如果后面的例子有难度的话。
例2
再看一个复杂一点点的例子。给定一个数组,查询区间最大子段和,单点修改。首先这个问题仍然可以直接使用线段树解决。其次,来看看动态DP的做法。
令 U i U_i Ui是以 i i i结尾的最大子段和, V i V_i Vi是 [ 1 , i ] [1,i] [1,i]区间的最大子段和,则规划方程是:
U i = max ( A i , A i + U i − 1 ) V i = max ( U i , V i − 1 ) U_i=\max{(A_i,A_{i}+U_{i-1})} \\ V_i=\max{(U_i, V_{i-1})} Ui=max(Ai,Ai+Ui−1)Vi=max(Ui,Vi−1)
首先修改其中一个DP方程为: V i = max ( A i , A i + U i − 1 , V i − 1 ) V_i=\max{(A_i,A_{i}+U_{i-1},V_{i-1})} Vi=max(Ai,Ai+Ui−1,Vi−1)
然后写成矩阵形式:
[ U i V i 0 ] = [ A i − ∞ A i A i 0 A i − ∞ − ∞ 0 ] × [ U i − 1 V i − 1 0 ] \begin{bmatrix} U_i \\ V_i \\ 0 \end{bmatrix}=\begin{bmatrix} A_i & -\infty & A_i \\ A_i & 0 & A_i \\ -\infty & -\infty & 0 \end{bmatrix}\times\begin{bmatrix} U_{i-1} \\ V_{i-1} \\ 0 \end{bmatrix} UiVi0 = AiAi−∞−∞0−∞AiAi0 × Ui−1Vi−10
这里的 × \times ×表示矩阵的类乘操作或者说是矩阵的广义乘法操作,定义如下:令矩阵 C = A × B C=A\times{B} C=A×B,则
C i , j = max k = 1 3 ( A i , k + B k , j ) C_{i,j}=\max_{k=1}^{3}{(A_{i,k}+B_{k,j})} Ci,j=k=1max3(Ai,k+Bk,j)
写成单行、单列的形式即:
[ a 1 a 2 a 3 ] × [ b 1 b 2 b 3 ] = max ( a 1 + b 1 , a 2 + b 2 , a 3 + b 3 ) \begin{bmatrix}a_1 & a_2 & a_3\end{bmatrix}\times\begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix}=\max{(a_1+b_1,a_2+b_2,a_3+b_3)} [a1a2a3]× b1b2b3 =max(a1+b1,a2+b2,a3+b3)
因此
[ A i − ∞ A i A i 0 A i − ∞ − ∞ 0 ] \begin{bmatrix} A_i & -\infty & A_i \\ A_i & 0 & A_i \\ -\infty & -\infty & 0 \end{bmatrix} AiAi−∞−∞0−∞AiAi0
就是第 i i i个矩阵,一共要维护 N N N个矩阵。修改操作也很容易维护,改变 A i A_i Ai就是改变第 i i i个矩阵。区间查询操作 [ l , r ] [l,r] [l,r],就是计算:
a n s = ( ∏ i = l r [ A i − ∞ A i A i 0 A i − ∞ − ∞ 0 ] ) × [ − ∞ − ∞ 0 ] ans=\big(\prod_{i=l}^{r}\begin{bmatrix} A_i & -\infty & A_i \\ A_i & 0 & A_i \\ -\infty & -\infty & 0 \end{bmatrix}\big)\times\begin{bmatrix} -\infty \\ -\infty \\ 0 \end{bmatrix} ans=(i=l∏r AiAi−∞−∞0−∞AiAi0 )× −∞−∞0
a n s [ 1 ] ans[1] ans[1]就是答案,因为 a n s [ 1 ] ans[1] ans[1]对应了规划目标 V V V。
2024牛客寒假4K
同样,这个题目可以不用动态DP,直接用线段树维护相关信息即可。
题目大意:给定一个字符串仅包含
YBR,表示命令。初始位于0位置且右边无边界限制。命令执行如下:
Y指令表示在当前位置添加一个块;B指令表示先右移一格到达一个新位置,再在这个新位置添加一个块;R指令表示先将当前位置的块倍增一下,再添加一个块(假设当前位置本来有3块,则该指令过后变成7块)。还有 Q Q Q个操作,一共分两类:
- p c: 将第p个位置的命令改为c;
- s e: 从零开始,依次执行 [ s , e ] [s,e] [s,e]区间的命令,问最后的块数。
对每个操作2,输出答案。
令 D i D_i Di是第 i i i个操作后当前位置的块数(注意,不一定是第 i i i个位置,因为一个命令不一定新增一个位置,不过这个并没有影响)。令 S i S_i Si是第 i i i个操作后总块数。令动态规划的列向量是:
[ D i S i 1 ] \begin{bmatrix} D_{i} \\ S_{i} \\ 1 \end{bmatrix} DiSi1 简单推理一下就可以得到YBR三个命令分别对应的三个系数矩阵是:
[ 1 0 1 0 1 1 0 0 1 ] , [ 0 0 1 0 1 1 0 0 1 ] , [ 2 0 1 1 1 1 0 0 1 ] \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{bmatrix}, \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{bmatrix}, \begin{bmatrix} 2 & 0 & 1 \\ 1 & 1 & 1 \\ 0 & 0 & 1 \end{bmatrix} 100010111 , 000010111 , 210010111
因此可以得到一个矩阵的数组,维护这个矩阵数组的区间积就行,支持单点修改。这里用到的就是正经的矩阵乘法。当然这里会注意到系数矩阵连乘展开以后,其实是倒序的。前面的两个例子之所以没有这个问题,是因为例1中的矩阵形式比较特殊,因此支持乘法的交换律。而例2中的操作本身就支持交换律。所以那个两个例子都可以直接按顺序维护。这个例子则是正经的矩阵乘法,不支持交换律。因此倒过来维护即可。
2022牛客寒假2J
题目大意:有三种魔法球、十种技能,每种技能都是三种魔法球的组合(可重复)。现在需要连续释放技能,但是手中只能持有三个魔法球,且必须按照队列性质。
例如需要连续释放技能1和2,则首先持有三个魔法球,记作
a1 a2 a3
释放技能1。随后,如果a1a2a3不是技能2的组合,则必须先拿掉a1, 追加a4(可以自由选择追加的魔法球)。
此时手中持有变为了:a2a3a4
如果能满足施法,即可完成。
否则必须扔掉a2,追加a5。
还不行的话就扔掉a3,追加a6。此时必然可以释放技能2。手中持有必须按顺序,但是技能构成无需按顺序。
例如假设输入给定技能1的构成是a3a2a1,则手中持有a1a2a3一样可以释放技能1现在给定N个技能的序列,两种操作:
- s e: 问连续释放[s, e]区间内的技能,最少需要依次拿几个魔法球,每次施法之初手中都是空的
- p x: 将第p个位置的技能修改为x
首先释放第一个技能必须拿3个球,然后考虑后续。
从技能a到技能b,需要追加的球的数量显然与a魔法球以及b魔法球的排列有关。
一个技能最多可能存在6种不同的排列。
因此令 D i , j , u , v D_{i,j,u,v} Di,j,u,v 记录技能 i i i的排列 u u u后面跟技能 j j j的排列 v v v时需要改变的魔法球的数量。
所以D是一个 10 × 10 × 6 × 6 10\times10\times6\times6 10×10×6×6的四维数组,可以预处理出来。
再考虑一段连续的释放,首先考虑 [ 1... n ] [1...n] [1...n],令 Z n u Z_{nu} Znu表示从1释放到 n n n的最少数量,且以 n n n的 u u u排列结尾。
则:
Z n u = min { Z n − 1 , v + D n − 1 , n , v , u , v 是 n − 1 的所有排列状态 } Z_{nu} = \min\{Z_{n-1,v} + D_{n-1,n,v,u}, v是n-1的所有排列状态\} Znu=min{Zn−1,v+Dn−1,n,v,u,v是n−1的所有排列状态}
则 min { Z n u , u 是 n 的所有排列 } \min\{Z_{nu}, u是n的所有排列\} min{Znu,u是n的所有排列}为所求。
将 Z n Z_n Zn看作是列向量,将 D i j D_{ij} Dij看做是矩阵,可以将规划方程写成矩阵形式
Z n = D n − 1 , n × Z n − 1 Z_n = D_{n-1,n}\times{Z_{n - 1}} Zn=Dn−1,n×Zn−1
同样,这里是用的是类乘操作,与例2中类似,只不过这里取的是最小值。同时注意到这个操作是支持交换律的,因此按正序维护即可。
题目给定了 N N N个技能,则一共需要 N − 1 N-1 N−1次转换,因此维护 N − 1 N-1 N−1个矩阵即可。
结论
感觉上线性动态DP是不需要的,因为似乎可以直接设计线段树,维护相关信息完成。不过从线性DP入手动态DP,不失为一个好的学习路线。另一方面,动态DP可以提供一个统一的模板,构思简单,实现高度一致,在常数时间充足的情况下,值得一试。
相关文章:

动态DP入门线性动态DP
动态DP入门&线性动态DP 前言核心思想例1例22024牛客寒假4K2022牛客寒假2J结论 前言 OI-WiKi上有一个动态DP讲解,直接讲到了树型DP领域,同时需要树链剖分,门槛有点高。本文针对线性DP做一个动态DP的讲解。 首先当然要懂得一定的DP的相关…...

基于python+django+vue.js开发的停车管理系统
功能介绍 平台采用B/S结构,后端采用主流的Python语言进行开发,前端采用主流的Vue.js进行开发。 功能包括:车位管理、会员管理、停车场管理、违规管理、用户管理、日志管理、系统信息模块。 源码地址 https://github.com/geeeeeeeek/pytho…...

网站管理新利器:免费在线生成 robots.txt 文件!
🤖 探索网站管理新利器:免费在线生成 robots.txt 文件! 你是否曾为搜索引擎爬虫而烦恼?现在,我们推出全新的在线 robots.txt 文件生成工具,让你轻松管理网站爬虫访问权限,提升网站的可搜索性和…...
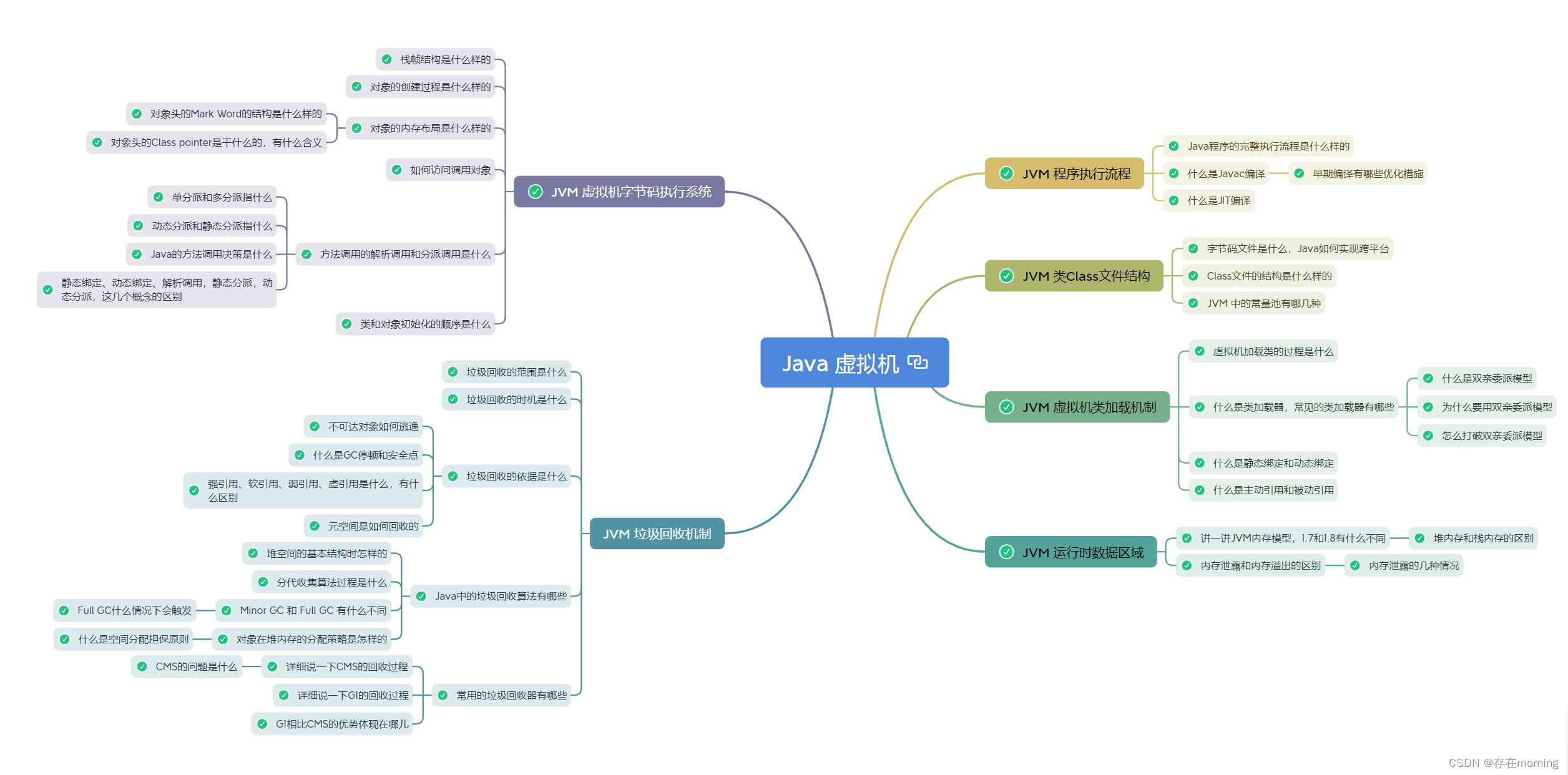
【Java程序员面试专栏 Java领域】Java虚拟机 核心面试指引
关于Java 虚拟机部分的核心知识进行一网打尽,主要包括Java虚拟机的内存分区,执行流程等,通过一篇文章串联面试重点,并且帮助加强日常基础知识的理解,全局思维导图如下所示 JVM 程序执行流程 包括Java程序的完整执行流程,以及Javac编译,JIT即时编译 Java程序的完整执…...

洛谷C++简单题小练习day15—计算阶乘小程序(不用循环)
day15--计算阶乘小程序--2.19 习题概述 题目描述 求 n!,也就是 123⋯n。 挑战:尝试不使用循环语句(for、while)完成这个任务。 输入格式 第一行输入一个正整数 n。 输出格式 输出一个正整数,表示 n! 代码部分 …...

Vue报错,xxx is defined #变量未定义
vue.js:5129 [Vue warn]: Error in v-on handler: "ReferenceError: count is not defined" 浏览器将这个变量 当做全局变量了,事实上它只是实例中的变量 加上this指定,是vue实例中的变量...
Idea启动Gradle报错: Please, re-import the Gradle project and try again
Idea启动Gradle报错:Warning:Unable to make the module: reading, related gradle configuration was not found. Please, re-import the Gradle project and try again. 解决办法: 开启步骤:View -> Tool Windows -> Gradle 点击refe…...

Python函数(一)
目录 一、定义函数 (一)向函数传递信息 (二)实参和形参 二、传递实参 (一)位置实参 (二)关键字实参 (三)默认值 (四)等效的函…...

Excel表的内容批量生成个人加水印的Word文档
Excel表的内容批量生成个人加水印的Word文档 以下代码可以直接复制到docm文件里使用 Sub 宏1()Dim MyDialog As FileDialogDim GetStr As String, Adoc As StringDim PsDoc As DocumentApplication.ScreenUpdating FalseSet MyDialog Application.FileDialog(msoFileDialogF…...

微服务设计:Spring Cloud API 网关概述
Spring Cloud API 网关是指一个位于微服务架构中的代理服务器,它负责将外部请求路由到内部微服务。API 网关可以提供多种功能,包括: 路由: 将请求路由到特定的微服务。负载均衡: 将请求分散到多个微服务实例上。安全: 身份验证、授权和安全策…...
stm32学习笔记-STLINK使用
stm32学习笔记-STLINK使用 使用ST-LINK调试程序进度表格 使用ST-LINK调试程序 说明 组成 总结 记录使用STLINK进行项目的烧写和调试,旨在高效的进行代码调试学习工具包括笔记本、keil5MDK、stm32f030c8t6电表主机、STLINK V2、导线、电表代码总的来说࿰…...

Linux CentOS stream 9 firewalld
随着互联网行业快速发展,服务器成为用户部署网络业务重要的网络工具,但随之而来的就是更密集的网络攻击,这给网站带来了很大的阻碍。防火墙作为保障网络安全的主要设备,可以很好的抵御网络攻击。 防火墙基本上使用硬件和软件两种…...
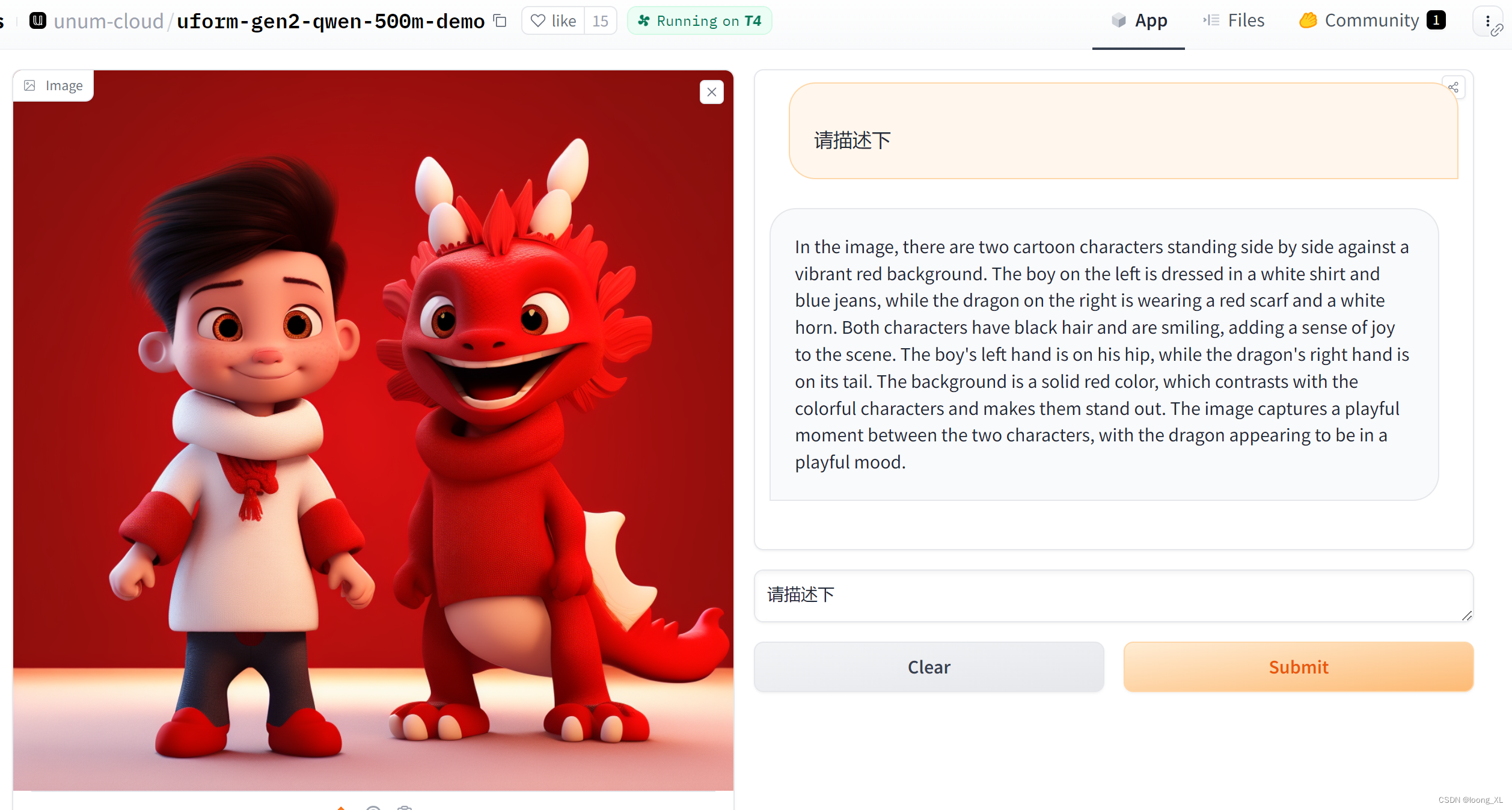
VLM多模态图像识别小模型UForm
参考:https://github.com/unum-cloud/uform https://huggingface.co/unum-cloud/uform-gen2-qwen-500m https://baijiahao.baidu.com/s?id=1787054120353641459&wfr=spider&for=pc demo:https://huggingface.co/spaces/unum-cloud/uform-gen2-qwen-500m-demo UF…...
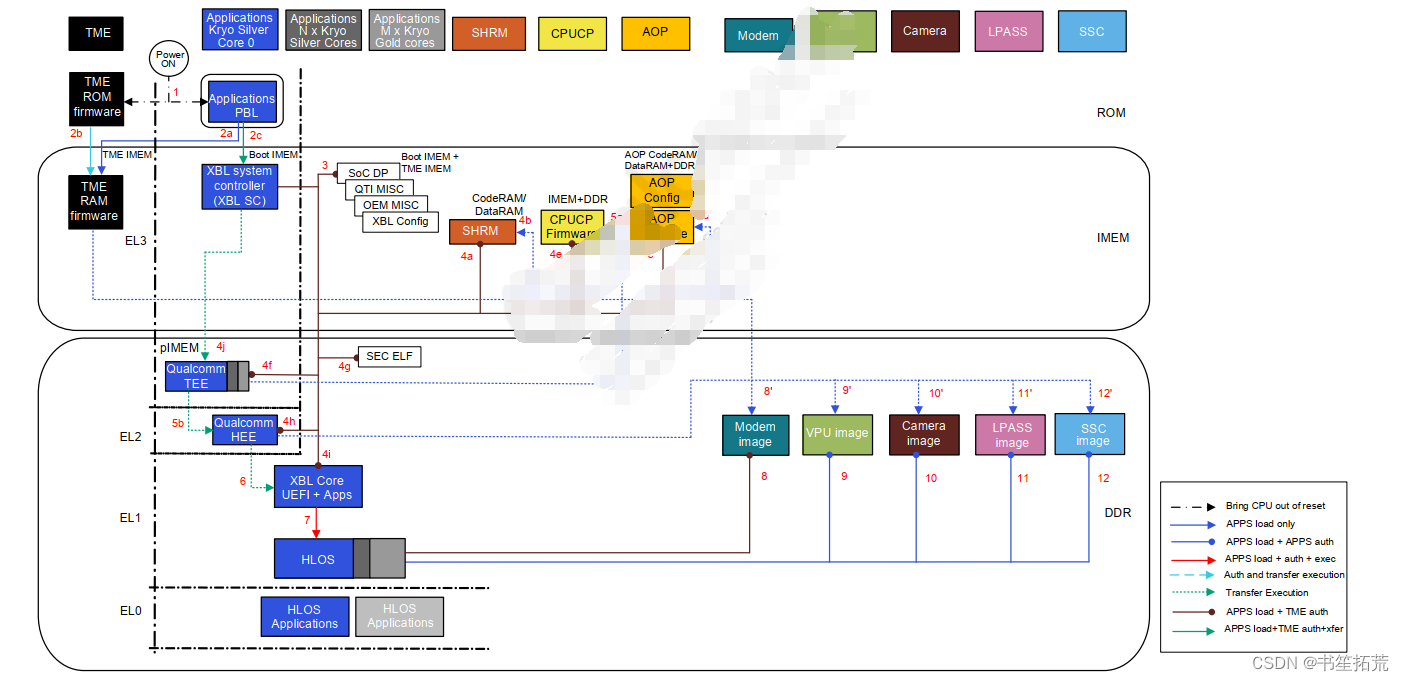
我的NPI项目之设备系统启动(七) -- 高通OS启动阶段和镜像分区简析
每当有新的平台起来的时候,大概率会伴随着新系统的发布,无论是高通的还是Google Andorid的。在做平台Bringup阶段总会遇到各种各样的专业术语。例如,总是会听到有人说PBL,SBL,XBL,UFEI,Bootload…...
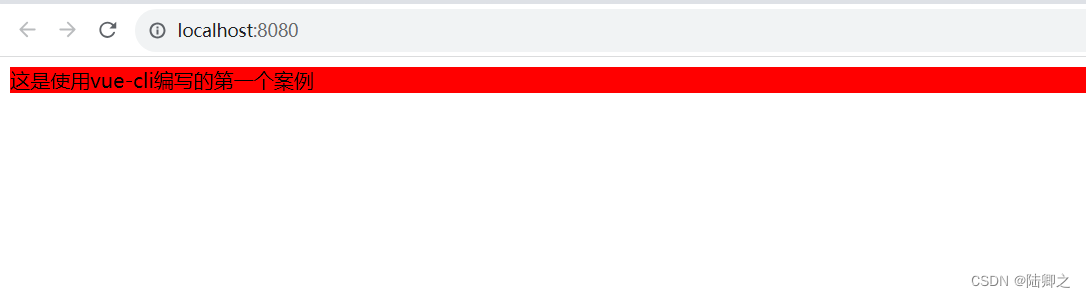
vue框架-vue-cli
vue-cli Vue CLI是一个官方的脚手架工具,用于快速搭建基于Vue.js的项目。Vue CLI提供了一整套可配置的脚手架,可以帮助开发人员快速构建现代化的Web应用程序。 Vue CLI通过提供预先配置好的Webpack模板和插件,使得开发人员可以在不需要手动编写Webpack配置的情况下快速创建…...

Sora (text-to-video model-文本转视频模型)
以下翻译自维基百科 Introduction Sora 是由美国人工智能 (AI) 研究组织 OpenAI 开发的文本到视频模型。它可以根据描述性提示生成视频,并及时向前或向后扩展现有视频。截至 2024 年 2 月,它尚未发布,尚未向公众开放。 History 在 Sora 之…...
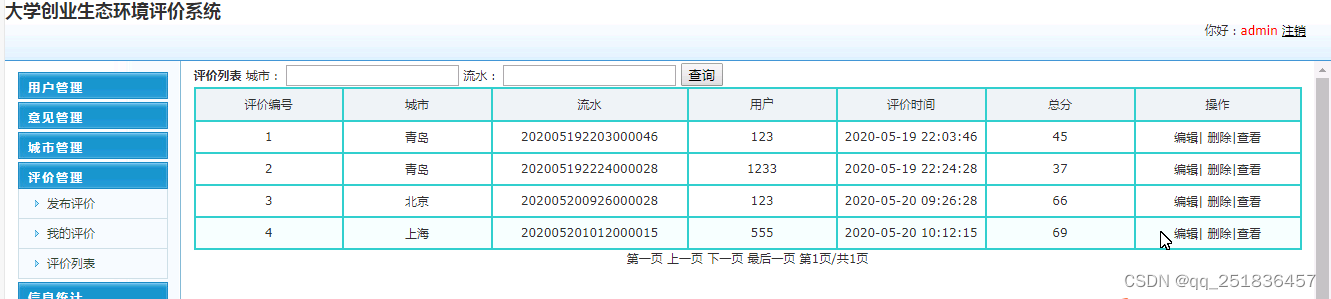
java生态环境评价Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 java 生态环境评价管理系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为 TOMCAT7.0,Myeclipse8.5开发,数据库为Mysq…...
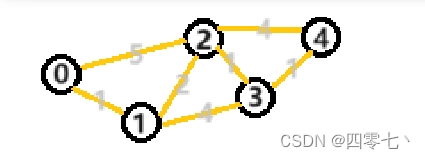
数据结构-最短路径(Dijkstra算法与Floyd算法)
介绍 对于网图来说,最短路径是指两顶点之间经过的边上权值之和最少的路径,其路径上第一个点记为源点,最后一个为终点。 计算最短路径有两个经典算法,即迪杰斯特拉(Dijkstra)算法与弗洛伊德(Fl…...

文献速递:GAN医学影像合成--联邦生成对抗网络基础医学图像合成中的后门攻击与防御
文献速递:GAN医学影像合成–联邦生成对抗网络基础医学图像合成中的后门攻击与防御 01 文献速递介绍 虽然深度学习在医疗保健研究中产生了显著影响,但其在医疗保健领域的影响无疑比在其他应用领域更慢、更有限。造成这种情况的一个重要原因是ÿ…...
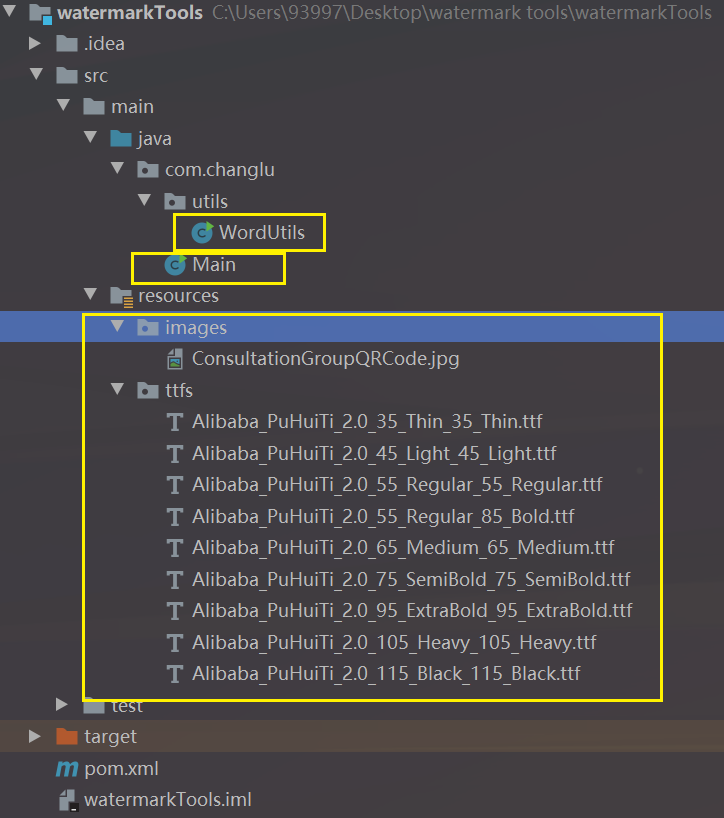
Java实现自动化pdf打水印小项目 使用技术pdfbox、Documents4j
文章目录 前言源码获取一、需求说明二、 调研pdf处理工具word处理工具 三、技术栈选择四、功能实现实现效果详细功能介绍详细代码实现项目目录WordUtilsMain类实现部分:第一部分Main类实现部分:第二部分Main类实现部分:第三部分 资料获取 前言…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...
