python coding with ChatGPT 打卡第20天| 二叉搜索树:搜索、验证、最小绝对差、众数
相关推荐
python coding with ChatGPT 打卡第12天| 二叉树:理论基础
python coding with ChatGPT 打卡第13天| 二叉树的深度优先遍历
python coding with ChatGPT 打卡第14天| 二叉树的广度优先遍历
python coding with ChatGPT 打卡第15天| 二叉树:翻转二叉树、对称二叉树
python coding with ChatGPT 打卡第16天| 二叉树:完全二叉树、平衡二叉树、二叉树的所有路径、左叶子之和
python coding with ChatGPT 打卡第17天| 二叉树:找树左下角的值、路径总和
python coding with ChatGPT 打卡第18天| 二叉树:从中序与后序遍历序列构造二叉树、最大二叉树
python coding with ChatGPT 打卡第19天| 二叉树:合并二叉树
二叉搜索树中的搜索
Key Points
1.二叉搜索树是一个有序树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉搜索树
2.二叉搜索树的迭代
一提到二叉树遍历的迭代法,可能立刻想起使用栈来模拟深度遍历,使用队列来模拟广度遍历。
对于二叉搜索树可就不一样了,因为二叉搜索树的特殊性,也就是节点的有序性,可以不使用辅助栈或者队列就可以写出迭代法。
对于一般二叉树,递归过程中还有回溯的过程,例如走一个左方向的分支走到头了,那么要调头,在走右分支。
而对于二叉搜索树,不需要回溯的过程,因为节点的有序性就帮我们确定了搜索的方向。
相关题目
700. 二叉搜索树中的搜索
视频讲解
这次搜索有方向了
重点分析
方法一:
递归法
def searchBST(root, val):if not root:return Noneif root.val > val:return searchBST(root.left, val)if root.val < val:return searchBST(root.right, val)return root
方法二:
迭代法
def searchBST(root, val):current = rootwhile current:if current.val > val:current = current.leftcontinueif current.val < val:current = current.rightcontinueelse:breakreturn current
验证二叉搜索树
Key Points
在中序遍历下,输出的二叉搜索树节点的数值是升序序列。
相关题目
98. 验证二叉搜索树
视频讲解
你对二叉搜索树的了解还不够
重点分析
方法一:
不使用有序序列

我们可以定义一个辅助函数checkBST,它接收四个参数:当前节点node、minVal(当前节点值允许的最小值)、maxVal(当前节点值允许的最大值)、以及初始的根节点root。这个辅助函数将帮助我们递归地验证每个子树,同时保持跟踪允许的值的范围。
def checkBST(node, minVal, maxVal):if not node:return Trueif node.val <= minVal or node.val >= maxVal:return Falsereturn checkBST(node.left, minVal, node.val) and checkBST(node.right, node.val, maxVal)def isValidBST(root):return checkBST(root, float('-inf'), float('inf'))
这段代码使用了一个嵌套的辅助函数checkBST来递归地验证每个节点是否符合二叉搜索树的条件,它通过维护每个节点的值允许的最小值和最大值来实现。这种方法能够确保所有的左子树节点都小于它的父节点,并且所有的右子树节点都大于它的父节点,同时还考虑了所有祖先节点的约束条件。
方法二:
使用有序序列 + 双指针 递归法

class Solution:def __init__(self):self.pre = None # 用来记录前一个节点def isValidBST(self, root):if root is None:return Trueleft = self.isValidBST(root.left)if self.pre is not None and self.pre.val >= root.val:return Falseself.pre = root # 记录前一个节点right = self.isValidBST(root.right)return left and right方法三:
使用有序序列 + 双指针 迭代法

def isValidBST(root):stack = []prev = Nonewhile stack or root:# 遍历到最左while root:stack.append(root)root = root.left# 访问节点root = stack.pop()# 检查当前节点是否大于前一个节点if prev and root.val <= prev.val:return Falseprev = root# 转向右子树root = root.rightreturn True
二叉搜索树的最小绝对差
Key Points
- 在升序数组中,任意两个相邻元素的差值最小
- 1)暴力法:先中序遍历得到升序数列,再遍历数组求最小差值;
2)简化法:遍历的过程中使用双指针
相关题目
530. 二叉搜索树的最小绝对差
视频讲解
二叉搜索树中的双指针遍历
重点分析
方法一:
递归法
class Solution(object):def __init__(self):self.pre = None self.diff = float('inf') # 只使用一次,所以是全局变量def getMinimumDifference(self, root):self.in_traversal(root)return self.diffdef in_traversal(self, root):if not root:returnself.in_traversal(root.left)if self.pre:self.diff = min(root.val - self.pre.val, self.diff)self.pre = rootself.in_traversal(root.right)return
方法二:
迭代法 + 暴力
def getMinimumDifference(root):stack_record = []current = rootres = []while stack_record or current:while current:stack_record.append(current)current = current.leftcurrent = stack_record.pop()res.append(current.val)# 左中都处理完了,转向右current = current.righti = 0j = i+1diff = res[j] - res[i]while j < len(res):diff = min(res[j] - res[i], diff)i += 1j += 1return diff
注:LeetCode题目中说明节点至少为两个,所以使用双指针不用讨论数组长度
方法三:
迭代法+简化
def getMinimumDifference(root):stack_record = []current = rootdiff = float('inf')pre = Nonewhile stack_record or current:while current:stack_record.append(current)current = current.leftcurrent = stack_record.pop()if pre is None: # if not pre 不行,警惕0的情况pre = current.valelse:diff = min(current.val-pre, diff)pre = current.valcurrent = current.rightreturn diff二叉搜索树中的众数
Key Points
首先如果不是二叉搜索树的话,应该怎么解题,是二叉搜索树,又应该如何解题,两种方式做一个比较,可以加深大家对二叉树的理解。
- 如果不是二叉搜索树,最直观的方法一定是把这个树都遍历了,用map统计频率,把频率排个序,最后取前面高频的元素的集合。
- 对于二叉搜索树,遍历有序数组的元素出现频率,从头遍历,那么一定是相邻两个元素作比较,然后就把出现频率最高的元素输出就可以了。
相关题目
501. 二叉搜索树中的众数
视频讲解
双指针+代码技巧
重点分析
方法一:
暴力法 哈希表(迭代)
def findMode(root):res = []stack_record = []current = rootwhile stack_record or current:while current:stack_record.append(current)current = current.leftcurrent = stack_record.pop()res.append(current.val)current = current.rightrecord = {}for x in res:record[x] = record.get(x, 0) + 1record_sort = sorted(record.items(), key=lambda x:x[1], reverse=True)results = []max_val = record_sort[0][1]for x in record_sort:if x[1] == max_val:results.append(x[0])else:breakreturn results
方法二:
遍历两遍 双指针 (迭代法)
def findMode(root):res = []stack_record = []current = rootwhile stack_record or current:while current:stack_record.append(current)current = current.leftcurrent = stack_record.pop()res.append(current.val)current = current.rightpre = Nonecount = 0max_count = 0results = []for x in res:if pre is not None:if pre == x:count +=1else:count = 1else:count = 1pre = xif count == max_count:results.append(x)elif count > max_count:max_count = countresults = [x]return results
方法三:
遍历一遍 迭代法
def findMode(root):res = []pre = Nonemax_count = 0count = 0stack_record = []current = rootwhile stack_record or current:while current:stack_record.append(current)current = current.leftcurrent = stack_record.pop()if pre:if current.val == pre.val:count += 1else:count = 1else:count = 1pre = currentif count == max_count:res.append(current.val)elif count > max_count:max_count = countres = [current.val]current = current.rightreturn res
方法四:
遍历一遍 递归法
class Solution:def __init__(self):self.pre = Noneself.res = []self.max_count = 0self.count = 0def in_traversal(self, root):if not root:returnself.in_traversal(root.left)if self.pre:if root.val == self.pre.val:self.count += 1else:self.count = 1else:self.count = 1self.pre = rootif self.count == self.max_count:self.res.append(root.val)elif self.count > self.max_count:self.max_count = self.countself.res = [root.val]self.in_traversal(root.right)returndef findMode(self, root):self.in_traversal(root)return self.res
相关文章:

python coding with ChatGPT 打卡第20天| 二叉搜索树:搜索、验证、最小绝对差、众数
相关推荐 python coding with ChatGPT 打卡第12天| 二叉树:理论基础 python coding with ChatGPT 打卡第13天| 二叉树的深度优先遍历 python coding with ChatGPT 打卡第14天| 二叉树的广度优先遍历 python coding with ChatGPT 打卡第15天| 二叉树:翻转…...

Stable Diffusion——基础模型、VAE、LORA、Embedding各个模型的介绍与使用方法
前言 Stable Diffusion(稳定扩散)是一种生成模型,基于扩散过程来生成高质量的图像。它通过一个渐进过程,从一个简单的噪声开始,逐步转变成目标图像,生成高保真度的图像。这个模型的基础版本是基于扩散过程…...

Python自动化部署与配置管理:Ansible与Docker
Ansible 和 Docker 是两种常用于自动化部署和配置管理的工具。Ansible 是一个基于 Python 的自动化运维工具,可以配置管理、应用部署、任务自动化等。而 Docker 是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的容器中&…...

《摔跤吧爸爸》19岁女星突患皮肌炎离世
从确诊到离世仅10天……罕见病“皮肌炎”! 曾凭借在知名电影《摔跤吧!爸爸》中饰演童年时期“小芭比塔”一角而广受喜爱的年轻演员苏哈尼巴特纳格尔不幸离世,年仅19岁。她的突然逝世引发了全球关注,据苏哈妮的家人表示࿰…...

用结构体数组,完成宠物信息登记管理。
管理宠物的名字,品种,年龄。 实现功能如下: 1.插入宠物信息 2.遍历宠物信息 #include <stdio.h> #define N 100 typedef struct chongwu { char name[20]; char pingz[10]; int age; }cw; void intset_cw(cw *ptr,int *pnum) { printf("请…...

频率主义线性回归和贝叶斯线性回归
整体概述 频率主义(Frequentist)线性回归和贝叶斯(Bayesian)线性回归是统计学中用于数据分析和预测的两种主要方法,特别是在建模关于因变量和自变量之间线性关系的上下文中。尽管两种方法都用于线性回归分析ÿ…...
)
【感知算法】Dempster-Shafer理论(下)
尝试DS理论应用到自动驾驶地图众包更新。 地图特征变化判断 a mass function is applied to quantify the evidence of the existence. existence state: existenct、non-existent、tenative、conflict ∃ ∄ Ω ϕ \exist \\ \not\exist \\ \Omega \\ \phi ∃∃Ωϕ ma…...

通过conda安装cudatoolikit和cudnn
通过conda安装cudatoolikit和cudnn 安装cudatoolkit安装cudnn安装cudatoolkit-dev 安装cudatoolkit conda install cudatoolkit11.3 -c https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/ 安装cudnn conda install cudnn8.5 -c https://mirrors.tuna.tsinghua.edu.…...

vue中使用jsx语法
请注意,在 Vue 中使用 JSX 时,你仍然需要通过 h 函数(通常是一个别名,对应于 createElement 函数)来创建虚拟 DOM 元素。在下面的例子中,h 函数作为 render 函数的参数传入,但在 JSX 语法中你通…...
我的NPI项目之Android USB 系列(一) - 遥望和USB的相识
和USB应该是老朋友了,从2011年接触Android开发开始,就天天和USB打交道了。那时候还有不 对称扁头的usb/方口的usb,直到如今使用广泛的防反插USB3.0 type-C。 但是,一直有一个不是很清楚的问题萦绕在心头,那就是。先有…...
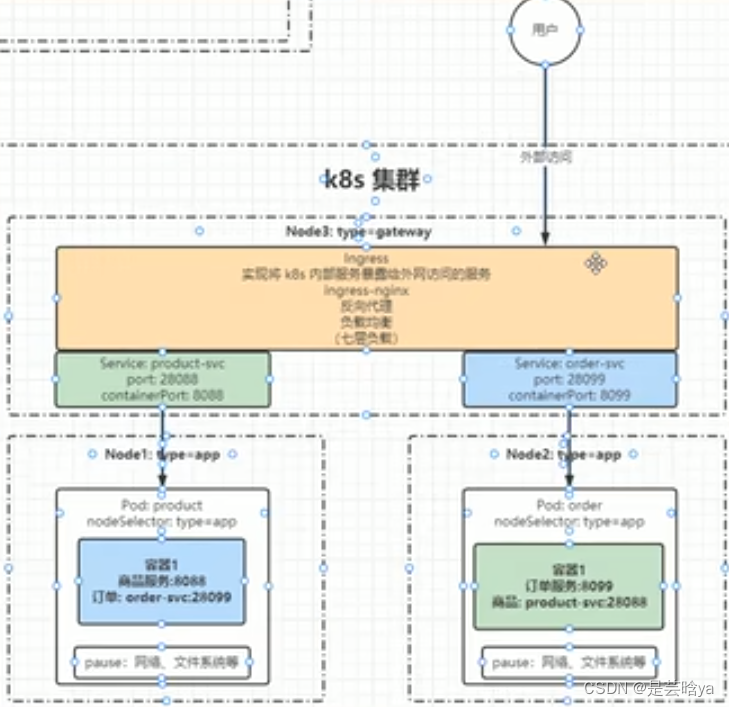
K8s进阶之路-命名空间级-服务发现 :
服务发现: Service(东西流量):集群内网络通信、负载均衡(四层负载)内部跨节点,节点与节点之间的通信,以及pod与pod之间的通信,用Service暴露端口即可实现 Ingress&#…...

智慧公厕管理系统:让城市智慧驿站更加智慧舒适
智慧公厕管理系统是城市智慧驿站中不可或缺的一部分,它通过全方位的信息化解决方案,为公共厕所的使用、运营和管理提供了一种智能化的方式。作为城市智慧驿站的重要组成部分,智慧公厕管理系统发挥着重要的作用,为城市社会民生提供…...
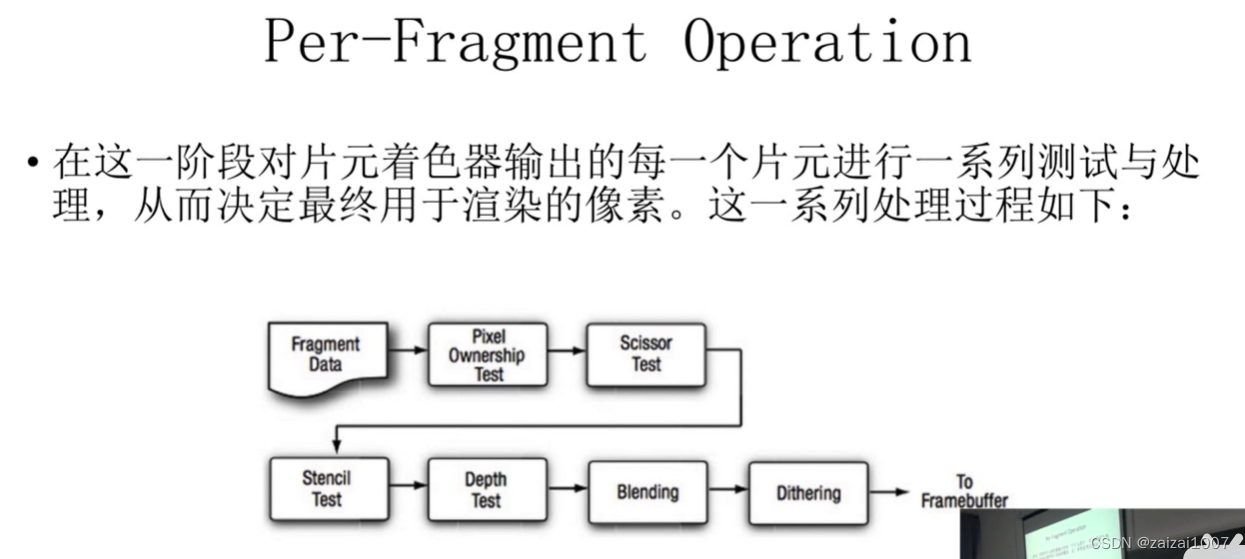
图形渲染基础学习
原文链接:游戏开发入门(三)图形渲染_如果一个面只有三个像素进行渲染可以理解为是定点渲染吗?-CSDN博客 游戏开发入门(三)图形渲染笔记: 渲染一般分为离线渲染与实时渲染,游戏中我们用的都是…...

每日学习总结20240219
每日总结 20240219 1.文件类型.csv CSV文件是一种以逗号分隔值(Comma-Separated Values)为标记的文本文件,它可以用来存储表格数据。每一行表示一条记录,而每一条记录中的字段则使用逗号或其他特定的分隔符进行分隔。 常用场景…...

K8s进阶之路-安装部署K8s
参考:(部署过程参考的下面红色字体文档链接就可以,步骤很详细,重点部分在下面做了标注) 安装部署K8S集群文档: 使用kubeadm方式搭建K8S集群 GitBook 本机: master:10.0.0.13 maste…...
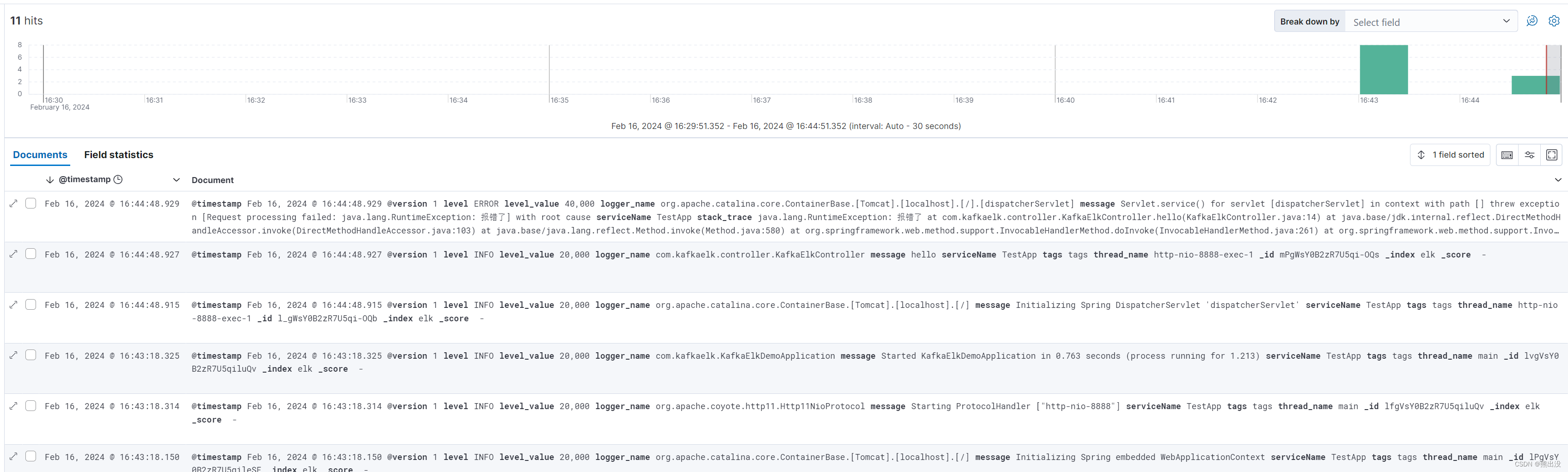
springboot集成elk实现日志采集可视化
一、安装ELK 安装ELK组件请参考我这篇博客:windows下安装ELK(踩坑记录)_windows上安装elk教程-CSDN博客 这里不再重复赘述。 二、编写logstash配置 ELK组件均安装好并成功启动,进入到logstash组件下的config文件夹,创建logstash.conf配置…...

leetcode 148. 排序链表 java解法
Problem: 148. 排序链表 思路 这是一个链表排序的问题,由于要求时间复杂度为 O(nlogn),适合使用归并排序(Merge Sort)来解决。 解题方法 首先,使用快慢指针找到链表的中间节点,将链表分成两部分。然后&…...
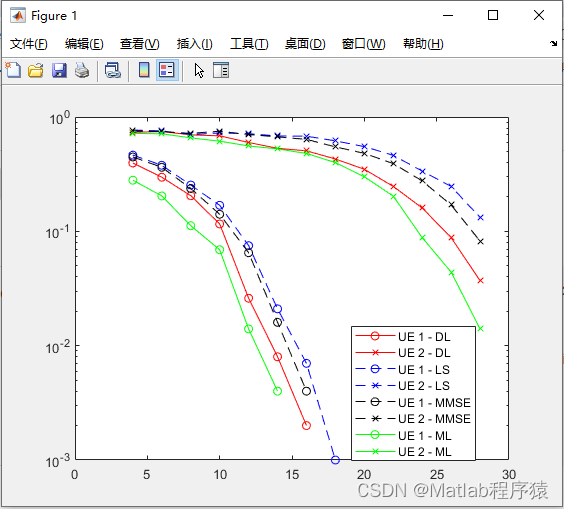
【MATLAB源码-第140期】基于matlab的深度学习的两用户NOMA-OFDM系统信道估计仿真,对比LS,MMSE,ML。
操作环境: MATLAB 2022a 1、算法描述 深度学习技术在无线通信领域的应用越来越广泛,特别是在非正交多址接入(NOMA)和正交频分复用(OFDM)系统中,深度学习技术被用来提高信道估计的性能和效率。…...

运动重定向学习笔记
目录 深度学习 重定向 2020年的模型: 重定向之后的bvh: 深度学习 重定向 输入是bvh,输出也是bvh...

导出Excel,支持最佳
列表信息导出为Excel文件, 依赖pom: Sheet, Row:<dependency><groupId>org.apache.poi</groupId><artifactId>poi</artifactId> </dependency>XSSFWorkbook <dependency><groupId>org.apache.poi</…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
