【感知机】感知机(perceptron)学习算法知识点汇总
机器学习——感知机
感知机(perceptron)是一种二分类的线性模型,属于判别模型,也称为线性二分类器。输入为实例的特征向量,输出为实例的类别(取+1和-1)。可以视为一种使用阶梯函数激活的人工神经元,例如通过梅尔频率倒谱系数(MFCC)对语音进行分类或通过图像的像素值对图像进行分类。
目录
感知机模型
感知机的几何解释
数据集的线性可分性
感知机学习策略
感知机学习算法
感知机学习算法的原始形式
感知机学习算法的对偶形式
算法的收敛性
感知机算法例题
感知机优缺点
感知机模型
定义 设输入空间(特征空间),输出空间
。输入
表示实例的特征向量,对应于输入空间的点,输出
表示实例的类别,由输入空间到输出空间的函数
称为感知机。
w,b为参数。叫做权值或权值向量(weight vector),b叫作偏置(bias)
符号函数sign的功能是取某个数的符号
感知机模型的假设空间是定义在特征空间中的所有线性分类模型或线性分类器,即函数集合
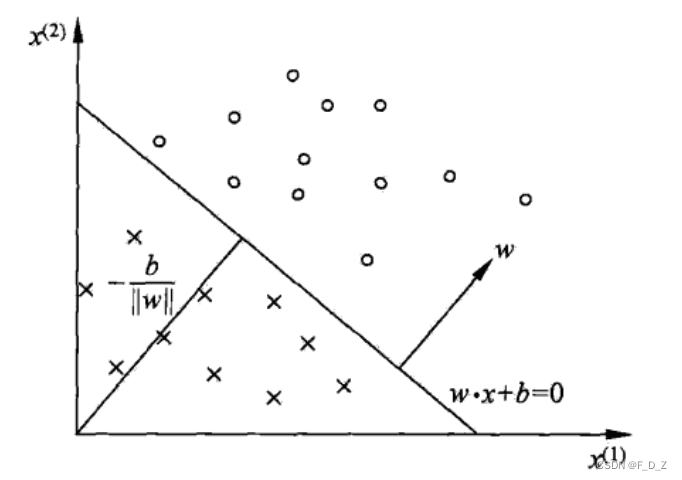
感知机的几何解释
:对应特征空间
中的一个超平面
,这个超平面将特征空间划分为两个部分,称为分离超平面(separating hyperplane)
b:超平面的截距
w:超平面的法向量
数据集的线性可分性
给定一个数据集,其中
,
,如果存在一个超平面
,能够正确地划分所有正负实例点,则称数据集
为线性可分数据集(linearky separable data set),否则称其线性不可分.
感知机学习策略
假设训练数据集线性可分
学习目标:求得正确划分训练集中所有正负实例点的分离超平面
学习策略:1、确定一个损失函数。2、选取使损失函数最小的参数。
损失函数的选择:误分类点到分离超平面的距离
任一点到超平面的距离公式:
,其中
是
的
范数,
向量的
范数:向量各元素平方和的平方根
定理1:对于误分类数据,有
从而由距离公式和定理1,得
误分类点到超平面的距离公式:
实现了去掉绝对值的工作
所有误分类点到超平面的总距离: ,
为误分类点集合
不必考虑,最终得到损失函数
损失函数:
一 个特定的样本点的损失函数:在误分类时是参数
的线性函数;在正确分类时是0。
因此,
给定训练数据集时,损失函数是
的连续可导函数
感知机学习算法
感知机学习算法的原始形式
输入:训练数据集,其中
,
,学习率
1.任意选取初值
2.任意顺序遍历,计算
,当
,转到步骤3;若对任意
,
,转到输出
3. ,
,转到步骤2.
输出:;感知机
算法采用随机梯度下降法(stochastic gradient descent):
首先任意选取一个超平面,然后用梯度下降法极小化损失函数。极小化过程不是一次使所有误分类点的梯度下降,而是每次随机选取一个误分类点使其梯度下降。
设误分类点集合M固定,损失函数
的梯度为:
对某点
,
的梯度
是增大的方向,故
使损失函数减少。
算法理解:当一个实例点被误分类时,则调整w,b的值,使分类超平面向该误分类点的一侧移动,减少该误分类点与超平面的距离,直至超平面越过该误分类点使其被正确分类
感知机学习算法的对偶形式
感知机学习算法的原始形式和对偶形式与支特向量机学习算法的原始形式和对偶形式相对应
输入:训练数据集,其中
,
,学习率
1.其中
2.任意顺序遍历,计算
,当
,转到步骤3;若对任意
,
,转到输出
3. ,
,转到步骤2
输出:;感知机
对偶形式的基本想法:将
和
表示为实例
和标记
的线性组合的形式,通过求解其系数来求解
和
基于原始形式,可设
,则迭代n次后,设第
个实例点由于误分而更新的次数为
,令
,有
,
。
注意:实例点更新次数越多,意味着它离分离超平面越近,意味着越难分类。这样的实例点对于学习结果的影响最大。
Gram矩阵:对偶形式中的训练实例仅以内积的形式出现,将实例间的内积计算出来并以矩阵的形式储存,
,称为Gram矩阵
算法的收敛性
算法原始形式收敛:意味着经过有限次迭代可得到一个将训练数据集完全正确划分的分离超平面
为便于推导,记,扩充输入向量,记
,则有
,
,
(Novikoff)定理 设训练集线性可分,其中
,
,则:
(1)存在满足的超平面
将训练数据集完全正确分开,且存在
,对所有
,
(2)令,则感知机学习算法在训练数据集上的误分类次数k满足不等式
定理表明,当训练数据集线性可分时,经过有限次搜索可以找到将训练数据集完全正确分开的超平面,即算法的原始形式收敛。
感知机算法例题
例1 训练数据集如图所示,正实例点为,
,负实例点为
,试用感知机算法原始形式求感知机模型,令
,

解答:
(1)建模最优化问题:
(2)取初值,
(3)按顺序,对
,
,则
为误分类点。更新
:
,
得到线性模型:
(4)重新选取,对,
,则均为正确分类点,不更新
;
对,
,则
为误分类点,更新
:
,
得到线性模型:
(5)由此不断迭代
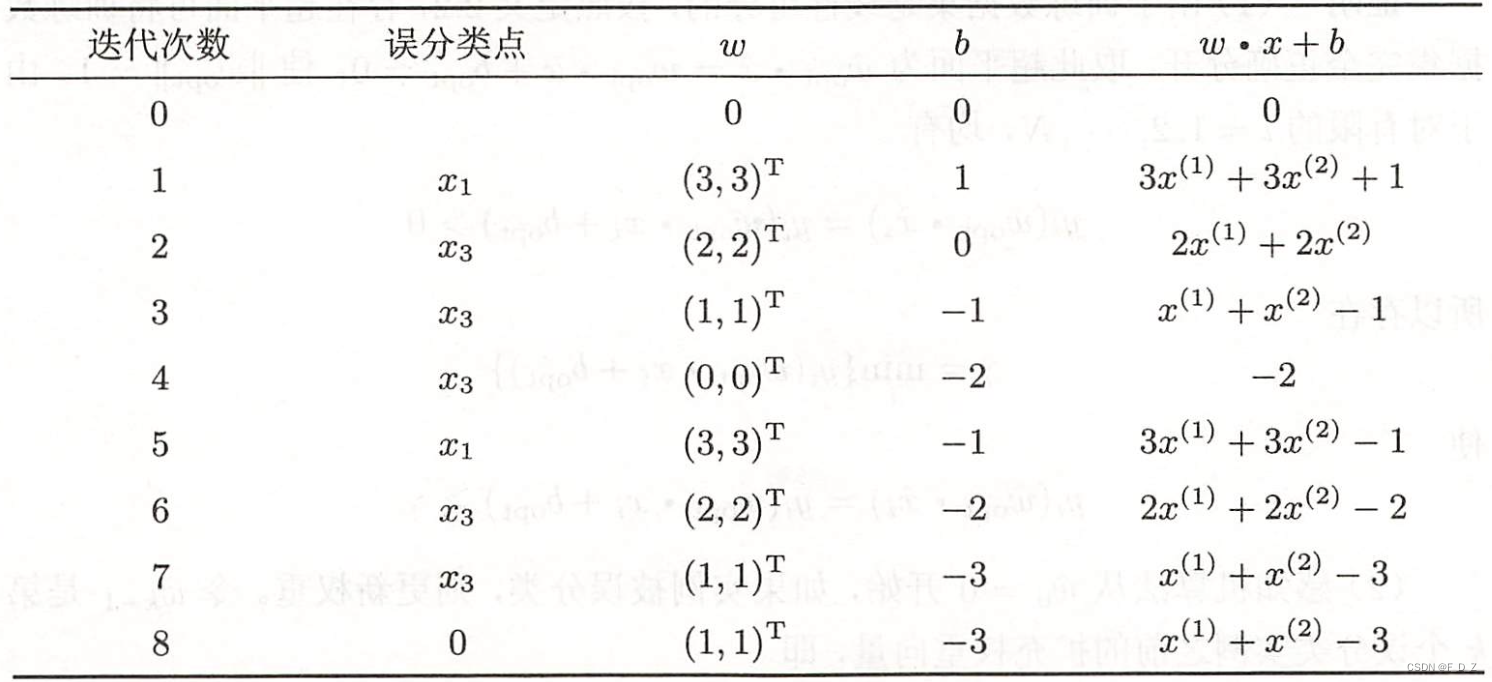
(6)直到,
线性模型:
对所有数据点,则确定分离超平面:
感知机模型
分离超平面
是按照
的取点顺序得到的
例1如果更换取点顺序为
,得到的分离超平面为:
由此,可知结论:感知机算法采用不同的初值或选取不同的误分类点顺序,解可以不同
例2 训练数据集如图所示,正实例点为,
,负实例点为
,试用感知机算法对偶形式求感知机模型,令
,
解答:
(1)取;
(2)计算Gram矩阵
(3)误分条件
(4)参数更新
(5)迭代
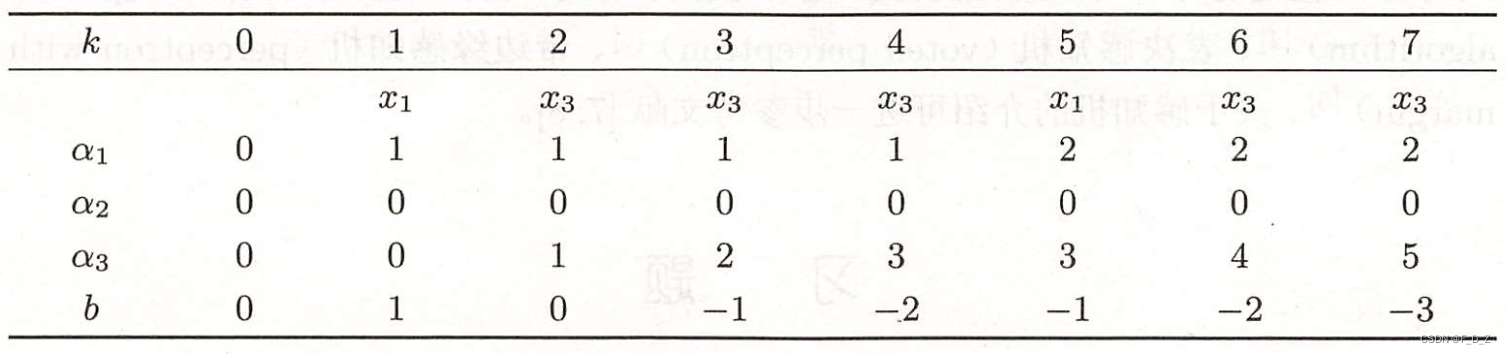
(6)最终得到
则,分离超平面:
感知机模型:
与原始形式一致,感知机学习算法的对偶形式迭代收敛,且存在多个解
感知机优缺点
优点:简单、易于实现、运行速度快
缺点:仅处理线性可分问题,面对多类别多分类问题需要多个分类器导致训练成本增加
在例题的实际操作中可以发现,感知机学习算法存在许多解,这些解既依赖于初值的选择,也依赖于选代过程中误分类点的选择顺序。而为了得到唯一的超平面,需要对分离超平面增加约束条件,这就涉及到了线性支持向量机的想法。
相关文章:
【感知机】感知机(perceptron)学习算法知识点汇总
机器学习——感知机 感知机(perceptron)是一种二分类的线性模型,属于判别模型,也称为线性二分类器。输入为实例的特征向量,输出为实例的类别(取1和-1)。可以视为一种使用阶梯函数激活的人工神经元,例如通过梅尔频率倒谱系数(MFCC…...

蓝桥杯:C++二分算法
在基本算法中,二分法的应用非常广泛,它是一种思路简单、编程容易、效率极高的算法。蓝桥杯软件类大赛中需要应用二分法的题目很常见。 二分法有整数二分和实数二分两种应用场景 二分法的概念 二分法的概念很简单,每次把搜索范围缩小为上一…...

Leetcode刷题笔记题解(C++):83. 删除排序链表中的重复元素
思路:链表相关的问题建议就是画图去解决,虽然理解起来很容易,但就是写代码写不出来有时候,依次去遍历第二节点如果与前一个节点相等则跳过,不相等则遍历第三个节点 /*** Definition for singly-linked list.* struct …...
|Day56(动态规划))
@ 代码随想录算法训练营第8周(C语言)|Day56(动态规划)
代码随想录算法训练营第8周(C语言)|Day56(动态规划) Day56、动态规划(包含题目 ● 300.最长递增子序列 ● 674. 最长连续递增序列 ● 718. 最长重复子数组 ) 300.最长递增子序列 题目描述 给你一个整数…...
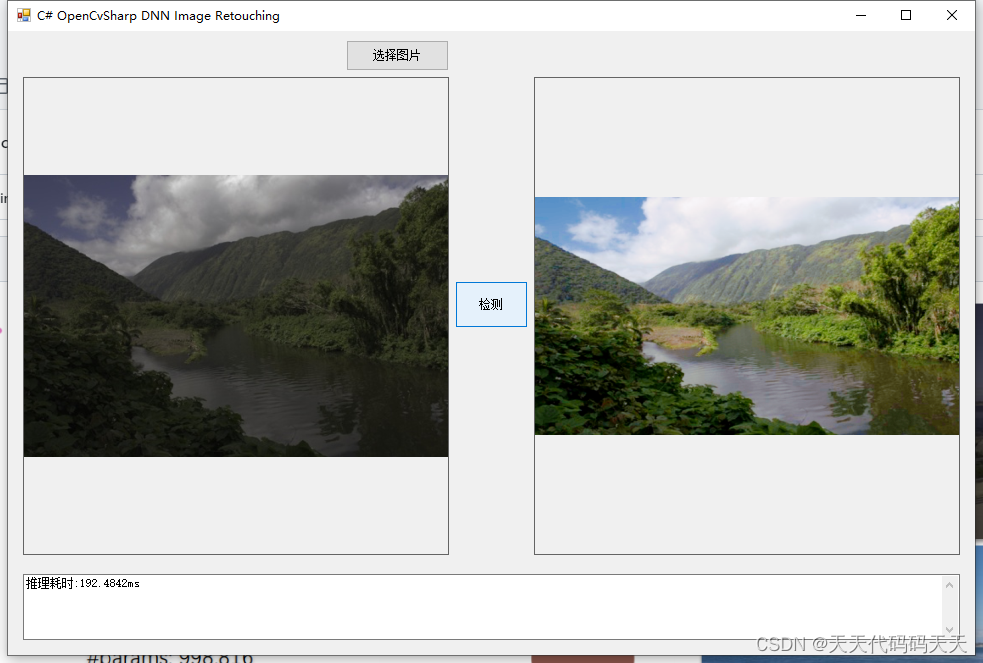
C# OpenCvSharp DNN Image Retouching
目录 介绍 模型 项目 效果 代码 下载 C# OpenCvSharp DNN Image Retouching 介绍 github地址:https://github.com/hejingwenhejingwen/CSRNet (ECCV 2020) Conditional Sequential Modulation for Efficient Global Image Retouching 模型 Model Properti…...

通过Docker Compose的方式在Docker中安装Maven环境
目前可以说 Docker 已经是在开发部署中成为主流,所以我们很多环境和工具都会安装在 Docker 容器中,Maven 环境是 SpringBoot 项目中最常用的依赖管理工具。当我们使用自动运维工具如 Ansible、Chef 、Puppet、Walle、Spug等)管理和部署 Maven…...
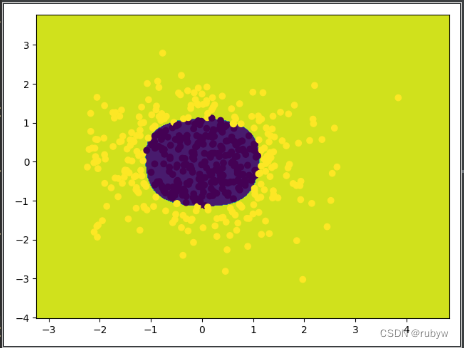
Python实现线性逻辑回归和非线性逻辑回归
线性逻辑回归 # -*- coding: utf-8 -*- """ Created on 2024.2.20author: rubyw """import matplotlib.pyplot as plt import numpy as np from sklearn.metrics import classification_report from sklearn import preprocessing from sklearn…...

【软考】软件维护
目录 一、说明二、正确性维护三、适应性维护四、完善性维护五、预防性维护 一、说明 1.软件维护主要是根据需求变化或硬件环境的变化对应用程序进行部分或全部修改 2.修改时应充分利用源程序,修改后要填写程序修改登记表,并在程度变更通知书上写明新旧程…...

突破性创新:OpenAI推出Sora视频模型,预示视频制作技术的未来已到来!
一、前言 此页面上的所有视频均由 Sora 直接生成,未经修改。 OpenAI - Sora is an AI model that can create realistic and imaginative scenes from text instructions. 2024 年 2 月 16 日,OpenAI 发布 AI 视频模型 Sora,60 秒的一镜到底…...
【Web前端笔记10】CSS3新特性
10 CSS3新特性 1、圆角 2、阴影 (1)盒阴影 3、背景渐变 (1)线性渐变(主要掌握这种就可) (2)径向渐变 &…...

LabVIEW荧光显微镜下微管运动仿真系统开发
LabVIEW荧光显微镜下微管运动仿真系统开发 在生物医学研究中,对微管运动的观察和分析至关重要。介绍了一个基于LabVIEW的仿真系统,模拟荧光显微镜下微管的运动过程。该系统提供了一个高效、可靠的工具,用于研究微管与运动蛋白(如…...

【Java面试】MQ(Message Queue)消息队列
目录 一、MQ介绍二、MQ的使用1应用解耦2异步处理3流量削峰4日志处理5消息通讯三、使用 MQ 的缺陷1.系统可用性降低:2.系统复杂性变高3.一致性问题四、常用的 MQActiveMQ:RabbitMQ:RocketMQ:Kafka:五、如何保证MQ的高可用?ActiveMQ:RabbitMQ:RocketMQ:Kafka:六、如何保…...
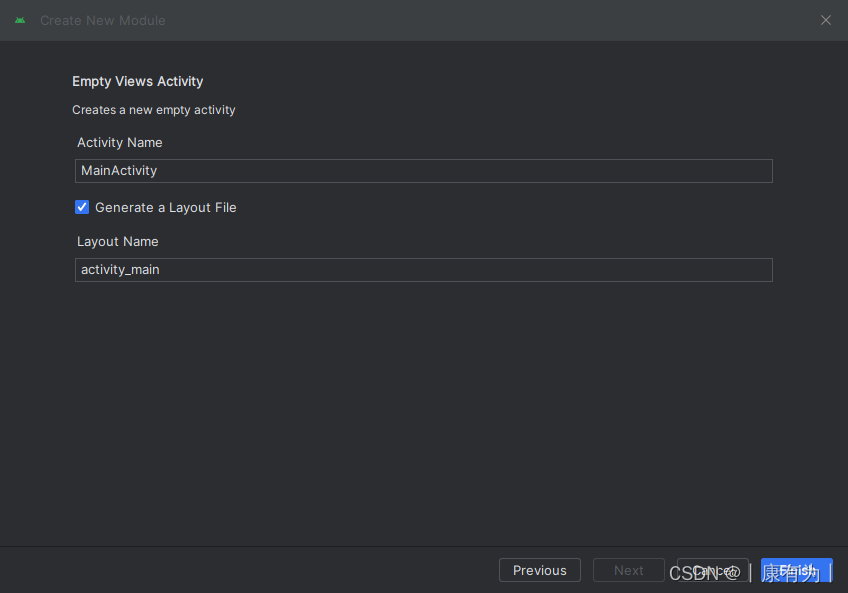
【安卓基础1】初识Android
🏆作者简介:|康有为| ,大四在读,目前在小米安卓实习,毕业入职。 🏆安卓学习资料推荐: 视频:b站搜动脑学院 视频链接 (他们的视频后面一部分没再更新,看看前面…...
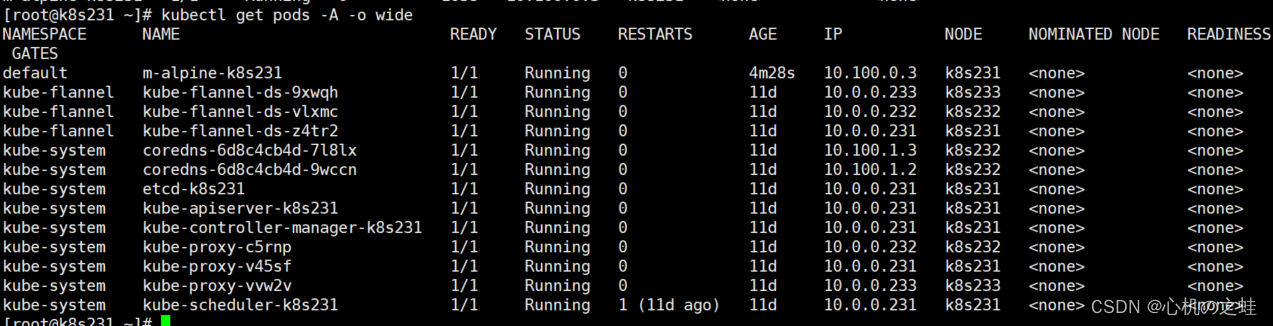
08-静态pod(了解即可,不重要)
我们都知道,pod是kubelet创建的,那么创建的流程是什么呐? 此时我们需要了解我们k8s中config.yaml配置文件了; 他的存放路径:【/var/lib/kubelet/config.yaml】 一、查看静态pod的路径 [rootk8s231 ~]# vim /var/lib…...
PROBIS铂思金融破产后续:ASIC牌照已注销
2024年1月31日,PROBIS铂思金融的澳大利亚ASIC牌照 (AFSL 338241) 被注销《差价合约经纪商PROBIS宣布破产,澳大利亚金融服务牌照遭暂停》,这也就意味着,PROBIS铂思金融目前已经没有任何金融牌照。 值得注意的是,时至今日…...

数字世界的探索者:计算机相关专业电影精选推荐
目录 推荐计算机专业必看的几部电影 《黑客帝国》 《社交网络》 《乔布斯传》 《心灵捕手》 《源代码》 《盗梦空间》 《头号玩家》 《我是谁:没有绝对安全的系统》 《战争游戏》(WarGames) 《模仿游戏》(The Imitation Game) 《硅谷》(Silicon Valley) …...

Spring Boot项目中TaskDecorator的应用实践
一、前言 TaskDecorator是一个执行回调方法的装饰器,主要应用于传递上下文,或者提供任务的监控/统计信息,可以用于处理子线程与主线程间数据传递的问题。 二、开发示例 1.自定义TaskDecorator import org.springframework.core.task.Task…...

511. 游戏玩法分析 I
文章目录 题意思路代码 题意 题目链接 统计每个用户第一次登陆平台时间 思路 代码 select player_id, min(event_date) as first_login from Activity group by player_id;...
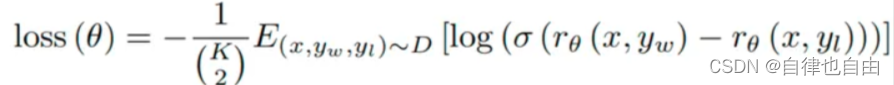
大模型训练流程(三)奖励模型
为什么需要奖励模型 因为指令微调后的模型输出可能不符合人类偏好,所以需要利用强化学习优化模型,而奖励模型是强化学习的关键一步,所以需要训练奖励模型。 1.模型输出可能不符合人类偏好 上一篇讲的SFT只是将预训练模型中的知识给引导出来…...

替换if...else的锦囊妙计
目录 前言 一、又臭又长的if...else 二、消除if...else的锦囊妙计 1、使用注解 2、动态拼接名称 3、模板方法判断 4.策略工厂模式 5.责任链模式 6、其他的消除if...else的方法 1.根据不同的数字返回不同的字符串 2.集合中的判断 3.简单的判断 4.spring中的判断 原文…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...
