LeetCode23.合并K个升序链表
题目
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 :
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
思路
要将多个已按升序排列的链表合并成一个升序链表,可以使用分治法的思想。我们利用分治法的思想,递归地将链表数组拆分成两部分,然后合并这些部分,最终得到一个合并后的升序链表。
-
定义一个辅助函数mergeTwoLists(ListNode* list1, ListNode* list2),用于合并两个链表的方法,这是我们之前讨论过的合并两个升序链表的方法。
-
在mergeKLists函数中,首先判断输入的链表数组是否为空,如果为空则返回nullptr。
-
利用分治法的思想,将链表数组不断地拆分成两部分,然后递归地合并这些部分,直到只剩下一个链表为止。具体步骤如下:
- 计算链表数组的中间位置mid,将链表数组拆分成两部分:左半部分为[0, mid-1],右半部分为[mid, size-1]。
- 递归调用mergeKLists函数,分别对左右两部分进行合并,得到leftList和rightList。
- 最终,再调用mergeTwoLists方法将leftList和rightList合并为一个新的升序链表,并返回合并后的结果。
-
最终返回合并后的链表即可。
Code:
class Solution {
public:ListNode* mergeKLists(vector<ListNode*>& lists) {if (lists.empty()) {return nullptr;}return merge(lists, 0, lists.size() - 1);}private:ListNode* merge(vector<ListNode*>& lists, int left, int right) {if (left == right) {return lists[left];}if (left < right) {int mid = left + (right - left) / 2;ListNode* leftList = merge(lists, left, mid);ListNode* rightList = merge(lists, mid + 1, right);return mergeTwoLists(leftList, rightList);}return nullptr;}ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {if (!list1) {return list2;}if (!list2) {return list1;}if (list1->val < list2->val) {list1->next = mergeTwoLists(list1->next, list2);return list1;} else {list2->next = mergeTwoLists(list1, list2->next);return list2;}}
};
相关文章:

LeetCode23.合并K个升序链表
题目 给你一个链表数组,每个链表都已经按升序排列。 请你将所有链表合并到一个升序链表中,返回合并后的链表。 示例 : 输入:lists [[1,4,5],[1,3,4],[2,6]] 输出:[1,1,2,3,4,4,5,6] 解释:链表数组如下&…...
(01)Hive的相关概念——架构、数据存储、读写文件机制
目录 一、架构及组件介绍 1.1 Hive整体架构 1.2 Hive组件 1.3 Hive数据模型(Data Model) 1.3.1 Databases 1.3.2 Tables 1.3.3 Partitions 1.3.4 Buckets 二、Hive读写文件机制 2.1 SerDe 作用 2.2 Hive读写文件流程 2.2.1 读取文件的过程 …...
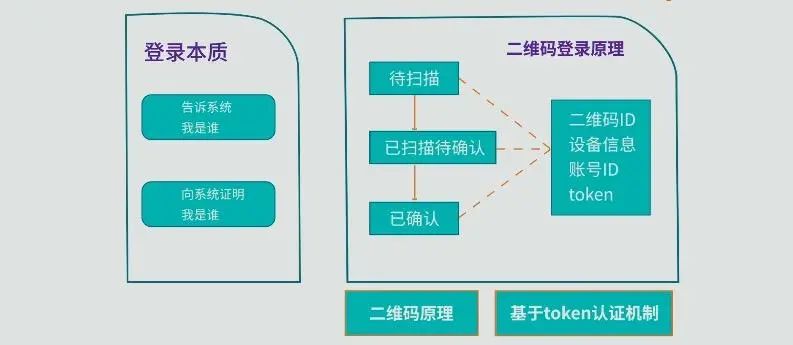
二维码扫码登录原理,其实比你想的要简单的多
二维码,大家再熟悉不过了 购物扫个码,吃饭扫个码,坐公交也扫个码 在扫码的过程中,大家可能会有疑问:这二维码安全吗? 会不会泄漏我的个人信息? 更深度的用户还会考虑:我的系统是不…...
)
Java 实现 Awaitable(多线程并行等待,类似 AutoEventReset 的作用)
AutoEventReset、ManualEventReset,是我们在多线程并行编程之中常常需要涉及的,但是 ManualEventReset 可能用的并没有那么多,这个多用于实现读写锁的,当然 Java 自己库提供了官方实现,就没必要自己去整了。 C/C 里面…...

AI之Sora:Sora(文本指令生成视频的里程碑模型)的简介(能力/安全性/技术细节)、使用方法、案例应用之详细攻略
AI之Sora:Sora(文本指令生成视频的里程碑模型)的简介(能力/安全性/技术细节)、使用方法、案例应用之详细攻略 导读:Sora 是OpenAI研发的一个可以根据文字描述生成视频的AI模型。它的主要特性、功能以及OpenAI在安全和应用方面的策略的核心要点如下所示&a…...

IListManger feeds流
目的:将feeds的分页加载和下拉刷新,与网络请求关联起来 ListLibRecyclerViewProxy 在this.getRecyclerView().addOnScrollListener中记录事件 recyclerView.computeVerticalScrollOffset() // 已经向下滚动的距离,为0时表示已处于顶部。 recyclerView.computeVerticalScro…...
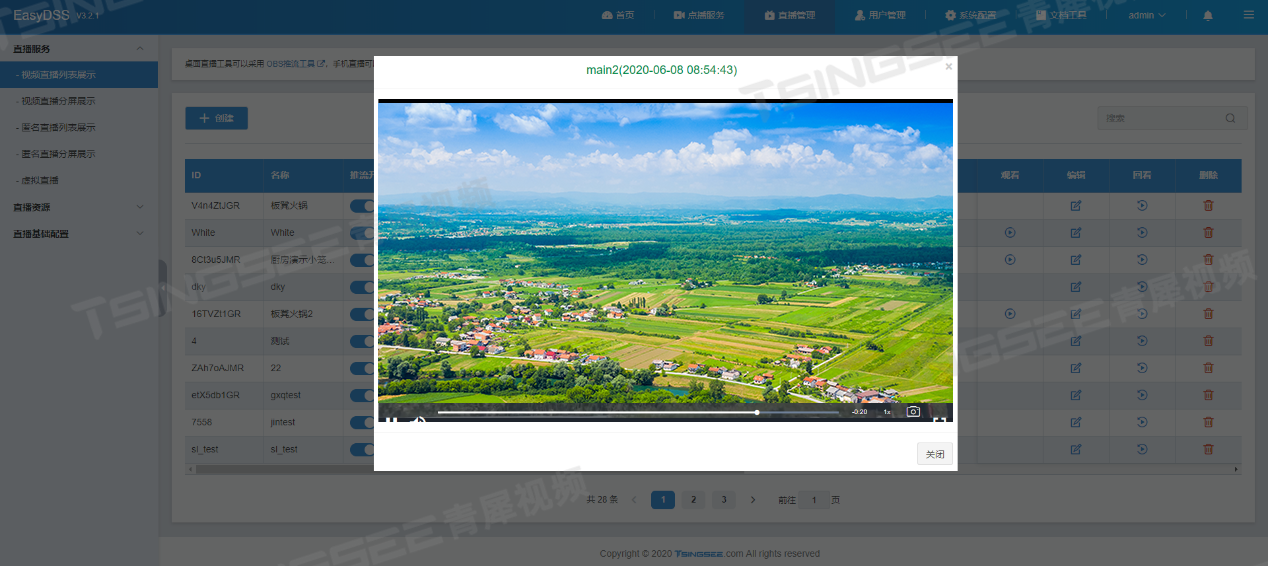
视频推拉流EasyDSS视频直播点播平台授权出现激活码无效并报错400是什么原因?
视频推拉流EasyDSS视频直播点播平台集视频直播、点播、转码、管理、录像、检索、时移回看等功能于一体,可提供音视频采集、视频推拉流、播放H.265编码视频、存储、分发等视频能力服务,在应用场景上,平台可以运用在互联网教育、在线课堂、游戏…...

设计模式三:工厂模式
工厂模式包括简单工厂模式、工厂方法模式和抽象工厂模式,其中后两者属于23中设计模式 各种模式中共同用到的实体对象类: //汽车类:宝马X3/X5/X7;发动机类:B48TU、B48//宝马汽车接口 public interface BMWCar {void s…...
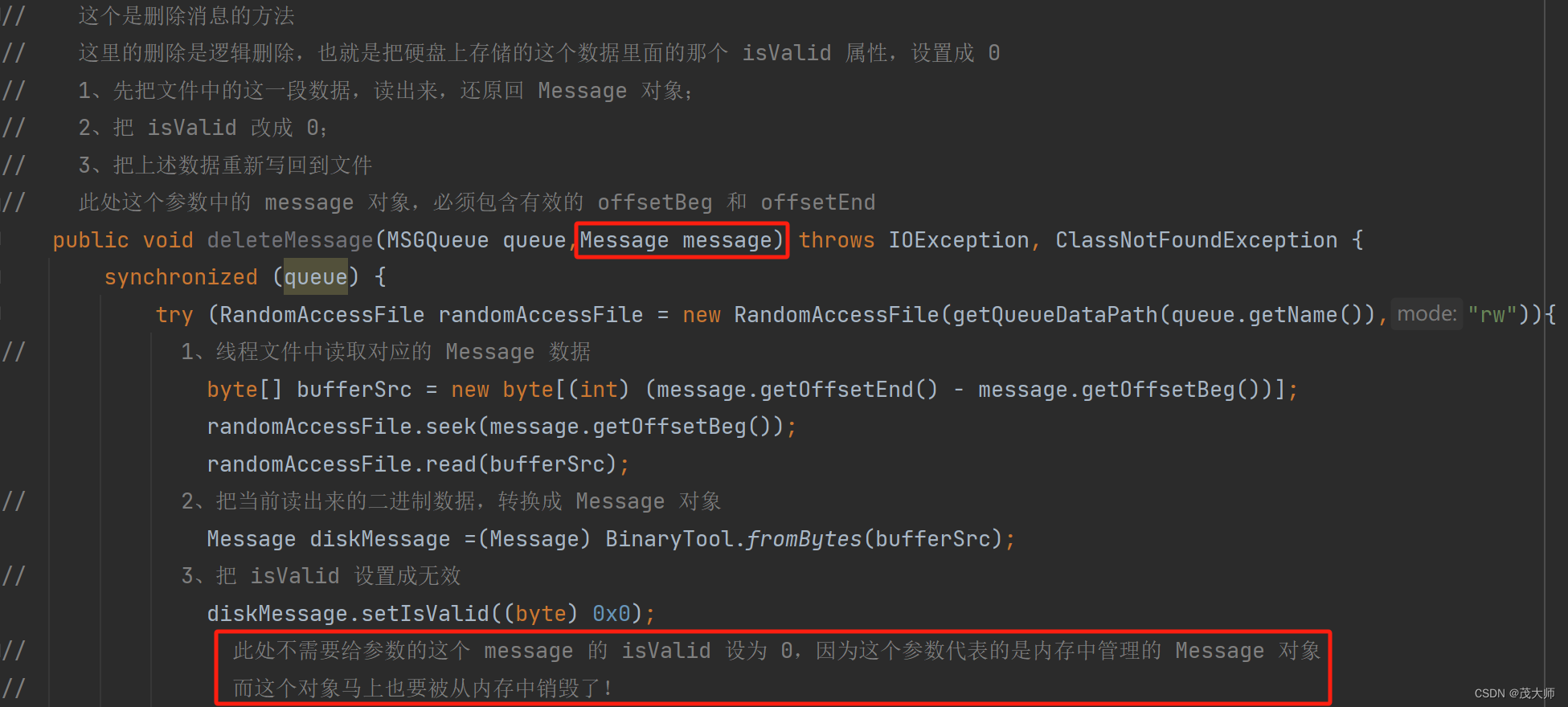
2024.2.15 模拟实现 RabbitMQ —— 消息持久化
目录 引言 约定存储方式 消息序列化 重点理解 针对 MessageFileManager 单元测试 小结 统一硬盘操作 引言 问题: 关于 Message(消息)为啥在硬盘上存储? 回答: 消息操作并不涉及到复杂的增删查改消…...

【技巧】金融企业在搭建服务器时,选择私有云方案还是全栈专属云?
金融企业在搭建服务器时,选择私有云方案还是全栈专属云,需要根据企业的具体需求和情况进行综合考虑。Cloud Ace云一作为谷歌云全球战略合作伙伴,专注于企业级出海云服务 ,为大家带来两种方案的优劣势比较: 私有云 优势…...
模型评测)
【大厂AI课学习笔记】【2.2机器学习开发任务实例】(10)模型评测
目录 一、模型评测的定义 二、模型评测的方法 三、模型评测的原理 四、涉及的关键技术 五、实例阐述 今天是2.2机器学习开发任务实例的最后一个部分——模型评测。 不同的模型计算出的MSE值会有差异,通过模型的选择,参数的变换,可以比较…...
【C++游戏开发-03】贪吃蛇
文章目录 前言一、工具准备1.1游戏开发框架1.2visual studio2022下载1.3easyX下载1.4图片素材 二、逻辑分析2.1数据结构2.2蛇的移动2.3吃食物2.4游戏失败 三、DEMO代码实现四、完整源代码总结 🐱🚀个人博客https://blog.csdn.net/qq_51000584?typeblo…...
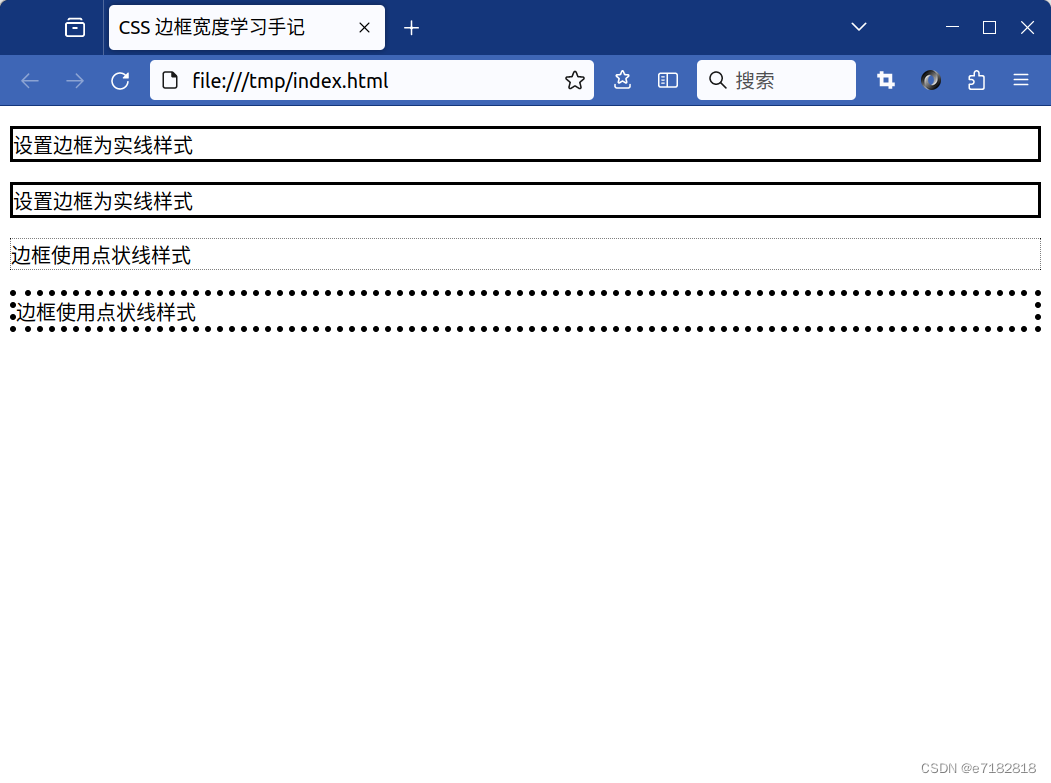
如何理解CSS的边框宽度?
CSS 边框宽度学习手记 CSS 边框宽度小概念 在CSS的世界里,border-width这个属性真的很实用,它能帮我指定HTML元素四周边框的宽度。这个宽度嘛,可以用像素px、点pt、厘米cm、相对单位em这些来表示,很方便吧!还有呢&am…...

java 写入写出 zip
package com.su.test.aaaTest.ioTest; import java.io.File; import java.io.FileInputStream; import java.io.FileOutputStream; import java.io.IOException; import java.util.zip.ZipEntry; import java.util.zip.ZipOutputStream; /** 将文件压缩到 zip 中 */ public c…...
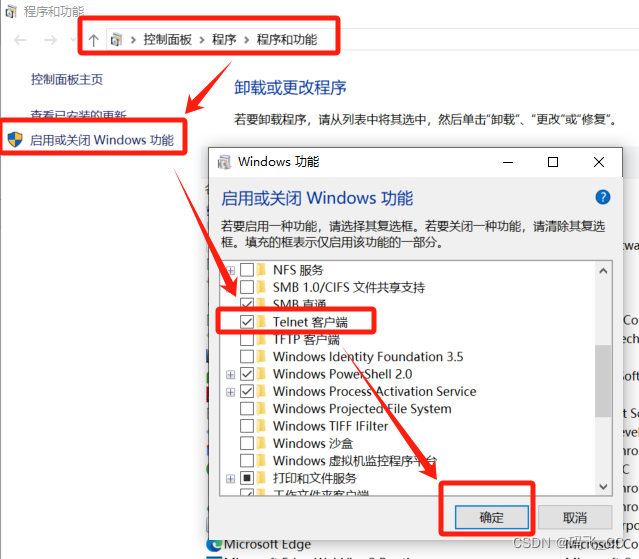
问题解决:‘telnet‘ 不是内部或外部命令,也不是可运行的程序 或批处理文件
当在windows终端中运行telnet指令的时候,发现指令不可用,原因在于系统没安装telnet功能。 解决方法: 打开控制面板–》程序–》启用或关闭windows功能–》勾选Telnet客户端,点击确定即可。...

从基础到高级:Linux用户与用户组权限设置详解
目录 博客前言: 一.简介 1.用户的定义 用户账户分类 2.用户组的定义 二.用户的相关linux语法 1.创建用户(useradd) 2.删除用户(userdel) 3.修改用户(usermod) 4.修改用户密码 5.su切…...
【感知机】感知机(perceptron)学习算法知识点汇总
机器学习——感知机 感知机(perceptron)是一种二分类的线性模型,属于判别模型,也称为线性二分类器。输入为实例的特征向量,输出为实例的类别(取1和-1)。可以视为一种使用阶梯函数激活的人工神经元,例如通过梅尔频率倒谱系数(MFCC…...

蓝桥杯:C++二分算法
在基本算法中,二分法的应用非常广泛,它是一种思路简单、编程容易、效率极高的算法。蓝桥杯软件类大赛中需要应用二分法的题目很常见。 二分法有整数二分和实数二分两种应用场景 二分法的概念 二分法的概念很简单,每次把搜索范围缩小为上一…...

Leetcode刷题笔记题解(C++):83. 删除排序链表中的重复元素
思路:链表相关的问题建议就是画图去解决,虽然理解起来很容易,但就是写代码写不出来有时候,依次去遍历第二节点如果与前一个节点相等则跳过,不相等则遍历第三个节点 /*** Definition for singly-linked list.* struct …...
|Day56(动态规划))
@ 代码随想录算法训练营第8周(C语言)|Day56(动态规划)
代码随想录算法训练营第8周(C语言)|Day56(动态规划) Day56、动态规划(包含题目 ● 300.最长递增子序列 ● 674. 最长连续递增序列 ● 718. 最长重复子数组 ) 300.最长递增子序列 题目描述 给你一个整数…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
