信息安全与数学基础-笔记-②同余
知识目录
- 同余
- 完全剩余系
- 剩余类
- 完全剩余系
- ❀简化剩余系❀
- 欧拉函数
- 逆元
- !欧拉定理 !
同余
a,b 两个数字,都模m,当两个数字模m后余的数一样即为同余。
例子:
a = bq + r (mod m),这里的a 和 r 就是同余 ,因为a模m就是余r的
-
同余性质:若 m | a-b 则 a 和 b 同余 m,同余符号用三横线表示

-
传递性:若:a b同余 ,b c 同余,那么a和c就同余
-
倍数原则:a和b模m同余,则a = km + b
解释:同余中玩的也是余数,所以当模m余数相同的时候,不管你添加多少个m都是同余的结果 -
加法原则:a b 同余,c d 同余,则a + c 和 b + d也同余
解释:原因是因为a 和 b的余数是相同的,只要两边添加相同的数字便不会改变ab之间还是同余的关系,那么上面添加的是 c 和 d,明显cd本身就是同余,也就是说ab添加的不是cd而是cd的余数,他们的余数是一样的,也就是两边添加后还是同余的结果。 -
乘法原则:a b 同余,c d 同余,则a × c 和 b × d也同余
解释:同理,本质是用余数进行运算,所以相乘也是两边乘以同一个数字后还是同余的。
注意:乘法成立,除法不成立 -
乘法原则推论:a b 模m同余,则:na 和 nb同余,n为任意整数
解释:余数同乘则不变 -
指数原则:若ab同余,则:ana^nan和bnb^nbn也同余
解释:因为a和b同余,次方数也一样,个数一样的a和b相乘,其实也就是和乘法原则一样,所以指数原则只要次方数一样也是同余。 -
单独原则:a + b mod m == a mod m + b mod m 或者 当ab同余的时候,na和nb在判断是否同余的时候,也可以单独先对ab分开取模,例如:n (a mod m) = n (b mod m)
解释:在一个求模式子中,可以单独拆开来分别先取模,同理在乘法中也一样,两个数字相乘,也可以单独拆开来分别取模,这和十进制运算也是一样的道理。 -
同除原则:若ad 和 bd 模 m同余,(d,m) = 1,则:a 同余 b
解释:上面的乘法原则提到除法不行,但是这里又可以?因为这里的d是和m互素的,所以我们可以用单独原则,将两边的d进行先取模,最后得到一个1和ab相乘,所以最后得出ab是同余的,所以在希望通过除法对数字简化的时候必须要保证两边的数字能够提取出来的公因数是与m互素的才能够保证之后的数字仍为同余。 -
若ab模m同余 ,取k,k>0,则:同乘k后ak bk 模mk仍然同余
解释:这里的k并没有考虑是否和m互素或者与其他数字有什么联系,我们不考虑这些关系后把m也同时乘k,这时候当我们再把ak取模的时候会把k一同消去,留下的只有a的余数,同理bk也是留下了b的余数,那么就和原本的ab模m同余一样了。对比上面同乘原则这里更多的是考虑整体,而同乘原则考虑的是余数之间,因为同余的余数相等,同乘k是依旧同余,但余数余数不一样了,变成了k倍了,但是这里是整体乘k,取模的时候是整体模k,所以,模完之后的余数仍然和原本的ab模m后的余数使用一样的,因此这两个定理是不一样的。 -
若ak bk 模mk同余,则:a b 模 m同余
解释:其实是上一条定理的推论,但是要把模数也除,因为这里的k并没有和模数mk互素,因此也要都除。为什么不叫同除:因为同的意思是同余的两个数的同除,不关模数的事情,但这里把模数也除了,所以不叫同除原则了(好牵强的解释)。
把ak bk mk换成c d e,那么推论就是:cd模e同余,那么c/k d/k 模e/k同余 -
假如:a 三 b (mod m1) ,a 三 b (mod m2)
那么求出m1,m2的最小公倍数为 G
则:a 三 b (mod G) 同余。
(PS:这里的定理在后面的方程组中,如果发现一个数字可以拆分成m1,m2,mi…相乘,并且两两互素的时候就可以减少计算量) -
总结
“同”的字眼一般是对同余符号两边的数字进行操作,和模数没有关系
因此:同乘k模m仍旧同余,但余数若没有超出模数大小就变成了余数的k倍。同除就是能将两边的数提取公因数,并且该公因数需要和模数互素才可以同除。
以下说的就是和模数有关的,当两边的数和模数都能提取出一个公共的公因数就可以一并提取,也可以无缘无故的同时乘一个k数进去,涉及到模数改变的,一般改变之后,和原本的式子的余数一样。
完全剩余系
完全剩余系是由剩余类中的数字组成的。
是等于模m中 ,0~m-1的数字就是完全剩余系,即两两不同余。
剩余类
当模m后,每一个数字都不会大于m,那么在0~m-1个数字中,每个数字代表了一个剩余数字,因为在模的世界里, 比如1模m余数为1,也就是剩余为1的一类,当1加上模数m的时候,再去模m后还是1,所以余数为1的数字很多,把这些数字统一起来叫余数为1的剩余类
设:
C0C_0C0 代表余数为0的一类
C1C_1C1 代表余数为1的一类
C2C_2C2 代表余数为2的一类
C3C_3C3 代表余数为3的一类,以此类推
这就是剩余类,剩余类有m个,范围是[0, m-1]
- 剩余类之间的关系
①每个数字都同余
②剩余类内的数字可以是无限大,只要是余数和剩余类内其他数字同余即可
③剩余类内任意取出一个数,该数叫做该类的剩余
完全剩余系
当模m后,我们在每一个剩余类中取出一个数字来组成一个整体,那么该整体就叫做完全剩余系。
- 完全剩余系之间的关系
①每个数字之间都不同余
②每个数字模m后组成0~m-1的数字
③该系中的数字可以无限大,只要不和其他数字同余即可
完全剩余系的性质
- 若**(a,m) = 1**,设r0r_0r0,r1r_1r1,r2r_2r2…rmr_mrm为模m的一个完全剩余系
那么:ar0r_0r0 + b, ar1r_1r1 + b, ar2r_2r2 + b, … armr_mrm + b, 仍然是模m的一个完全剩余系,该性质完全就是应用了同余知识,当a和m互素的时候就能够将原本的数字改变后仍和原来的数字是同余的,所以在完全剩余系中都不同余的数字,每一个数字改变后其实还是和原来的数字是一样的,所以其实还是原来的剩余系没有改变,仍旧是都不同余的数字,只是数字本身进行了一些变化,其他数字也会跟着变化,所以剩余系还是那个剩余系。 - 完全剩余系的应用

解释该定理是如何操作的:
一:随便找出两个互素的正整数的完全剩余系,设两个数:m1m_1m1m2m_2m2
二:说明:待会公式中,x1x_1x1,x2x_2x2 会分别 遍历 m1m_1m1,m2m_2m2的完全剩余系
(x1遍历m1,x2遍历m2)
三:公式:x1x_1x1×m2m_2m2 + x2x_2x2×m1m_1m1 ,其中x1x_1x1,x2x_2x2就开始遍历
四:遍历得到的多个数字,x1x_1x1×m2m_2m2 + x2x_2x2×m1m_1m1 其实就是模m1m_1m1×m2m_2m2的完全剩余系。
❀简化剩余系❀
简化剩余系就是在完全剩余系中找出与模数m互素的剩余类,将其留下来组成的整体就是简化剩余系。
举例:模数为8的时候
C1C_1C1 C3C_3C3 C5C_5C5 就是模8的简化剩余系,其他剩余类中的0 2 4都不是和8互素的
欧拉函数
模m的简化剩余系中的个数,叫做欧拉函数:ϕ\phiϕ(m)
其他运算和简化剩余系一样,一些简单的运算后保证还是简化剩余系即可。
- 若p为素数,ϕ(p)\phi(p)ϕ(p) = p - 1
- 若mn互素,即(m,n) = 1,则ϕ\phiϕ(mn) = ϕ\phiϕ(m)ϕ\phiϕ(n)
- 若p为素数,ϕ\phiϕ(pap^apa) = pap^apa - pap^apa −^-− 1^11
- 若p,q为素数,并且n = p×q,则ϕ\phiϕ(n) = (p-1)(q-1)
- 欧拉函数求解通式
设n为欧拉函数的参数
求出n的标准分解式:n = p1p_1p1a^aa1^11×p2p_2p2a^aa2^22×p3p_3p3a^aa3^33…
则:ϕ\phiϕ(n) = n × (1- 1/p1p_1p1 ) × (1- 1/p2p_2p2 ) × (1- 1/p3p_3p3 )
欧拉函数求解的通式十分重要
逆元
设:(a,m) = 1,a×a−a^-a−三 1 mod m
a−a^-a−就是a的逆元,相当于分数中的倒数,一个数乘以他的倒数就等于1,在同余中同理,当一个数乘以逆元,就同余1.
如何求逆元:
对(a,m)使用欧几里德算法后使用裴蜀等式算出s和t,也就是sa + tm = 1后,很明显,要找a的逆元就是s,因为tm模m后是0,只剩下sa = 1所以逆元就是s
!欧拉定理 !
欧拉定理必须要记住,在后续解方程或者计算高次幂的数字时候能大大减少计算量。
- aϕa^\phiaϕ(^((m^mm)^)) 三 1 (mod m)
费马小定理
apa^pap−^-−1^11 三 1 (mod p)
解释:其实就是应用了欧拉定理中的方法,当p是素数的时候ϕ(p)\phi(p)ϕ(p) = p-1
相关文章:

信息安全与数学基础-笔记-②同余
知识目录同余完全剩余系剩余类完全剩余系❀简化剩余系❀欧拉函数逆元!欧拉定理 !同余 a,b 两个数字,都模m,当两个数字模m后余的数一样即为同余。 例子: a bq r (mod m),这里的a 和 r 就是同余 ÿ…...

网络安全法
目录正文第一章第二章第三章第四章第五章第六章 法律责任第七章 附则正文 学习网络安全应该知道网络安全法 第一章 总则 第一条: 为了保障网络安全,维护网络空间主权和国家安全、社会公共利益,保护公民、法人和其他组织的合法权益,促进经济…...

django框架开发部署项目
前言:相信看到这篇文章的小伙伴都或多或少有一些编程基础,懂得一些linux的基本命令了吧,本篇文章将带领大家服务器如何部署一个使用django框架开发的一个网站进行云服务器端的部署。 文章使用到的的工具 Python:一种编程语言&…...

Unity记录1.3-入门-第一阶段总结
文章首发及后续更新:https://mwhls.top/4447.html,无图/无目录/格式错误/更多相关请至首发页查看。 新的更新内容请到mwhls.top查看。 欢迎提出任何疑问及批评,非常感谢! 汇总:Unity 记录 摘要:第一阶段的总…...

Linux入门篇-文件管理
简介 简单的文件管理。 ⽂件内容的查看 ⽂本⽂件内容的查看 cat ⽂本⽂件的path1 ⽂本⽂件的path2 head ⽂本⽂件的path ,显示⽂件的前10⾏内容 head -n 5 ⽂本⽂件的path , 显示⽂件的前5⾏内容 head -5 等于head -n 5tail ⽂本⽂件的path, 显示⽂件的后10⾏内容…...

如何从错误中成长?
在上一篇文章“技术人的犯错成本”里,我和你聊了技术人可能会犯的各式各样的错误,也举了很多例子,说明了技术人犯错的成本。在竞争激烈的互联网时代,试错当然是好事,但了解错误成本,避免不应该犯的错误&…...
)
谈谈一个程序员的职场心得(真有用)
谈谈一个程序员的职场心得 我会分为三个部分:软件开发,职场协作和认知成长,每个部分精简成 7 条心得。 软件开发 若无必要,勿增实体。 这是奥卡姆剃刀的定义,所谓剃刀就是法则,是奥卡姆这个英国学者提出来…...

Pytest:一个卓有成效的测试工具
大家都知道,目前最流行的Python单元测试框架有三种,分别是unittest, nose和pytest。其中unittest是Python自带的测试框架,但问题是比较老了,赶不上时代发展了(哈哈哈);nose2定位是带插件的unitt…...
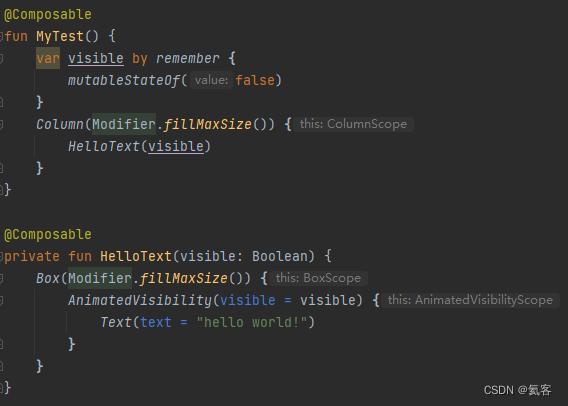
Compose 动画 (三) : AnimatedVisibility 从入门到深入
1. AnimatedVisibility 是什么 AnimatedVisibility可以实现Compose组件的显示和隐藏,并且可以指定显示/隐藏时候的动画效果。(EnterTransition/ExitTransition) 和 animateXxxAsState、animateContentSize、Crossfade、AnimatedContent 这几个API一起,都…...
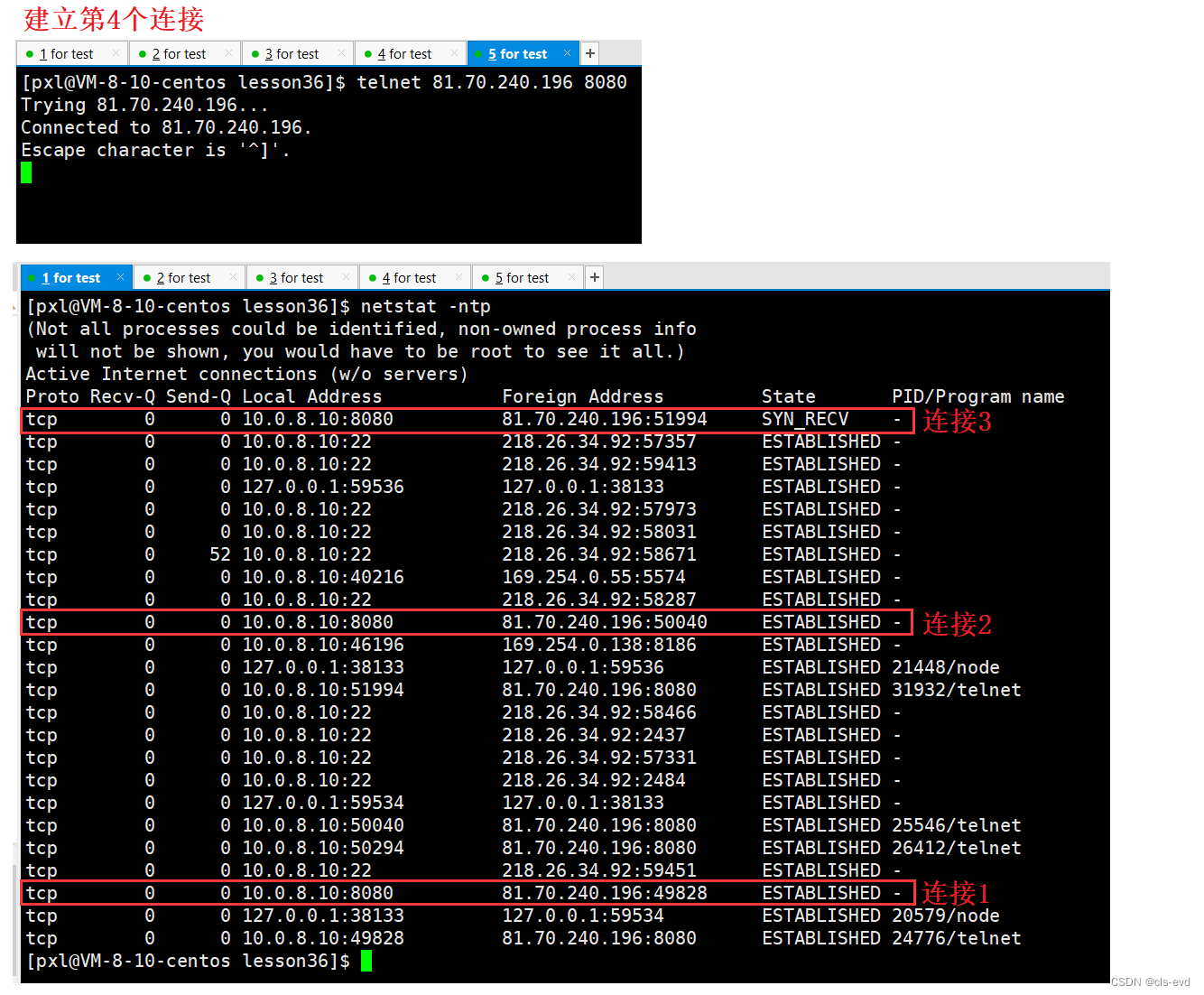
网络基础(二)
目录 应用层 再谈 "协议" 协议是一种 "约定". socket api的接口, 在读写数据时, 都是按 "字符串" 的方式来发送接收的. 如果我们要传输一些"结构化的数据" 怎么办呢? 为什么要转换呢? 如果我们将struct message里面…...
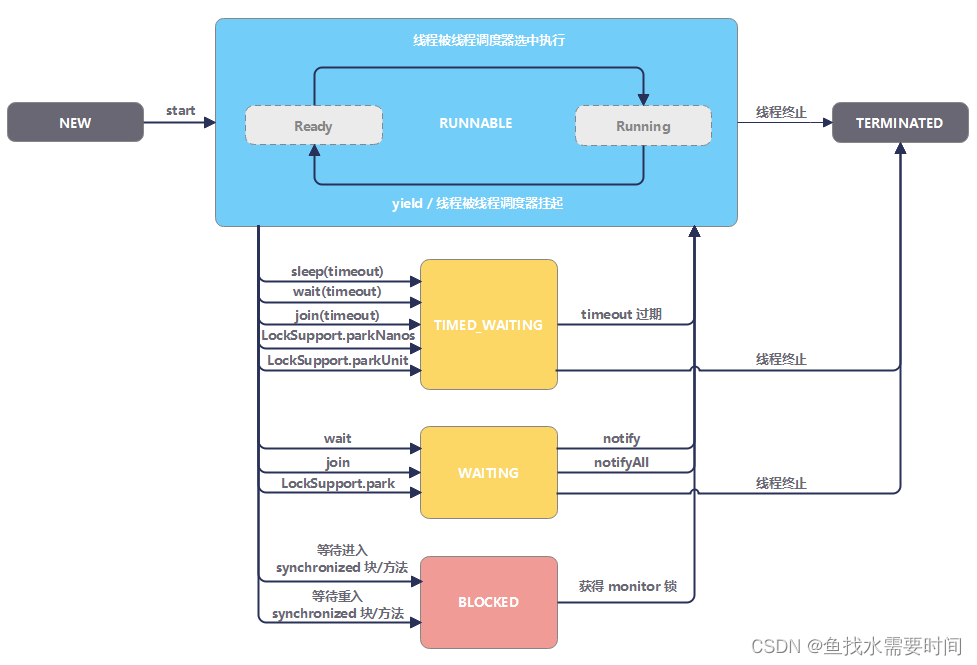
Java线程知识点总结
文章目录Java 线程基础线程简介什么是进程什么是线程进程和线程的区别创建线程ThreadRunnableCallable、Future、FutureTaskCallableFutureFutureTaskCallable Future FutureTask 示例线程基本用法线程休眠线程礼让终止线程守护线程线程通信wait/notify/notifyAlljoin管道线程…...
)
数据结构——第三章 栈与队列(4)
队列的应用1.基于队列的医院挂号模拟系统2.队列的运用1.基于队列的医院挂号模拟系统 代码实现分享 2.队列的运用 问题描述:某运动会设立N个比赛项目,每个运动成员可以参加1~3个项目。试问如何安排比赛日程,既可以使同一运动员参加的项目不…...

华为机试HJ73-计算日期到天数转换
HJ73 计算日期到天数转换 题目描述: 描述 根据输入的日期,计算是这一年的第几天。 保证年份为4位数且日期合法。 进阶:时间复杂度:O(n) ,空间复杂度:O(1) 输入描述: 输入一行,每行…...

【阅读笔记】你不知道的JavaScript--this与对象2
目录this默认绑定隐式绑定隐式丢失显示绑定API 调用上下文new 绑定this 绑定优先级其余绑定例外对象字面量与对象属性描述符迭代器遍历this 默认绑定 默认绑定适配 独立函数调用 默认绑定 this 指向全局对象; 故直接调用函数,该函数内部的 this 即指向全…...
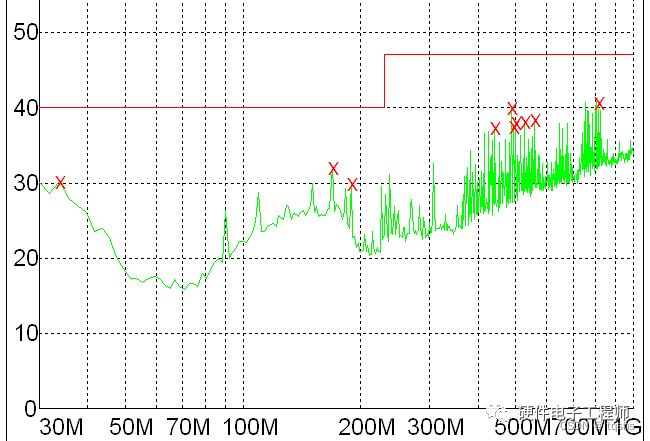
单板TVS接地不当造成辐射骚扰超标问题分析-EMC
【摘要】 某产品EMC辐射骚扰测试超标,通过近远场扫描配合定位分析,逐步找出骚扰源、传播路径,最终通过修改 PCB 走线切断传播路径解决此问题。 1 故障现象 某产品在进行 EMC 研发摸底测试时发现,整机辐射骚扰垂直方向测试超标&a…...
用Python Flask为女朋友做一个简单的网站(附可运行的源码)
🌟所属专栏:献给榕榕🐔作者简介:rchjr——五带信管菜只因一枚😮前言:该专栏系为女友准备的,里面会不定时发一些讨好她的技术作品,感兴趣的小伙伴可以关注一下~👉文章简介…...
vue3+rust个人博客建站日记5-所有界面
没有数据的前端,是没有灵魂的。明明标题是vue3 rust ,但日记撰写至今,似乎只有第一篇提及了Rust,这可不行。是时候一股作气,完成大部分页面绘制工作了! 最后再说一次,时间要加速了。 ——普奇神…...
)
青少年软件编程C++一级真题(202212)
1、输入一个整数x,输出这个整数加1后的值,即x1的值。 时间限制:1000 内存限制:65536 输入 一个整数x(0 ≤ x ≤ 1000)。 输出 按题目要求输出一个整数。 样例输入 9样例输出 10 #include<iost…...

【Spring】AOP底层原理(动态代理)-》 AOP概念及术语 -》 AOP实现
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ AOP - 面向切面编程一、简述AOP二、AOP底层原理…...
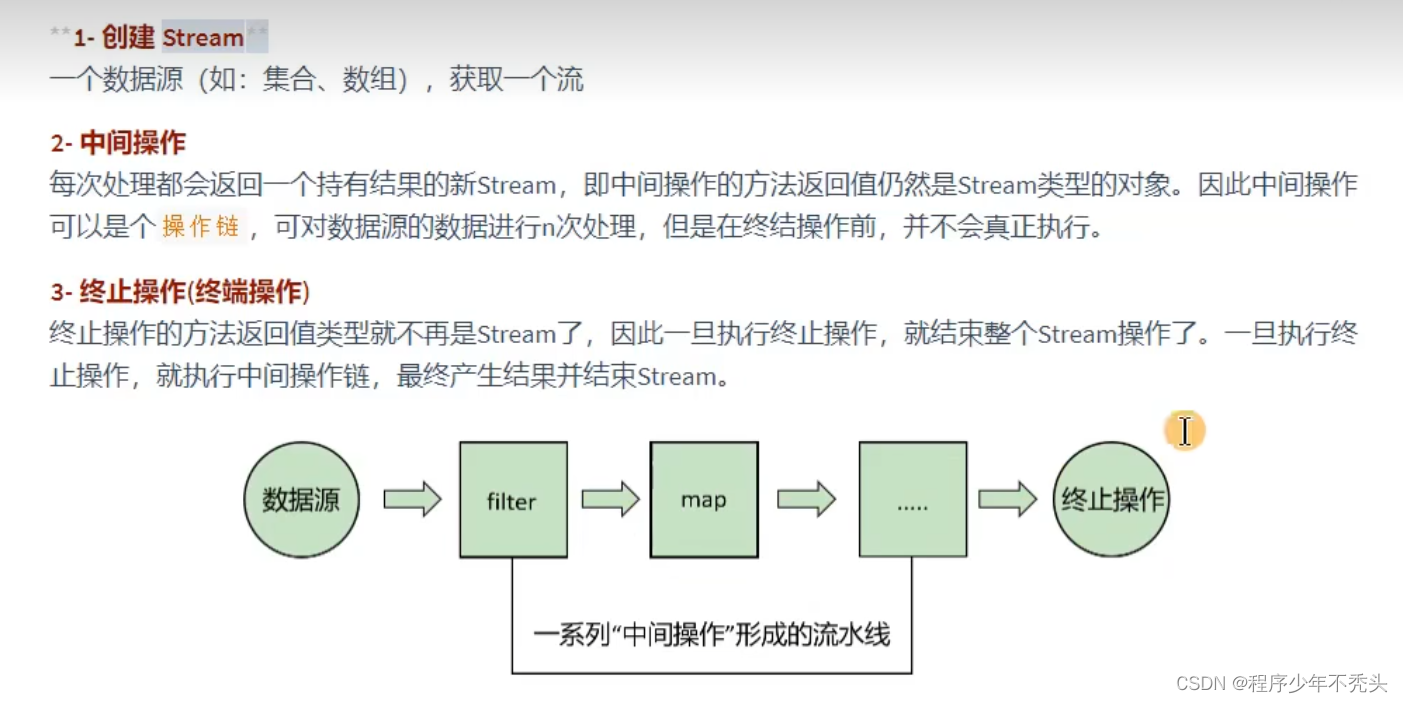
Java8 新特性 之 lambda 表达 和 函数式接口
—— lambda 表达式 概念 lambda 表达式是一个匿名函数,可以把 lambda 表达式理解为是一段可以传递的代码。更简洁、更灵活,使 Java 的语言表达能力得到了提升lambda 表达式是作为接口的实现类的对象(万事万物皆对象) 使用语法…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...
