【Day53】代码随想录之动态规划_买卖股票ⅠⅡ
文章目录
- 动态规划理论基础
- 动规五部曲:
- 出现结果不正确:
- 1. 买卖股票的最佳时机
- 2. 买卖股票的最佳时机Ⅱ
动态规划理论基础
动规五部曲:
- 确定dp数组 下标及dp[i] 的含义。
- 递推公式:比如斐波那契数列 dp[i] = dp[i-1] + dp[i-2]。
- 初始化dp数组。
- 确定遍历顺序:从前到后or其他。
- 打印。
出现结果不正确:
- 打印dp日志和自己想的一样:递推公式、初始化或者遍历顺序出错。
- 打印dp日志和自己想的不一样:代码实现细节出现问题。
1. 买卖股票的最佳时机
参考文档:代码随想录
分析:
买卖只有一次
dp五部曲:
- dp[i]含义:dp[i][0]表示持有i手里的现金,dp[i][1]表示不持有i手里的现金。
- 递推公式:dp[i][0] = max(dp[i-1][0], 0 - prices[i]); dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i]);
- 初始化:dp[0][0] = -prices[0]; dp[0][1] = 0;
- 遍历顺序:从小到大。
代码:
class Solution {
public:int maxProfit(vector<int>& prices) {//dp[i][0]:持有i股手里的钱//dp[i][1]:不持有i股手里的钱vector<vector<int>> dp(prices.size(), vector<int>(2,0));dp[0][0] = -prices[0];dp[0][1] = 0;for(int i = 1; i < prices.size(); i++){//第一次写的是:dp[i][0] = max(dp[i-1][0], dp[i-1][1]-prices[i])//但是股票只能买一次,所以当前的持有是 前一个的持有 和 现在买一个 的最大值dp[i][0] = max(dp[i-1][0], -prices[i]);dp[i][1] = max(dp[i-1][1], dp[i-1][0]+prices[i]);}return max(dp[prices.size()-1][0], dp[prices.size()-1][1]);}
};
2. 买卖股票的最佳时机Ⅱ
参考文档:代码随想录
分析:
买卖次数是不限的,之前有用贪心做过,这次用动态规划。
dp五部曲:
- dp[i]含义:dp[i][0]表示持有i手里的现金,dp[i][1]表示不持有i手里的现金。
- 递推公式:dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i]); dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i]);
- 初始化:dp[0][0] = -prices[0]; dp[0][1] = 0;
- 遍历顺序:从小到大。
代码:
class Solution {
public:int maxProfit(vector<int>& prices) {//dp[i][0]:i股持有手里的现金,i-1股也持有,i-1股不持有i股重新买入(设计多次买入和一次手中只有一股股票)//dp[i][1]:i股不持有手里的现金:i-1股也不持有,现金不变,i-1股持有i不持有卖出i-1买入i股vector<vector<int>> dp(prices.size(), vector<int>(2,0));dp[0][0] = -prices[0];dp[0][1] = 0;for(int i = 1; i < prices.size(); i++){dp[i][0] = max(dp[i-1][0], dp[i-1][1]-prices[i]);//i-1股持有,i股不持有,i股抛出,收益prices[i], dp[i-1][0]+prices[i]dp[i][1] = max(dp[i-1][1], dp[i-1][0]+prices[i]);}return max(dp[prices.size()-1][0], dp[prices.size()-1][1]);}
};
相关文章:

【Day53】代码随想录之动态规划_买卖股票ⅠⅡ
文章目录 动态规划理论基础动规五部曲:出现结果不正确: 1. 买卖股票的最佳时机2. 买卖股票的最佳时机Ⅱ 动态规划理论基础 动规五部曲: 确定dp数组 下标及dp[i] 的含义。递推公式:比如斐波那契数列 dp[i] dp[i-1] dp[i-2]。初…...
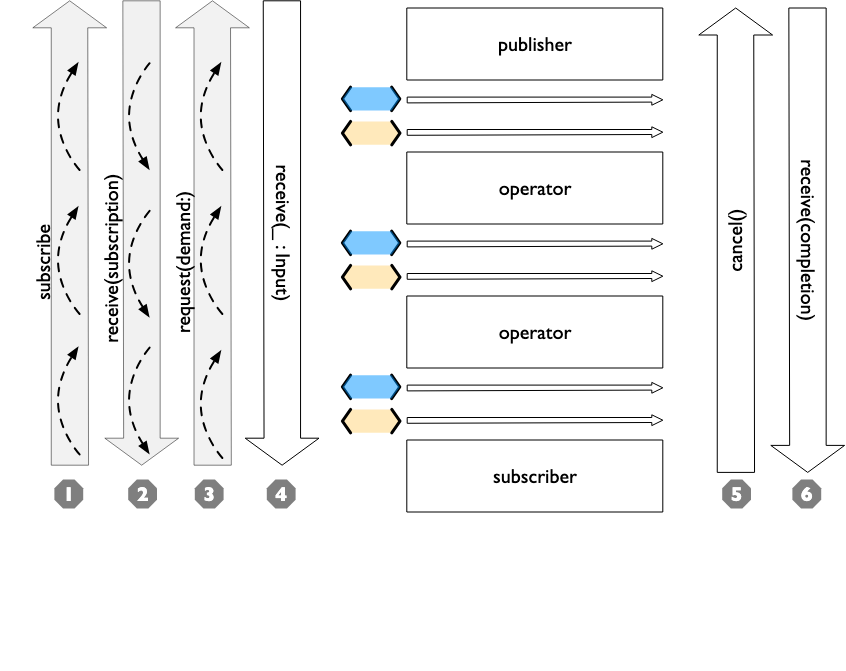
Swift Combine 使用调试器调试管道 从入门到精通二十六
Combine 系列 Swift Combine 从入门到精通一Swift Combine 发布者订阅者操作者 从入门到精通二Swift Combine 管道 从入门到精通三Swift Combine 发布者publisher的生命周期 从入门到精通四Swift Combine 操作符operations和Subjects发布者的生命周期 从入门到精通五Swift Com…...

go内置库函数实现client与server数据的发送接收
功能:客户端持续写入数据,直到输入exit退出,服务端读取数据并打印 注意:server和client目录在同一层级 服务端 server/main package mainimport ("fmt""net" )func main() {listen, err : net.Listen(&quo…...
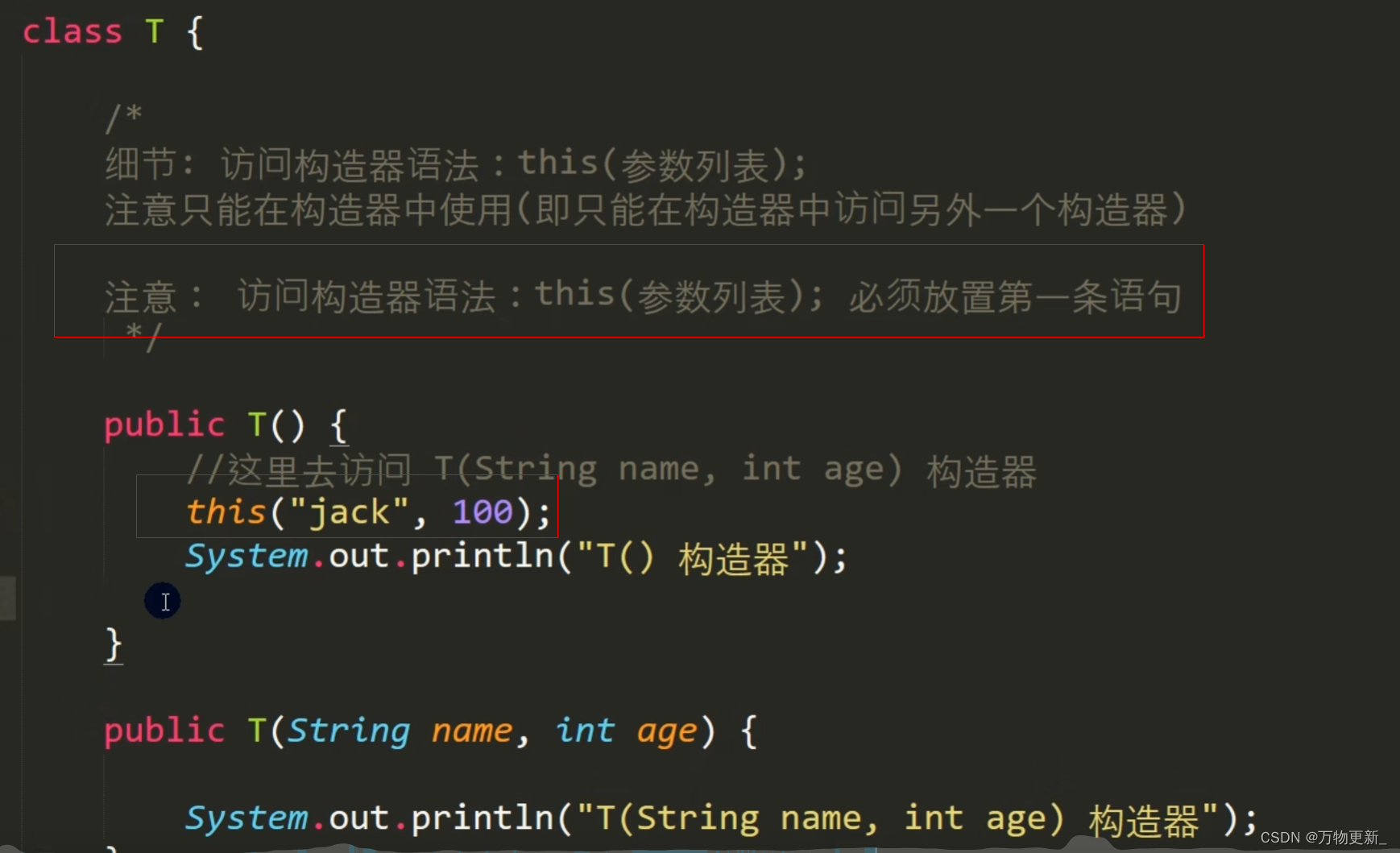
[java基础揉碎]this
引出this: 什么是this: java虚拟机会给每个对象分配 this,代表当前对象。 这里的this就是new出来的这个对象 this的本质: this是个引用在堆中指向它自己: this的细节: 访问成员方法: 访问构造器:...

vulnhub靶场之Deathnote
一.环境搭建 1.靶场描述 Level - easy Description : dont waste too much time thinking outside the box . It is a Straight forward box . This works better with VirtualBox rather than VMware 2.靶场下载 https://www.vulnhub.com/entry/deathnote-1,739/ 3.启动环…...

Docker安装Postgresql12
1、搜索仓库中postgres docker search postgres 2、拉取镜像 docker pull postgres docker pull postgres:12 #拉取12版本的PG库 3、创建数据库文件夹 cd /temp/ && mkdir -m 755 postgres-data 注:-m表示权限,类chmod命令 4、执行命令启动…...

服务器防火墙的应用技术有哪些类型?
随着互联网的发展,网络安全问题更加严峻。服务器防火墙技术作为一种基础的网络安全技术,对于保障我们的网络安全至关重要。本文将介绍服务器防火墙的概念和作用,以及主要的服务器防火墙技术,包括数据包过滤、状态检测、代理服务、…...

IP地理位置查询定位:技术原理与实际应用
在互联网时代,IP地址是连接世界的桥梁,而了解IP地址的地理位置对于网络管理、个性化服务以及安全监控都至关重要。IP数据云将深入探讨IP地理位置查询定位的技术原理、实际应用场景以及相关的隐私保护问题,旨在为读者提供全面了解和应用该技术…...

hbuilder运行不了php文件是什么原因?
如果 HBuilder 无法运行 PHP 文件,可能是由于以下几个常见原因导致的: 未安装 PHP 解释器: HBuilder 需要安装 PHP 解释器才能运行 PHP 文件。请确保您的系统中已经安装了 PHP,并且已正确配置了环境变量。 PHP 解释器路径错误&…...
)
C++从入门到精通 第十六章(STL常用算法)
写在前面: 本系列专栏主要介绍C的相关知识,思路以下面的参考链接教程为主,大部分笔记也出自该教程,笔者的原创部分主要在示例代码的注释部分。除了参考下面的链接教程以外,笔者还参考了其它的一些C教材(比…...
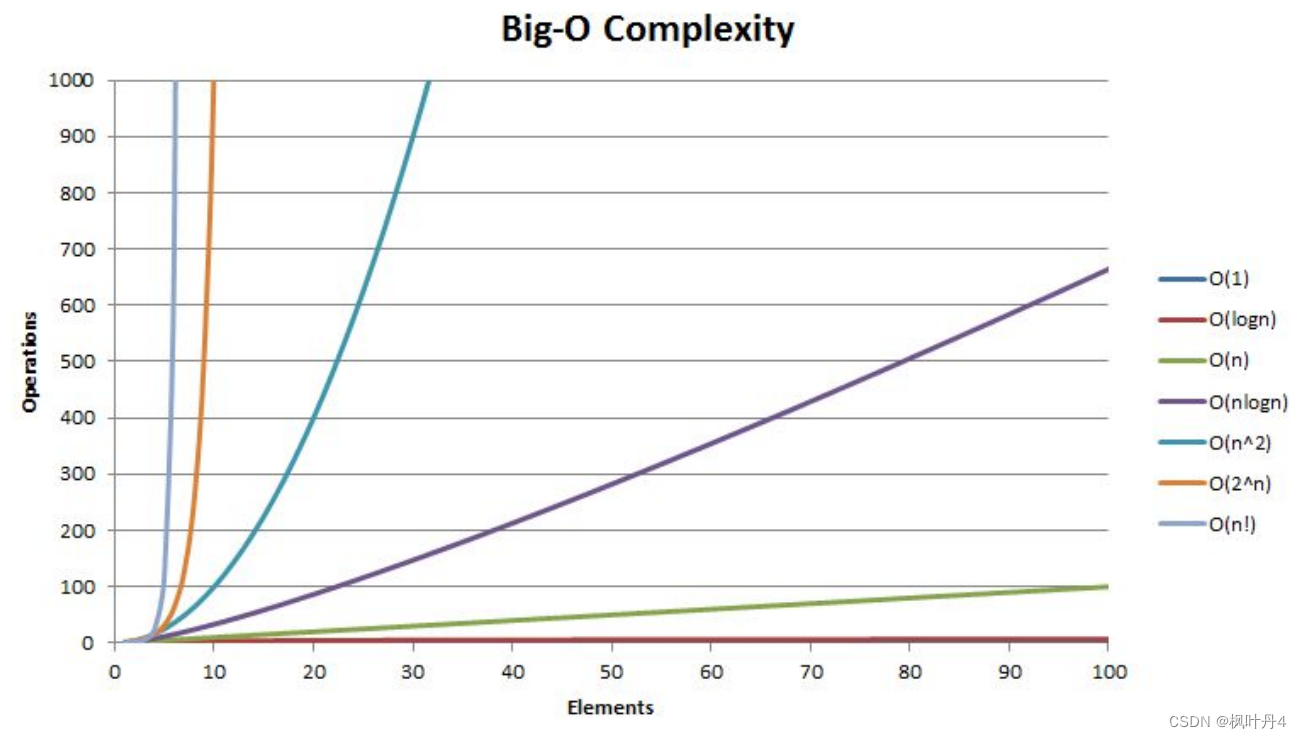
【海贼王的数据航海:利用数据结构成为数据海洋的霸主】时间复杂度 | 空间复杂度
目录 1 -> 算法效率 1.1 -> 如何衡量一个算法的好坏? 1.2 -> 算法的复杂度 2 -> 时间复杂度 2.1 -> 时间复杂度的概念 2.2 -> 大O的渐进表示法 2.3 -> 常见时间复杂度计算 3 -> 空间复杂度 4 -> 常见复杂度对比 1 -> 算法效…...

OpenTiny Vue 组件库适配微前端可能遇到的4个问题
本文由体验技术团队 TinyVue 项目成员岑灌铭同学创作。 前言 微前端是一种多个团队通过独立发布功能的方式来共同构建现代化 web 应用的技术手段及方法策略,每个应用可以选择不同的技术栈,独立开发、独立部署。 TinyVue组件库的跨技术栈能力与微前端十…...
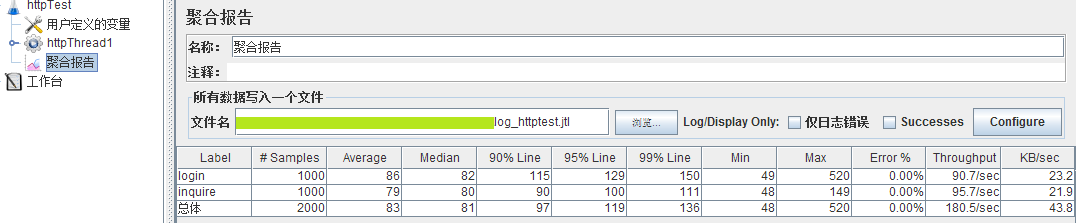
jmeter 命令行启动 动态参数化
[Jmeter命令行参数] 一、在linux中,使用非gui的方式执行jmeter。若需更改参数,必须先编辑jmx文件,找到对应的变量进行修改,比较麻烦。因此,可以参数化一些常用的变量,直接在Jmeter命令行进行设置 二、参数…...

C++跨模块释放内存
linux一个进程只有一个堆,不要考虑这些问题,但是windows一个进程可能有多个堆,要在对应的堆上释放。 一, MT改MD 一个进程的地址空间是由一个可执行模块和多个DLL模块构成的,这些模块中,有些可能会链接到…...

jQuery浅析
jQuery 是一个快速、简洁的 JavaScript 库,旨在简化 HTML 文档遍历、事件处理、动画以及 Ajax 交互等功能。由 John Resig 在2006年创建,它极大地简化了JavaScript开发人员在处理网页文档、选择DOM元素以及执行各种效果和功能时的工作。 核心特性&#x…...
)
分班问题 、幼儿园分班(C语言)
题目 幼儿园两个班的小朋友排队时混在了一起,每个小朋友都知道自己跟前面一个小朋友是不是同班,请你帮忙把同班的小朋友找出来 小朋友的编号为整数,与前面一个小朋友同班用Y表示,不同班用N表示 输入 输入为空格分开的小朋友编号…...

QT 如何让多语言翻译变得简单,提高效率?
一.QT多语言如何翻译的? 在QT的多语言翻译过程中,分为两个步骤:第一步生成ts文件,第二步将ts文件翻译为qm文件。如果我们在需要多语言的情况下,qml经常使用qstr或者qwidget中使用tr等等,遍布许多个文件夹,在需要更新新的翻译时会很麻烦。整个工程收索并修改,效率十分低…...

线性代数:线性方程组解的结构
目录 齐次/非齐次方程组的解 Ax 0 的解的性质 定理 Ax b 的解的性质 相关证明 例1 例2 例3 齐次/非齐次方程组的解 Ax 0 的解的性质 定理 Ax b 的解的性质 相关证明 例1 例2 例3...

mysql之CRUD常见函数union查询
select select * from c insert 字段设置自增后,当我们指定增加一条数据后,往后增加的数据都会在该条数据后进行递增,但是可以认为的指定增加某条id不存在的数据 insert into c values(7,‘政治’) insert into c(c2) values(‘历史1’),(…...

开窗函数实践-实现两行记录之间计算时间差
一、需求背景 基于保密要求,不放原始表,新建测试表用来演示 insert into TEST0221 (采血人, 采血时间, 条码号, 病人ID) values (张三, to_date(21-02-2024 12:00:00, dd-mm-yyyy hh24:mi:ss), 2024001, 0001);insert into TEST0221 (采血人, 采血时间…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
