vue3 #跨组件通信
//爷爷组件中
import { provide , ref } from 'vue'
const money = ref (100) //定义数据
provide( 'money' , money ) //提供数据给孙子组件
const changeMoney = ( m:number ) => { //定义函数
if (money) {
money.value = money.value - m
}
}
provide("changeMoney ",changeMoney) //提供函数给孙子组件
// 孙子组件中
import { inject } from 'vue'
const money = inject('money') //获取传递过来的数据
const changeMoney = inject<m:number> => viod ('changeMoney ') //获取传递过来的函数
举例:如果在孙子组件中想要修改爷爷组件的数据
// 孙子组件中
<button @click="handleMoney">
import { inject } from 'vue'
const money = inject< Ref<number> >('money') //获取数据
const handleMoney=()=> {
if(money) { //在跨组件通信中,可能没有传值,所有这里做一个判断
money.value += 2
}
}
⭐inject函数会默认将数据定义为unknown,所以这里需要定义一下传过来数据的类型
相关文章:

vue3 #跨组件通信
//爷爷组件中 import { provide , ref } from vue const money ref (100) //定义数据 provide( money , money ) //提供数据给孙子组件 const changeMoney ( m:number ) > { //定义函数 if (money) { money.value money.value - m } } provide(&quo…...

【AI绘画工具有哪些?】讲解
AI绘画工具有哪些? AI绘画工具有哪些? AI绘画工具有哪些? 截至现在,有多种AI绘画工具被广泛使用。以下是一些流行的AI画图工具和平台: 1. DeepArt - 利用神经网络将你的照片转换成类似著名画家作品的艺术作品。 2. …...

在Vue中使用TypeScript时 props指定枚举类型
推荐一款AI网站 AI写作与AI绘画智能创作平台 - 海鲸AI | 智能AI助手,可以免费领取GPT3.5无限卡 在Vue中使用TypeScript时,您可以通过定义一个枚举类型,然后在组件的props定义中使用这个枚举来指定props的类型。以下是一个如何做到这一点的例子…...

快速将excel/word表格转换为web页面(html)的方法
前言 在进行开发企业信息化建设的过程,应该有很多这样的场景,就是将现有的电子表格记录的方式转换为在数据系统中进行网页上报。也就是需要根据当前一直使用的表格制作一个上传这个表格信息的网页,如果要减少系统的使用学习成本,…...

想高薪就业鸿蒙HarmonyOS 开发岗位,到底该学习些啥?
鸿蒙是什么? 经过十多年的发展,传统移动互联网的增长红利已渐见顶。万物互联时代正在开启,应用的设备底座将从几十亿手机扩展到数百亿 IoT 设备。GSMA 预测到 2025 年,全球物联网终端连接数量将达 246 亿个,其中消费物…...

Java中的建造者模式
建造者模式(Builder Pattern)是一种创建型设计模式,用于创建复杂对象。它将对象的创建过程分离出来,使得构建过程可以独立于对象本身的表示和组成。 在Java中,建造者模式的实现通常涉及以下几个角色: Prod…...

机器学习面试:逻辑回归与朴素贝叶斯区别
逻辑回归与朴素贝叶斯区别有以下几个方面: (1)逻辑回归是判别模型,朴素贝叶斯是生成模型,所以生成和判别的所有区别它们都有。 (2)朴素贝叶斯属于贝叶斯,逻辑回归是最大似然,两种概率哲学间的区别。 (3)朴素贝叶斯需要条件独立假设…...

数据结构之线性表
线性表 数据结构之线性表一、基本定义1、线性表的概念、定义,特点,线性表抽象数据类型定义2、其他 二、线性表的顺序表示与实现1、静态顺序表2、静态表 三、线性表的链式表示与实现1、单链表包含了指针的知识,是第一部分的重难点2、特点3、代…...

记录解决uniapp使用uview-plus在vue3+vite+ts项目中打包后样式不能显示问题
一、背景 从 vue2+uview1 升级到 vue3+vite+ts+uview-plus ,uview组件样式打包后不显示,升级前uview 组件是可以正常显示,升级后本地运行是可以正常显示,但是打包发布成H5后uview的组件无法正常显示,其他uniapp自己的组件可以正常显示。折腾了很久,这里记录下我是如何解决…...

三年功能测试,测试工作吐槽
概述 大家好,我是洋子。有很多粉丝朋友目前还是在做功能测试,日常会遇到很多繁琐,棘手的问题,今天分享一篇在testerhome社区的帖子《三年功能测试,测试工作吐槽》 原文链接https://testerhome.com/topics/38546 这篇文…...
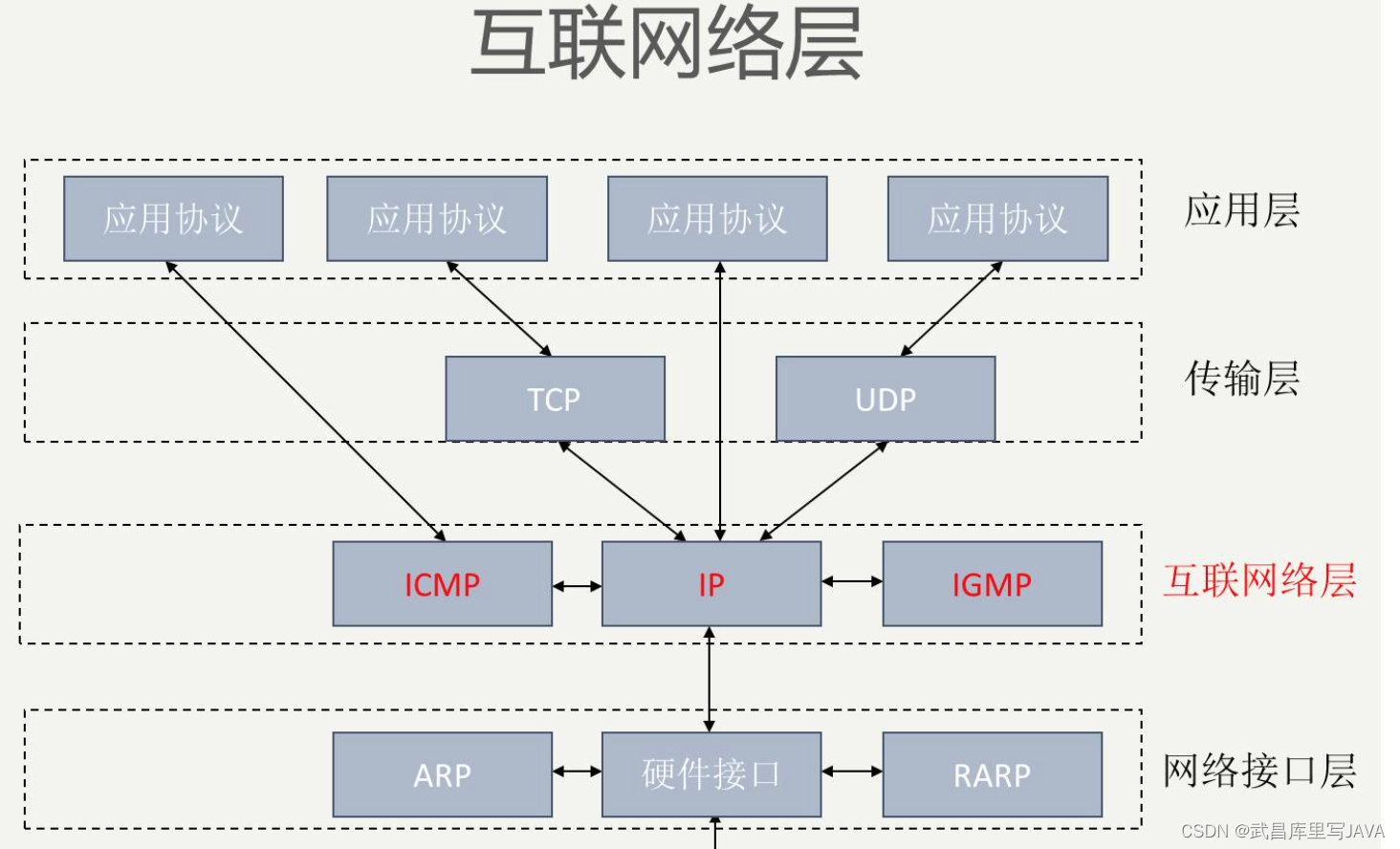
0206-1-网络层
第 4 章 网络层 网络层提供的两种服务 虚电路服务 数据报服务 概要: 虚电路服务与数据报服务的对比 网际协议 IP 网际协议 IP 是 TCP/IP 体系中两个最主要的协议之一。与 IP 协议配套使用的还有四个协议: 地址解析协议 ARP (Address Resolution Protocol)逆地…...
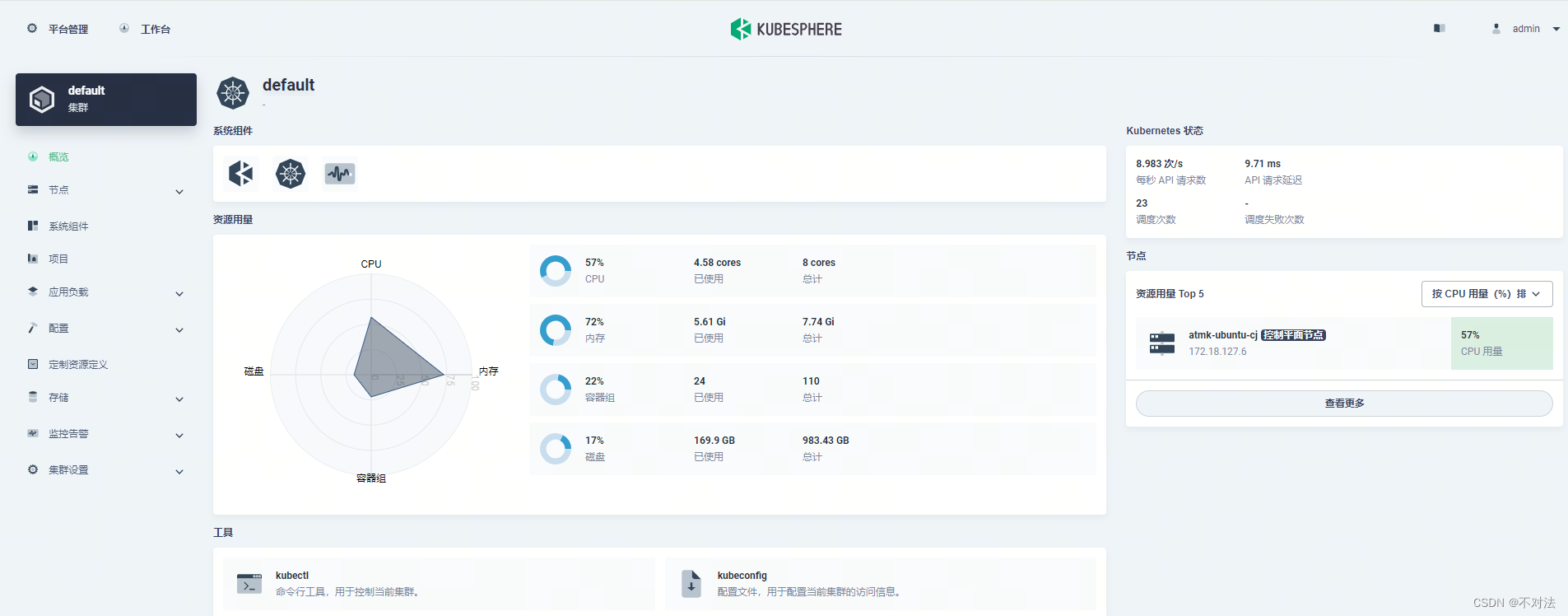
以 All-in-One 模式安装 KubeSphere时避坑
环境 ubuntu 18.04 准备 安装服务插件 socat 必须 可选但建议 conntrack 必须 可选但建议 ebtables 可选但建议 可选但建议 ipset 可选但建议 可选但建议 命令 sudo apt-get install socat安装docker 建议自行安装,不用KubeSphere 自带的 处理服务器配置 1…...
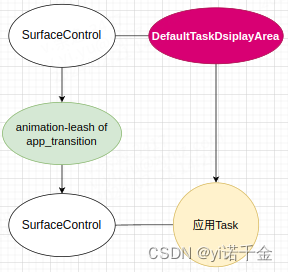
Android T 远程动画显示流程其二——动画的添加流程(更新中)
前言 接着上篇文章分析 Android T 远程动画显示流程其一 切入点——处理应用的显示过渡 下面,我们以从桌面点击一个应用启动的场景来分析远程动画的流程,窗口添加的流程见Android T WMS窗口相关流程 这里我们从AppTransitionController.handleAppTran…...

Pytorch-SGD算法解析
关注B站可以观看更多实战教学视频:肆十二-的个人空间-肆十二-个人主页-哔哩哔哩视频 (bilibili.com) SGD,即随机梯度下降(Stochastic Gradient Descent),是机器学习中用于优化目标函数的迭代方法,特别是在处…...

物联网土壤传感器简介
物联网土壤传感器简介 物联网土壤传感器的工作原理基于多种物理、化学和生物原理,通过感应器等组成部件将土壤中的特征数据转化为电信号,从而进行采集、处理和输出。这些传感器主要包括土壤湿度传感器、土壤温度传感器、土壤酸碱度传感器和土壤颗粒物传…...
)
MySQL索引面试题(高频)
文章目录 前言什么时候需要(不需要))使用索引?有哪些优化索引的方法前缀索引优化索引覆盖优化索引失效场景 总结 前言 今天来讲一讲 MySQL 索引的高频面试题。主要是针对前一篇文章 MySQL索引入门(一文搞定)进行查漏补…...

SouthLeetCode-打卡24年02月第2周
SouthLeetCode-打卡24年02月第2周 // Date : 2024/02/05 ~ 2024/02/11 039.有效的字母异位词 (1) 题目描述 039#LeetCode.242.简单题目链接#Monday2024/02/05 给定两个字符串 *s* 和 *t* ,编写一个函数来判断 *t* 是否是 *s* 的字母异位词。 **注意࿱…...

Rust CallBack的几种写法
模拟常用的几种函数调用CallBack的写法。测试调用都放在函数t6_call_back_task中。我正在学习Rust,有不对或者欠缺的地方,欢迎交流指正 type Callback std::sync::Arc<dyn Fn() Send Sync>; type CallbackReturnVal std::sync::Arc<dyn Fn…...

Redis突现拒绝连接问题处理总结
一、问题回顾 项目突然报异常 [INFO] 2024-02-20 10:09:43.116 i.l.core.protocol.ConnectionWatchdog [171]: Reconnecting, last destination was 192.168.0.231:6379 [WARN] 2024-02-20 10:09:43.120 i.l.core.protocol.ConnectionWatchdog [151]: Cannot reconnect…...

css中选择器的优先级
CSS 的优先级是由选择器的特指度(Specificity)和重要性(Importance)决定的,以下是优先级规则: 特指度: ID 选择器 (#id): 每个ID选择器计为100。 类选择器 (.class)、属性选择器 ([attr]) 和伪…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...
