Pytorch-SGD算法解析
关注B站可以观看更多实战教学视频:肆十二-的个人空间-肆十二-个人主页-哔哩哔哩视频 (bilibili.com)
SGD,即随机梯度下降(Stochastic Gradient Descent),是机器学习中用于优化目标函数的迭代方法,特别是在处理大数据集和在线学习场景中。与传统的批量梯度下降(Batch Gradient Descent)不同,SGD在每一步中仅使用一个样本来计算梯度并更新模型参数,这使得它在处理大规模数据集时更加高效。
SGD算法的基本步骤
- 初始化参数:选择初始参数值,可以是随机的或者基于一些先验知识。
- 随机选择样本:从数据集中随机选择一个样本。
- 计算梯度:计算损失函数关于当前参数的梯度。
- 更新参数:沿着负梯度方向更新参数。
- 重复:重复步骤2-4,直到满足停止条件(如达到预设的迭代次数或损失函数的改变小于某个阈值)。
SGD的Python代码示例:
python实现
假设我们要使用SGD来优化一个简单的线性回归模型。
import numpy as np # 目标函数(损失函数)和其梯度
def loss_function(w, b, x, y): return np.sum((y - (w * x + b)) ** 2) / len(x) def gradient_function(w, b, x, y): dw = -2 * np.sum((y - (w * x + b)) * x) / len(x) db = -2 * np.sum(y - (w * x + b)) / len(x) return dw, db # SGD算法
def sgd(x, y, learning_rate=0.01, epochs=1000): # 初始化参数 w = np.random.rand() b = np.random.rand() # 存储每次迭代的损失值,用于可视化 losses = [] for i in range(epochs): # 随机选择一个样本(在这个示例中,我们没有实际进行随机选择,而是使用了整个数据集。在大数据集上,你应该随机选择一个样本或小批量样本。) # 注意:为了简化示例,这里我们实际上使用的是批量梯度下降。在真正的SGD中,你应该在这里随机选择一个样本。 # 计算梯度 dw, db = gradient_function(w, b, x, y) # 更新参数 w = w - learning_rate * dw b = b - learning_rate * db # 记录损失值 loss = loss_function(w, b, x, y) losses.append(loss) # 每隔一段时间打印损失值(可选) if i % 100 == 0: print(f"Epoch {i}, Loss: {loss}") return w, b, losses # 示例数据(你可以替换为自己的数据)
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 6, 8, 10]) # 运行SGD算法
w, b, losses = sgd(x, y)
print(f"Optimized parameters: w = {w}, b = {b}")
解析
- 在上面的代码中,我们首先定义了损失函数和它的梯度。对于线性回归,损失函数通常是均方误差。
sgd函数实现了SGD算法。它接受输入数据x和标签y,以及学习率和迭代次数作为参数。- 在每次迭代中,我们计算损失函数关于参数
w和b的梯度,并使用这些梯度来更新参数。 - 我们还记录了每次迭代的损失值,以便稍后可视化算法的收敛情况。
- 最后,我们打印出优化后的参数值。在实际应用中,你可能还需要使用这些参数来对新数据进行预测。
在PyTorch中,SGD(随机梯度下降)是一种基本的优化器,用于调整模型的参数以最小化损失函数。下面是torch.optim.SGD的参数解析和一个简单的用例。
SGD的Pytorch代码示例:
参数解析
torch.optim.SGD的主要参数如下:
- params (iterable):待优化的参数,或者是定义了参数的模型的迭代器。
- lr (float):学习率。这是更新参数的步长大小。较小的值会导致更新更精细,而较大的值可能会导致训练过程不稳定。这是SGD优化器的一个关键参数。
- momentum (float, optional):动量因子 (default: 0)。该参数加速了SGD在相关方向上的收敛,并抑制了震荡。
- dampening (float, optional):动量的抑制因子 (default: 0)。增加此值可以减少动量的影响。在实际应用中,这个参数的使用较少。
- weight_decay (float, optional):权重衰减 (L2 penalty) (default: 0)。通过向损失函数添加与权重向量平方成比例的惩罚项,来防止过拟合。
- nesterov (bool, optional):是否使用Nesterov动量 (default: False)。Nesterov动量是标准动量方法的一个变种,它在计算梯度时使用了未来的近似位置。
用例
下面是一个使用SGD优化器的简单例子:
import torch
import torch.nn as nn
import torch.optim as optim # 定义一个简单的模型
model = nn.Sequential( nn.Linear(10, 5), nn.ReLU(), nn.Linear(5, 2),
) # 定义损失函数
criterion = nn.CrossEntropyLoss() # 定义优化器
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9, weight_decay=0.001) # 假设有输入数据和目标
input_data = torch.randn(1, 10)
target = torch.tensor([1]) # 训练循环(这里只展示了一次迭代)
for epoch in range(1): # 通常会有多个 epochs # 前向传播 output = model(input_data) # 计算损失 loss = criterion(output, target) # 反向传播 optimizer.zero_grad() # 清除之前的梯度 loss.backward() # 计算当前梯度 # 更新参数 optimizer.step() # 应用梯度更新 # 打印损失 print(f'Epoch {epoch+1}, Loss: {loss.item()}')
在这个例子中,我们创建了一个简单的两层神经网络模型,并使用SGD优化器来更新模型的参数。在训练循环中,我们执行了前向传播来计算模型的输出,然后计算了损失,通过调用loss.backward()执行了反向传播来计算梯度,最后通过调用optimizer.step()更新了模型的参数。在每次迭代开始时,我们使用optimizer.zero_grad()来清除之前累积的梯度,这是非常重要的步骤,因为PyTorch默认会累积梯度。
相关文章:

Pytorch-SGD算法解析
关注B站可以观看更多实战教学视频:肆十二-的个人空间-肆十二-个人主页-哔哩哔哩视频 (bilibili.com) SGD,即随机梯度下降(Stochastic Gradient Descent),是机器学习中用于优化目标函数的迭代方法,特别是在处…...

物联网土壤传感器简介
物联网土壤传感器简介 物联网土壤传感器的工作原理基于多种物理、化学和生物原理,通过感应器等组成部件将土壤中的特征数据转化为电信号,从而进行采集、处理和输出。这些传感器主要包括土壤湿度传感器、土壤温度传感器、土壤酸碱度传感器和土壤颗粒物传…...
)
MySQL索引面试题(高频)
文章目录 前言什么时候需要(不需要))使用索引?有哪些优化索引的方法前缀索引优化索引覆盖优化索引失效场景 总结 前言 今天来讲一讲 MySQL 索引的高频面试题。主要是针对前一篇文章 MySQL索引入门(一文搞定)进行查漏补…...

SouthLeetCode-打卡24年02月第2周
SouthLeetCode-打卡24年02月第2周 // Date : 2024/02/05 ~ 2024/02/11 039.有效的字母异位词 (1) 题目描述 039#LeetCode.242.简单题目链接#Monday2024/02/05 给定两个字符串 *s* 和 *t* ,编写一个函数来判断 *t* 是否是 *s* 的字母异位词。 **注意࿱…...

Rust CallBack的几种写法
模拟常用的几种函数调用CallBack的写法。测试调用都放在函数t6_call_back_task中。我正在学习Rust,有不对或者欠缺的地方,欢迎交流指正 type Callback std::sync::Arc<dyn Fn() Send Sync>; type CallbackReturnVal std::sync::Arc<dyn Fn…...

Redis突现拒绝连接问题处理总结
一、问题回顾 项目突然报异常 [INFO] 2024-02-20 10:09:43.116 i.l.core.protocol.ConnectionWatchdog [171]: Reconnecting, last destination was 192.168.0.231:6379 [WARN] 2024-02-20 10:09:43.120 i.l.core.protocol.ConnectionWatchdog [151]: Cannot reconnect…...

css中选择器的优先级
CSS 的优先级是由选择器的特指度(Specificity)和重要性(Importance)决定的,以下是优先级规则: 特指度: ID 选择器 (#id): 每个ID选择器计为100。 类选择器 (.class)、属性选择器 ([attr]) 和伪…...
心得)
python3字符串内建方法split()心得
python3字符串内建方法split()心得 概念 用指定分隔符(默认是任何空白字符)将字符串拆分成列表。 语法 string.split(separator.max) 参数1.split(参数2,参数3) 参数1:string 字符串,需要被拆分的字符串。 参数2&a…...

html的列表标签
列表标签 列表在html里面经常会用到的,主要使用来布局的,使其整齐好看. 无序列表 无序列表[重要]: ul ,li 示例代码1: 对应的效果: 无序列表的属性 属性值描述typedisc,square,…...
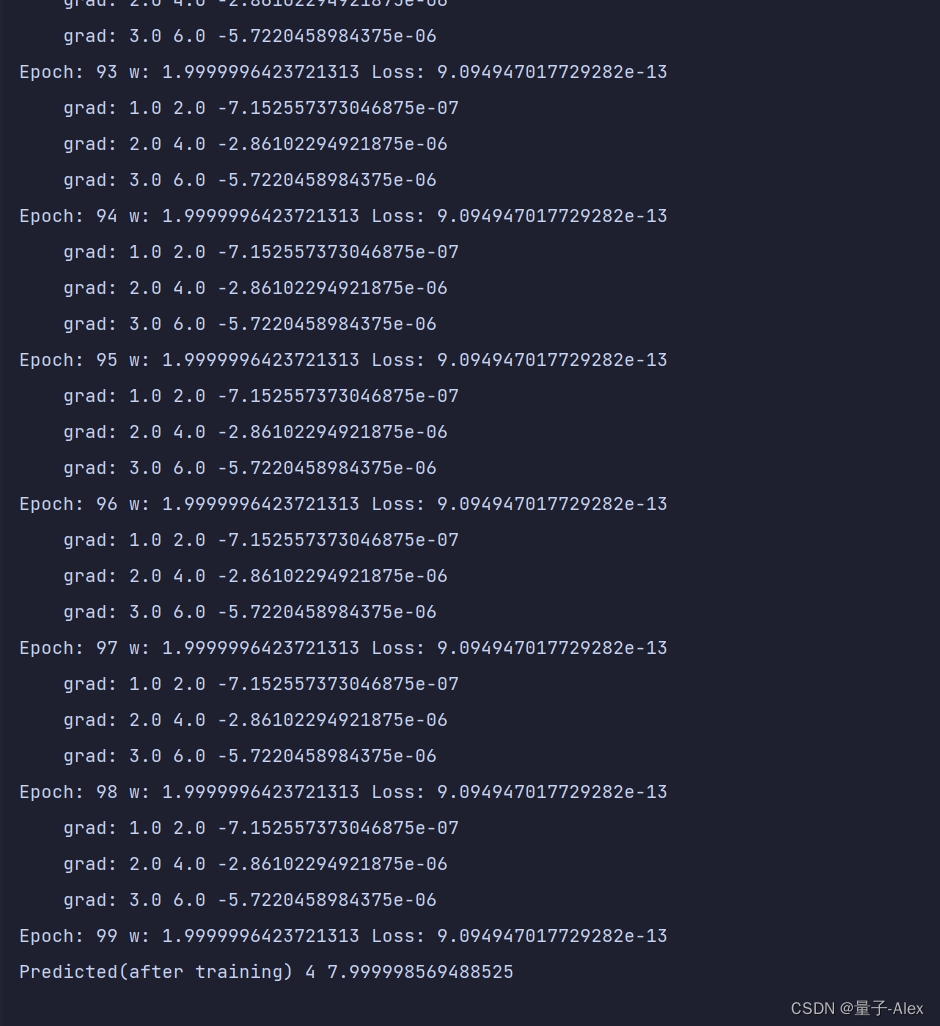
【Pytorch深度学习开发实践学习】B站刘二大人课程笔记整理lecture04反向传播
lecture04反向传播 课程网址 Pytorch深度学习实践 部分课件内容: import torchx_data [1.0,2.0,3.0] y_data [2.0,4.0,6.0] w torch.tensor([1.0]) w.requires_grad Truedef forward(x):return x*wdef loss(x,y):y_pred forward(x)return (y_pred-y)**2…...
PyTorch使用Tricks:学习率衰减 !!
文章目录 前言 1、指数衰减 2、固定步长衰减 3、多步长衰减 4、余弦退火衰减 5、自适应学习率衰减 6、自定义函数实现学习率调整:不同层不同的学习率 前言 在训练神经网络时,如果学习率过大,优化算法可能会在最优解附近震荡而无法收敛&#x…...
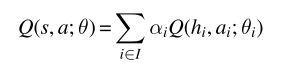
10MARL深度强化学习 Value Decomposition in Common-Reward Games
文章目录 前言1、价值分解的研究现状2、Individual-Global-Max Property3、Linear and Monotonic Value Decomposition3.1线性值分解3.2 单调值分解 前言 中心化价值函数能够缓解一些多智能体强化学习当中的问题,如非平稳性、局部可观测、信用分配与均衡选择等问题…...

2 Nacos适配达梦数据库实现方案
1、修改源代码方式 Nacos 原生是不支持达梦数据库的,所以就要想办法让它 “支持”,因为是开源软件,我们可以从源码入手,在流行的 1.x 、2.x 或最新版本代码的基本上进行修改。 主要涉及到以下内容的修改: com/alibaba/nacos/persistence/datasource/ExternalDataS...
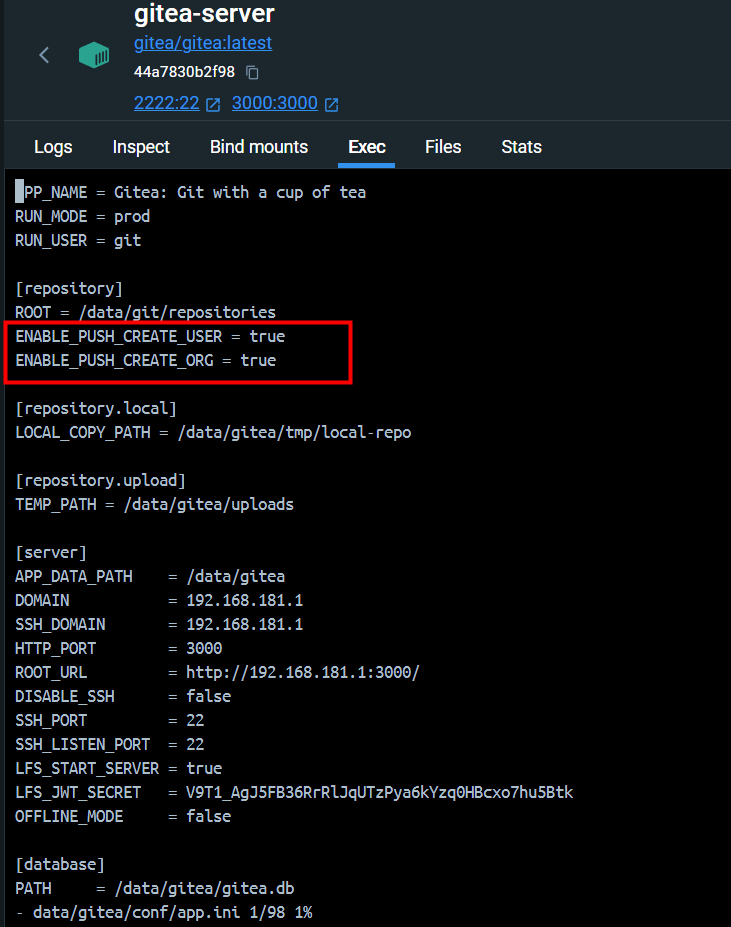
【Gitea】配置 Push To Create
引 在 Git 代码管理工具使用过程中,经常需要将一个文件夹作为仓库上传到一个未创建的代码仓库。如果 Git 服务端使用的是 Gitea,通常会推送失败。 PS D:\tmp\git-test> git remote add origin http://192.1.1.1:3000/root/git-test.git PS D:\tmp\g…...
)
关于postgresql数据库单独设置某个用户日志级别(日志审计)
前言: 很多时候我们想让数据库日志打印详细一点,但是又担心会对数据库本身产生一些不可控的影响,还会担心数据库产生的庞大的日志导致主机资源不太够用的影响。那么今天我们就通过讲解给单个用户设置 log_statement来解决以上这些问题。 注…...
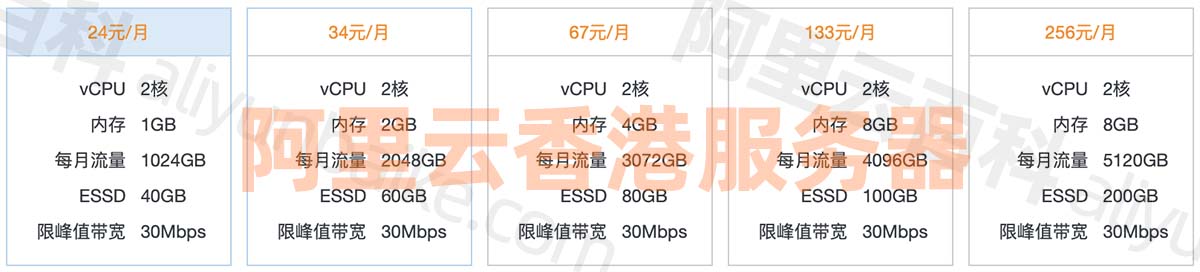
阿里云ECS香港服务器性能强大、cn2高速网络租用价格表
阿里云香港服务器中国香港数据中心网络线路类型BGP多线精品,中国电信CN2高速网络高质量、大规格BGP带宽,运营商精品公网直连中国内地,时延更低,优化海外回中国内地流量的公网线路,可以提高国际业务访问质量。阿里云服务…...
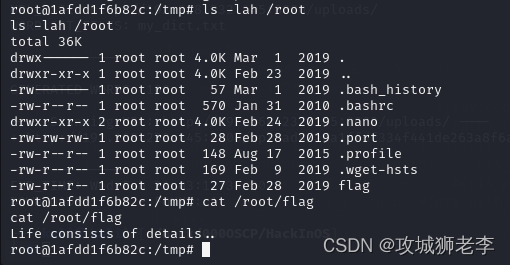
实战打靶集锦-025-HackInOS
文章目录 1. 主机发现2. 端口扫描3. 服务枚举4. 服务探查5. 提权5.1 枚举系统信息5.2 探索一下passwd5.3 枚举可执行文件5.4 查看capabilities位5.5 目录探索5.6 枚举定时任务5.7 Linpeas提权 靶机地址:https://download.vulnhub.com/hackinos/HackInOS.ova 1. 主机…...
.forEach()和list.forEach()的区别)
list.stream().forEach()和list.forEach()的区别
list.stream().forEach() 和 list.forEach() 在 Java 中都是用于遍历集合元素的方法,但它们在使用场景和功能上有所不同: list.forEach(): 是从 Java 8 开始引入到 java.util.List 接口的标准方法。直接对列表进行迭代,它采用内部…...
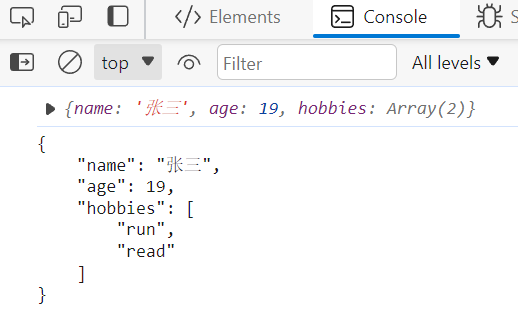
JS基础之JSON对象
JS基础之JSON对象 目录 JS基础之JSON对象对象转JSON字符串JSON转JS对象 对象转JSON字符串 JSON.stringify(value,replacer,space) value:要转换的JS对象 replacer:(可选)用于过滤和转换结果的函数或数组 space:(可选)指定缩进量 // 创建JS对象 let date {name:"张三…...
嵌入式学习之Linux入门篇——使用VMware创建Unbuntu虚拟机
目录 主机硬件要求 VMware 安装 安装Unbuntu 18.04.6 LTS 新建虚拟机 进入Unbuntu安装环节 主机硬件要求 内存最少16G 硬盘最好分出一个单独的盘,而且最少预留200G,可以使用移动固态操作系统win7/10/11 VMware 安装 版本:VMware Works…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
