10MARL深度强化学习 Value Decomposition in Common-Reward Games
文章目录
- 前言
- 1、价值分解的研究现状
- 2、Individual-Global-Max Property
- 3、Linear and Monotonic Value Decomposition
- 3.1线性值分解
- 3.2 单调值分解
前言
中心化价值函数能够缓解一些多智能体强化学习当中的问题,如非平稳性、局部可观测、信用分配与均衡选择等问题,然而存在很难直接学习价值函数等问题,特别是动作价值函数难以学习,原因是联合动作空间随智能体个数呈指数增长的问题,因此本文章学习如何有效的学习价值函数且最大化共同和奖励过程
1、价值分解的研究现状
价值函数如何分解才能更好的学习已经具有很长的研究历史,通过多智能体在交互过程中并非所有智能体互相之间都存在交互过程这一观点,提出了coordination graph,稀疏的协作图能够近似联合动作函数作为交互智能体的价值和,能够更高效的评估价值,例子如下:
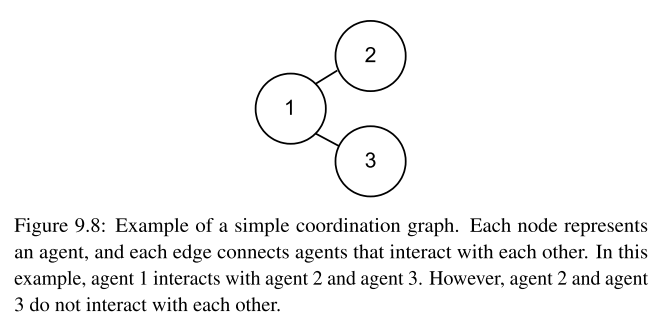
在共同和奖励过程,已经有很多成功的价值分解算法应用到价值函数的学习中,价值分解算法能够将价值函数分解为更简单的函数,在共同和奖励过程能够更高效的学习,中心动作价值函数能够表示为如下(共同奖励过程):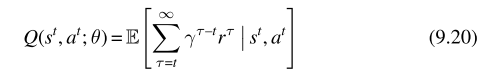
2、Individual-Global-Max Property
最简单的分解Q函数的方法便是每个智能体单独学习效用函数,只与其历史观测序列与动作有关,这些效用函数采用相同的结构如下所示:
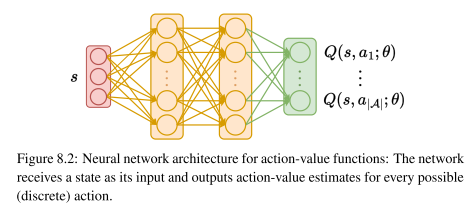
之所以称为效用函数是这些函数并不会去学习如何近似自身的期望回报,而是将所有智能体的效用函数联合优化近似中心动作价值函数并且满足individual-global-max(IGM)性质
为了定义IGM性质,引入中心化动作价值函数与效用函数的贪婪动作,如下所示: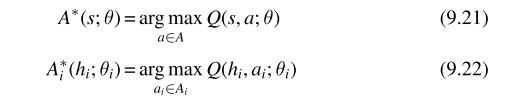
其中 Q ( s , a ; θ ) Q(s,a;\theta) Q(s,a;θ)表示中心动作价值函数、 Q ( h i , a i ; θ i ) Q(h_{i},a_{i};\theta_{i}) Q(hi,ai;θi)表示智能体i的效用函数
IGM性质满足以下关系:
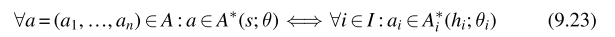
解释:如果联合动作相对于中心动作价值函数是贪婪的,那么相对于效用函数来说每个智能体i在联合动作中自身的动作也是贪婪的,也就是说如果智能体i相对于自身的效用函数选择贪婪动作,那么相对于分解中心动作价值函数,单个贪婪动作组成的联合动作也是贪婪的
在满足IGM的条件下,每个智能体能够根据自身的效用函数选择贪婪动作,那么所有的智能体能够一起选择贪婪的联合动作,效用函数除了能够简单的分解中心动作价值函数之外,还能够评估每个智能体在共同奖励过程中的贡献,这样来看,价值分解还能够在一定程度上减轻信用分配问题
3、Linear and Monotonic Value Decomposition
3.1线性值分解
满足IGM性质是假设共同奖励过程满足线性分解,每个智能体单独的奖励等于整体的奖励
r t = r ‾ 1 t + ⋯ + r ‾ n t r^{t}=\overline{r}_{1}^{t}+\cdots+\overline{r}_{n}^{t} rt=r1t+⋯+rnt
在改假设的基础之上,中心动作价值函数能够分解为如下:

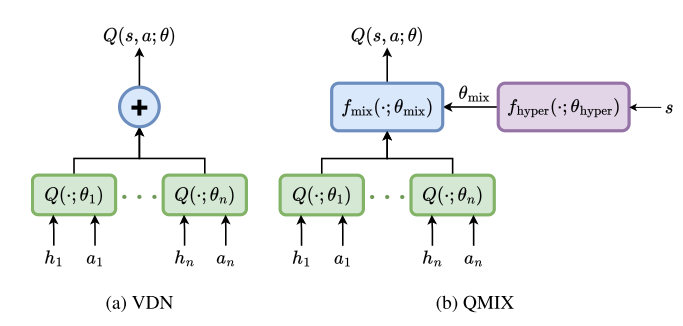
基于线性的分解方法提出VDN算法,通过维护包含所有智能体经验的回收池以及采用所有智能体联合优化得到近似中心化价值函数,其损失函数如下:
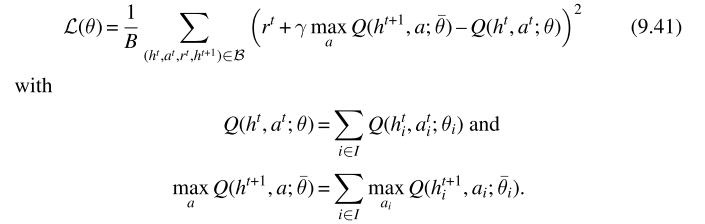
3.2 单调值分解
在一些情况下,每个智能体的贡献在非线性的情况下具有更好的表现,线性分解无法起到作用
在满足IGM的前提下,还需要满足中心化动作价值函数相对于每个智能体的效用函数的导数为正,如下图所示:
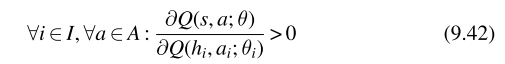
那就意味着每个智能体采取动作后效用函数增加,那么采取相对应联合动作后中心价值函数也会增加
QMIX网络采用DQN作为每个智能体的效用函数,同时定义了一个混合网络用于聚合所有智能体的效用网络近似中心化的动作价值函数
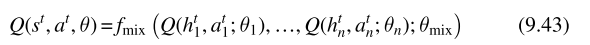
在实际应用中,mix网络对于输入的权重均为正,通常mixing函数的参数通过额外的超参数网络获得,该网络用所有的状态作为输入,输出mixing网络的参数,为了保证mixing网络参数为正,超参网络采用绝对值函数作为激活函数,联合优化损失函数如下:

中心动作价值函数能够用如下的等式简单表达
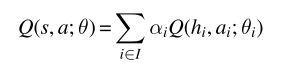
其中的权重系数均大于等于0,代表对应智能体的贡献,若系数为1,则代表线性分解
**一些值得注意的点:**首先所有的智能体的效用网络参数是共享的、智能体通过onehot编码进行区别、智能体效用网络能够建模成RNN网络、每个episode会存储所有的经验,在其结束后进行更新
相关文章:
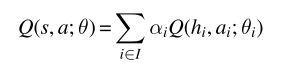
10MARL深度强化学习 Value Decomposition in Common-Reward Games
文章目录 前言1、价值分解的研究现状2、Individual-Global-Max Property3、Linear and Monotonic Value Decomposition3.1线性值分解3.2 单调值分解 前言 中心化价值函数能够缓解一些多智能体强化学习当中的问题,如非平稳性、局部可观测、信用分配与均衡选择等问题…...

2 Nacos适配达梦数据库实现方案
1、修改源代码方式 Nacos 原生是不支持达梦数据库的,所以就要想办法让它 “支持”,因为是开源软件,我们可以从源码入手,在流行的 1.x 、2.x 或最新版本代码的基本上进行修改。 主要涉及到以下内容的修改: com/alibaba/nacos/persistence/datasource/ExternalDataS...
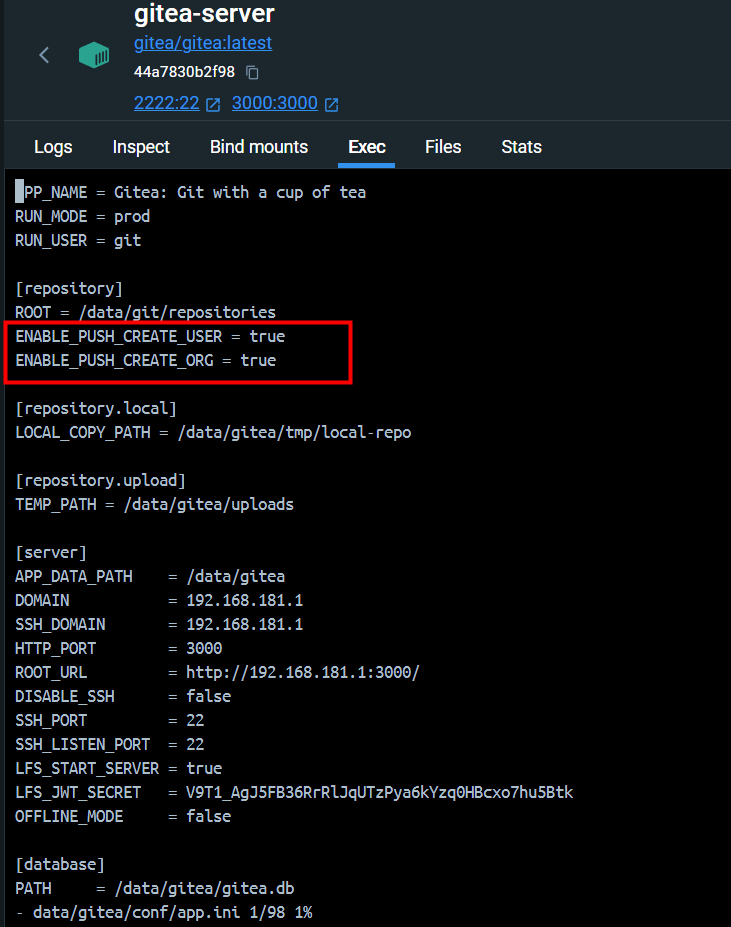
【Gitea】配置 Push To Create
引 在 Git 代码管理工具使用过程中,经常需要将一个文件夹作为仓库上传到一个未创建的代码仓库。如果 Git 服务端使用的是 Gitea,通常会推送失败。 PS D:\tmp\git-test> git remote add origin http://192.1.1.1:3000/root/git-test.git PS D:\tmp\g…...
)
关于postgresql数据库单独设置某个用户日志级别(日志审计)
前言: 很多时候我们想让数据库日志打印详细一点,但是又担心会对数据库本身产生一些不可控的影响,还会担心数据库产生的庞大的日志导致主机资源不太够用的影响。那么今天我们就通过讲解给单个用户设置 log_statement来解决以上这些问题。 注…...
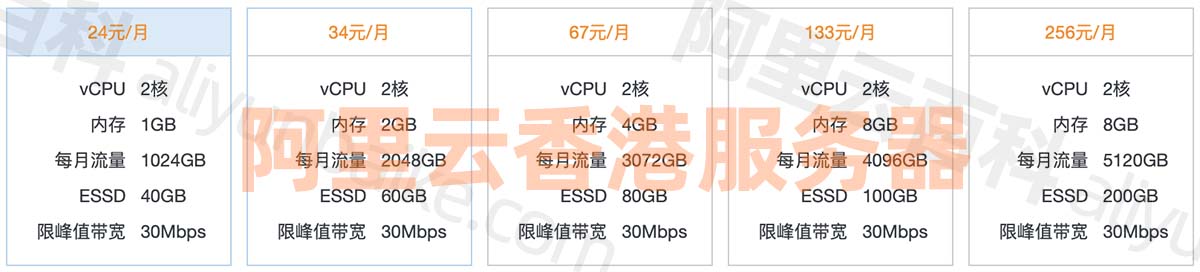
阿里云ECS香港服务器性能强大、cn2高速网络租用价格表
阿里云香港服务器中国香港数据中心网络线路类型BGP多线精品,中国电信CN2高速网络高质量、大规格BGP带宽,运营商精品公网直连中国内地,时延更低,优化海外回中国内地流量的公网线路,可以提高国际业务访问质量。阿里云服务…...
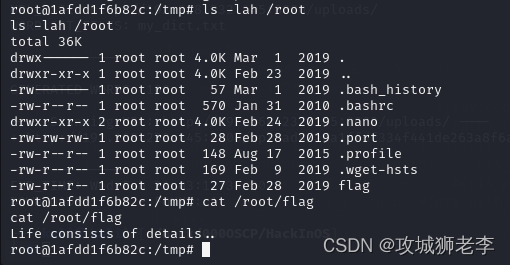
实战打靶集锦-025-HackInOS
文章目录 1. 主机发现2. 端口扫描3. 服务枚举4. 服务探查5. 提权5.1 枚举系统信息5.2 探索一下passwd5.3 枚举可执行文件5.4 查看capabilities位5.5 目录探索5.6 枚举定时任务5.7 Linpeas提权 靶机地址:https://download.vulnhub.com/hackinos/HackInOS.ova 1. 主机…...
.forEach()和list.forEach()的区别)
list.stream().forEach()和list.forEach()的区别
list.stream().forEach() 和 list.forEach() 在 Java 中都是用于遍历集合元素的方法,但它们在使用场景和功能上有所不同: list.forEach(): 是从 Java 8 开始引入到 java.util.List 接口的标准方法。直接对列表进行迭代,它采用内部…...
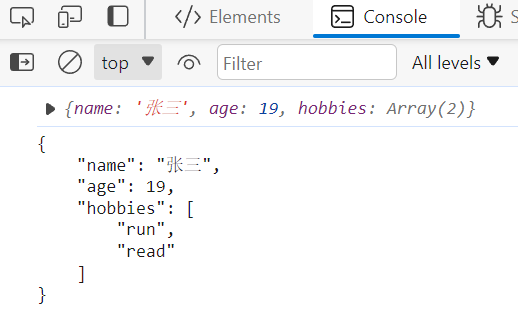
JS基础之JSON对象
JS基础之JSON对象 目录 JS基础之JSON对象对象转JSON字符串JSON转JS对象 对象转JSON字符串 JSON.stringify(value,replacer,space) value:要转换的JS对象 replacer:(可选)用于过滤和转换结果的函数或数组 space:(可选)指定缩进量 // 创建JS对象 let date {name:"张三…...
嵌入式学习之Linux入门篇——使用VMware创建Unbuntu虚拟机
目录 主机硬件要求 VMware 安装 安装Unbuntu 18.04.6 LTS 新建虚拟机 进入Unbuntu安装环节 主机硬件要求 内存最少16G 硬盘最好分出一个单独的盘,而且最少预留200G,可以使用移动固态操作系统win7/10/11 VMware 安装 版本:VMware Works…...

大模型中的token是什么?
定义 大模型的"token"是指在自然语言处理(NLP)任务中,模型所使用的输入数据的最小单元。这些token可以是单词、子词或字符等,具体取决于模型的设计和训练方式。 大模型的token可以是单词级别的,也可以是子…...
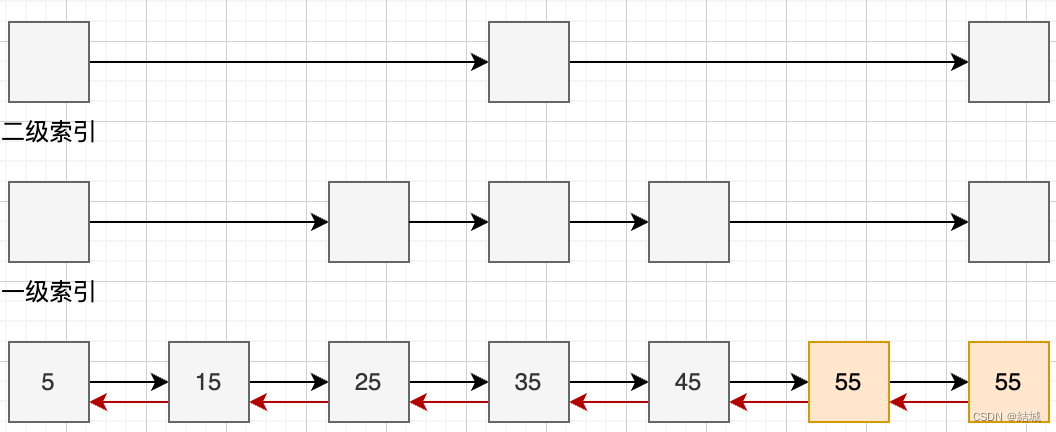
跳表是一种什么样的数据结构
跳表是有序集合的底层数据结构,它其实是链表的一种进化体。正常链表是一个接着一个用指针连起来的,但这样查找效率低只有O(n),为了解决这个问题,提出了跳表,实际上就是增加了高级索引。朴素的跳表指针是单向的并且元素…...

【刷题记录】最大公因数,最小公倍数(辗转相除法、欧几里得算法)
本系列博客为个人刷题思路分享,有需要借鉴即可。 1.题目链接: 无 2.详解思路: 题目描述:输入两个正整数,输出其最大公因数和最小公倍数 一般方法:最大公因数:穷加法;最小公倍数&…...
ETL快速拉取物流信息
我国作为世界第一的物流大国,但是在目前的物流信息系统还存在着几大的痛点。主要包括以下几个方面: 数据孤岛:有些物流企业各个部门之间的数据标准不一致,难以实现数据共享和协同,容易导致信息孤岛。 操作繁琐&#x…...
)
17.1 SpringMVC框架_SpringMVC入门与数据绑定(❤❤)
17.1 SpringMVC框架_SpringMVC入门与数据绑定 1. SpringMVC入门1.1 MVC介绍1.2 环境配置1. 依赖引入2. web配置文件:DispatchServlet配置3. applicationContext.xml配置4. 开发Controller控制器(❤❤)1.3 MVC处理流程图2. Spring MVC数据绑定2.1 URL Mapping2.2 URL Mapping三个…...
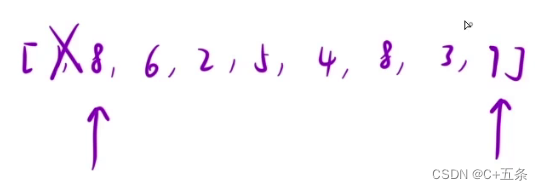
Leetcode 11.盛水最多的容器
题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明:你不能倾斜容器。…...

《Go 简易速速上手小册》第7章:包管理与模块(2024 最新版)
文章目录 7.1 使用 Go Modules 管理依赖 - 掌舵向未来7.1.1 基础知识讲解7.1.2 重点案例:Web 服务功能描述实现步骤扩展功能7.1.3 拓展案例 1:使用数据库功能描述实现步骤扩展功能7.1.4 拓展案例 2:集成 Redis 缓存功能描述实现步骤...

【论文精读】IBOT
摘要 掩码语言建模(MLM)是一种流行的语言模型预训练范式,在nlp领域取得了巨大的成功。然而,它对视觉Transformer (ViT)的潜力尚未得到充分开发。为在视觉领域延续MLM的成功,故而探索掩码图像建模(MIM),以训练更好的视觉transforme…...

Yolo V5在实时视频流中的建筑物与彩钢房检测:性能评估与改进方法
Yolo V5在实时视频流中的建筑物与彩钢房检测:性能评估与改进方法 文章目录 Yolo V5在实时视频流中的建筑物与彩钢房检测:性能评估与改进方法概述Yolo V5模型概述建筑物与彩钢房检测的挑战实时视频流处理流程模型性能评估改进方法实验与分析结论与展望 概…...
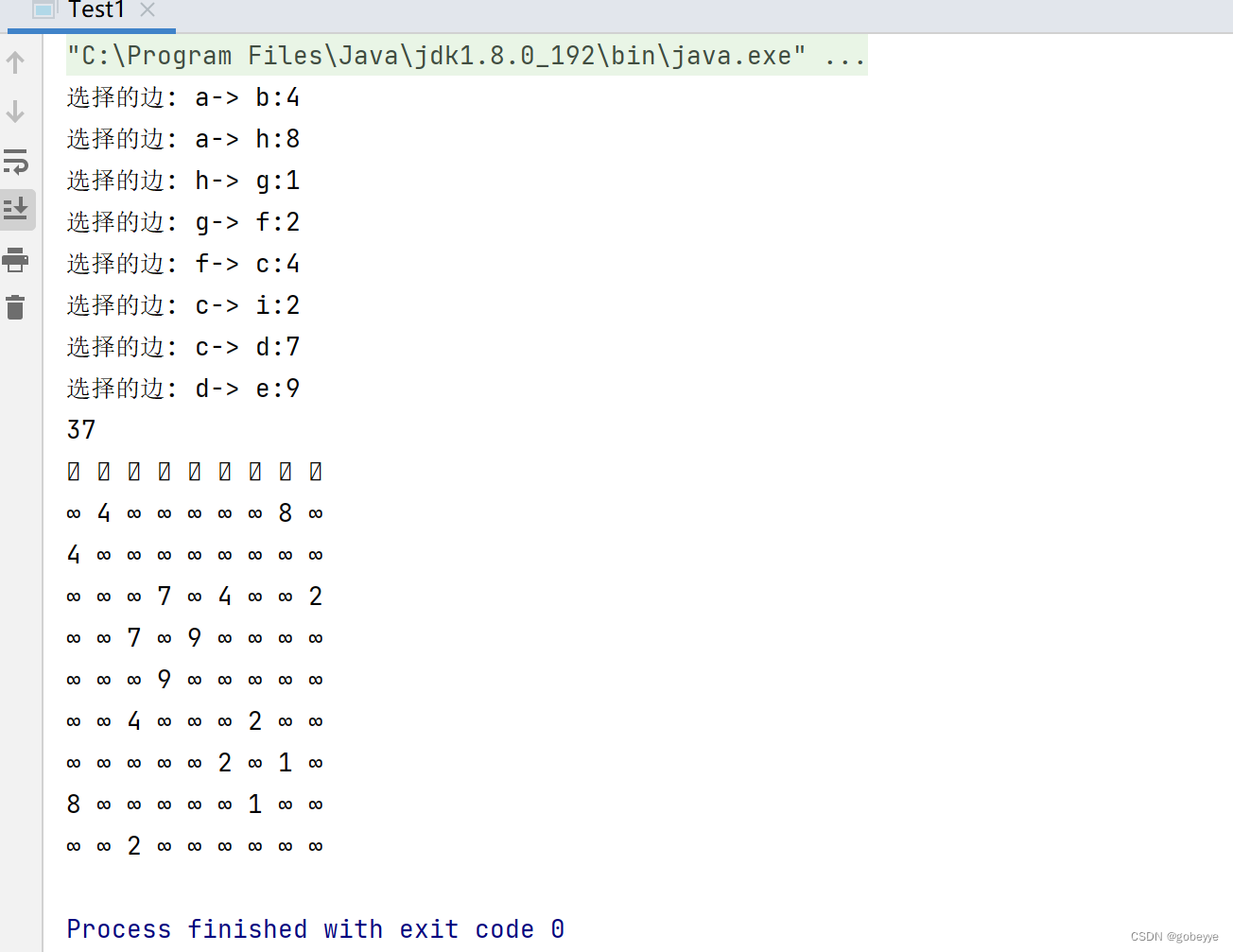
图——最小生成树实现(Kruskal算法,prime算法)
目录 预备知识: 最小生成树概念: Kruskal算法: 代码实现如下: 测试: Prime算法 : 代码实现如下: 测试: 结语: 预备知识: 连通图:在无向图…...

Unity3D xLua开发环境搭建详解
前言 xLua是一种基于Lua语言的开发框架,可以帮助开发者在Unity3D中使用Lua脚本来开发游戏。 对惹,这里有一个游戏开发交流小组,希望大家可以点击进来一起交流一下开发经验呀! 在本文中,我们将详细介绍如何搭建Unity…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...
