Leetcode 11.盛水最多的容器
题目
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
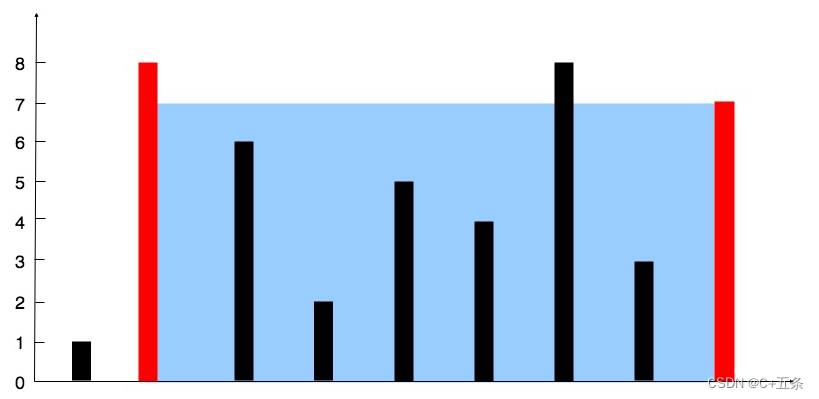
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1] 输出:1
思路
题目给定一个数组让求最大容量,有以下两种方法
一、暴力枚举
从下标0开始把所有情况全部算出来求最大,及其原始暴力的方法,作为一个学习算法和编程的人,首先排除此方法。
二、双指针
此类型题目可以理解为日常生活中所说的木桶效应,一个木桶能装多少水是由最短的那块板子来决定的,同样在计算容积时,高是由最短的那个数来决定的,而想要从数组中找出最优解,枚举是不可缺少的,但要尽可能的控制枚举的次数,从而降低代码的时间复杂度。
用h表示高,w表示宽
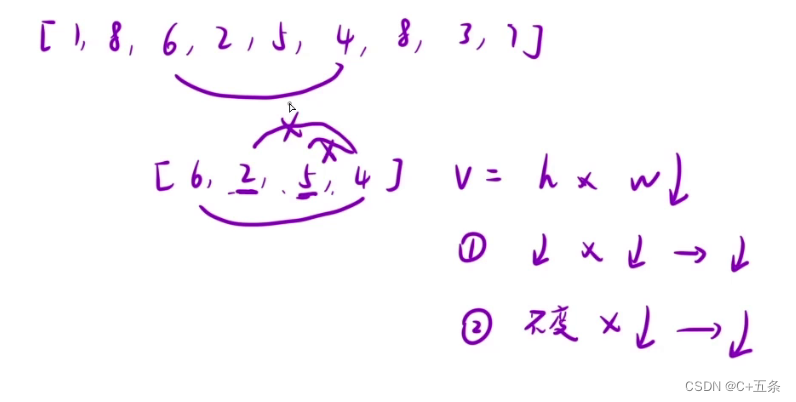
从中间随机截取一段来举例,[6,2,5,4]首先可以算出体积为3*4=12,现在假设拿4依次根其他几个数作枚举,w无疑是在减小的,那么现在会出现两种情况:
但只要仔细观察就会发现无论哪种情况,总容量都是在减少的。
1.h比4小,和刚开始比h减小了w也减小了,容量无疑也减小了。
2.h比4大,那高度还得是4,所以和刚开始比h不变,w减小,容积量在减小。
所以当在一个区间内选最左和最右两个数算出容积之后,两个数中小的那个数已经完全没有必要再去向内进行枚举了,因为无论怎么枚举,容量都是变小的。此时4可以直接不考虑了。
我们可以知道,容量是受宽和高的影响的,而我们需要找出的就是一个宽和高都相对较高的值,结合上面的分析,所以为了加快效率,两个指针一个在前一个在后同时由外向内进行遍历可以大大节约时间,那边小直接向内移动那边,然后计算容量,这样就可以用O(n)的时间复杂度来找出最大容量了。
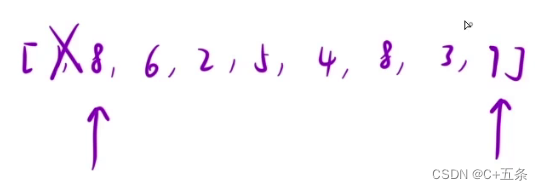
扩大到整个数组,最左最右计算完直接干掉1向右移,继续找,如果比之前算出来的都大就更新max。
题解
class Solution {
public:int maxArea(vector<int>& height) {int left=0,right=height.size()-1;int max=0,h=0,w=0;while(left<right){w=right-left;if(height[left]<height[right]) h=height[left++];else h=height[right--];if(w*h>max) max=w*h;}return max;}
};相关文章:
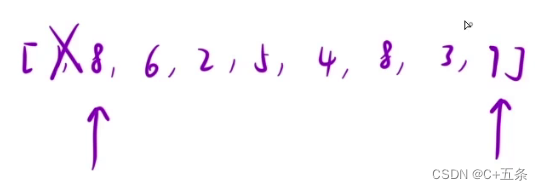
Leetcode 11.盛水最多的容器
题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明:你不能倾斜容器。…...

《Go 简易速速上手小册》第7章:包管理与模块(2024 最新版)
文章目录 7.1 使用 Go Modules 管理依赖 - 掌舵向未来7.1.1 基础知识讲解7.1.2 重点案例:Web 服务功能描述实现步骤扩展功能7.1.3 拓展案例 1:使用数据库功能描述实现步骤扩展功能7.1.4 拓展案例 2:集成 Redis 缓存功能描述实现步骤...

【论文精读】IBOT
摘要 掩码语言建模(MLM)是一种流行的语言模型预训练范式,在nlp领域取得了巨大的成功。然而,它对视觉Transformer (ViT)的潜力尚未得到充分开发。为在视觉领域延续MLM的成功,故而探索掩码图像建模(MIM),以训练更好的视觉transforme…...

Yolo V5在实时视频流中的建筑物与彩钢房检测:性能评估与改进方法
Yolo V5在实时视频流中的建筑物与彩钢房检测:性能评估与改进方法 文章目录 Yolo V5在实时视频流中的建筑物与彩钢房检测:性能评估与改进方法概述Yolo V5模型概述建筑物与彩钢房检测的挑战实时视频流处理流程模型性能评估改进方法实验与分析结论与展望 概…...
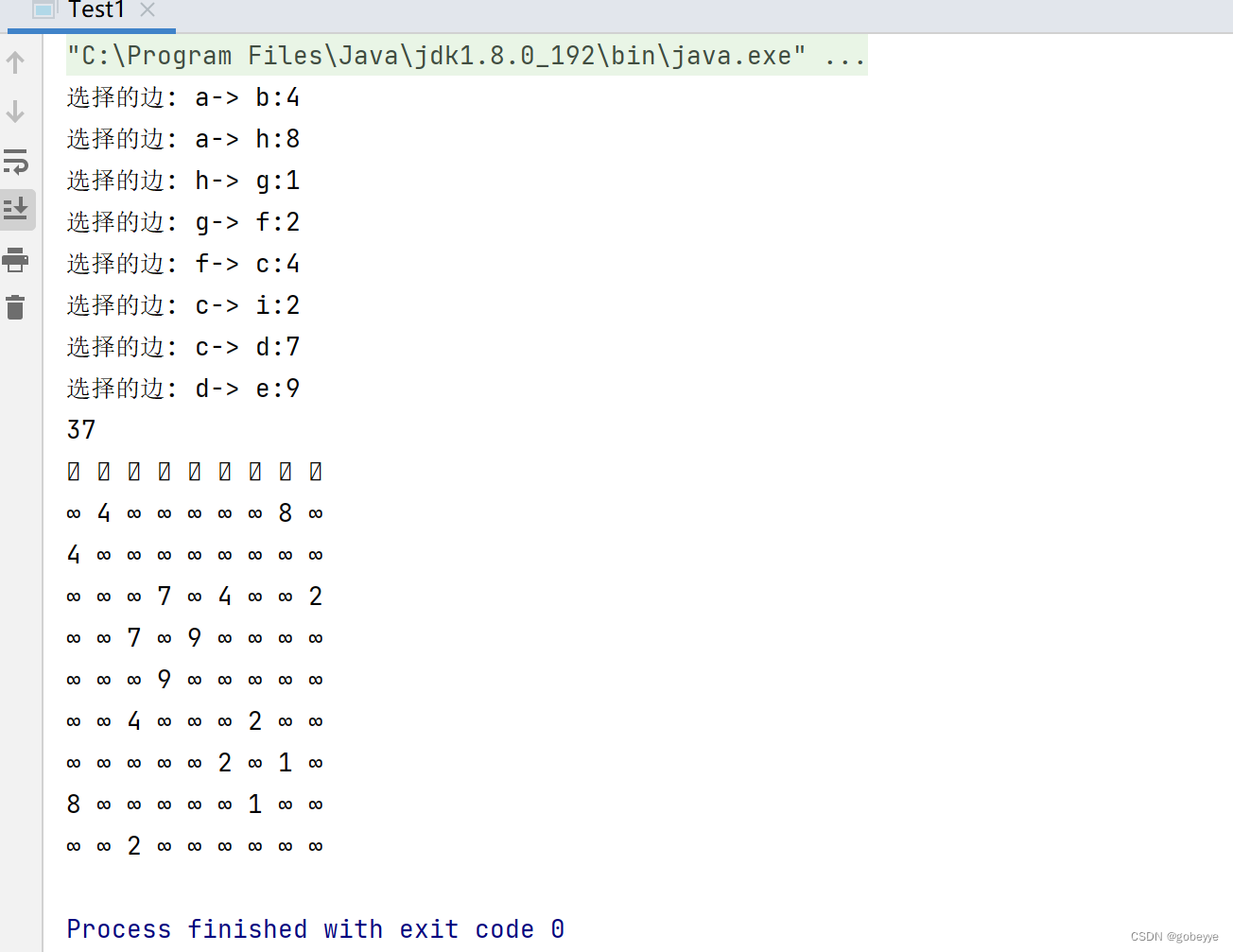
图——最小生成树实现(Kruskal算法,prime算法)
目录 预备知识: 最小生成树概念: Kruskal算法: 代码实现如下: 测试: Prime算法 : 代码实现如下: 测试: 结语: 预备知识: 连通图:在无向图…...

Unity3D xLua开发环境搭建详解
前言 xLua是一种基于Lua语言的开发框架,可以帮助开发者在Unity3D中使用Lua脚本来开发游戏。 对惹,这里有一个游戏开发交流小组,希望大家可以点击进来一起交流一下开发经验呀! 在本文中,我们将详细介绍如何搭建Unity…...
.init(root)的作用)
Python笔记-super().init(root)的作用
假设我们有一个名为Animal的父类,它有一个属性color,在其构造函数__init__中被初始化: class Animal:def __init__(self, color):self.color color现在,我们想创建一个Animal的子类,名为Dog。Dog类有自己的属性name&…...
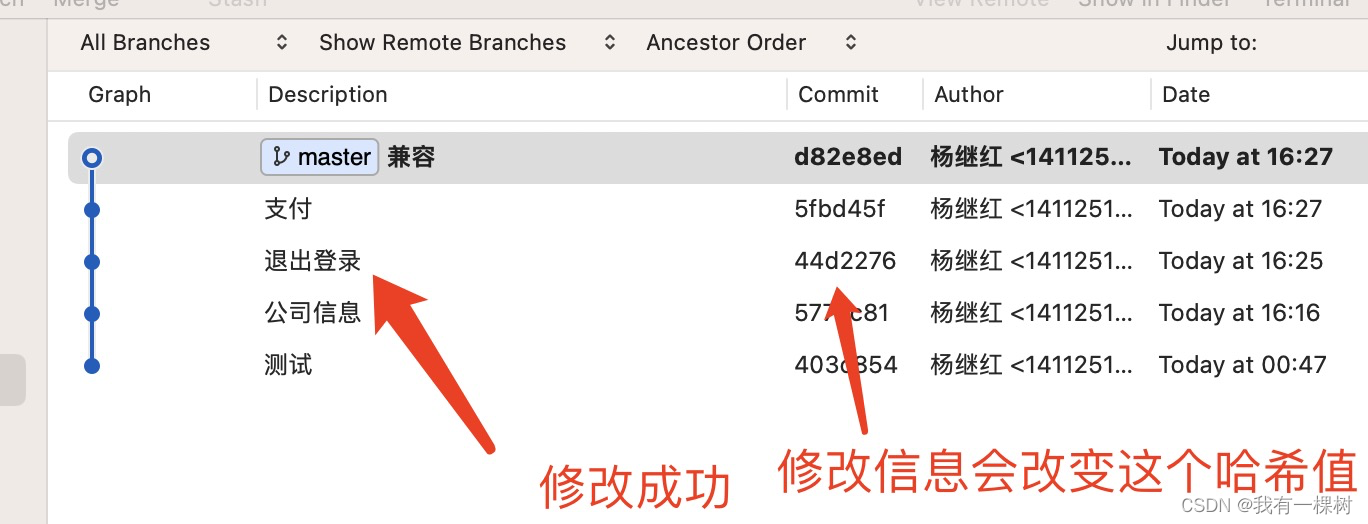
【git 使用】使用 git rebase -i 修改任意的提交信息/合并多个提交
修改最近一次的提交信息的方法有很多,可以参考这篇文章,但是对于之前的提交信息进行修改只能使用 rebase。 修改提交信息 假设我们想修改下面这个提交信息,想把【登录】改成【退出登录】步骤如下 运行 git rebase -i head~3 打开了一个文本…...

【Vue3】toRefs和toRef在reactive中的一些应用
💗💗💗欢迎来到我的博客,你将找到有关如何使用技术解决问题的文章,也会找到某个技术的学习路线。无论你是何种职业,我都希望我的博客对你有所帮助。最后不要忘记订阅我的博客以获取最新文章,也欢…...
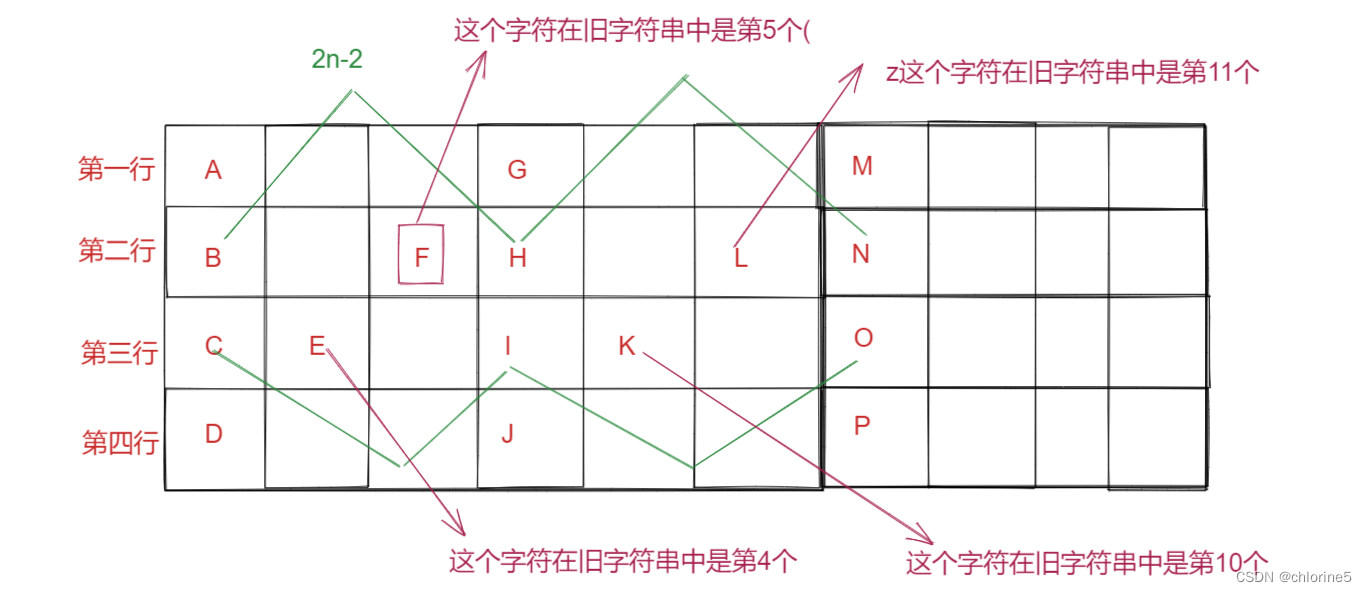
力扣精选算法100道——Z字形变换(模拟专题)
目录 🎈了解题意 🎈算法原理 🚩先处理第一行和最后一行 🚩再处理中间行 🎈实现代码 🎈了解题意 大家看到这个题目的时候肯定是很迷茫的,包括我自己也是搞不清楚题目什么意思,我…...
Elastic Stack--01--简介、安装
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1. Elastic Stack 简介为什么要学习ESDB-Engines搜索引擎类数据库排名常年霸榜
.NET项目web自动化测试实战——Selenium 2.0
🔥 交流讨论:欢迎加入我们一起学习! 🔥 资源分享:耗时200小时精选的「软件测试」资料包 🔥 教程推荐:火遍全网的《软件测试》教程 📢欢迎点赞 👍 收藏 ⭐留言 …...

【Day53】代码随想录之动态规划_买卖股票ⅠⅡ
文章目录 动态规划理论基础动规五部曲:出现结果不正确: 1. 买卖股票的最佳时机2. 买卖股票的最佳时机Ⅱ 动态规划理论基础 动规五部曲: 确定dp数组 下标及dp[i] 的含义。递推公式:比如斐波那契数列 dp[i] dp[i-1] dp[i-2]。初…...
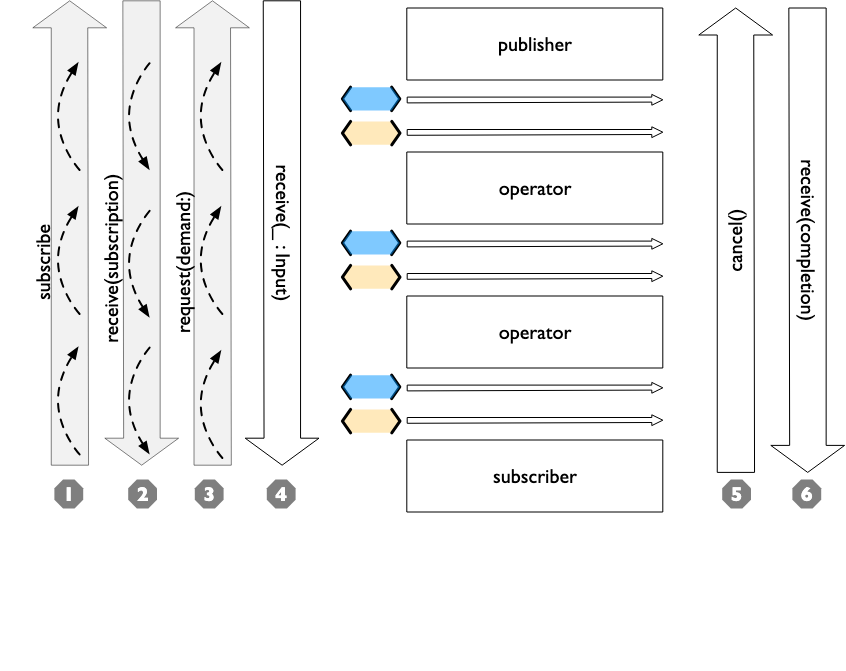
Swift Combine 使用调试器调试管道 从入门到精通二十六
Combine 系列 Swift Combine 从入门到精通一Swift Combine 发布者订阅者操作者 从入门到精通二Swift Combine 管道 从入门到精通三Swift Combine 发布者publisher的生命周期 从入门到精通四Swift Combine 操作符operations和Subjects发布者的生命周期 从入门到精通五Swift Com…...

go内置库函数实现client与server数据的发送接收
功能:客户端持续写入数据,直到输入exit退出,服务端读取数据并打印 注意:server和client目录在同一层级 服务端 server/main package mainimport ("fmt""net" )func main() {listen, err : net.Listen(&quo…...
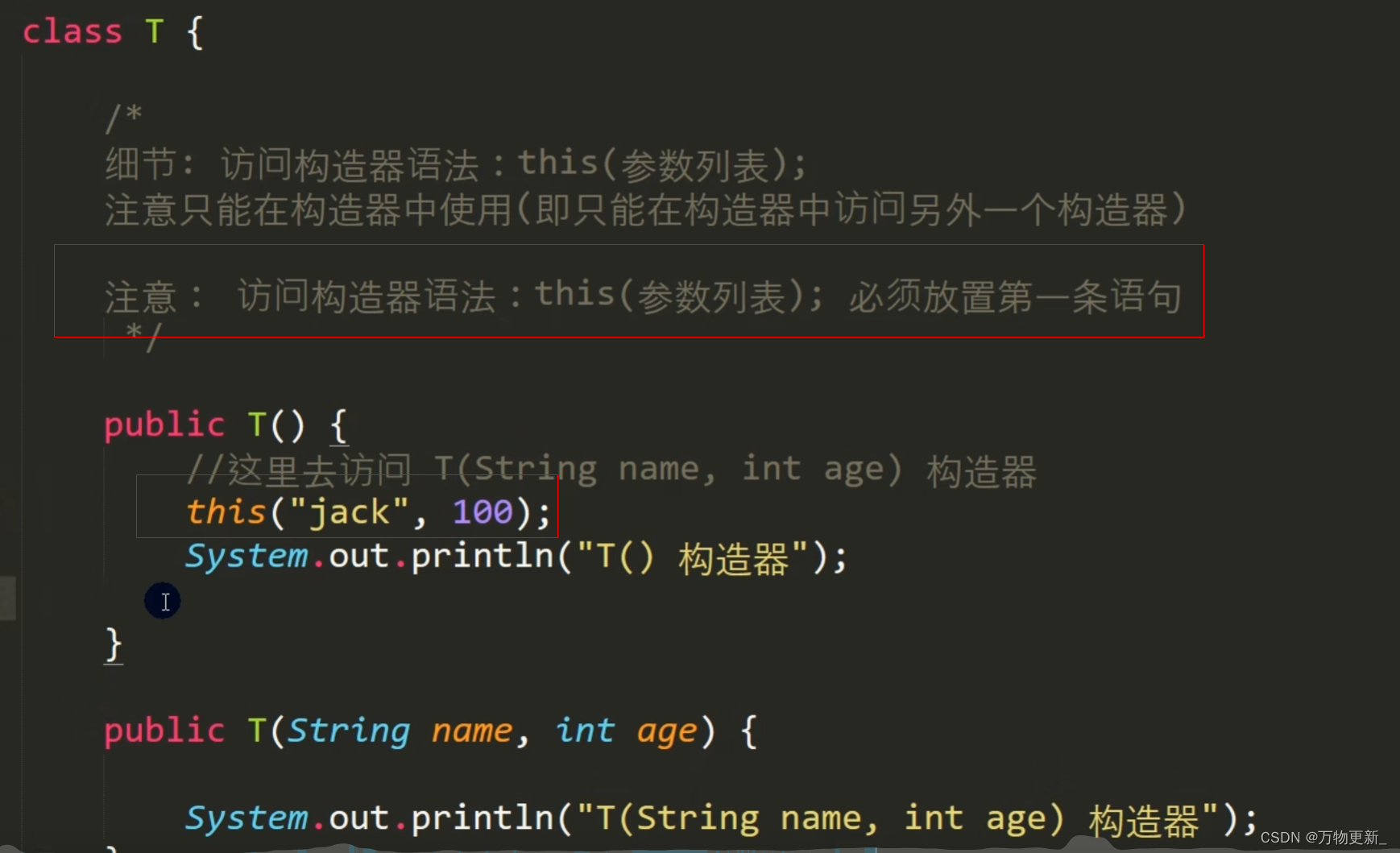
[java基础揉碎]this
引出this: 什么是this: java虚拟机会给每个对象分配 this,代表当前对象。 这里的this就是new出来的这个对象 this的本质: this是个引用在堆中指向它自己: this的细节: 访问成员方法: 访问构造器:...

vulnhub靶场之Deathnote
一.环境搭建 1.靶场描述 Level - easy Description : dont waste too much time thinking outside the box . It is a Straight forward box . This works better with VirtualBox rather than VMware 2.靶场下载 https://www.vulnhub.com/entry/deathnote-1,739/ 3.启动环…...

Docker安装Postgresql12
1、搜索仓库中postgres docker search postgres 2、拉取镜像 docker pull postgres docker pull postgres:12 #拉取12版本的PG库 3、创建数据库文件夹 cd /temp/ && mkdir -m 755 postgres-data 注:-m表示权限,类chmod命令 4、执行命令启动…...

服务器防火墙的应用技术有哪些类型?
随着互联网的发展,网络安全问题更加严峻。服务器防火墙技术作为一种基础的网络安全技术,对于保障我们的网络安全至关重要。本文将介绍服务器防火墙的概念和作用,以及主要的服务器防火墙技术,包括数据包过滤、状态检测、代理服务、…...

IP地理位置查询定位:技术原理与实际应用
在互联网时代,IP地址是连接世界的桥梁,而了解IP地址的地理位置对于网络管理、个性化服务以及安全监控都至关重要。IP数据云将深入探讨IP地理位置查询定位的技术原理、实际应用场景以及相关的隐私保护问题,旨在为读者提供全面了解和应用该技术…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
