图——最小生成树实现(Kruskal算法,prime算法)
目录
预备知识:
最小生成树概念:
Kruskal算法:
代码实现如下:
测试:
Prime算法 :
代码实现如下:
测试:
结语:
预备知识:
连通图:在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。如果图中任意一 对顶点 都是连通的,则称此图为连通图。
生成树:一个连通图的生成树是指一个连通子图,它含有图中全部n个顶点,但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边,如果生成树中再添加一条边,则必定成环。
并查集:
由于本文章重点不在讲述并查集,故下面我简单描述并查集的作用,各种方法,源码如下。
并查集的作用:可以将一个数组中的元素分为多个小组的数据结构。
方法:
findRoot(x):查找x的根。
union(int x1, int x2):合并x1和x2。
isSameSet(int x1, int x2):判断两个数字 是不是在同一个集合当中。
import java.util.Arrays;public class UnionFindSet {private int[] elem;//底层是数组public UnionFindSet(int n){this.elem = new int[n];Arrays.fill(elem,-1);//整体初始化为-1:代表根}/*** 查找x的根* @param x* @return*/public int findRoot(int x){if(x < 0){throw new IndexOutOfBoundsException("数据不合法");}while(elem[x] >= 0){x = elem[x];}return x;}/*** 合并x1和x2* @param x1* @param x2*/public void union(int x1,int x2){int index1 = findRoot(x1);int index2 = findRoot(x2);if(index1 == index2){//说明x1和x2的根是相同的,不需要进行合并return;}elem[index1] = elem[index1] + elem[index2];elem[index2] = index1;//将x2合并到x1}/*** 判断两个数字是不是在同一个集合当中* @param x1* @param x2* @return*/public boolean isSameSet(int x1,int x2){int index1 = findRoot(x1);int index2 = findRoot(x2);if(index1 == index2){return true;}else{return false;}}
}
最小生成树概念:
连通图中的每一棵生成树,都是原图的一个极大无环子图,即:从其中删去任何一条边,生成树 就不在连通;反之,在其中引入任何一条新边,都会形成一条回路。
若连通图由n个顶点组成,则其生成树必含n个顶点和n-1条边。因此构造最小生成树的准则有三 条:
(1) 只能使用图中的边来构造最小生成树。
(2) 只能使用恰好n-1条边来连接图中的n个顶点。
(3) 选用的n-1条边不能构成回路。
构造最小生成树的方法:Kruskal算法和Prim算法。这两个算法都采用了逐步求解的贪心策略。
贪心算法:是指在问题求解时,总是做出当前看起来最好的选择。也就是说贪心算法做出的不是整体最优的选择,而是某种意义上的局部最优解。贪心算法不是对所有的问题都能得到整体最优解。
Kruskal算法:
Kruskal算法采用全局贪心的策略,其步骤如下:
任给一个有n个顶点的连通网络N={V,E}。
(1)首先构造一个由这n个顶点组成、不含任何边的图G={V,NULL},其中每个顶点自成一个连通分量。
(2)其次不断从E中取出权值最小的一条边(若有多条任取其一),若该边的两个顶点来自不同的连通分量(若相同则不加因为会生成环),则将此边加入到G中。
(3)如此重复,直到所有顶点在同一个连通分量上为止。
核心:每次迭代时,选出一条具有最小权值,且两端点不在同一连通分量上的边,加入生成树。
具体过程如下图所示:按照abc..的循序,箭头为当前要操作的位置(不一定能添加,黑色为可添加)。

代码实现如下:
先构造关于Edge的小根堆,由于是自定义类,故要自己实现一个比较器Comparator。
1. 定义优先级队列存储边构建小根堆 跟进权重进行比较。
2. 把矩阵当中的边全部入队列。
3. 定义并查集判断将来两条边是不是在一个集合(避免构成环)。
4. 由于篇幅有限matrix之类的前文实现过这里不在实现有需要的友友可以前往图的概念
static class Edge{public int srcIndex;public int destIndex;public int weight;public Edge(int srcIndex,int destIndex,int weight){this.srcIndex = srcIndex;this.destIndex = destIndex;this.weight = weight;}}public int kruskal(GraphByMatrix minTree){//1. 定义优先级队列 存储边 构建小根堆 跟进权重进行比较PriorityQueue<Edge> minHeap = new PriorityQueue<>(new Comparator<Edge>(){@Overridepublic int compare(Edge o1,Edge o2){return o1.weight - o2.weight;}});int n = matrix.length;//2. 把矩阵当中的边全部入队列for(int i = 0;i < n;i++){for(int j = 0;j < n;j++){//因为是无向图,所以只入一半就可以 i < j 即可if(i < j && matrix[i][j] != Integer.MAX_VALUE){Edge edge = new Edge(i,j,matrix[i][j]);minHeap.offer(edge);}}}//3、最后整个的权重int totalWeight = 0;int size= 0;//4.定义并查集 判断将来两条边 是不是在一个集合UnionFindSet ufs = new UnionFindSet(n);//5. 出优先级队列的n-1条边while(size < n-1 &&!minHeap.isEmpty()){Edge min = minHeap.poll();int srcIndex = min.srcIndex;int destIndex = min.destIndex;//判断是不在在同一个集合当中,在一个集合 就不能添加if(!ufs.isSameSet(srcIndex,destIndex)){//打印选出的边System.out.println("选择的边: "+ arrayV[srcIndex] + "-> "+ arrayV[destIndex] + ":"+matrix[srcIndex][destIndex]);?minTree.addEdgeUseIndex(srcIndex,destIndex,min.weight);totalWeight += min.weight;//添加完成之后,说明 可以 合并到同一个集合ufs.union(srcIndex,destIndex);size++;}}//如果是 选出n-1条边,否则就说明不是连通图if(size == n-1){return totalWeight;}//不是连通图, 可能选不出n-1条边 假设一个图中,有其他的顶点独立着return -1;}private void addEdgeUseIndex(int srcIndex,int destIndex,int weight) {matrix[srcIndex][destIndex] = weight;//如果是无向图 那么相反的位置 也同样需要置为空if(!isDirect) {matrix[destIndex][srcIndex] = weight;}}测试:
测试代码对应的图:
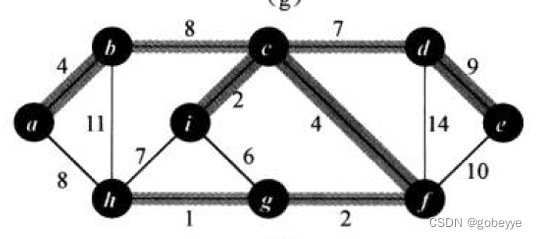
测试代码 :
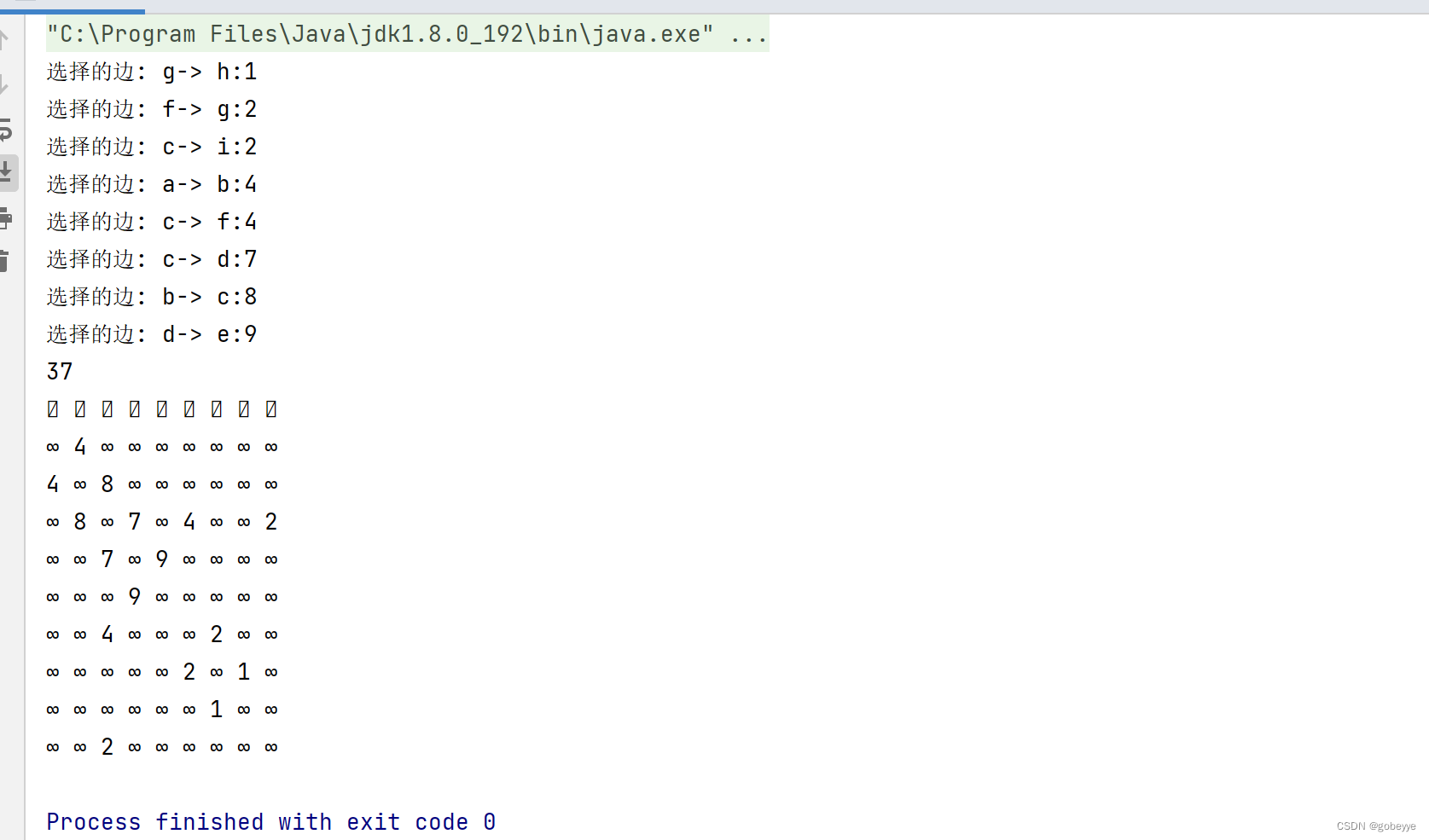
public static void main(String[] args) {testGraphMinTreeKruskal();}public static void testGraphMinTreeKruskal() {String str = "abcdefghi";char[] array =str.toCharArray();GraphByMatrix g = new GraphByMatrix(str.length(),false);g.initArrayV(array);g.addEdge('a', 'b', 4);g.addEdge('a', 'h', 8);//g.addEdge('a', 'h', 9);g.addEdge('b', 'c', 8);g.addEdge('b', 'h', 11);g.addEdge('c', 'i', 2);g.addEdge('c', 'f', 4);g.addEdge('c', 'd', 7);g.addEdge('d', 'f', 14);g.addEdge('d', 'e', 9);g.addEdge('e', 'f', 10);g.addEdge('f', 'g', 2);g.addEdge('g', 'h', 1);g.addEdge('g', 'i', 6);g.addEdge('h', 'i', 7);GraphByMatrix kminTree = new GraphByMatrix(str.length(),false);System.out.println(g.kruskal(kminTree));kminTree.printGraph();}效果:
显然正确💯
Prime算法 :
Primel算法采用局部贪心的策略,其步骤如下:
按照字母顺序abc....看。

代码实现如下:
由于是局部贪心用两个Set,那么天然就不会有环,故prime可以不用并查集。
1. 先获取当前顶点的下标。
2. 定义一个X集合,把当前的起点下标存进去。
3. 定义一个Y集合,存储目标顶点的元素。
4. 除了刚刚的起点,其他的顶点需要放到Y。
5. 从X集合中的点到Y集合的点中,连接的边中找出最小值放到优先级队列。
6. 把当前顶点连接出去的所有的边放入队列。
7.把这次的目标点,添加到X集合,变成了起点记得把之前的目标点,从Y集合删除掉。
8.遍历刚刚添加的新起点destIndex,连接出去的所有边,再次添加到优先级队列。
public int prim(GraphByMatrix minTree,char chV){//1. 先获取当前顶点的下标int srcIndex = getIndexOfV(chV);int n = arrayV.length;//2. 定义一个X集合,把当前的起点下标存进去Set<Integer> setX = new HashSet<>();//3. 定义一个Y集合,存储目标顶点的元素Set<Integer> setY = new HashSet<>();setX.add(srcIndex);//4. 除了刚刚的起点,其他的顶点需要放到Y集合for(int i = 0;i < n;i++){if(i != srcIndex){setY.add(i);}}//5. 从X集合中的点到Y集合的点中,连接的边中找出最小值放到优先级队列PriorityQueue<Edge> minHeap = new PriorityQueue<>(new Comparator<Edge>(){@Overridepublic int compare(Edge o1,Edge o2){return o1.weight - o2.weight;}});//6. 把当前顶点连接出去的所有的边放入队列for(int i = 0;i < n;i++){if(matrix[srcIndex][i] != Integer.MAX_VALUE){minHeap.offer(new Edge(srcIndex,i,matrix[srcIndex][i]));}}int size = 0;int totalWeight = 0;while(size < n - 1 && !minHeap.isEmpty()){//7. 取出队列中的第一条边Edge min = minHeap.poll();int srcI = min.srcIndex;int destI = min.destIndex;//起始点本身就在X集合,所以这里只需要判断目标点即可if(setX.contains(destI)){//包含}else{//8. 直接将该边 放入最小生成树minTree.addEdgeUseIndex(srcI,destI,min.weight);//9. 每选一条边 就打印一条语句System.out.println("选择的边: "+ arrayV[srcI] + "-> "+ arrayV[destI] + ":"+matrix[srcI][destI]);size++;totalWeight += min.weight;//10.把这次的目标点,添加到X集合,变成了起点setX.add(destI);//11.记得把之前的目标点,从Y集合删除掉setY.remove(destI);//12. 遍历刚刚添加的新起点destIndex,连接出去的所有边,再次添加到优先级队列for(int i = 0;i < n;i++){// 13. !setX.contains(i) 判断目标点不能再X这个集合 例如: a->b 就包含了b->aif(matrix[destI][i] != Integer.MAX_VALUE && !setX.contains(i)){minHeap.offer(new Edge(destI,i,matrix[destI][i]));}}}}if(size == n-1){return totalWeight;}else{return -1;}}测试:
测试对应的图:
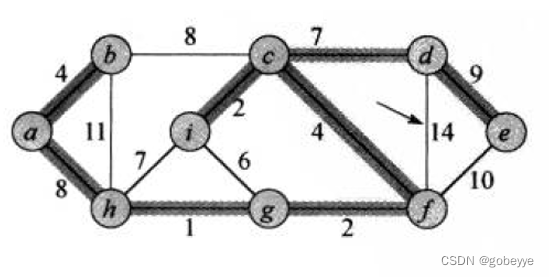
测试代码 :
public static void main(String[] args) {testGraphMinTreePrime();}public static void testGraphMinTreePrime() {String str = "abcdefghi";char[] array = str.toCharArray();GraphByMatrix g = new GraphByMatrix(str.length(), false);g.initArrayV(array);g.addEdge('a', 'b', 4);g.addEdge('a', 'h', 8);//g.addEdge('a', 'h', 9);g.addEdge('b', 'c', 8);g.addEdge('b', 'h', 11);g.addEdge('c', 'i', 2);g.addEdge('c', 'f', 4);g.addEdge('c', 'd', 7);g.addEdge('d', 'f', 14);g.addEdge('d', 'e', 9);g.addEdge('e', 'f', 10);g.addEdge('f', 'g', 2);g.addEdge('g', 'h', 1);g.addEdge('g', 'i', 6);g.addEdge('h', 'i', 7);GraphByMatrix primTree = new GraphByMatrix(str.length(), false);System.out.println(g.prim(primTree, 'a'));primTree.printGraph();}效果:
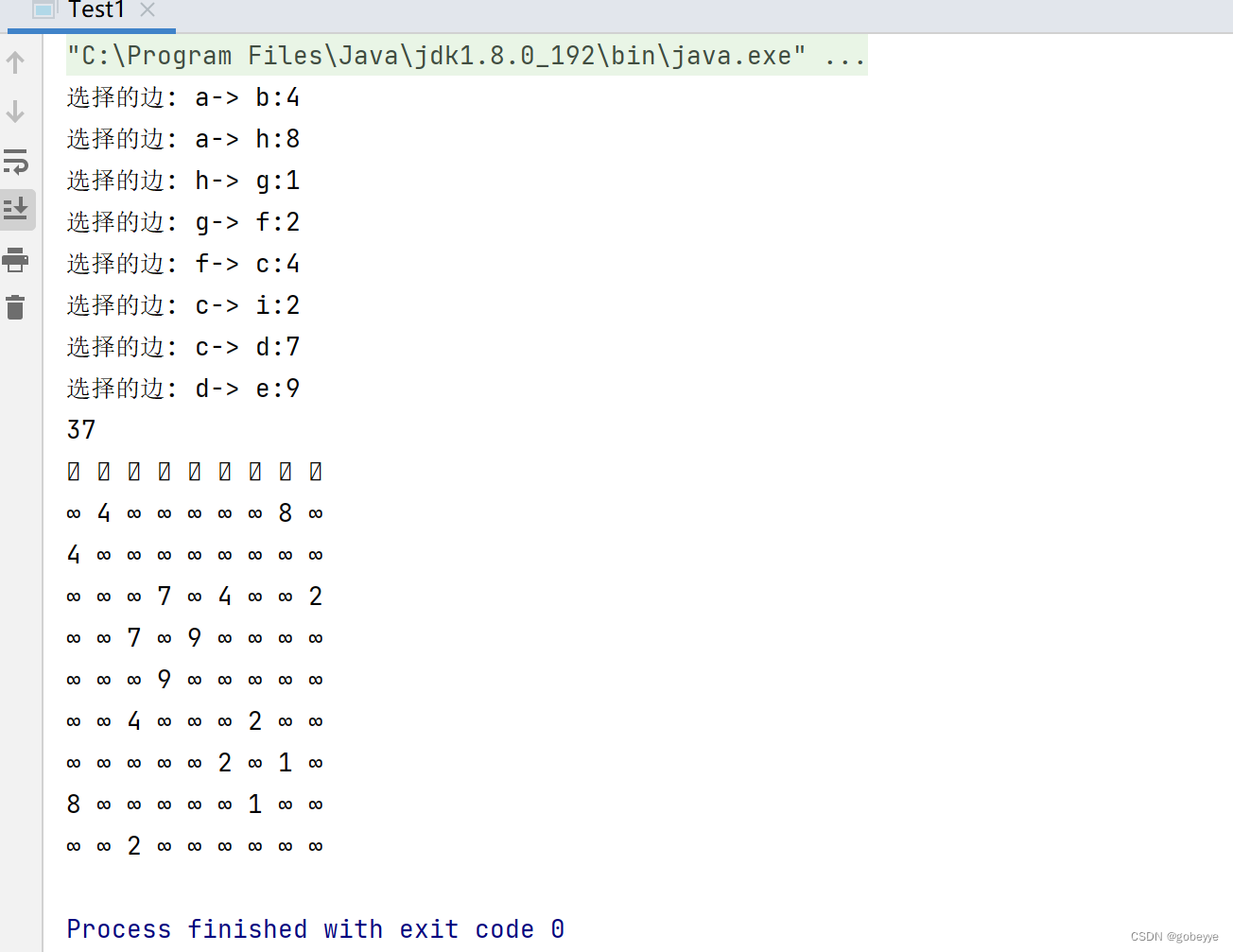
结语:
其实写博客不仅仅是为了教大家,同时这也有利于我巩固自己的知识点,和一个学习的总结,由于作者水平有限,对文章有任何问题的还请指出,接受大家的批评,让我改进,如果大家有所收获的话还请不要吝啬你们的点赞收藏和关注,这可以激励我写出更加优秀的文章。
相关文章:

图——最小生成树实现(Kruskal算法,prime算法)
目录 预备知识: 最小生成树概念: Kruskal算法: 代码实现如下: 测试: Prime算法 : 代码实现如下: 测试: 结语: 预备知识: 连通图:在无向图…...

Unity3D xLua开发环境搭建详解
前言 xLua是一种基于Lua语言的开发框架,可以帮助开发者在Unity3D中使用Lua脚本来开发游戏。 对惹,这里有一个游戏开发交流小组,希望大家可以点击进来一起交流一下开发经验呀! 在本文中,我们将详细介绍如何搭建Unity…...
.init(root)的作用)
Python笔记-super().init(root)的作用
假设我们有一个名为Animal的父类,它有一个属性color,在其构造函数__init__中被初始化: class Animal:def __init__(self, color):self.color color现在,我们想创建一个Animal的子类,名为Dog。Dog类有自己的属性name&…...
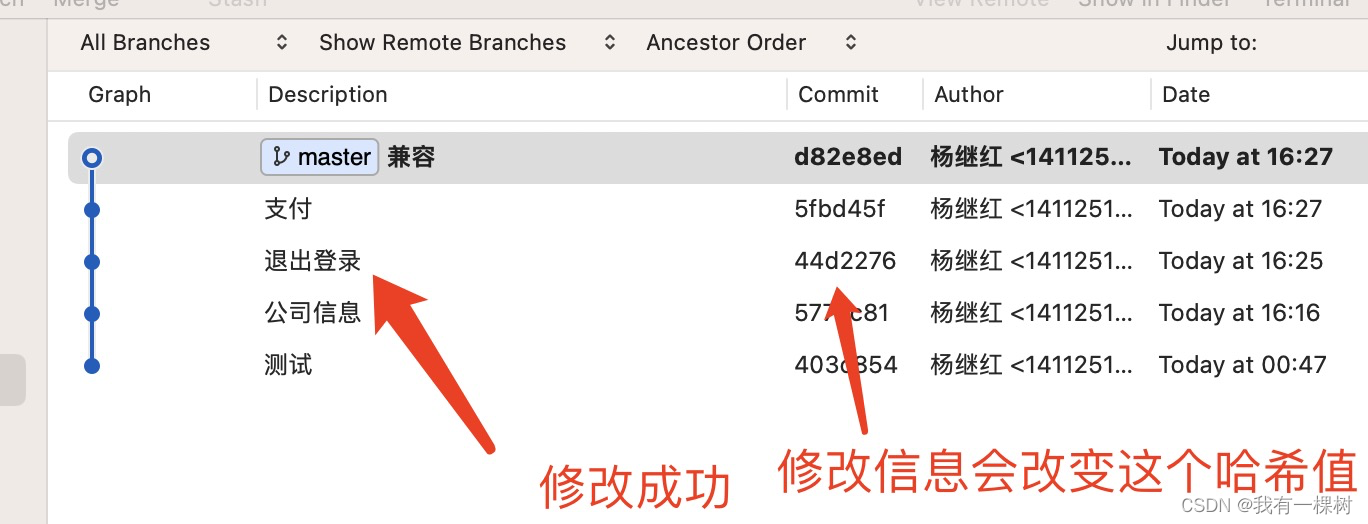
【git 使用】使用 git rebase -i 修改任意的提交信息/合并多个提交
修改最近一次的提交信息的方法有很多,可以参考这篇文章,但是对于之前的提交信息进行修改只能使用 rebase。 修改提交信息 假设我们想修改下面这个提交信息,想把【登录】改成【退出登录】步骤如下 运行 git rebase -i head~3 打开了一个文本…...

【Vue3】toRefs和toRef在reactive中的一些应用
💗💗💗欢迎来到我的博客,你将找到有关如何使用技术解决问题的文章,也会找到某个技术的学习路线。无论你是何种职业,我都希望我的博客对你有所帮助。最后不要忘记订阅我的博客以获取最新文章,也欢…...
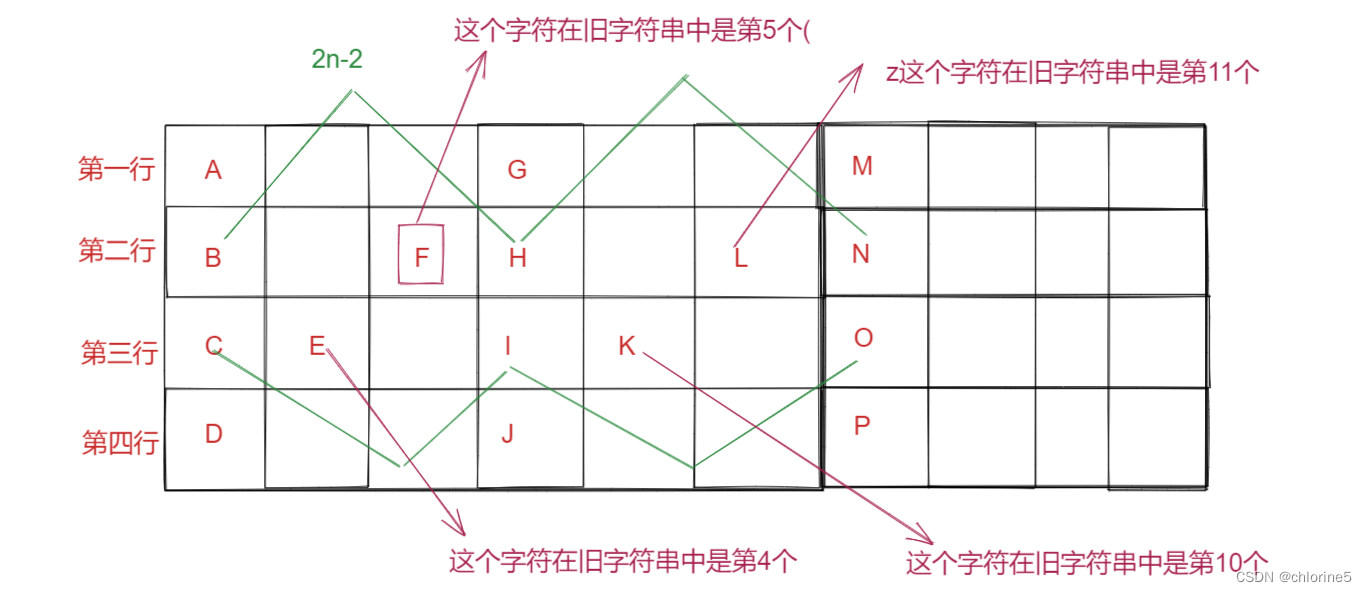
力扣精选算法100道——Z字形变换(模拟专题)
目录 🎈了解题意 🎈算法原理 🚩先处理第一行和最后一行 🚩再处理中间行 🎈实现代码 🎈了解题意 大家看到这个题目的时候肯定是很迷茫的,包括我自己也是搞不清楚题目什么意思,我…...
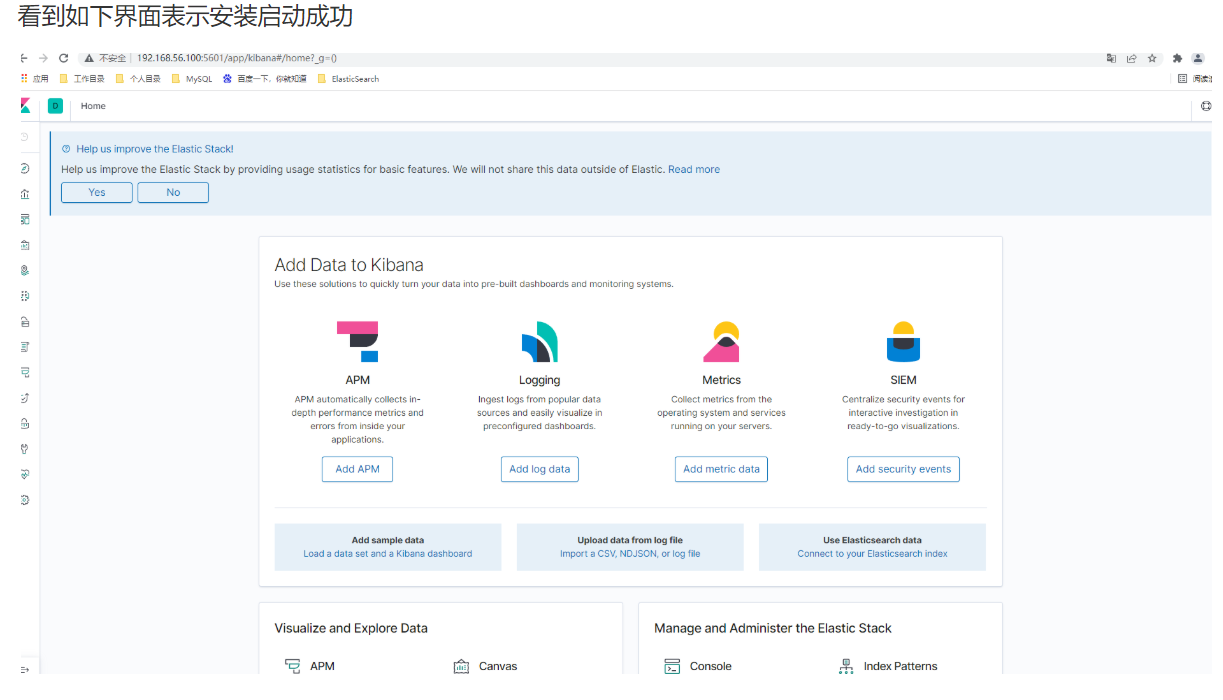
Elastic Stack--01--简介、安装
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1. Elastic Stack 简介为什么要学习ESDB-Engines搜索引擎类数据库排名常年霸榜
.NET项目web自动化测试实战——Selenium 2.0
🔥 交流讨论:欢迎加入我们一起学习! 🔥 资源分享:耗时200小时精选的「软件测试」资料包 🔥 教程推荐:火遍全网的《软件测试》教程 📢欢迎点赞 👍 收藏 ⭐留言 …...

【Day53】代码随想录之动态规划_买卖股票ⅠⅡ
文章目录 动态规划理论基础动规五部曲:出现结果不正确: 1. 买卖股票的最佳时机2. 买卖股票的最佳时机Ⅱ 动态规划理论基础 动规五部曲: 确定dp数组 下标及dp[i] 的含义。递推公式:比如斐波那契数列 dp[i] dp[i-1] dp[i-2]。初…...
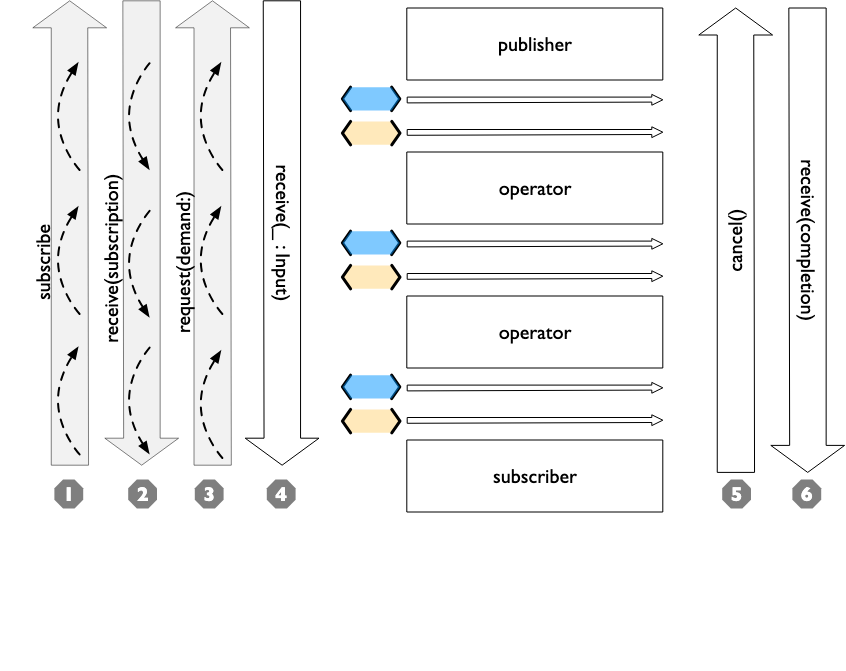
Swift Combine 使用调试器调试管道 从入门到精通二十六
Combine 系列 Swift Combine 从入门到精通一Swift Combine 发布者订阅者操作者 从入门到精通二Swift Combine 管道 从入门到精通三Swift Combine 发布者publisher的生命周期 从入门到精通四Swift Combine 操作符operations和Subjects发布者的生命周期 从入门到精通五Swift Com…...

go内置库函数实现client与server数据的发送接收
功能:客户端持续写入数据,直到输入exit退出,服务端读取数据并打印 注意:server和client目录在同一层级 服务端 server/main package mainimport ("fmt""net" )func main() {listen, err : net.Listen(&quo…...
[java基础揉碎]this
引出this: 什么是this: java虚拟机会给每个对象分配 this,代表当前对象。 这里的this就是new出来的这个对象 this的本质: this是个引用在堆中指向它自己: this的细节: 访问成员方法: 访问构造器:...

vulnhub靶场之Deathnote
一.环境搭建 1.靶场描述 Level - easy Description : dont waste too much time thinking outside the box . It is a Straight forward box . This works better with VirtualBox rather than VMware 2.靶场下载 https://www.vulnhub.com/entry/deathnote-1,739/ 3.启动环…...

Docker安装Postgresql12
1、搜索仓库中postgres docker search postgres 2、拉取镜像 docker pull postgres docker pull postgres:12 #拉取12版本的PG库 3、创建数据库文件夹 cd /temp/ && mkdir -m 755 postgres-data 注:-m表示权限,类chmod命令 4、执行命令启动…...

服务器防火墙的应用技术有哪些类型?
随着互联网的发展,网络安全问题更加严峻。服务器防火墙技术作为一种基础的网络安全技术,对于保障我们的网络安全至关重要。本文将介绍服务器防火墙的概念和作用,以及主要的服务器防火墙技术,包括数据包过滤、状态检测、代理服务、…...

IP地理位置查询定位:技术原理与实际应用
在互联网时代,IP地址是连接世界的桥梁,而了解IP地址的地理位置对于网络管理、个性化服务以及安全监控都至关重要。IP数据云将深入探讨IP地理位置查询定位的技术原理、实际应用场景以及相关的隐私保护问题,旨在为读者提供全面了解和应用该技术…...

hbuilder运行不了php文件是什么原因?
如果 HBuilder 无法运行 PHP 文件,可能是由于以下几个常见原因导致的: 未安装 PHP 解释器: HBuilder 需要安装 PHP 解释器才能运行 PHP 文件。请确保您的系统中已经安装了 PHP,并且已正确配置了环境变量。 PHP 解释器路径错误&…...
)
C++从入门到精通 第十六章(STL常用算法)
写在前面: 本系列专栏主要介绍C的相关知识,思路以下面的参考链接教程为主,大部分笔记也出自该教程,笔者的原创部分主要在示例代码的注释部分。除了参考下面的链接教程以外,笔者还参考了其它的一些C教材(比…...
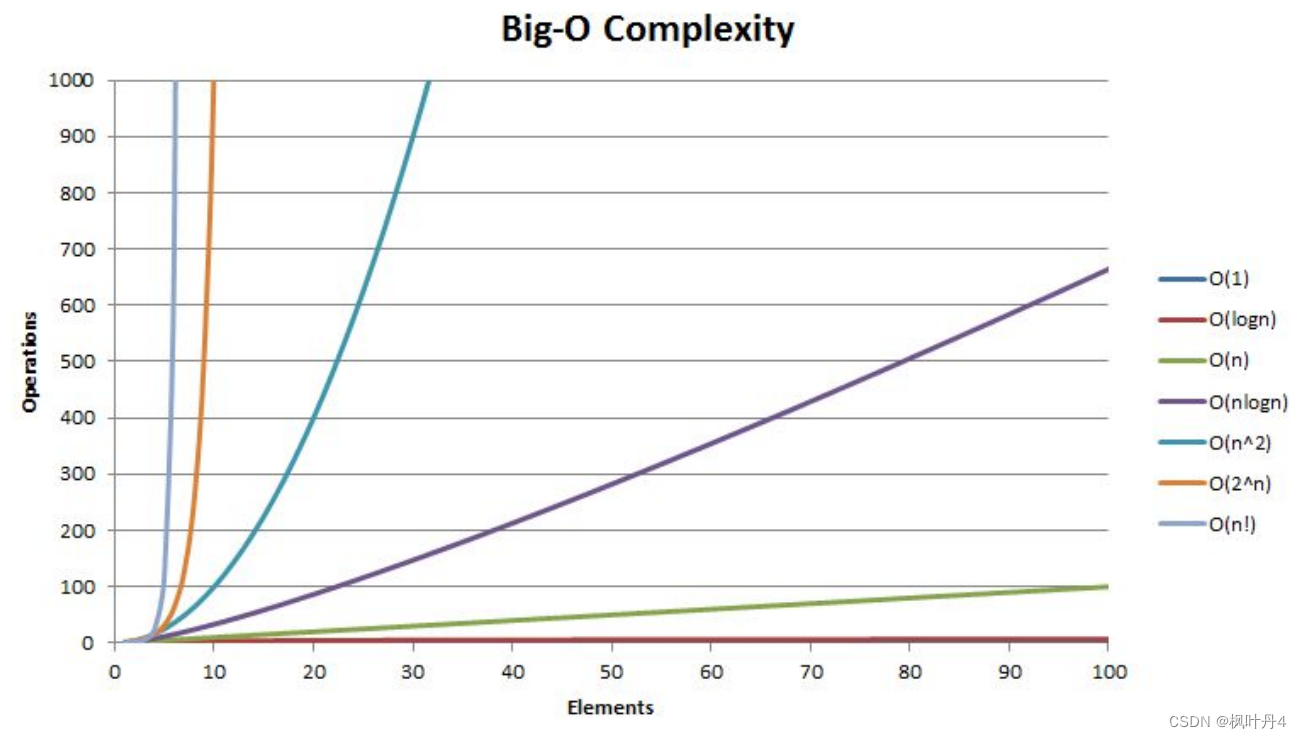
【海贼王的数据航海:利用数据结构成为数据海洋的霸主】时间复杂度 | 空间复杂度
目录 1 -> 算法效率 1.1 -> 如何衡量一个算法的好坏? 1.2 -> 算法的复杂度 2 -> 时间复杂度 2.1 -> 时间复杂度的概念 2.2 -> 大O的渐进表示法 2.3 -> 常见时间复杂度计算 3 -> 空间复杂度 4 -> 常见复杂度对比 1 -> 算法效…...

OpenTiny Vue 组件库适配微前端可能遇到的4个问题
本文由体验技术团队 TinyVue 项目成员岑灌铭同学创作。 前言 微前端是一种多个团队通过独立发布功能的方式来共同构建现代化 web 应用的技术手段及方法策略,每个应用可以选择不同的技术栈,独立开发、独立部署。 TinyVue组件库的跨技术栈能力与微前端十…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
