二叉树基础知识总结
目录
二叉树基础知识
概念 :
根节点的五个形态 :
特殊的二叉树
满二叉树 :
完全二叉树 :
二叉搜索树 :
平衡二叉搜索树 :
二叉树的性质 :
二叉树的存储结构
二叉树的顺序存储结构
二叉树的链式存储结构
二叉树的遍历方式 :
基础概念
前中后遍历
层序遍历 :
二叉树基础知识
概念 :
二叉树(binary tree)是指树中节点的度不大于2的有序树,它是一种最简单且最重要的树。二叉树的递归定义为:二叉树是一棵空树,或者是一棵由一个根节点和两棵互不相交的,分别称作根的左子树和右子树组成的非空树;左子树和右子树又同样都是二叉树。
根节点的五个形态 :
-
空二叉树
-
只有一个根结点
-
根结点只有左子树
-
根结点只有右子树
-
根结点既有左子树又有右子树
特殊的二叉树
满二叉树 :
概念 :
如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。
图例 :

完全二叉树 :
概念 :
在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层(h从1开始),则该层包含 1~ 2^(h-1) 个节点。
图例 :

而

这个就不是一颗完全二叉树!
二叉搜索树 :
前面介绍的树,都没有数值的,而二叉搜索树是有数值的了,二叉搜索树是一个有序树。
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树
下面的就是一颗二叉搜索树;

二叉搜索树最大的特点就是左<父<右 ;
平衡二叉搜索树 :
又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
其中c++中的map、set、multimap,multiset的底层实现都是平衡二叉搜索树,所以map、set的增删操作时间时间复杂度是logn , 而unordered_map、unordered_set,unordered_map、unordered_set底层实现是哈希表。
二叉树的性质 :
-
二叉树的第i层上至多有2 ^ (i-1)(i≥1)个节点。
-
深度为h的二叉树中至多含有2^h-1个节点
-
若在任意一棵二叉树中,有 n0 个叶子节点,有 n2 个度为2的节点,则必有n0 = n2 + 1
-
具有n个节点的完全二叉树深为log2(x) + 1(其中x表示不大于n的最大整数)
-
若对一棵有n个节点的完全二叉树进行顺序编号(1<=i<=n),那么,对于编号为i(i>=1)的节点:
⑴i =1 时,该节点为根,它无双亲节点 。
⑵ i > 1 时,该节点的双亲节点的编号为i/2 。
⑶2i<= n,则有编号为2i的左节点,否则没有左节点 。
⑷2i+1<=n ,则有编号为2i+1的右节点,否则没有右节点 。
二叉树的存储结构
二叉树可以顺序存储,也可以链式存储 ;
二叉树的顺序存储结构
二叉树的顺序存储结构就是用一维数组存储二叉树中的结点,并且结点的存储位置,也就是数组的下标要能体现结点之间的逻辑关系,比如双亲与孩子的关系,左右兄弟的关系等。
如以下这颗完全二叉树 :

可以采用以下线性表来存储:
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 数据 | A | B | C | D | E | F | G | H | I | J |
如果父节点的数组下标是 i,那么它的左孩子就是 i * 2 + 1,右孩子就是 i * 2 + 2。
二叉树的链式存储结构
在链式结构中,一个二叉树的结点包含左孩子指针,数据,右孩子指针 ;

链式存储效果如图 :
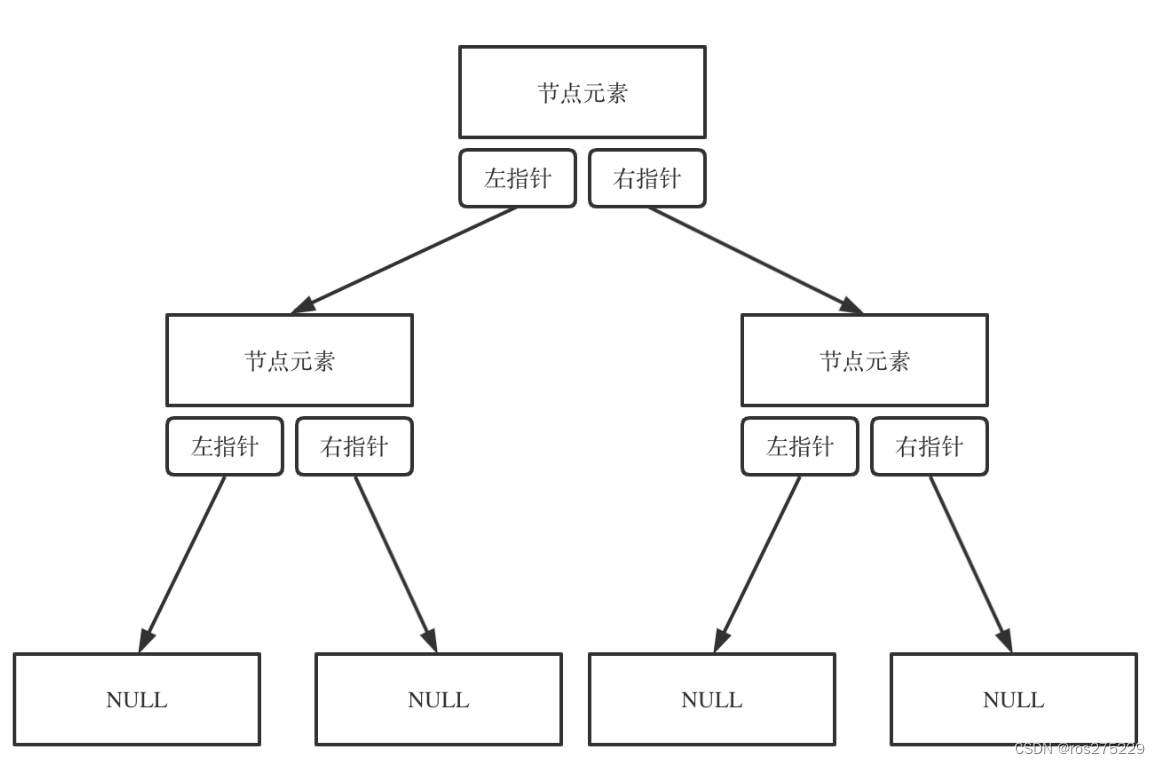
二叉链表的结构体定义 :
typedef struct BiTNode
{TElemType data; //数据域struct BiTNode *lchild,*rchild; //指针域
}BiTNode,*BiTree;二叉树的遍历方式 :
基础概念
首先,主要的两种遍历方式为 :
- 深度优先遍历:先往深走,遇到叶子节点再往回走。
- 广度优先遍历:一层一层的去遍历。
这两种遍历方法又可以细分 :
- 深度优先遍历
- 前序遍历(递归法,迭代法)
- 中序遍历(递归法,迭代法)
- 后序遍历(递归法,迭代法)
- 广度优先遍历
- 层次遍历(迭代法)
前中后遍历
其中前中后三种结点的遍历顺序 如下 :
- 前序遍历:中左右
- 中序遍历:左中右
- 后序遍历:左右中
图例 :

层序遍历 :
从树的第一层开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问 ;
如下图 :
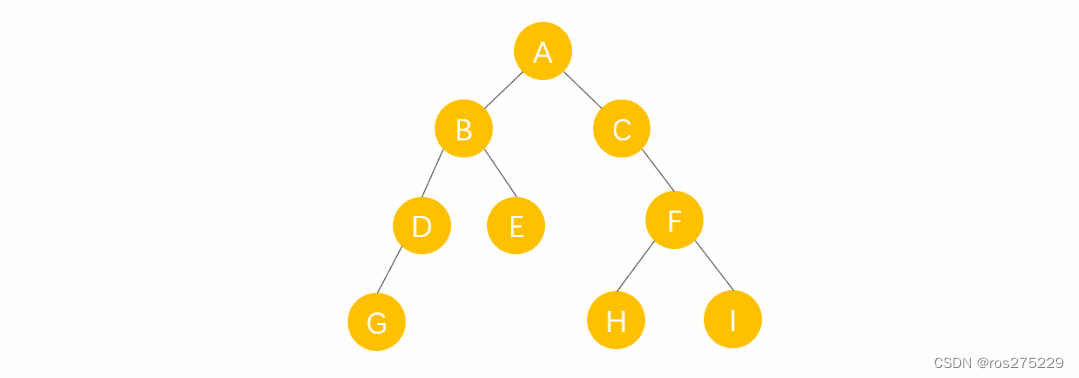
层序遍历的结果为 :
ABCDEFGHI
参考 :
-
《大话数据结构》
-
《数据结构》C语言版(清华严蔚敏考研版)
-
【数据结构与算法】二叉树
-
代码随想录
相关文章:

二叉树基础知识总结
目录 二叉树基础知识 概念 : 根节点的五个形态 : 特殊的二叉树 满二叉树 : 完全二叉树 : 二叉搜索树 : 平衡二叉搜索树 : 二叉树的性质 : 二叉树的存储结构 二叉树的顺序存储结构 二叉树的链式存储结构 二叉树的遍历方式 : 基础概念 前中后遍历 层序遍历 :…...

IDEA2023.3.4开启SpringBoot项目的热部署【简单明了4步操作】
添加devtools依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-devtools</artifactId><scope>runtime</scope><optional>true</optional> </dependency>IDEA开启自动编译 …...

QT中调用python
一.概述 1.Python功能强大,很多Qt或者c/c开发不方便的功能可以由Python编码开发,尤其是一些算法库的应用上,然后Qt调用Python。 2.在Qt调用Python的过程中,必须要安装python环境,并且Qt Creator中编译器与Python的版…...
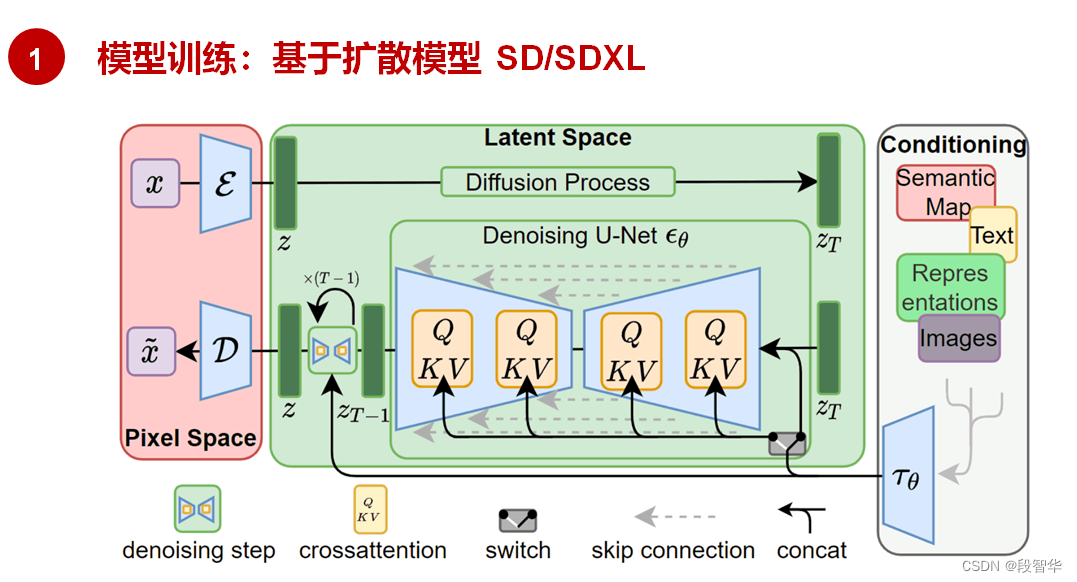
Sora基础知识学习
...

开源博客项目Blog .NET Core源码学习(9:Autofac使用浅析)
开源博客项目Blog使用Autofac注册并管理组件和服务,Autofac是面向.net 的开源IOC容器,支持通过接口、实例、程序集等方式注册组件和服务,同时支持属性注入、方法注入等注入方式。本文学习并记录Blog项目中Autofac的使用方式。 整个Blog解…...

Go语言中的TLS加密:深入crypto/tls库的实战指南
Go语言中的TLS加密:深入crypto/tls库的实战指南 引言crypto/tls库的核心组件TLS配置:tls.Config证书加载与管理TLS握手过程及其实现 构建安全的服务端创建TLS加密的HTTP服务器配置TLS属性常见的安全设置和最佳实践 开发TLS客户端应用编写使用TLS的客户端…...
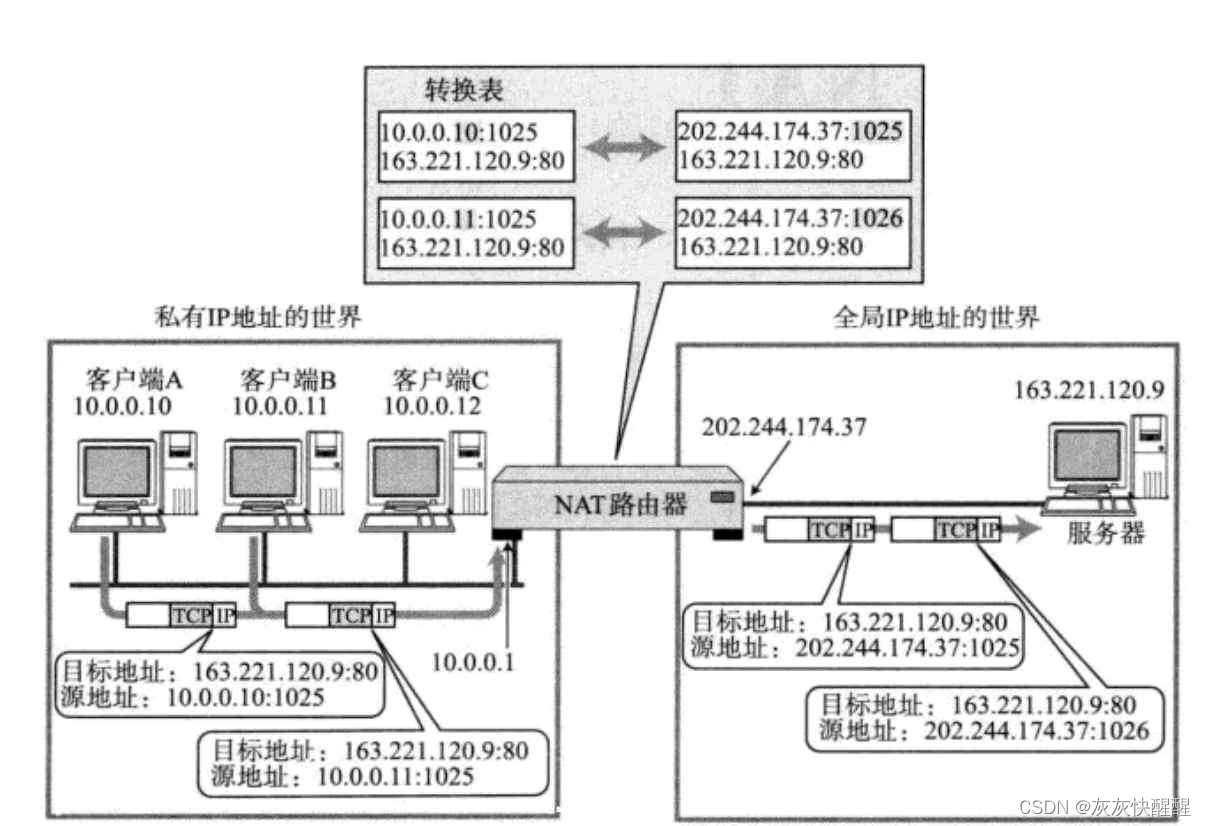
网络原理-TCP/IP(7)
目录 网络层 路由选择 数据链路层 认识以太网 以太网帧格式 认识MAC地址 对比理解MAC地址和IP地址 认识MTU ARP协议 ARP协议的作用 ARP协议工作流程 重要应用层协议DNS(Domain Name System) DNS背景 NAT技术 NAT IP转换过程 NAPT NAT技术的优缺点 网络层 路由…...
HarmonyOS4.0系列——08、整合UI常用组件
HarmonyOS4.0 系列——08、UI 组件 Blank Blank 组件在横竖屏占满空余空间效果 // xxx.ets Entry Component struct BlankExample {build() {Column() {Row() {Text(Button).fontSize(18)Blank()Toggle({type: ToggleType.Switch}).margin({top: 14,bottom: 14,left: 6,righ…...

【Spring Boot 3】【JPA】一对多单向关联
【Spring Boot 3】【JPA】一对多单向关联 背景介绍开发环境开发步骤及源码工程目录结构总结背景 软件开发是一门实践性科学,对大多数人来说,学习一种新技术不是一开始就去深究其原理,而是先从做出一个可工作的DEMO入手。但在我个人学习和工作经历中,每次学习新技术总是要花…...

工信部等九部门:打造一批实现制造过程数字孪生的数字化转型标杆工厂
“人工智能技术与咨询” 发布 培育一批科技领军人才、青年骨干人才,以及一批既懂原材料工业又懂数字技术的复合型人才。依托职业教育提质培优行动计划,加速培育数字化转型急需紧缺的工程师和技术技能人才。支持引进数字化转型海外高端人才。 ÿ…...
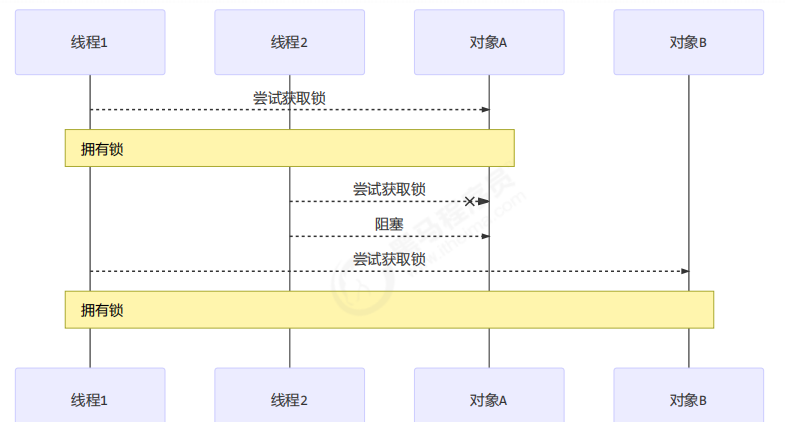
并发编程(2)基础篇-管程
4 共享模型之管程 本章内容 共享问题synchronized线程安全分析Monitorwait/notify线程状态转换活跃性Lock 4.1 共享带来的问题 4.1.1 小故事 老王(操作系统)有一个功能强大的算盘(CPU),现在想把它租出去ÿ…...

OpenAI文生视频大模型Sora概述
Sora,美国人工智能研究公司OpenAI发布的人工智能文生视频大模型(但OpenAI并未单纯将其视为视频模型,而是作为“世界模拟器” ),于2024年2月15日(美国当地时间)正式对外发布。 Sora可以根据用户…...
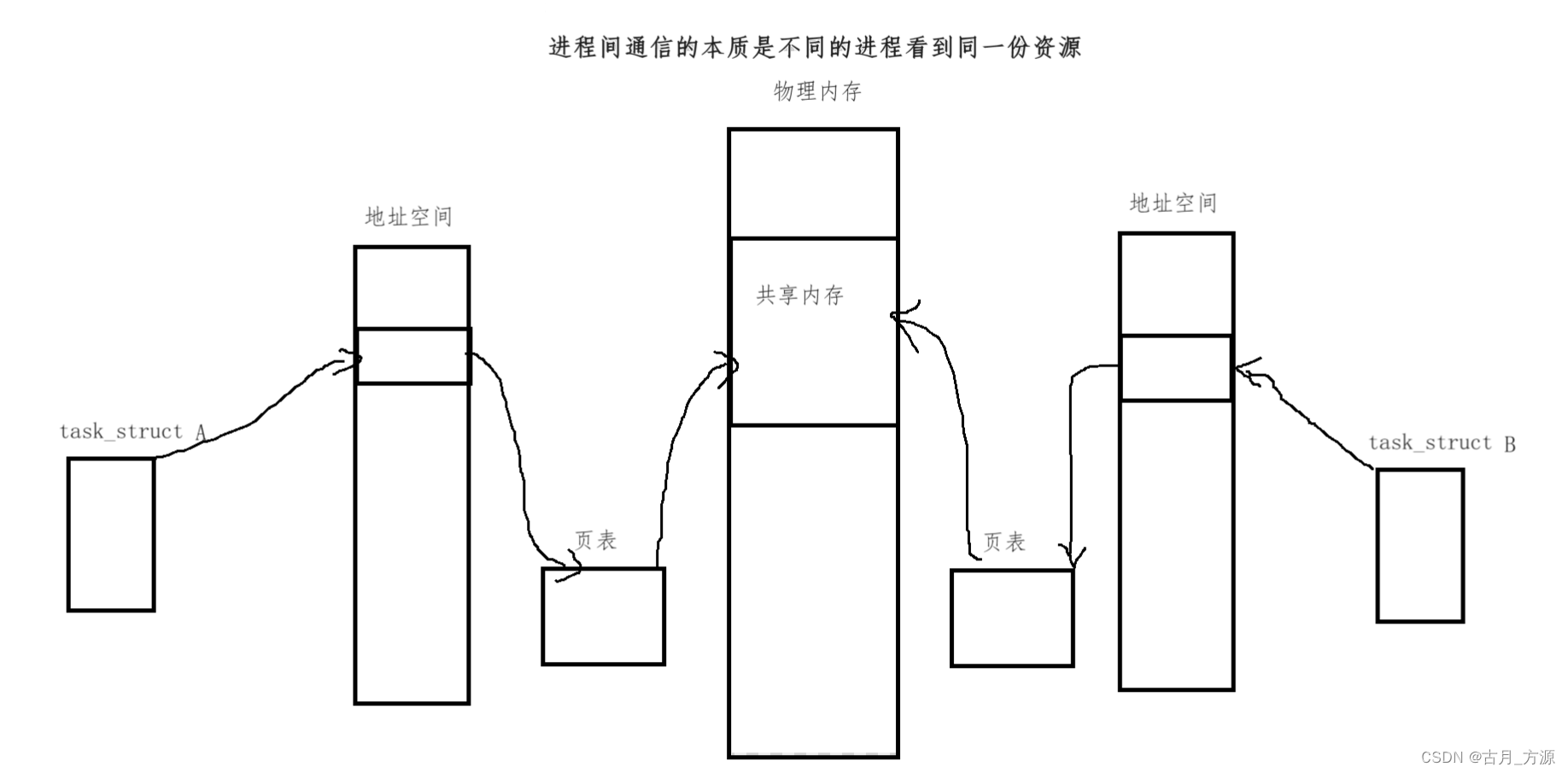
[linux]进程间通信(IPC)———共享内存(shm)(什么是共享内存,共享内存的原理图,共享内存的接口,使用演示)
一、什么是共享内存 共享内存区是最快的(进程间通信)IPC形式。一旦这样的内存映射到共享它的进程的地址空间,这些进程间数据传递不再涉及到内核,换句话说是进程不再通过执行进入内核的系统调用来传递彼此的数据。注意:…...

Go 原子操作有哪些?
Go atomic包是最轻量级的锁(也称无锁结构),可以在不形成临界区和创建互斥量的情况下完成并发安全的值替换操作,不过这个包只支持int32/int64/uint32/uint64/uintptr这几种数据类型的一些基础操作(增减、交换、载入、存…...
爬虫知识--02
免费代理池搭建 # 代理有免费和收费代理 # 代理有http代理和https代理 # 匿名度: 高匿:隐藏访问者ip 透明:服务端能拿到访问者ip 作为后端,如何拿到使用代理人的ip 请求头中:x-forwor…...

SCI一区 | Matlab实现GAF-PCNN-MSA格拉姆角场和双通道PCNN融合注意力机制的多特征分类预测
SCI一区 | Matlab实现GAF-PCNN-MSA格拉姆角场和双通道PCNN融合注意力机制的多特征分类预测 目录 SCI一区 | Matlab实现GAF-PCNN-MSA格拉姆角场和双通道PCNN融合注意力机制的多特征分类预测效果一览基本介绍模型描述程序设计参考资料 效果一览 基本介绍 1.【SCI一区级】Matlab实…...
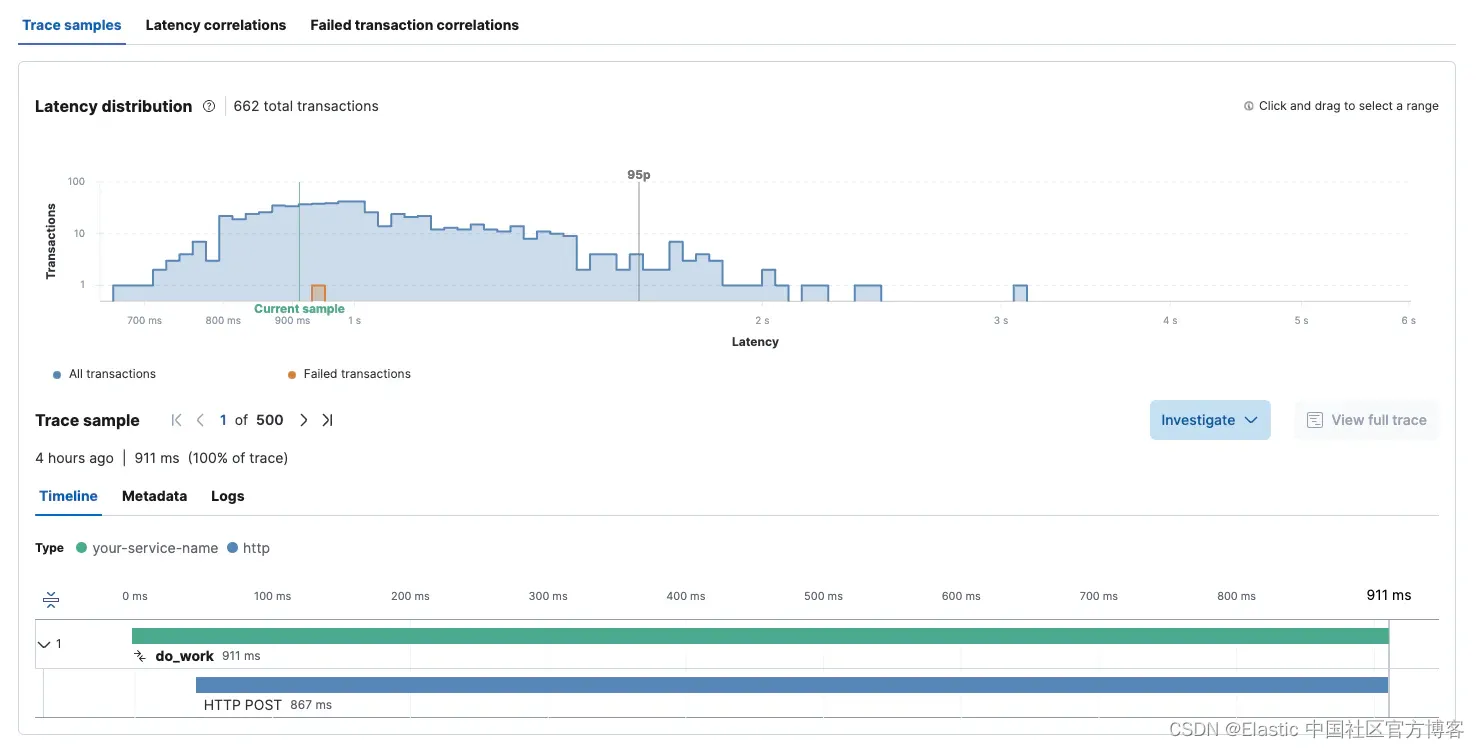
Observability:使用 OpenTelemetry 和 Elastic 监控 OpenAI API 和 GPT 模型
作者: 来自 Elastic David Hope ChatGPT 现在非常火爆,甚至席卷了整个互联网。 作为 ChatGPT 的狂热用户和 ChatGPT 应用程序的开发人员,我对这项技术的可能性感到非常兴奋。 我看到的情况是,基于 ChatGPT 的解决方案将会呈指数级…...
靡语IT:Vue精讲(一)
Vue简介 发端于2013年的个人项目,已然成为全世界三大前端框架之一,在中国大陆更是前端首选。 它的设计思想、编码技巧也被众多的框架借鉴、模仿。 纪略 2013年,在Google工作的尤雨溪,受到Angular的启发,从中提取自…...
vue3 toRefs之后的变量修改方法
上效果 修改值需要带上解构之前的对象名obj, changeName:()>{ // toRefs 解决后变量修改值方法: 解构前变量.字段新值 obj.name FEIFEI; } } 案例源码 <!DOCTYPE html> <html> <head><me…...
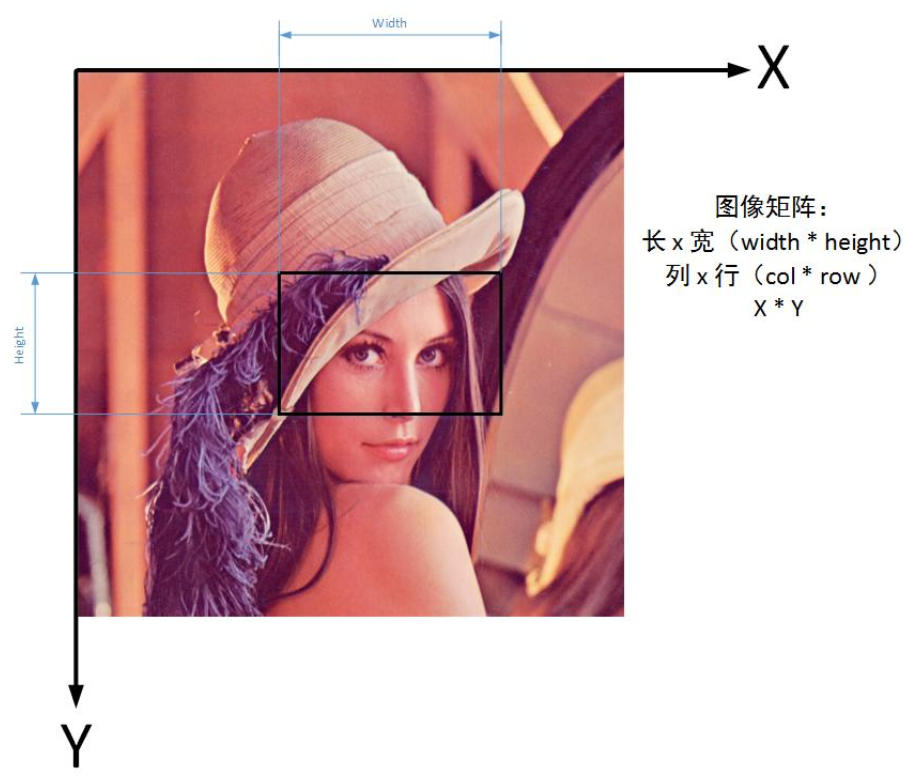
【教程】详解相机模型与坐标转换
转载请注明出处:小锋学长生活大爆炸[xfxuezhang.cn] 由于复制过来,如果有格式问题,推荐大家直接去我原网站上查看: 相机模型与坐标转换 - 生活大爆炸 目录 经纬度坐标系 转 地球直角坐标系大地直角坐标系 转 经纬度坐标系地理坐标…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
