Python机器学习17——极限学习机(ELM)
本系列基本不讲数学原理,只从代码角度去让读者们利用最简洁的Python代码实现机器学习方法。
背景:

极限学习机(ELM)也是学术界常用的一种机器学习算法,严格来说它应该属于神经网络,应该属于深度学习栏目,但是我这里把它放在了机器学习栏目里面,主要还是这个方法不是像别的神经网络一样方向传播误差去更新参数的。他是一个静态的模型 ,虽然它结构类似于多层感知机,只不过多层感知机的参数会随着迭代次数增加通过方向传播误差进行更新,而ELM不会,所以ELM的效果肯定是不如MLP的。
但是我也不知道为什么效果不好的模型学术界这么喜欢用......一堆论文不用MLP而是去用ELM....可能因为它不需要深度学习框架就可以搭建,而且运行速度快吧,门槛低,可能是不懂深度学习的人接触的最简单的神经网络实现的方法了。
sklearn库没有现成的接口调用,我们下面的ELM都是自定义的类,模仿sklearn的接口使用。
当然单纯的ELM由于它的权重矩阵都是静态的,效果不好,所以可以使用拟牛顿法或者别的梯度下降的方法根据误差去优化其参数矩阵,达到更好的效果。(说实话这不就是MLP嘛....)
下面会自定义ELM和优化的ELM两个类,还给出了一个基于优化的ELM结合ER回归的类。
(请注意我这里都是回归问题的ELM代码,分类问题还需要进行改动)
代码实现
原理就不多介绍了,别的文章都有,我直接给ELM的代码案例。本次使用一个回归问题,16的特征变量,响应变量是一个数值,使用ELM预测。
导入包,然后读取数据,取出X和y,我数据的最后一列就是y,然后给它划分训练集和测试集。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error,r2_score
plt.rcParams ['font.sans-serif'] ='SimHei' #显示中文
plt.rcParams ['axes.unicode_minus']=False #显示负号# 加载数据
data =pd.read_csv('CS2_35的特征.csv')
X = data.iloc[:,:-1]
y = data.iloc[:,-1]# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)标准化一下:
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train_s = scaler.transform(X_train)
X_test_s = scaler.transform(X_test)
print('训练数据形状:')
print(X_train_s.shape,y_train.shape)
print('测试数据形状:')
print(X_test_s.shape,y_test.shape)
自定义ELM类
class ELMRegressor():def __init__(self, n_hidden):self.n_hidden = n_hiddendef fit(self, X, y):self.X = Xself.y = yn_samples, n_features = X.shapeself.W = np.random.randn(n_features+1, self.n_hidden)H = np.dot(np.concatenate((X, np.ones((n_samples, 1))), axis=1), self.W)H = np.maximum(H, 0)self.beta = np.dot(np.linalg.pinv(H), y)def predict(self, X):n_samples = X.shape[0]H = np.dot(np.concatenate((X, np.ones((n_samples, 1))), axis=1), self.W)H = np.maximum(H, 0)y_pred = np.dot(H, self.beta)return y_pred自定义优化参数矩阵的ELM类
这里采用scipy.optimize 里面的minimize方法,使用拟牛顿法进行优化参数矩阵。
from scipy.optimize import minimize
class OP_ELMRegressor():def __init__(self, n_hidden):self.n_hidden = n_hiddendef fit(self, X, y):self.X = Xself.y = yn_samples, n_features = X.shapeself.W = np.random.randn(n_features + 1, self.n_hidden)def loss_func(W_vec):W = W_vec.reshape((n_features + 1, self.n_hidden))H = np.dot(np.hstack((X, np.ones((n_samples, 1)))), W)H = np.maximum(H, 0)beta = np.dot(np.linalg.pinv(H), y)y_pred = np.dot(H, beta)mse = np.mean((y - y_pred) ** 2)return mse# 用拟牛顿法优化权重矩阵res = minimize(loss_func, self.W.ravel(), method='BFGS')self.W = res.x.reshape((n_features + 1, self.n_hidden))H = np.hstack((X, np.ones((n_samples, 1)))) # 添加偏置项H = np.dot(H, self.W)H = np.maximum(H, 0)self.beta = np.dot(np.linalg.pinv(H), y)def predict(self, X):n_samples = X.shape[0]H = np.hstack((X, np.ones((n_samples, 1))))H = np.dot(H, self.W)H = np.maximum(H, 0)y_pred = np.dot(H, self.beta)return y_pred自定义优化参数矩阵的ELM结合ER回归的类
不懂什么是ER回归可以去搜一下....核心改动就是损失函数改了,不是MSE损失,而是ER损失。总之这是一种机器学习结合统计学的方法,算得上创新。
class OP_ELMRegressor_ER():def __init__(self, n_hidden,tau):self.n_hidden = n_hiddenself.tau = taudef fit(self, X, y):self.X = Xself.y = yn_samples, n_features = X.shapeself.W = np.random.randn(n_features + 1, self.n_hidden)def loss_func(W,tau=self.tau):W = W.reshape((n_features + 1, self.n_hidden))H = np.dot(np.hstack((X, np.ones((n_samples, 1)))), W)H = np.maximum(H, 0)beta = np.dot(np.linalg.pinv(H), y)y_pred = np.dot(H, beta)loss=np.mean(np.where(np.greater(y,y_pred),np.power((y-y_pred),2)*tau,np.power((y-y_pred),2)*(1-tau)))return loss# 用拟牛顿法优化权重矩阵res = minimize(loss_func, self.W.ravel(), method='BFGS')self.W = res.x.reshape((n_features + 1, self.n_hidden))H = np.hstack((X, np.ones((n_samples, 1)))) # 添加偏置项H = np.dot(H, self.W)H = np.maximum(H, 0)self.beta = np.dot(np.linalg.pinv(H), y)def predict(self, X):n_samples = X.shape[0]H = np.hstack((X, np.ones((n_samples, 1))))H = np.dot(H, self.W)H = np.maximum(H, 0)y_pred = np.dot(H, self.beta)return y_pred
导入别的模型对比
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import ElasticNet
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.svm import SVR
from sklearn.neural_network import MLPRegressor定义评价函数,这里计算MAE,RMSE,MAPE,R2来评价预测效果。
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error,r2_scoredef evaluation(y_test, y_predict):mae = mean_absolute_error(y_test, y_predict)mse = mean_squared_error(y_test, y_predict)rmse = np.sqrt(mean_squared_error(y_test, y_predict))mape=(abs(y_predict -y_test)/ y_test).mean()r_2=r2_score(y_test, y_predict)return mae, rmse, mape,r_2 #mse生成11个模型类的实例化,装入列表。
#线性回归
model1 = LinearRegression()#弹性网回归
model2 = ElasticNet(alpha=0.05, l1_ratio=0.5)#K近邻
model3 = KNeighborsRegressor(n_neighbors=10)#决策树
model4 = DecisionTreeRegressor(random_state=77)#随机森林
model5= RandomForestRegressor(n_estimators=500, max_features=int(X_train.shape[1]/3) , random_state=0)#梯度提升
model6 = GradientBoostingRegressor(n_estimators=500,random_state=123)#支持向量机
model7 = SVR(kernel="rbf")#神经网络
model8 = MLPRegressor(hidden_layer_sizes=(64,40), random_state=77, max_iter=10000)#MLE
model9=ELMRegressor(32)#优化MLE
model10=OP_ELMRegressor(16)#优化MLE_ER
model11=OP_ELMRegressor_ER(16,tau=0.5)model_list=[model1,model2,model3,model4,model5,model6,model7,model8,model9,model10,model11]
model_name=['线性回归','惩罚回归','K近邻','决策树','随机森林','梯度提升','支持向量机','神经网络','极限学习机','优化极限学习机','优化极限学习机+ER']训练,评价,计算误差指标
df_eval=pd.DataFrame(columns=['MAE','RMSE','MAPE','R2'])
for i in range(len(model_list)):model_C=model_list[i]name=model_name[i]print(f'{name}正在训练...')model_C.fit(X_train_s, y_train)pred=model_C.predict(X_test_s)s=evaluation(y_test,pred)df_eval.loc[name,:]=list(s)
查看:
df_eval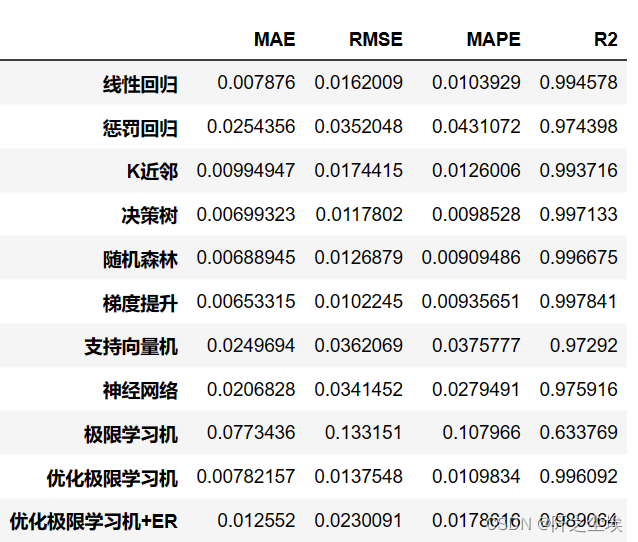
画图:
bar_width = 0.4
colors=['c', 'b', 'g', 'tomato', 'm', 'y', 'lime', 'k','orange','pink','grey','tan','purple']
fig, ax = plt.subplots(2,2,figsize=(7,5),dpi=256)
for i,col in enumerate(df_eval.columns):n=int(str('22')+str(i+1))plt.subplot(n)df_col=df_eval[col]m =np.arange(len(df_col))#hatch=['-','/','+','x'],plt.bar(x=m,height=df_col.to_numpy(),width=bar_width,color=colors)#plt.xlabel('Methods',fontsize=12)names=df_col.indexplt.xticks(range(len(df_col)),names,fontsize=8)plt.xticks(rotation=40)if col=='R2':plt.ylabel(r'$R^{2}$',fontsize=14)else:plt.ylabel(col,fontsize=14)
plt.tight_layout()
#plt.savefig('柱状图.jpg',dpi=512)
plt.show()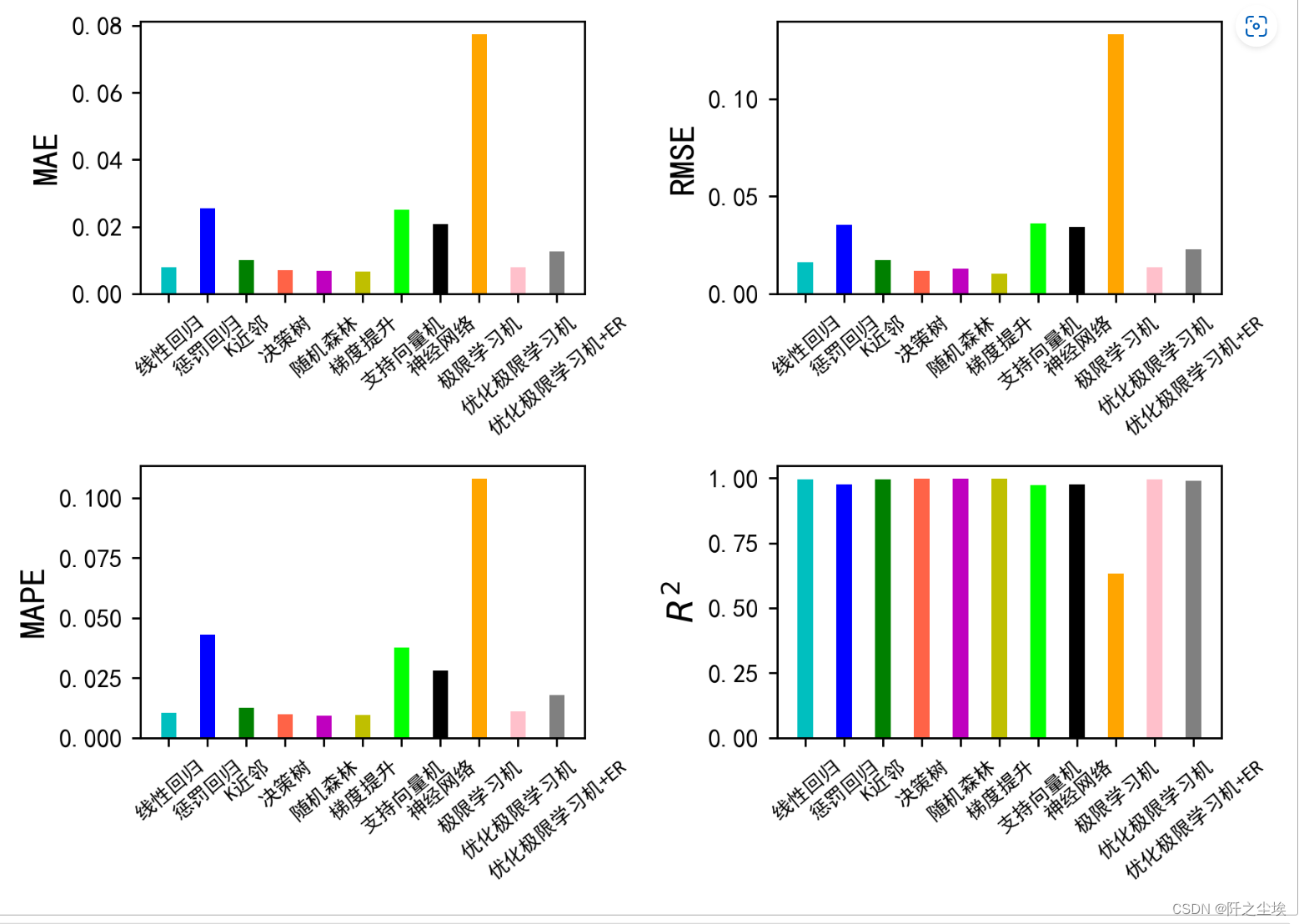
从效果上来看,这个数据集的X对y的解释能力还是很强的,线性回归的拟合优度都到了99%,所以基本模型都差不多是这个表现。单纯的ELM的表现比线性回归还差,但是用拟牛顿法优化过后效果还不错,加了ER效果也是差不多的。ER还有分位数tau这个参数可以改,说不定能出更好的效果。
整体来说是一个效果一般的机器学习模型,但是原理简单,可以很容易去改动和创新,然后发文章,所以学术界都喜欢用这个吧。。。
相关文章:

Python机器学习17——极限学习机(ELM)
本系列基本不讲数学原理,只从代码角度去让读者们利用最简洁的Python代码实现机器学习方法。 背景: 极限学习机(ELM)也是学术界常用的一种机器学习算法,严格来说它应该属于神经网络,应该属于深度学习栏目,但是我这里把它…...
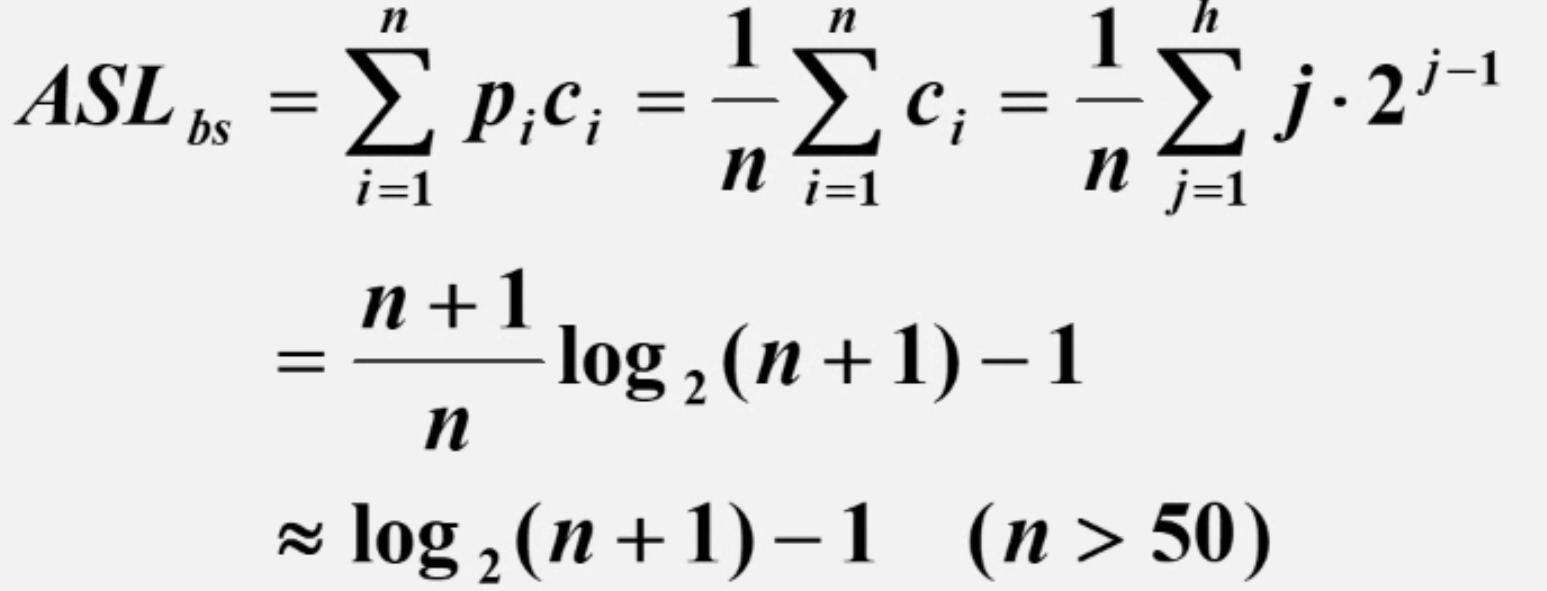
二分查找与判定树
二分查找的算法思想二分查找也称“折半查找”,要求查找表为采用顺序存储结构的有序表。本例一律采用升序排列。二分查找每一次都会比较给定值与序列[low,high]的中间元素,该元素的下标为mid (lowhigh)/2,若两者相等,则返回元素的下标为mid;如…...
反转链表(精美图示详解哦)
全文目录引言反转链表题目描述与思路实现总结引言 在学习了单链表的相关知识后,尝试实现一些题目可以帮助我们更好的理解单链表的结构以及对其的使用。 从这篇文章开始,将会介绍一些编程题来帮助我们更好的掌握单链表: 分别是反转链表、链表…...

深入理解多线程
一、线程基本概念 1、概述 线程是允许应用程序并发的一种机制。线程共享进程内的所有资源。 线程是调度的基本单位。 每个线程都有自己的 errno。 所有 pthread 函数均以返回 0 表示成功,返回一个正值表示失败。 编译 pthread 程序需要添加链接库(…...
)
华为OD机试题 - 英文输入法(JavaScript)
更多题库,搜索引擎搜 梦想橡皮擦华为OD 👑👑👑 更多华为OD题库,搜 梦想橡皮擦 华为OD 👑👑👑 更多华为机考题库,搜 梦想橡皮擦华为OD 👑👑👑 华为OD机试题 最近更新的博客使用说明本篇题解: 英文输入法题目输入输出示例一输入输出说明示例一输入输出Code…...

64 云原生容器化
文章目录 一、什么是rancher二、为什么使用rancher三、 Rancher与[k8s](https://so.csdn.net/so/search?q=k8s&spm=1001.2101.3001.7020)的关系及区别1、Rancher具有的优势三、rancher安装1、细部介绍四、图形化操作1、执行2、图形化操作1、进行客户机登录rancher2、Ranch…...

IronXL for .NET 2023.2.5 Crack
关于适用于 .NET 的 IronXL 在 C# 中阅读和编辑 Excel 电子表格,无需 MS Office 或 Excel Interop。 IronXL for .NET 允许开发人员在 .NET 应用程序和网站中读取、生成和编辑 Excel(和其他电子表格文件)。您可以读取和编辑 XLS/XLSX/CSV/TS…...
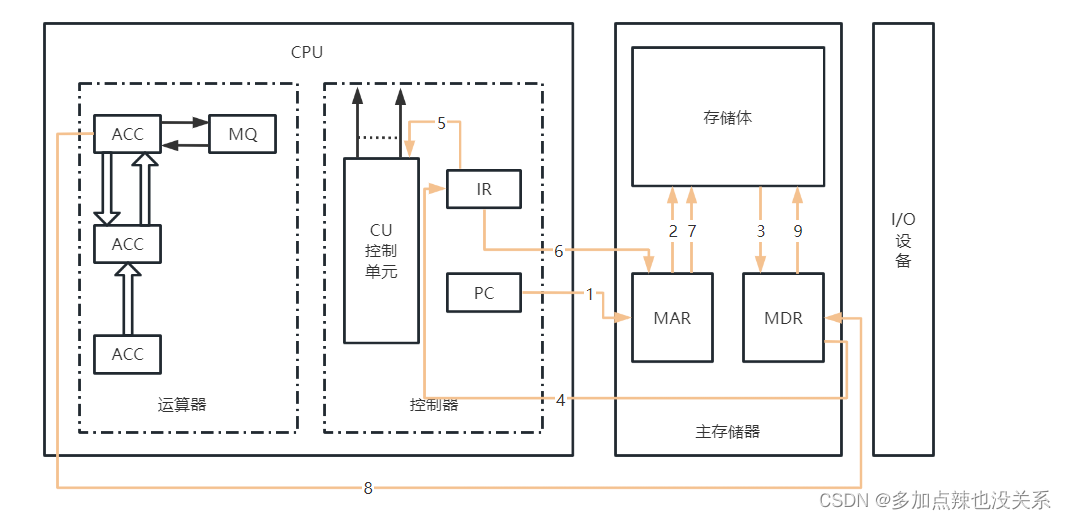
计算机组成原理|第一章(笔记)
目录第一章 计算机系统概论1.1 计算机系统简介1.1.1 计算机的软硬件概念1.1.2 计算机系统的层次结构1.1.3 计算机组成和计算机体系结构1.2 计算机的基本组成1.2.1 冯 诺伊曼计算机的特点1.2.2 计算机的硬件框图1.2.3 计算机的工作过程1.3 计算机硬件的主要技术指标1.3.1 机器字…...
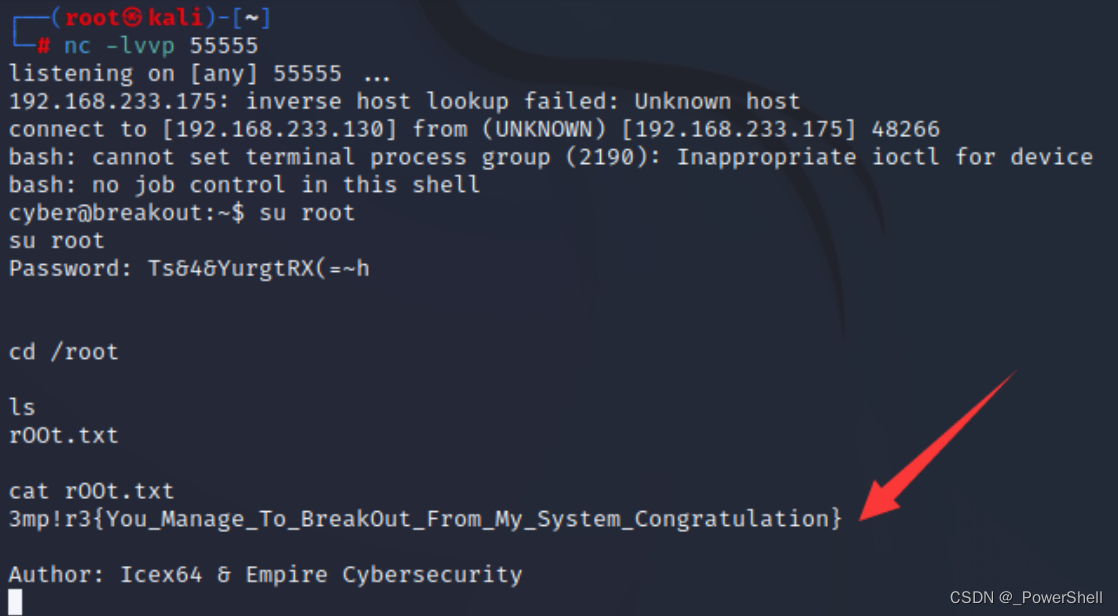
[ vulnhub靶机通关篇 ] Empire Breakout 通关详解
🍬 博主介绍 👨🎓 博主介绍:大家好,我是 _PowerShell ,很高兴认识大家~ ✨主攻领域:【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...
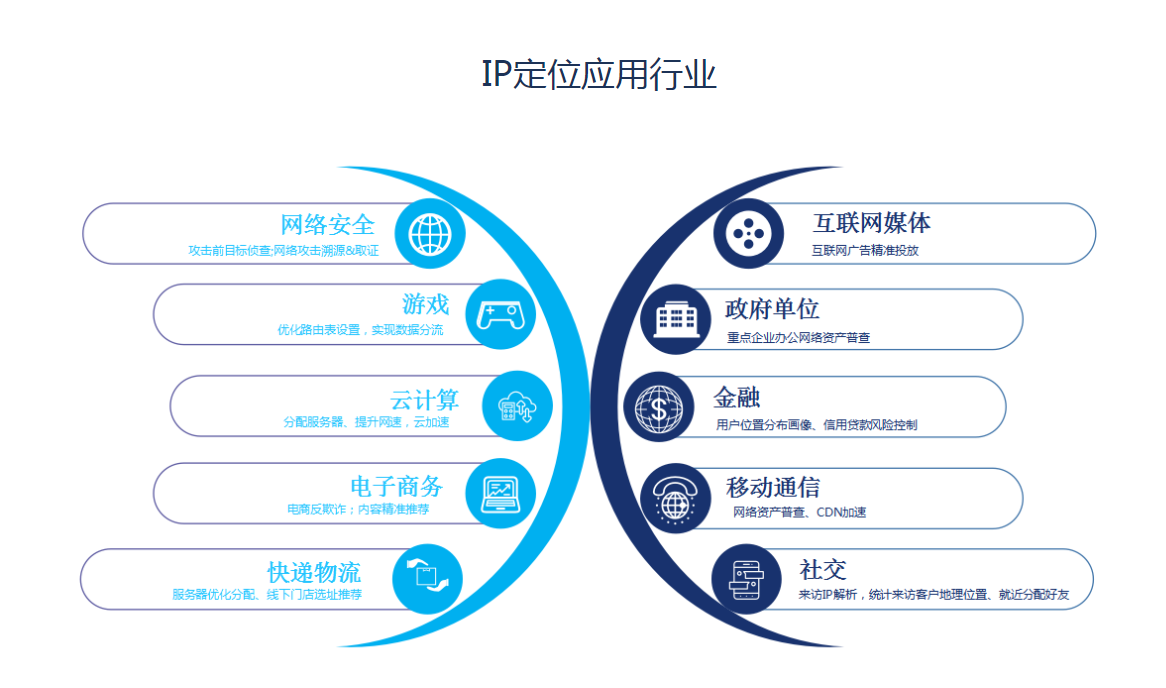
IP定位离线库有什么作用?
IP离线是什么意思?我们以丢失手机为例来寻找它,现在手机都有IP定位功能,只要手机开通了IP定位,就能找到手机。iPhone定位显示离线一般是iPhone手机关机了或者iPhone手机中“查找我的iPhone”功能关闭了。如果手机在手中的话可以打…...

[C++]vector模拟实现
目录 前言: 1. vector结构 2. 默认成员函数 2.1 构造函数 无参构造: 有参构造: 有参构造重载: 2.2 赋值运算符重载、拷贝构造(难点) 2.3 析构函数: 3. 扩容 3.1 reserve 3.2 resize…...

DevOps实战50讲-(2)Jenkins配置
1. Docker镜像方式安装拉取Jenkins镜像docker pull jenkins/jenkins编写docker-compose.ymlversion: "3.1" services:jenkins:image: jenkins/jenkinscontainer_name: jenkinsports:- 8080:8080- 50000:50000volumes:- ./data/:/var/jenkins_home/首次启动会因为数据…...
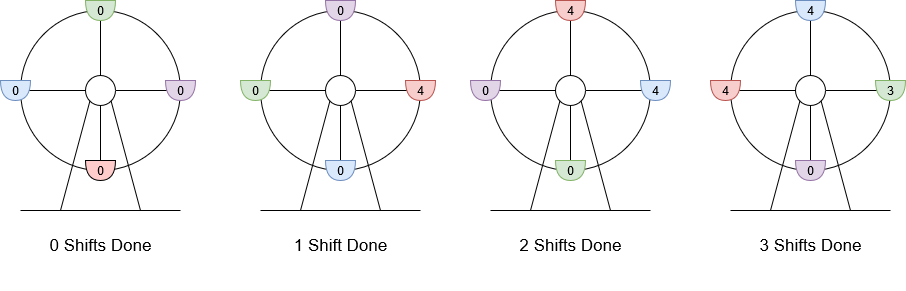
LC-1599. 经营摩天轮的最大利润(贪心)
1599. 经营摩天轮的最大利润 难度中等39 你正在经营一座摩天轮,该摩天轮共有 4 个座舱 ,每个座舱 最多可以容纳 4 位游客 。你可以 逆时针 轮转座舱,但每次轮转都需要支付一定的运行成本 runningCost 。摩天轮每次轮转都恰好转动 1 / 4 周。…...
Umi使用百度地图服务
需求描述 需要在前端页面中使用地图定位功能,所以在前端umi项目中使用百度地图服务,由于umi项目默认没有入口的html文件,所以无法通过常规的在head中加入外链js的方式使用 百度ak zyqeLCzvQPCCNImRu9yRGOqWlEUicxxGreact使用百度api 链接:…...

js中getBoundingClientRect()方法
getBoundingClientRect()返回值是一个 DOMRect 对象,是包含整个元素的最小矩形(包括 padding 和 border-width)。该对象使用 left、top、right、bottom、x、y、width 和 height 这几个以像素为单位的只读属性描述整个矩形的位置和大小。除了 …...

Unity记录2.2-动作-动画、相机、Debug与总结
文章首发及后续更新:https://mwhls.top/4453.html,无图/无目录/格式错误/更多相关请至首发页查看。 新的更新内容请到mwhls.top查看。 欢迎提出任何疑问及批评,非常感谢! 汇总:Unity 记录 摘要:重写了动画触…...

分享十个前端Web3D可视化框架附地址
Three.js:Three.js是一个流行的3D库,提供了大量的3D功能,包括基本几何形状、材质、灯光、动画、特效等。它是一个功能强大、易于使用的框架,广泛用于Web3D可视化应用程序的开发。Three.js:https://threejs.org/Babylon…...
基于WSL2和Clion搭建Win下C开发环境
系列文章目录 一、基于WSL2和Clion搭建Win下C开发环境 二、make、makeFile、CMake、CMakeLists的使用 三、全面、详细、通俗易懂的C语言语法和标准库 文章目录系列文章目录前言WSL2安装WSL常用命令VSCode连接WSLroot密码以systemd启动配置sshClion结语前言 Win下C语言开发环境…...

考研第一天,汤家凤基础班,连续与极限复习笔记
函数连续极限性质保号性证明极值点:夹逼准则二项式展开根号下,大于一,小于一的讨论直接放缩求和分子分母齐次,且分母大一次,用积分单调有界存在极限几个重要的切线放缩证明有界,然后放缩求单调证明有界&…...

聊一聊代码重构——关于变量的代码实践
提炼变量 其目标是将一个复杂表达式或语句分解成更小的部分,并将其存储在变量中。提高代码可读性和复用性 复杂的表达式 有些时候为了方便我们会把业务处理的逻辑写在一起,如果参与处理的内容较多时我们就会创造出一个非常长且难以理解的表达式。当其他…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
