2月24日(周六)比赛前瞻:曼联 VS 富勒姆、拜仁 VS 莱比锡
大家好,博主将持续更新胜负14场前瞻,此处每日赛事间歇更新,胃信号每日更新。

精选赛事:曼联 VS 富勒姆
曼联近期状态显著提升,上一轮联赛客场2-1战胜卢顿,连续7场正赛取得6胜1平的成绩,保持不败。在进攻端,曼联表现同样出色,近6场正赛持续破门,场均进球高达2.83个。然而,曼联中场范德贝克和边锋桑乔分别在冬歇期租借加盟法兰克福和德甲多特蒙德。在防守方面,曼联表现一般,近10场正赛丢了15球,场均失球1.5个。
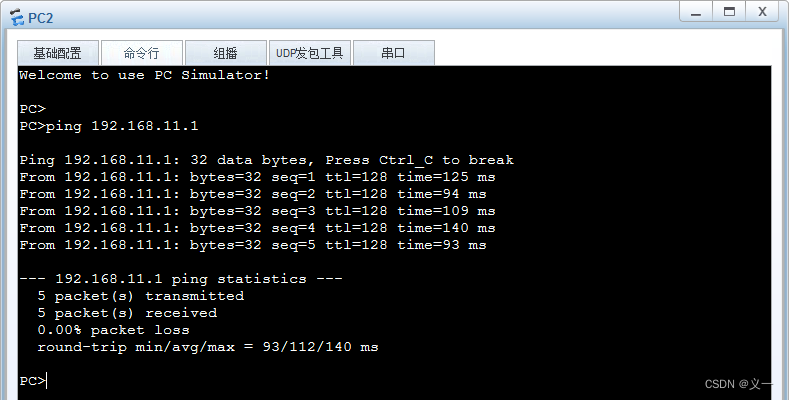
富勒姆上轮联赛主场1-2不敌阿斯顿维拉,近8场正赛仅取得1胜,状态欠佳。富勒姆近6次面对曼联1平5负,交锋劣势明显。此外,富勒姆客场表现糟糕,近10个正赛客场仅取得1胜,胜率仅为10%。
综合分析:富勒姆联赛至今12轮作客仅取得1胜4平7负的战绩,客场竞争力较弱。与此同时,曼联近期主场表现稳定,近3轮取得2胜1平的成绩,且在双方近10次交手中占据优势。因此,本场比赛富勒姆恐难逃一败。

精选赛事:拜仁慕尼黑VS莱比锡红牛
拜仁近10个正赛主场8胜1平1负,胜率高达80%,表现出色。然而,球队近期状态下滑,上轮联赛客场2-3不敌波鸿,遭遇各项赛事3连败,士气低落。此外,主力球员基米希与助教勒夫发生冲突,队内关系紧张。近期,拜仁防守质量下降,近6场正赛丢10球,场均失球1.66粒。
RB莱比锡实际状态不错,上轮联赛主场2-0战胜门兴,近4场正赛2胜1平1负,负场对手为顶级豪门皇马,表现尚可。RB莱比锡近4次对阵拜仁2胜2平,交锋优势明显。然而,球队客场能力欠佳,近10个正赛客场3胜2平5负,胜率仅30%。近期,RB莱比锡防守也有所下滑,近6场正赛丢11球,场均失球1.83粒。
综合分析:拜仁虽遭三连败,但主场表现仍可圈可点。然而,RB莱比锡近期状态有所反弹,阵容齐整,且上次做客安联竞技场表现惊艳。面对拜仁的低谷,RB莱比锡有望至少拿分。

昨日回顾:
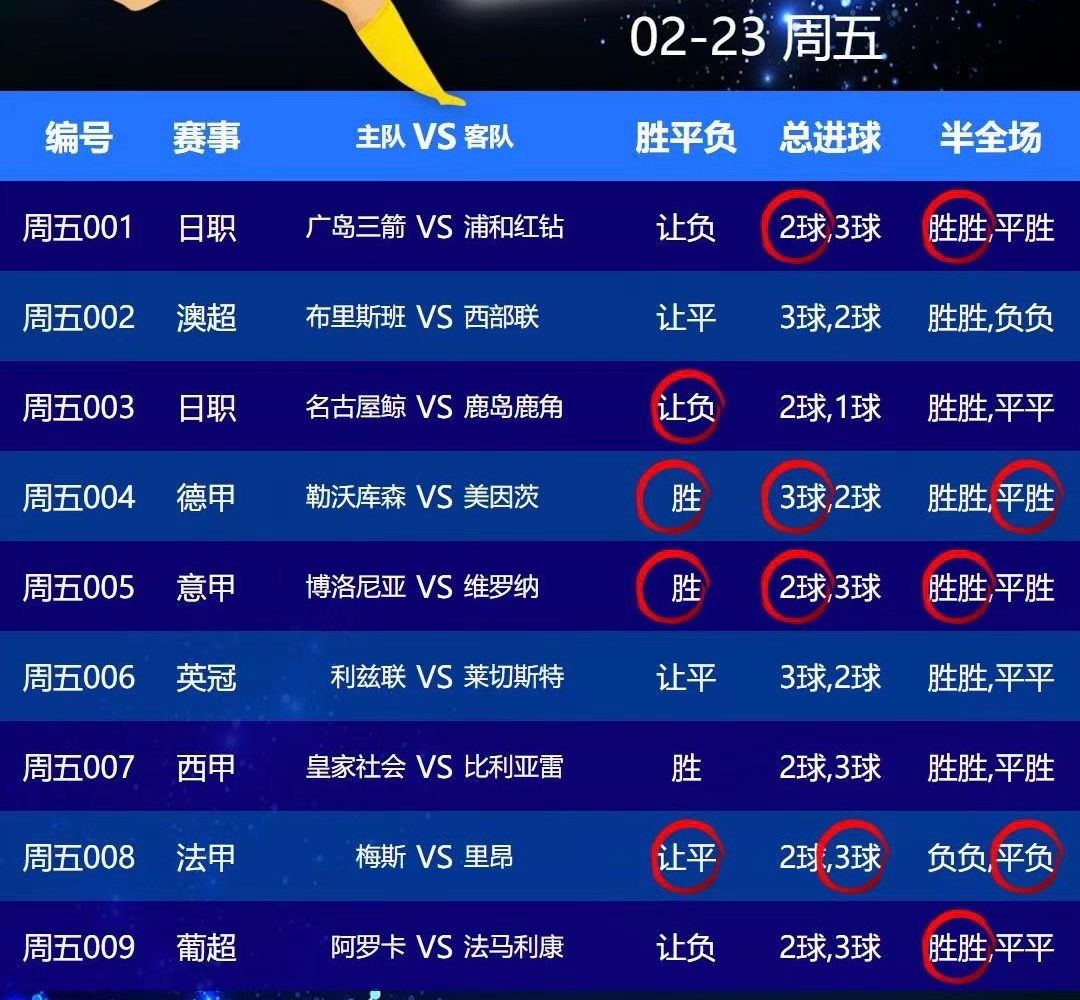
今日数据:
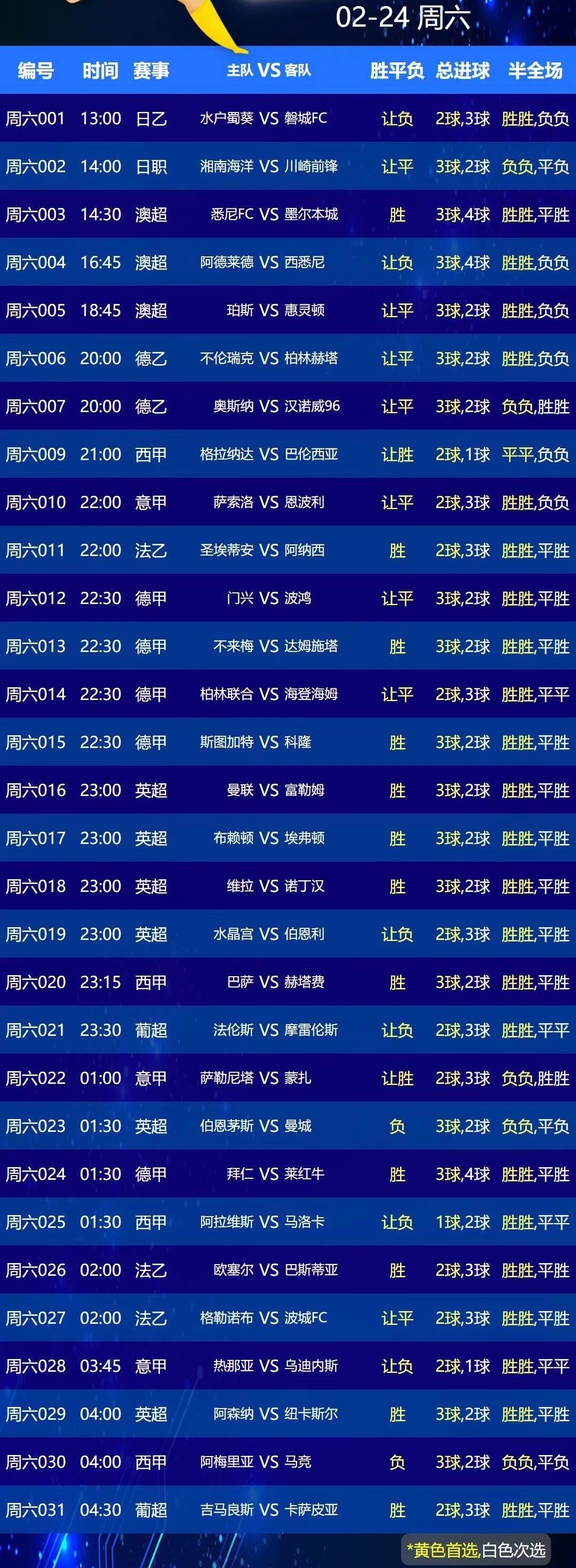
相关文章:

2月24日(周六)比赛前瞻:曼联 VS 富勒姆、拜仁 VS 莱比锡
大家好,博主将持续更新胜负14场前瞻,此处每日赛事间歇更新,胃信号每日更新。 精选赛事:曼联 VS 富勒姆 曼联近期状态显著提升,上一轮联赛客场2-1战胜卢顿,连续7场正赛取得6胜1平的成绩,保持不败…...

React18源码: task任务调度和时间分片
任务队列管理 调度的目的是为了消费任务,接下来就具体分析任务队列是如何管理与实现的 在 Scheduler.js 中,维护了一个 taskQueue, 任务队列管理就是围绕这个 taskQueue 展开 // Tasks are stored on a min heap var taskQueue - []; var timerQueue …...
)
【工具类】阿里域名关联ip(python版)
获取代码如下 # codingutf-8import argparse import json import urllib import logging# 加载 ali 核心 SDK from aliyunsdkcore.client import AcsClient from aliyunsdkalidns.request.v20150109 import (DescribeSubDomainRecordsRequest,AddDomainRecordRequest,UpdateDo…...

STM32自学☞输入捕获测频率和占空比案例
本文是通过PA0口输出PWM波,然后通过PA6口捕获PWM波的频率和占空比,最终在oled屏上显示我们自己设置的频率和占空比。由于和前面的pwm呼吸灯代码有重合部分所以本文中的代码由前者修改而来,对于文件命名不要在意。 pwm_led.c文件 /* 编写步…...
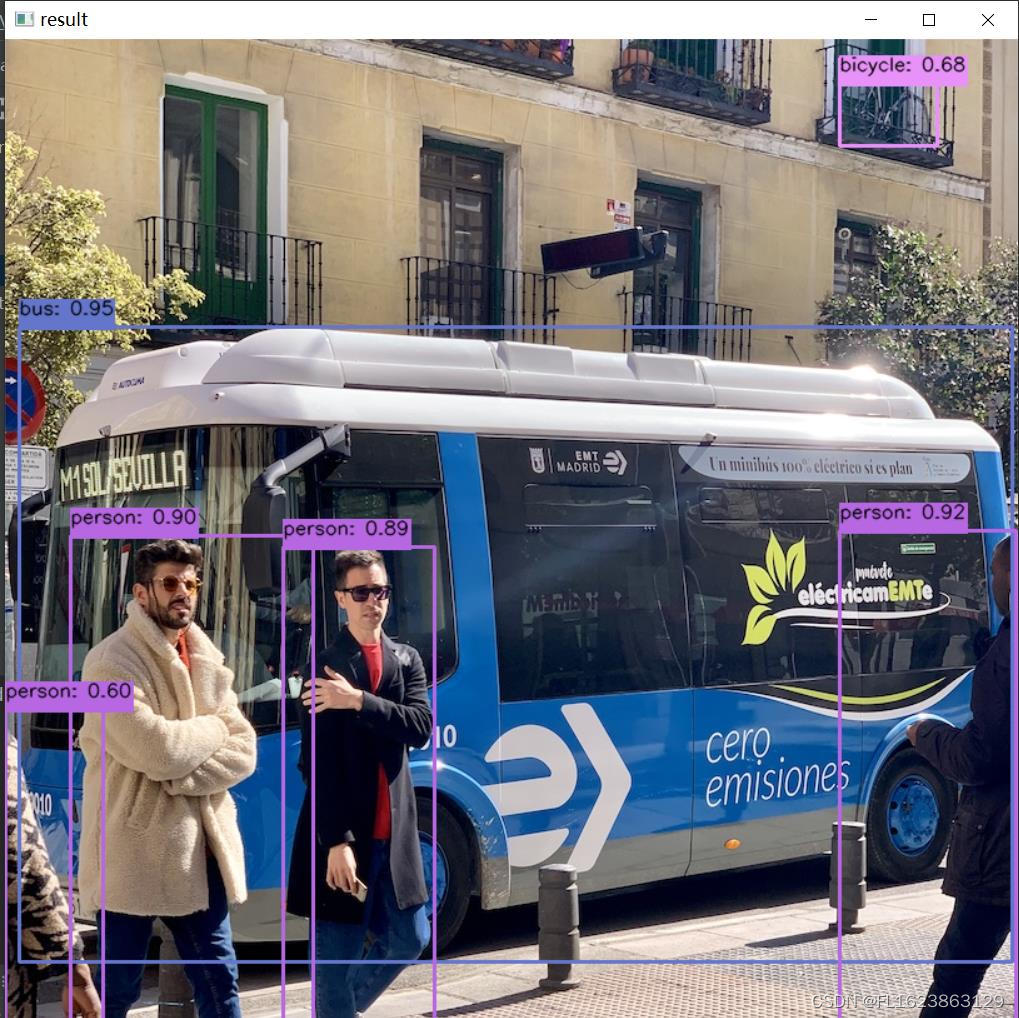
[yolov9]使用python部署yolov9的onnx模型
【框架地址】 https://github.com/WongKinYiu/yolov9 【yolov9简介】 在目标检测领域,YOLOv9 实现了一代更比一代强,利用新架构和方法让传统卷积在参数利用率方面胜过了深度卷积。 继 2023 年 1 月 正式发布一年多以后,YOLOv9 终于来了&a…...

ShellExecute的用法
1、标准用法 ShellExecute函数原型及参数含义如下: function ShellExecute(hWnd: HWND; Operation, FileName, Parameters,Directory: PChar; ShowCmd: Integer): HINST; stdcall; ●hWnd:用于指定父窗口句柄。当函数调用过程出现错误时,它将…...

蓝桥杯:递增三元组
题目 递增三元组(2018年蓝桥杯真题) 题目描述: 给定三个整数数组 A [A1, A2, … AN], B [B1, B2, … BN], C [C1, C2, … CN], 请你统计有多少个三元组(i, j, k) 满足: 1 < i, j, k < N Ai < Bj &…...
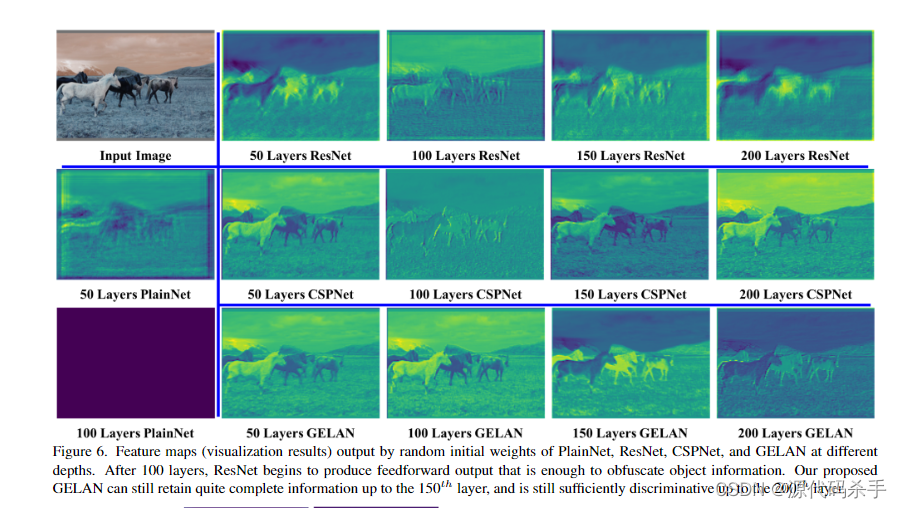
目标检测卷王YOLO卷出新高度:YOLOv9问世
论文摘要:如今的深度学习方法重点关注如何设计最合适的目标函数,使得模型的预测结果能够最接近真实情况。 同时,必须设计一个适当的架构,可以帮助获取足够的信息进行预测。 现有方法忽略了一个事实,即当输入数据经过逐层特征提取和空间变换时,大量信息将会丢失。 本文将深…...
华为---RSTP(二)---RSTP基本配置示例
目录 1. 示例要求 2. 网络拓扑图 3. 配置命令 4. 测试终端连通性 5. RSTP基本配置 5.1 启用STP 5.2 修改生成树协议模式为RSTP 5.3 配置根交换机和次根交换机 5.4 设置边缘端口 6. 指定端口切换为备份端口 7. 测试验证网络 1. 示例要求 为防止网络出现环路…...
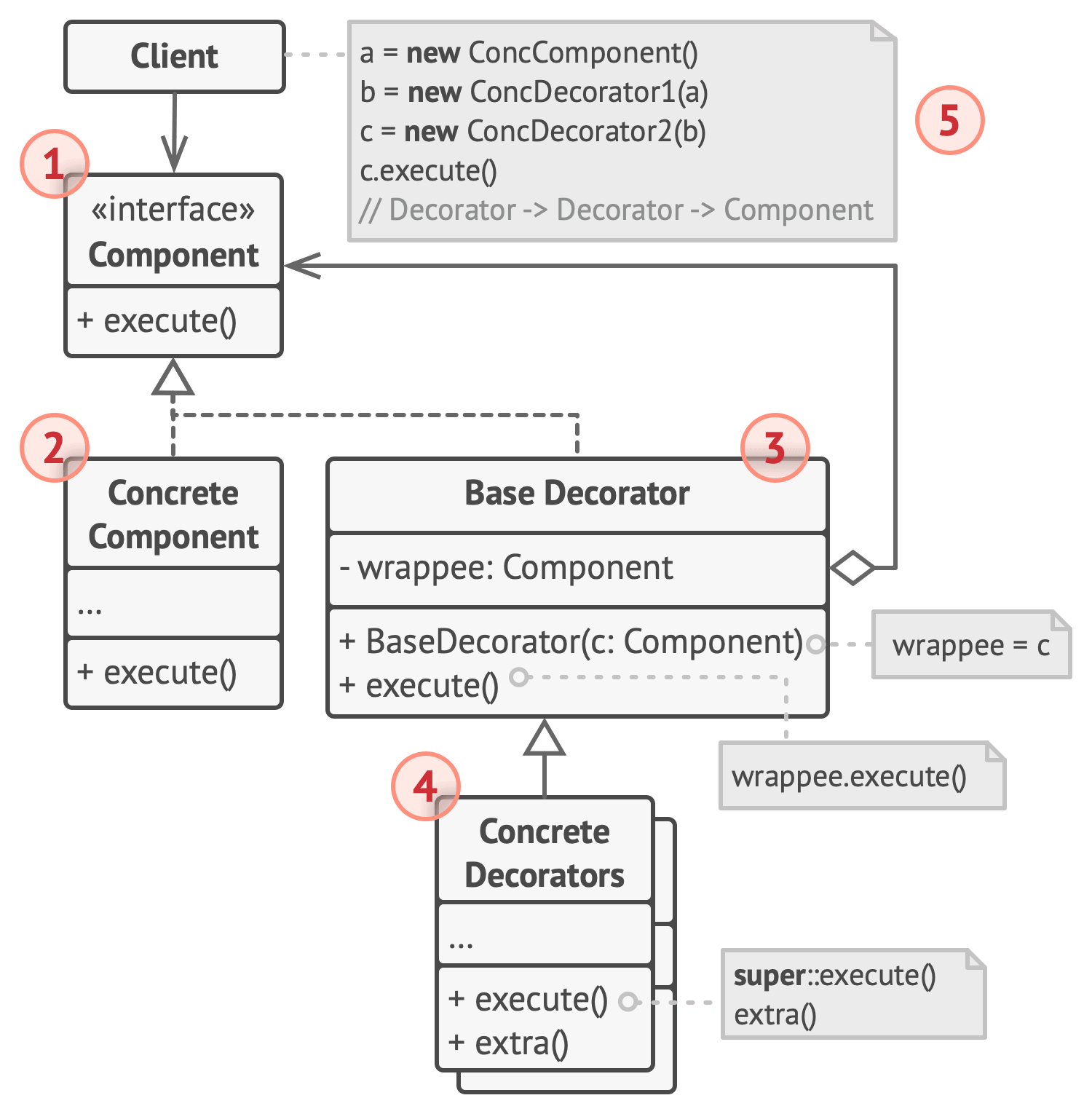
【Python笔记-设计模式】装饰器模式
一、说明 装饰器模式是一种结构型设计模式,旨在动态的给一个对象添加额外的职责。 (一) 解决问题 不改变原有对象结构的情况下,动态地给对象添加新的功能或职责,实现透明地对对象进行功能的扩展。 (二) 使用场景 如果用继承来扩展对象行…...
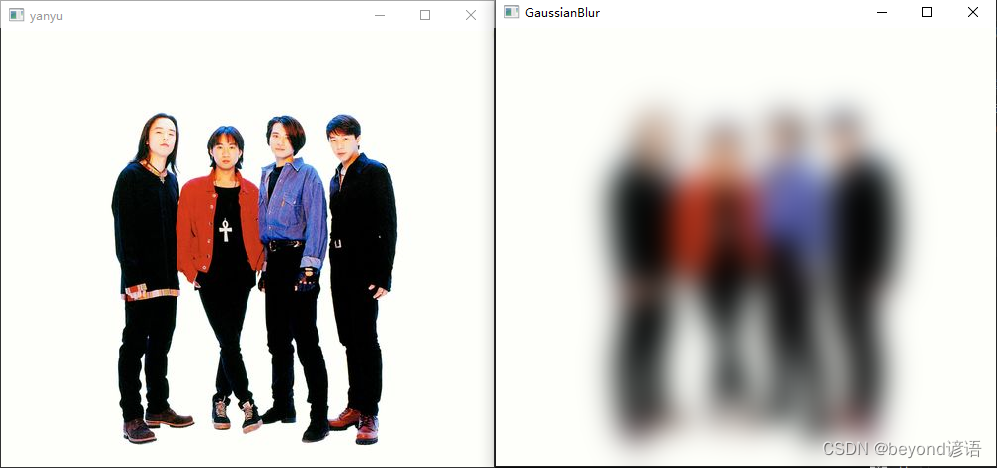
二十八、图像的高斯模糊操作
项目功能实现:对一张图片进行高斯模糊操作 按照之前的博文结构来,这里就不在赘述了 更多的图像模糊操作原理可参考博文:七、模糊操作,里面有详细原理讲解,只不过代码是python写的。 一、头文件 gaussian_blur.h #p…...
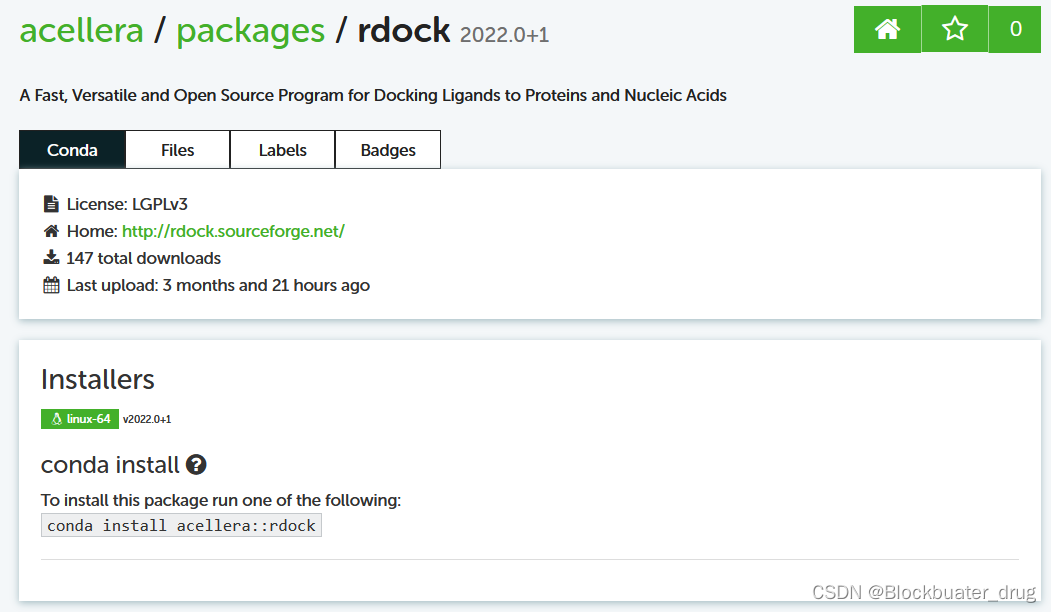
开源分子对接程序rDock的安装及使用流程
欢迎浏览我的CSND博客! Blockbuater_drug …点击进入 前言 本文介绍开源分子对接程序rDock在Linux Ubuntu 22.04系统上的conda安装、编译安装过程及程序使用流程。 一、rDock是什么? rDock来源 rDock是一个快速、多功能的开源对接程序,可用…...
【JavaEE】_tomcat的安装与使用
目录 1. Tomcat简介 2. Tomcat安装 2.1 下载Tomcat并解压缩 2.2 启动Tomcat 2.2.1 Tomcat乱码问题 2.2.2 Tomcat闪退问题 2.3 访问Tomcat欢迎页面 3. 使用Tomcat部署前端代码 3.1 路径匹配 3.2 文件路径访问与网络访问 4. 静态页面与动态页面 5. 基于tomcat的网站后…...

实现一个Windows环境一键启停Oracle的bat脚本
Oracle数据库有许多优点,其中一些最重要的包括: 可靠性和稳定性: Oracle数据库经过长期的发展和测试,被广泛认为是非常可靠和稳定的数据库管理系统。它在大型企业和关键业务环境中被广泛应用,能够处理高负载和大规模的数据。 高性能: Oracle数据库具有优化的查询处理器和…...
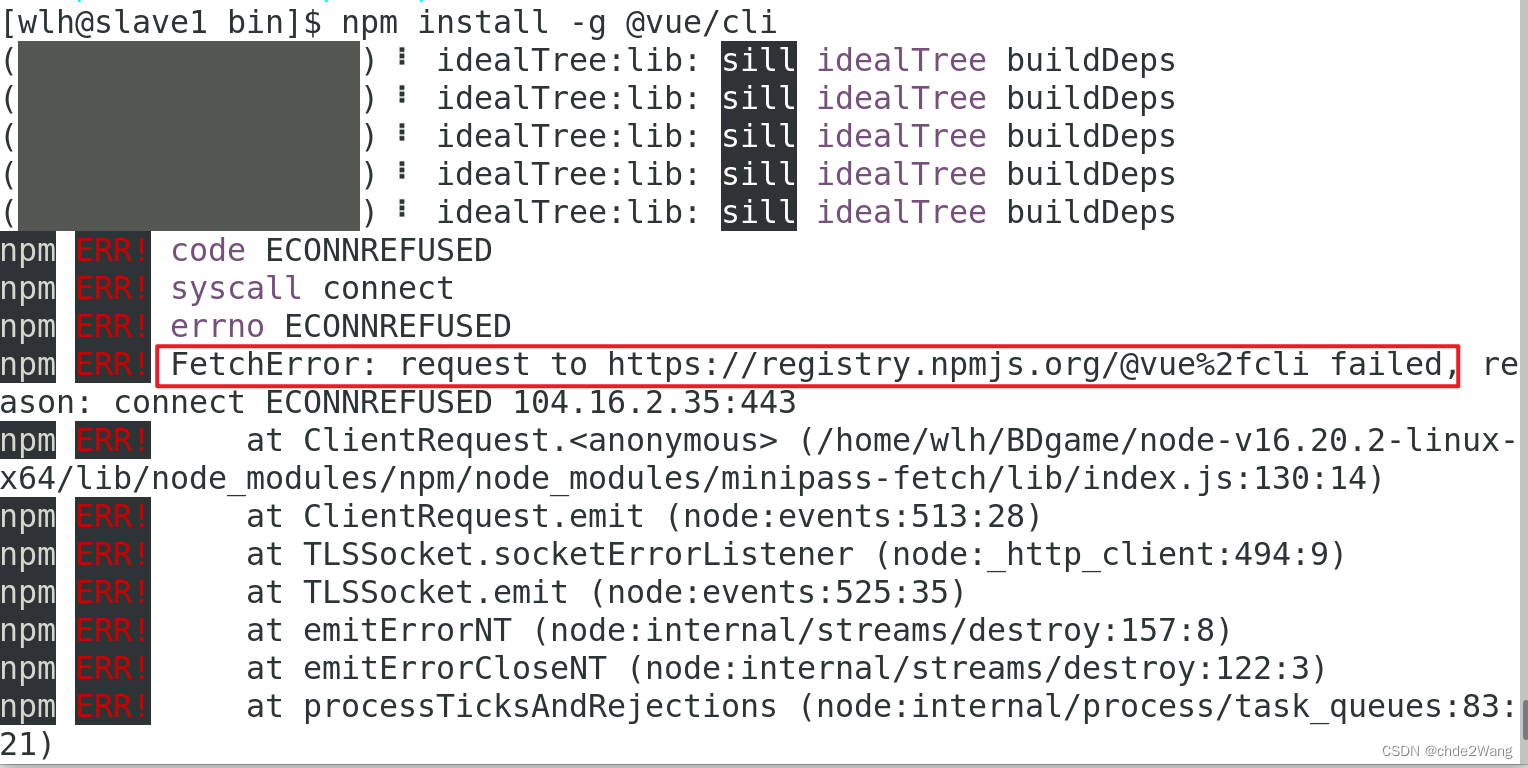
大数据-数据可视化-环境部署vue+echarts+显示案例
文章目录 一、安装node.js1 打开火狐浏览器,下载Node.js2 进行解压3 配置环境变量4 配置生效二、安装vue脚手架1 下载vue脚手架,耐心等待。三、创建vue项目并启动1 创建2 启动四、下载echarts.js与axios.js到本地。五、图表显示demo【以下所有操作均在centos上进行】 一、安…...

spark超大数据批量写入redis
利用spark的分布式优势,一次性批量将7000多万的数据写入到redis中。 # 配置spark接口 import os import findspark from pyspark import SparkConf from pyspark.sql import SparkSession os.environ["JAVA_HOME"] "/usr/local/jdk1.8.0_192"…...

C# Socket的使用
C# 中的 System.Net.Sockets.Socket 类是 .NET Framework 提供的核心类,用于处理网络套接字编程。Socket 类是用于网络编程的基础类,它位于 System.Net.Sockets 命名空间中。 使用 Socket 类,可以创建客户端和服务器应用程序来进行基于TCP、…...

Spring Cloud + Vue前后端分离-第17章 生产打包与发布
源代码在GitHub - 629y/course: Spring Cloud Vue前后端分离-在线课程 Spring Cloud Vue前后端分离-第17章 生产打包与发布 17-1 注册中心配置中心Nacos 注册中心 Nacos 快速开始 | Nacos 本节内容:使用nacos作注册中心配置中心,不用eureka Nacos…...

力扣热题100_普通数组_56_合并区间
文章目录 题目链接解题思路解题代码 题目链接 56. 合并区间 以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区…...
)
Springcloud OpenFeign 的实现(二)
Springcloud OpenFeign 的实现(一) 一、Feign request/response 压缩 您可以考虑为您的外部请求启用请求或响应GZIP压缩。您可以通过启用以下属性之一来完成此操作: feign.compression.request.enabledtrue feign.compression.response.en…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
