线性代数:向量、张量、矩阵和标量
线性代数:向量、张量、矩阵和标量
背景
在线性代数中,向量、张量、矩阵和标量都属于基础概念,特别是最近AI的爆火,向量和张量的概念也越来越普及,本文将介绍下这些基本概念。
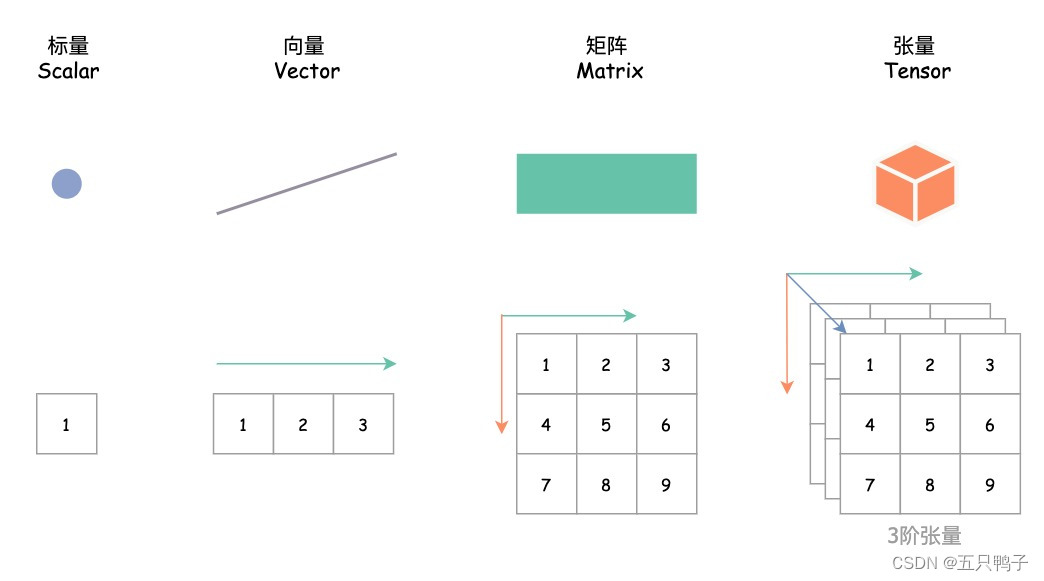
1. 标量(Scalar)
1.1 定义和表示
标量是数学中的一个基本概念,它表示一个单独的实数,没有方向或位置。在数学表示中,我们通常用小写字母表示标量,例如 a 或 x。
1.2 例子
- 温度(32℃)
- 质量(62kg)
- 速度(102km/h)
标量是我们日常生活中常见的量,它们具有大小但没有方向。
在python代码中表示
x = 1# 或者可以表示为0阶张量x = np.array(1)print(x.ndim)
2. 向量(Vector)
2.1 定义和表示
向量是有序的一维数组,其中包含多个标量元素。每个元素都有一个索引,表示其在向量中的位置。在数学表示中,我们通常用小写粗体字母表示向量,如 v。
2.2 例子
- 位移(向东200米)
- 力(向左10牛米)
向量不仅有大小,还有方向,因此它可以表示在空间中的运动或力的作用方向。
2.3 代码和图示
一个二维向量可以表示为
v = [ 1 2 3 ] v = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix} v=[123]
在python代码中表示
v = np.array([1, 2, 3])print(v.ndim) # = 1
3. 矩阵(Matrix)
3.1 定义和表示
矩阵是一个二维数组,其中包含多个标量元素,这些元素按行和列排列。在数学表示中,我们通常用大写字母表示矩阵,如 A。
3.2 例子
- 图像的像素值
- 线性变换
公式和图示
一个 m x n 的矩阵 A 可以表示为:
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} A= a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn
在python代码中例子
m = np.array([[1, 2], [3, 4]])print(m.ndim) # = 2
4. 张量(Tensor)
4.1 定义和表示
在线性代数里面可以简单的将张量理解为一个多维数组,可以包含标量、向量和矩阵。在数学表示中,我们通常用大写粗体字母表示张量,如 T
4.2 例子
- 神经网络中的输入
- 多模态数据的表示,如图片语音视频等
公式和图示
在深度学习中,一个三维张量 T 可以表示为:
T = [ A B C D E F G H I ] \mathbf{T} = \begin{bmatrix} \mathbf{A} & \mathbf{B} & \mathbf{C} \\ \mathbf{D} & \mathbf{E} & \mathbf{F} \\ \mathbf{G} & \mathbf{H} & \mathbf{I} \end{bmatrix} T= ADGBEHCFI
这里A、B、C、D等可以是标量、向量或矩阵。
之间的关系
- 标量是零阶张量,向量是一阶张量,矩阵是二阶张量。
- 张量的阶数表示它包含的维度数量,不止是3阶张量,张量可以是无数阶。
- 从这种角度来看,万物皆张量
相关文章:

线性代数:向量、张量、矩阵和标量
线性代数:向量、张量、矩阵和标量 背景 在线性代数中,向量、张量、矩阵和标量都属于基础概念,特别是最近AI的爆火,向量和张量的概念也越来越普及,本文将介绍下这些基本概念。 1. 标量(Scalar࿰…...

WordPres Bricks Builder 前台RCE漏洞
免责声明:文章来源互联网收集整理,请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失,均由使用者本人负责,所产生的一切不良后果与文章作者无关。该…...
渗透测试—信息收集
渗透测试—信息收集 1. 收集域名信息1.1. 域名注册信息1.2. SEO信息收集1.3. 子域名收集1.3.1. 在线子域名收集1.3.2. 子域名收集工具 1.4. 域名备案信息1.5. ICP备案号查询1.6. SSL证书查询 2. 收集真实IP2.1. 超级ping2.2. Ping2.3. CDN绕过 3. 收集旁站或C段IP3.1. 旁站或C段…...
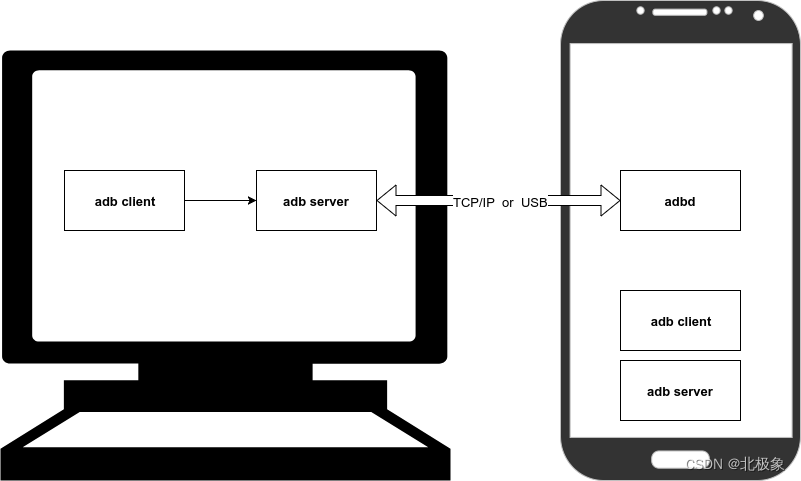
安卓adb调试备忘录
由于 MAC 的 USB 口全被占用着,采用无线连接刚方便,记录一下,以防忘记~ ADB原理 adb devices -l ## 列出连接的设备adb tcpip [端口号] adb tcpip 6666 # 将当前已连接USB上的Mobile端切换为TCP/IP模式,以6666端口进行监听. adb…...
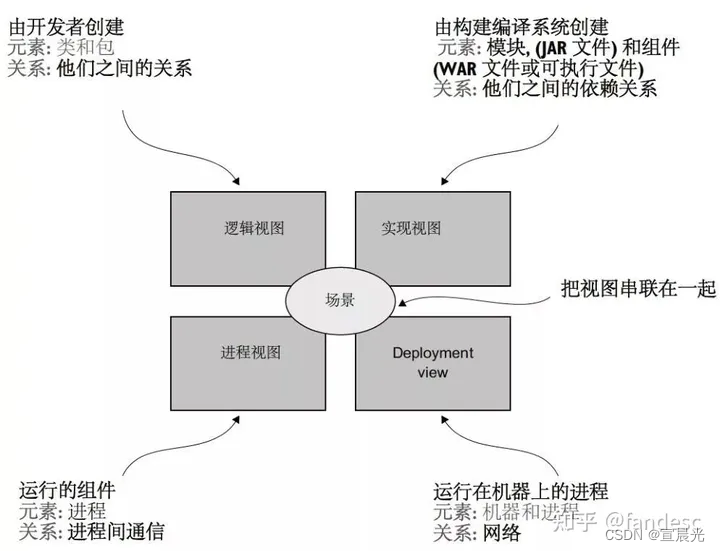
【软件架构】01-架构的概述
1、定义 软件架构就是软件的顶层结构 RUP(统一过程开发)4 1 视图 1)逻辑视图: 描述系统的功能、组件和它们之间的关系。它主要关注系统的静态结构,包括类、接口、包、模块等,并用于表示系统的组织结构…...

Vue 图片轮播第三方库 介绍
Vue图片轮播是一种在网页上以自动或手动方式展示图片的组件,常用于产品展示、网站banner等场景。有许多第三方库可以帮助Vue开发者轻松实现图片轮播功能。以下是一些流行的Vue图片轮播第三方库的介绍: 1. Vue-awesome-swiper - **简介**:V…...

设置主从复制时发生报错Could not find first log file name in binary log index file‘;解决方案
如图所示,slave_io_runnind:no,slave_sql_running:yes 此时,主从配置错误,我们可以查看Last_IO_Error:来查看报错信息 此时,我们需要停止从服务器的主从服务, mysql> stop slave; Query OK, 0 rows affected, 1 w…...

React Context的使用方法
背景:在某些场景下,你想在整个组件树中传递数据,但却不想手动地在每一层传递属性,你可以直接在React中使用强大的contextAPI 解决上述问题 在一个典型的React 中,数据通过Props属性自下而上(由父及子&…...

ElasticSearch索引数据备份与恢复
索引数据备份 在磁盘创建备份目录并授权 # 创建备份目录 /home/esbackup # 授权 chmod 777 /home/esbackup修改配置文件elasticsearch.yml echo path.repo: ["/home/esbackup"] >> /etc/elasticsearch/elasticsearch.yml重启elasticsearch(我是docker创建的…...

kubernetes日志收集 fluent-operator 动态索引名的实现
文章目录 按照服务名区分索引名1.修改fluent-operator,让其支持logstash_prefix_key2.让它能获取app name作为服务名3. 拼接索引名4. 应用变更 发自个人博客: https://uublog.com/article/20230510/kubernetes-fluent-operator-dynamic-index-name/ 日志…...

pip换源
windows环境下: 比如windows账号是 admin 那么建立 admin主目录下的 pip子目录,在此pip子目录下建立pip的配置文件:pip.ini c:\users\admin\pip\pip.ini # coding: GBK [global] index-url https://pypi.tuna.tsinghua.edu.cn/simple [ins…...

7.(数据结构)堆
7.1 相关概念 堆(Heap)在计算机科学中是一种特殊的数据结构,它通常被实现为一个可以看作完全二叉树的数组对象。以下是一些关于堆的基本概念: 数据结构: 堆是一个优先队列的抽象数据类型实现,通过完全二叉树…...

AWS Elastic Beanstalk通过应用负载均衡配置https
接上一篇,今天说说怎么通过AWS Elastic Beanstalk提供的应用负载均衡配置https。 首先创建应用和环境,这里应用可以使用上一篇文章中使用的demo应用(只需要package.json和app.js文件) 创建环境的时候,确认下面两个参…...

AC自动机:文本搜索的加速器
在数字化时代,文本数据的海洋浩瀚无垠。我们经常需要在这些数据中迅速找到特定的信息,比如在日志文件中查找异常、在海量文本中检索关键词,或是在编译代码时识别语法结构。这时候,AC自动机(Aho-Corasick自动机…...

备战蓝桥杯---基础算法刷题1
最近在忙学校官网上的题,就借此记录分享一下有价值的题: 1.注意枚举角度 如果我们就对于不同的k常规的枚举,复杂度直接炸了。 于是我们考虑换一个角度,我们不妨从1开始枚举因子,我们记录下他的倍数的个数sum个&#…...

探索 Flutter 中的动画:使用 flutter_animate
在移动应用开发中,动画是提升用户体验和吸引用户注意力的关键要素之一。Flutter 作为一种跨平台的移动应用开发框架,提供了丰富而灵活的动画支持。其中,flutter_animate 是一个强大的库,它为 Flutter 开发者提供了简单易用的方式来…...

装机容量对光伏发电量的影响有多大?如何通过装机容量计算发电量?
光伏行业得益于全球对环保和可持续发展的重视,得到了快速的发展。众所周知,光伏电站的收益受发电量的影响,发电量越大收益越高,但发电量其实受装机容量的影响。 一、装机容量对发电量的影响 光伏发电的核心就是发电板࿰…...

软考37-上午题-【数据库】-数据模型、数据库的三级模式和二级映像
一、考情简介 上午题:6分——6道选择题 下午题:15分——一道分析题 E-R图、关系模式:下午考试必考!!!(编制也要考!) 二、数据模型 数据模型是对现实世界数据特征的抽象…...
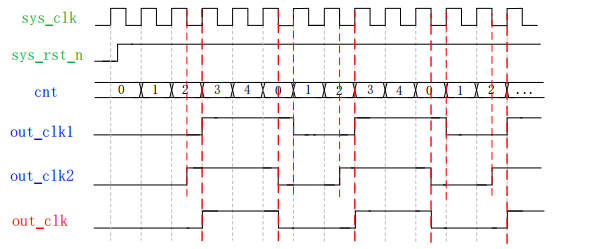
06 分频器设计
分频器简介 实现分频一般有两种方法,一种方法是直接使用 PLL 进行分频,比如在 FPGA 或者 ASIC 设计中,都可以直接使用 PLL 进行分频。但是这种分频有时候受限于 PLL 本身的特性,无法得到频率很低的时钟信号,比如输入 …...

力扣hot100题解(python版7-9题)
7、接雨水 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...

32位寻址与64位寻址
32位寻址与64位寻址 32位寻址是什么? 32位寻址是指计算机的CPU、内存或总线系统使用32位二进制数来标识和访问内存中的存储单元(地址),其核心含义与能力如下: 1. 核心定义 地址位宽:CPU或内存控制器用32位…...

嵌入式面试常问问题
以下内容面向嵌入式/系统方向的初学者与面试备考者,全面梳理了以下几大板块,并在每个板块末尾列出常见的面试问答思路,帮助你既能夯实基础,又能应对面试挑战。 一、TCP/IP 协议 1.1 TCP/IP 五层模型概述 链路层(Link Layer) 包括网卡驱动、以太网、Wi‑Fi、PPP 等。负责…...
