7.(数据结构)堆
7.1 相关概念
堆(Heap)在计算机科学中是一种特殊的数据结构,它通常被实现为一个可以看作完全二叉树的数组对象。以下是一些关于堆的基本概念:
数据结构:
堆是一个优先队列的抽象数据类型实现,通过完全二叉树的逻辑结构来组织元素。
完全二叉树意味着除了最后一层外,每一层都被完全填满,并且最后一层的所有节点都尽可能地集中在左边。
物理存储:堆用一维数组顺序存储,从索引0开始,每个节点的父节点和子节点之间的关系可以通过简单的算术运算确定。
堆的特性:堆序性质:对于任意节点i,其值(或关键字)满足与它的子节点的关系——在最大堆(大根堆)中,节点i的值大于或等于其两个子节点的值;在最小堆(小根堆)中,节点i的值小于或等于其两个子节点的值。
结构性:堆始终保持完全二叉树的状态,这意味着即使有节点删除或插入,堆也要经过调整以保持堆序性质。
操作:插入:新元素添加到堆中时,需要自下而上调整堆,以确保新的元素不会破坏堆的性质。
删除:通常从堆顶(根节点)删除元素(即最大堆中的最大元素或最小堆中的最小元素),然后将堆尾元素移动到堆顶,再自上而下调整堆。
查找:堆常用于快速找到最大或最小元素,但查找特定值的时间复杂度通常不优于线性时间,因为堆本身不具备随机访问的能力。
应用:堆常用于解决各种问题,如优先级队列、事件调度、图算法中的最短路径计算(Dijkstra算法)、求解Top K问题等。
分类:最常见的堆是二叉堆,包括大根堆和小根堆。
还有其他类型的堆,比如斐波那契堆,提供更高效的合并操作以及其他优化特性。
建堆算法:
1. Dijkstra算法:是一个使用优先队列(可以基于堆实现)的经典例子。在Dijkstra算法中,每次都会从未确定最短路径且当前距离已知最小的顶点开始,更新与其相邻顶点的距离。为了高效地找到下一个待处理的顶点(即当前已知最短路径的顶点),会用到一个能够根据顶点距离值进行快速插入和删除的优先队列,堆就是实现这种功能的理想数据结构之一。
2. 堆下沉”(Heap Sink),“堆下滤”(Heap Percolate Down):从根节点(非叶子节点中最高层的一个)开始。 检查该节点与其两个子节点的关系:在最大堆中,如果当前节点的值小于其任意一个子节点的值;在最小堆中,如果当前节点的值大于其任意一个子节点的值。 如果违反了堆的性质,则交换当前节点与其较大(对于最大堆)或较小(对于最小堆)子节点的值,并将当前节点移动到新位置(即原来子节点的位置)。 重复上述步骤,但这次以交换后的子节点作为新的当前节点,继续下潜至当前节点没有子节点(即成为叶子节点),或者当前节点及其子节点均满足堆的性质为止。
时间复杂度:
相关文章:

7.(数据结构)堆
7.1 相关概念 堆(Heap)在计算机科学中是一种特殊的数据结构,它通常被实现为一个可以看作完全二叉树的数组对象。以下是一些关于堆的基本概念: 数据结构: 堆是一个优先队列的抽象数据类型实现,通过完全二叉树…...

AWS Elastic Beanstalk通过应用负载均衡配置https
接上一篇,今天说说怎么通过AWS Elastic Beanstalk提供的应用负载均衡配置https。 首先创建应用和环境,这里应用可以使用上一篇文章中使用的demo应用(只需要package.json和app.js文件) 创建环境的时候,确认下面两个参…...

AC自动机:文本搜索的加速器
在数字化时代,文本数据的海洋浩瀚无垠。我们经常需要在这些数据中迅速找到特定的信息,比如在日志文件中查找异常、在海量文本中检索关键词,或是在编译代码时识别语法结构。这时候,AC自动机(Aho-Corasick自动机…...

备战蓝桥杯---基础算法刷题1
最近在忙学校官网上的题,就借此记录分享一下有价值的题: 1.注意枚举角度 如果我们就对于不同的k常规的枚举,复杂度直接炸了。 于是我们考虑换一个角度,我们不妨从1开始枚举因子,我们记录下他的倍数的个数sum个&#…...

探索 Flutter 中的动画:使用 flutter_animate
在移动应用开发中,动画是提升用户体验和吸引用户注意力的关键要素之一。Flutter 作为一种跨平台的移动应用开发框架,提供了丰富而灵活的动画支持。其中,flutter_animate 是一个强大的库,它为 Flutter 开发者提供了简单易用的方式来…...

装机容量对光伏发电量的影响有多大?如何通过装机容量计算发电量?
光伏行业得益于全球对环保和可持续发展的重视,得到了快速的发展。众所周知,光伏电站的收益受发电量的影响,发电量越大收益越高,但发电量其实受装机容量的影响。 一、装机容量对发电量的影响 光伏发电的核心就是发电板࿰…...

软考37-上午题-【数据库】-数据模型、数据库的三级模式和二级映像
一、考情简介 上午题:6分——6道选择题 下午题:15分——一道分析题 E-R图、关系模式:下午考试必考!!!(编制也要考!) 二、数据模型 数据模型是对现实世界数据特征的抽象…...
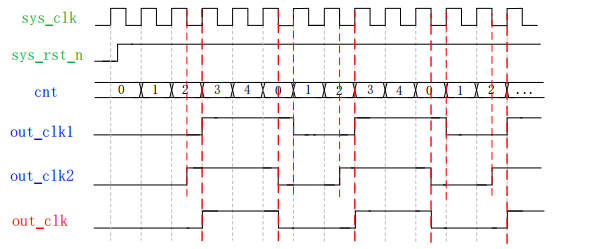
06 分频器设计
分频器简介 实现分频一般有两种方法,一种方法是直接使用 PLL 进行分频,比如在 FPGA 或者 ASIC 设计中,都可以直接使用 PLL 进行分频。但是这种分频有时候受限于 PLL 本身的特性,无法得到频率很低的时钟信号,比如输入 …...

力扣hot100题解(python版7-9题)
7、接雨水 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,…...
 迭代器 与 生成器)
ECMAScript 6+ 新特性 ( 四 ) 迭代器 与 生成器
2.14.迭代器 2.14.1.for…of for...of 是 JavaScript ES6 引入的一种新的循环结构,,用于遍历可迭代对象(Iterable objects)的每个元素。 它可以自动调用目标对象的迭代器接口,并按顺序逐个访问集合中的每个值。 它…...

【MySQL】事务的一致性究竟怎么理解?
众所周知,事务有四大特性:原子性、一致性、隔离性、持久性,除了一致性,其他三类特性都很好理解。而关于一致性的解释有点让人头疼,我查了很多文章,大多类似:事务的执行必须使数据库处于一致状态…...

证件照(兼容H5,APP,小程序)
证件照由uniappuyui开发完成,并同时兼容H5、App、微信小程序、支付宝小程序,其他端暂未测试。 先看部分效果图吧具体可以下方复制链接体验demo 首页代码 <template><view class""><view class"uy-m-x-30 uy-m-b-20"…...

pytorch-textregression,中文文本回归实践,支持多值输出
pytorch-textregression,中文文本回归实践,支持多值输出 pytorch-textregression是一个以pytorch和transformers为基础,专注于中文文本回归的轻量级自然语言处理工具,支持多值回归等。 目录 数据使用方式paper参考 项目地址 py…...

go语言学而思【持续更新】
问题:在Go语言中nil是什么意思? 答:在Go语言中,nil是一个预声明的标识符,用于表示某些类型的零值。它可以被用作以下类型的零值: 指针(Pointer)切片(Slice)…...
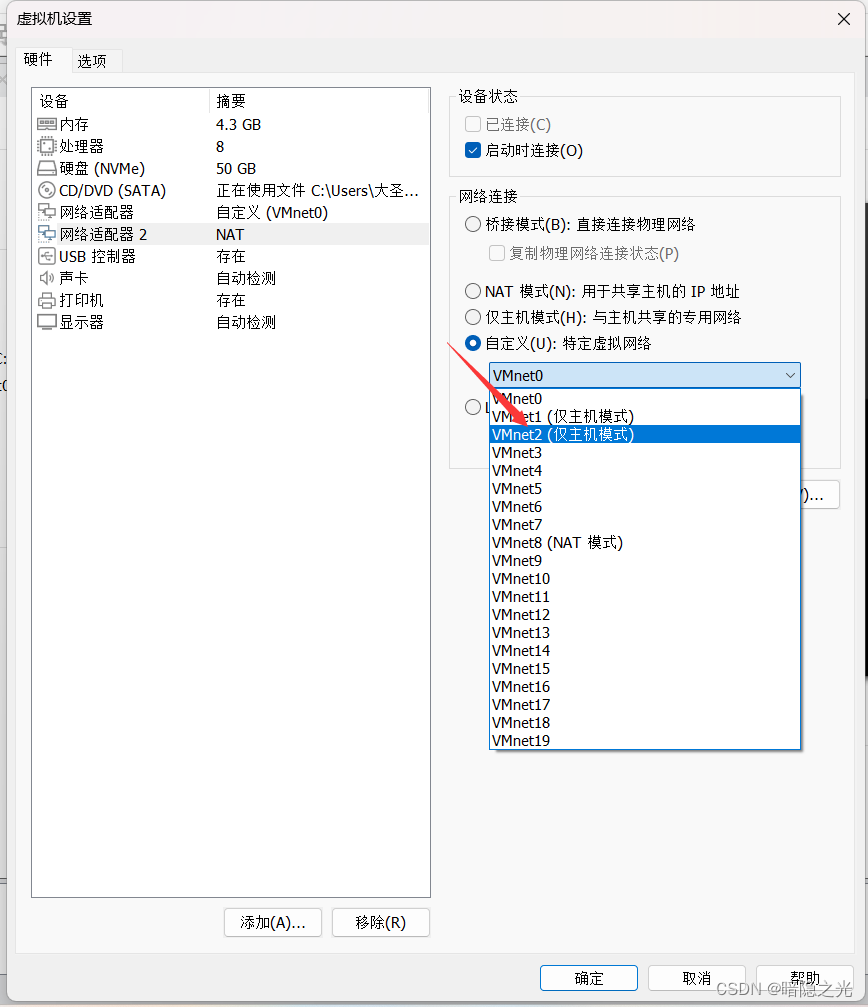
LVS-NAT之VMNET环境搭建
目录 搭建拓扑图 搭建规划 VMNET0 搭建 VMNET2 搭建 LVS端增加网卡 搭建拓扑图: 搭建规划: CLIENT(servera): VMNET0 LVS(serverb): VMNET0 VMNET2 WEB1(serverd): VMNET2 WEB2(servere): VMNET2 VMNE…...
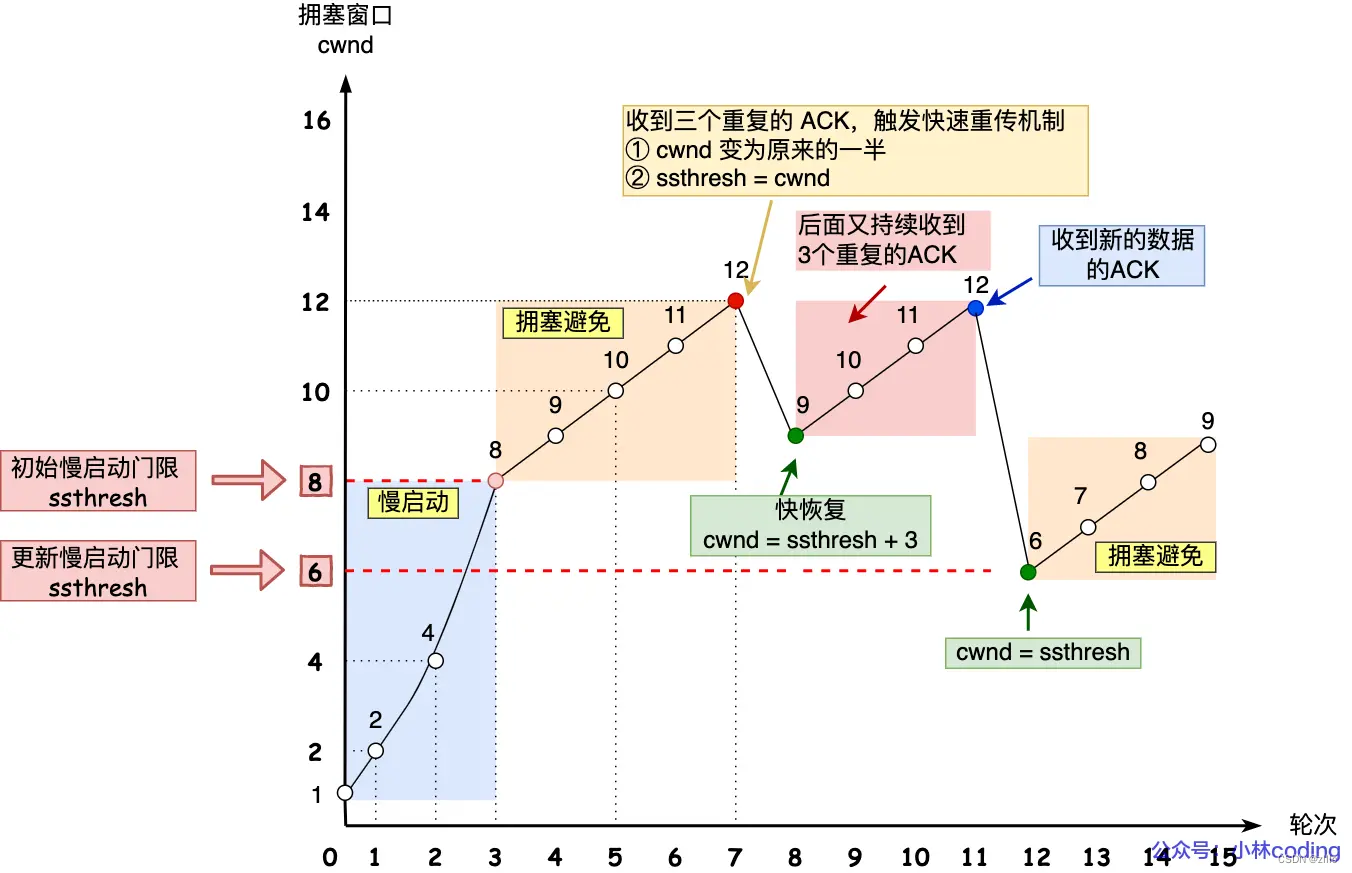
[TCP] TCP/IP 基础知识词典(2)
我想统计一下,TCP/IP 尤其是TCP协议,能搜到的常见的问题,整理起来,关键词添加在目录中,便于以后查阅。 目前预计整理共3篇: [TCP] TCP/IP 基础知识问答 :基础知识 [TCP] TCP/IP 基础知识问答&…...

【牛牛送书 | 第四期】《高效使用Redis:一书学透数据存储与高可用集群》带你快速学习使用Redis
前言: 当今互联网技术日新月异,随着数据量的爆炸式增长,如何高效地存储和管理数据成为了每个公司都必须面对的挑战。与此同时,用户对于应用程序的响应速度和稳定性要求也越来越高。在这个背景下,Redis 作为一个…...
Threejs 实现3D影像地图,Json地图,地图下钻
1.使用threejs实现3D影像地图效果,整体效果看起来还可以,底层抽象了基类,实现了通用,对任意省份,城市都可以只替换数据,即可轻松实现效果。 效果如下: 链接https://www.bilibili.com/video/BV1…...
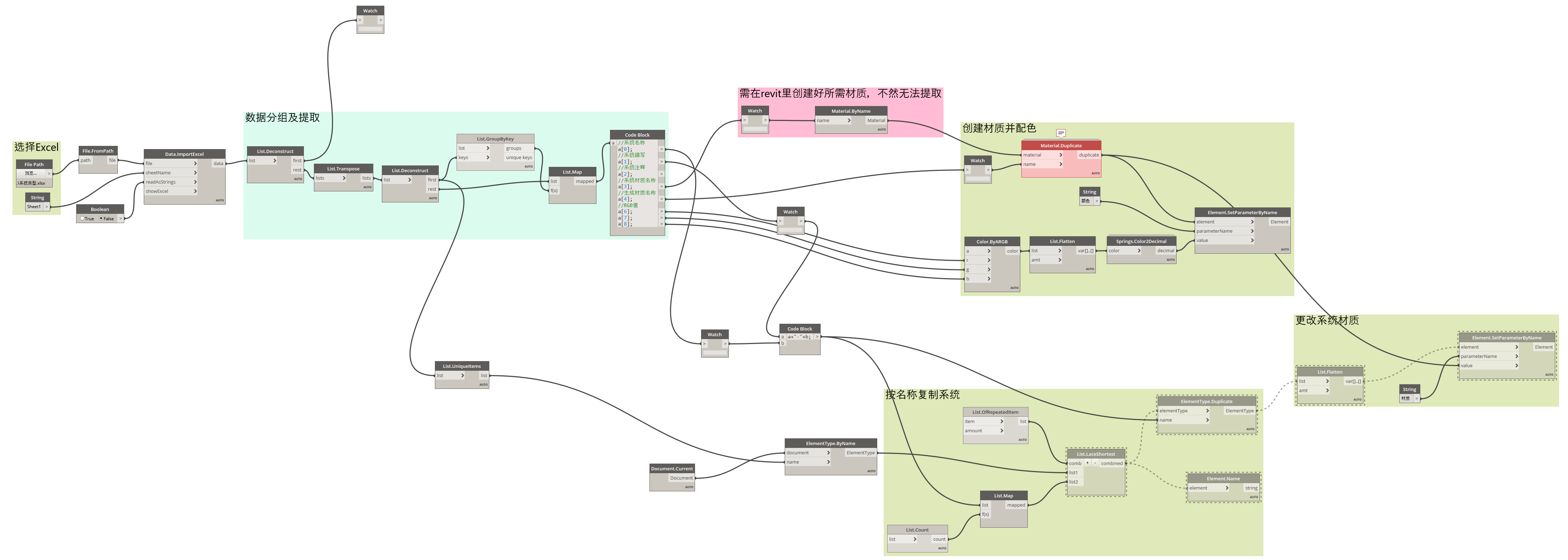
根据Excel创建管道系统及材质
之前看过程鑫老师的文章,介绍过根据Excel数据创建管道系统,但是有小伙伴问过我,照着他这个做,没成功,于是呢,我就想试下,结果发现也没成功。 然后我逐个节点过了一遍,发现可能是因为…...

第八篇【传奇开心果系列】python的文本和语音相互转换库技术点案例示例:Google Text-to-Speech虚拟现实(VR)沉浸式体验经典案例
传奇开心果博文系列 系列博文目录python的文本和语音相互转换库技术点案例示例系列 博文目录前言一、雏形示例代码二、扩展思路介绍三、虚拟导游示例代码四、交互式学习示例代码五、虚拟角色对话示例代码六、辅助用户界面示例代码七、实时语音交互示例代码八、多语言支持示例代…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...
