LeetCode 2583.二叉树中的第 K 大层和:层序遍历 + 排序
【LetMeFly】2583.二叉树中的第 K 大层和:层序遍历 + 排序
力扣题目链接:https://leetcode.cn/problems/kth-largest-sum-in-a-binary-tree/
给你一棵二叉树的根节点 root 和一个正整数 k 。
树中的 层和 是指 同一层 上节点值的总和。
返回树中第 k 大的层和(不一定不同)。如果树少于 k 层,则返回 -1 。
注意,如果两个节点与根节点的距离相同,则认为它们在同一层。
示例 1:
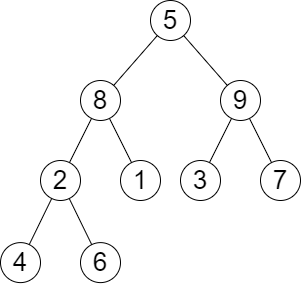
输入:root = [5,8,9,2,1,3,7,4,6], k = 2 输出:13 解释:树中每一层的层和分别是: - Level 1: 5 - Level 2: 8 + 9 = 17 - Level 3: 2 + 1 + 3 + 7 = 13 - Level 4: 4 + 6 = 10 第 2 大的层和等于 13 。
示例 2:

输入:root = [1,2,null,3], k = 1 输出:3 解释:最大的层和是 3 。
提示:
- 树中的节点数为
n 2 <= n <= 1051 <= Node.val <= 1061 <= k <= n
方法一:层序遍历 + 排序
如果已经掌握了二叉树的层序遍历,那么这道题将会如鱼得水。
我们依然进行层序遍历,在层序遍历的过程中,计算每一层的节点值之和,并加入到一个数组中。
遍历结束后,对数组进行排序,返回第k大值或-1即可。
- 时间复杂度 O ( N 1 + N 2 log N 2 ) O(N1 + N2\log N2) O(N1+N2logN2),其中 N 1 N1 N1是二叉树节点个数, N 2 N2 N2是二叉树深度
- 空间复杂度 O ( N 3 + N 2 ) O(N3 + N2) O(N3+N2),其中 N 3 N3 N3是最多一层的节点个数
时空复杂度也可以将全部的 N N N都视为二叉树节点个数。
AC代码
C++
typedef long long ll;
class Solution {
public:ll kthLargestLevelSum(TreeNode* root, int k) {vector<ll> values;queue<TreeNode*> q;q.push(root);while (q.size()) {ll cnt = 0;for (int _ = q.size(); _ > 0; _--) {TreeNode* thisNode = q.front();q.pop();cnt += thisNode->val;if (thisNode->left) {q.push(thisNode->left);}if (thisNode->right) {q.push(thisNode->right);}}values.push_back(cnt);}sort(values.begin(), values.end());return k > values.size() ? -1 : values[values.size() - k];}
};
Python
注意本题数据级别是 1 0 5 10^5 105,不能使用数组切片模拟队列的方式。
# # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = rightclass Solution:def kthLargestLevelSum(self, root: TreeNode, k: int) -> int:values = []q = [root]while q:cnt = 0thisLayer = qq = []for thisNode in thisLayer:cnt += thisNode.valif thisNode.left:q.append(thisNode.left)if thisNode.right:q.append(thisNode.right)values.append(cnt)values.sort()return values[len(values) - k] if len(values) >= k else -1
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/136252010
相关文章:

LeetCode 2583.二叉树中的第 K 大层和:层序遍历 + 排序
【LetMeFly】2583.二叉树中的第 K 大层和:层序遍历 排序 力扣题目链接:https://leetcode.cn/problems/kth-largest-sum-in-a-binary-tree/ 给你一棵二叉树的根节点 root 和一个正整数 k 。 树中的 层和 是指 同一层 上节点值的总和。 返回树中第 k …...

element ui 安装 简易过程 已解决
我之所以将Element归类为Vue.js,其主要原因是Element是(饿了么团队)基于MVVM框架Vue开源出来的一套前端ui组件。我最爱的就是它的布局容器!!! 下面进入正题: 1、Element的安装 首先你需要创建…...

websoket
WebSockets 是一种先进的技术。它可以在用户的浏览器和服务器之间打开交互式通信会话。你可以向服务器发送消息并接收事件驱动的响应,而无需通过轮询服务器的方式以获得响应,比较典型的应用场景就是即时通讯(聊天)系统。 <!DOC…...

案例:微服务从Java/SpringBoot迁移到Golan
基于 Java 的微服务,特别是那些使用 Spring Boot 的微服务,长期以来因其强大的功能和广泛的社区支持而闻名。Spring Boot 的约定优于配置方法简化了微服务的部署和开发,提供了大量开箱即用的功能,例如自动配置、独立功能和简单的依…...

小波变换模拟
小波变换是一种信号处理技术,通过在时间-频率域中使用基于小波的函数进行信号分析。小波变换在处理非平稳信号和图像时特别有用,可以将信号分解为不同频率的成分。它在数据压缩、去噪、特征提取等领域有广泛应用。 MATLAB中提供了用于二维离散小波变换的…...

cv::Mat图像操作
图像读写 //include header #include <opencv2/imgcodecs.hpp>/** Currently, the following file formats are supported: Windows bitmaps - *.bmp, *.dib (always supported) JPEG files - *.jpeg, *.jpg, *.jpe (see the Note section) JPEG 2000 files - *.jp2 (s…...

【机器学习基础】一元线性回归(适合初学者的保姆级文章)
🚀个人主页:为梦而生~ 关注我一起学习吧! 💡专栏:机器学习 欢迎订阅!后面的内容会越来越有意思~ 💡往期推荐: 【机器学习基础】机器学习入门(1) 【机器学习基…...

2024年软件测试岗位-面试
第一部分: 1、自我介绍:简历写到的快速描述,学校、学历、工作经验等(注意:不要过度优化简历,你不写别人可能会问,但你写了别人一定会问!) 第二部分: 1、功能测…...

【坑】Spring Boot整合MyBatis,一级缓存失效
一、Spring Boot整合MyBatis,一级缓存失效 1.1、概述 MyBatis一级缓存的作用域是同一个SqlSession,在同一个SqlSession中执行两次相同的查询,第一次执行完毕后,Mybatis会将查询到的数据缓存起来(缓存到内存中…...
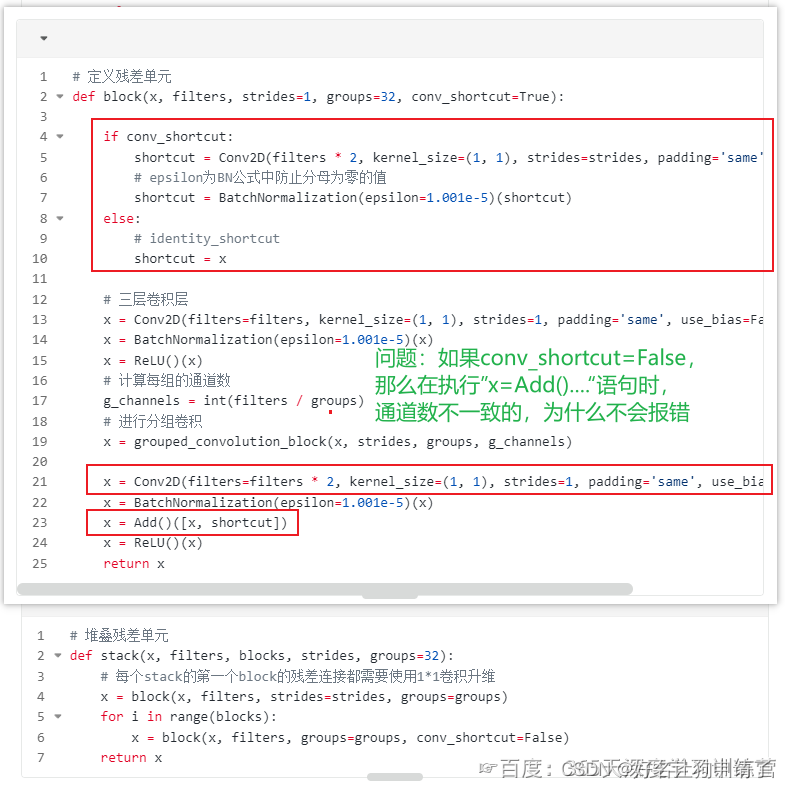
J7 - 对于ResNeXt-50算法的思考
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 | 接辅导、项目定制 J6周有一段代码如下 思考过程 首先看到这个问题的描述,想到的是可能使用了向量操作的广播机制然后就想想办法验证一下&…...
基础篇)
R3F(React Three Fiber)基础篇
之前一直在做ThreeJS方向,整理了两篇R3F(React Three Fiber)的文档,这是基础篇,如果您的业务场景需要使用R3F,您又对R3F不太了解,或者不想使用R3F全英文文档,您可以参考一下这篇&…...

torch\tensorflow在大语言模型LLM中的作用
文章目录 torch\tensorflow在大语言模型LLM中的作用 torch\tensorflow在大语言模型LLM中的作用 在大型语言模型(LLM)中,PyTorch和TensorFlow这两个深度学习框架起着至关重要的作用。它们为构建、训练和部署LLM提供了必要的工具和基础设施。 …...
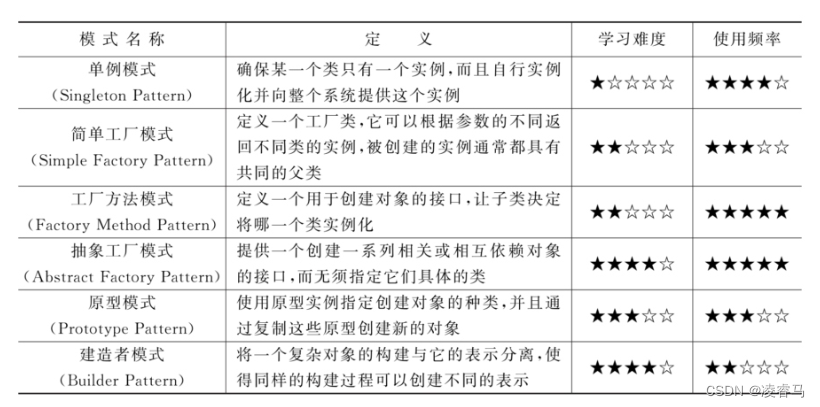
设计模式-创建型模式-单例模式
0 引言 创建型模式(Creational Pattern)关注对象的创建过程,是一类最常用的设计模式,每个创建型模式都通过采用不同的解决方案来回答3个问题:创建什么(What),由谁创建(W…...
备战蓝桥杯—— 双指针技巧巧答链表1
对于单链表相关的问题,双指针技巧是一种非常广泛且有效的解决方法。以下是一些常见问题以及使用双指针技巧解决: 合并两个有序链表: 使用两个指针分别指向两个链表的头部,逐一比较节点的值,将较小的节点链接到结果链表…...

微信小程序返回上一级页面并自动刷新数据
文章目录 前言一、获取小程序栈二、生命周期触发总结 前言 界面由A到B,在由B返回A,触发刷新动作 一、获取小程序栈 界面A代码 shuaxin(){//此处可进行接口请求从而实现更新数据的效果console.log("刷新本页面数据啦")},界面B代码 // 返回触…...

Spring⼯⼚创建复杂对象
文章目录 5. Spring⼯⼚创建复杂对象5.1 什么是复杂对象5.2 Spring⼯⼚创建复杂对象的3种⽅式5.2.1 FactoryBean 接口5.2.2 实例⼯⼚5.2.3 静态工厂 5.3 Spring 工厂的总结 6. 控制Spring⼯⼚创建对象的次数6.1 如何控制简单对象的创建次数6.2 如何控制复杂对象的创建次数6.3 为…...

Top-N 泛型工具类
一、代码实现 通过封装 PriorityQueue 实现,PriorityQueue 本质上是完全二叉树实现的小根堆(相对来说,如果比较器反向比较则是大根堆)。 public class TopNUtil<E extends Comparable<E>> {private final PriorityQ…...

Java 后端面试指南
面试指南 TMD,一个后端为什么要了解那么多的知识,真是服了。啥啥都得了解 MySQL MySQL索引可能在以下几种情况下失效: 不遵循最左匹配原则:在联合索引中,如果没有使用索引的最左前缀,即查询条件中没有包含…...

142.环形链表 ||
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整…...

Nacos、Eureka、Zookeeper注册中心的区别
Nacos、Eureka和Zookeeper都是常用的注册中心,它们在功能和实现方式上存在一些不同。 Nacos除了作为注册中心外,还提供了配置管理、服务发现和事件通知等功能。Nacos默认情况下采用AP架构保证服务可用性,CP架构底层采用Raft协议保证数据的一…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
