【机器学习基础】一元线性回归(适合初学者的保姆级文章)
🚀个人主页:为梦而生~ 关注我一起学习吧!
💡专栏:机器学习 欢迎订阅!后面的内容会越来越有意思~
💡往期推荐:
【机器学习基础】机器学习入门(1)
【机器学习基础】机器学习入门(2)
【机器学习基础】机器学习的基本术语
【机器学习基础】机器学习的模型评估(评估方法及性能度量原理及主要公式)
💡本期内容:本篇文章开始机器学习的模型,我们从最简单的开始,所以从线性的开始,而线性模型中一元的最简单,最基础,所以先讲解一下一元线性回归~超级基础的文章,赶紧收藏学习吧!!!
文章目录
- 1 线性模型
- 2 一元线性回归
- 2.1 引例及模型表示
- 2.2 代价函数(Cost function)
- 3 一元梯度下降求参数
- 3.1 代价函数的简化
- 3.2 二元的代价函数
- 3.3 梯度下降
- 3.3.1 理解梯度下降
- 3.3.2 利用梯度下降求解线性回归
1 线性模型
给定由d个属性描述的示例x,其中xi是x在第i个属性上的取值,线性模型(linear model)试图学得一个通过属性的线性组合来进行预测的函数,即

一般用向量形式写成
w和b学得之后,模型就得以确定
2 一元线性回归
一元线性回归是一种统计分析方法,用于建立一个自变量和一个因变量之间的线性关系模型。在一元线性回归中,只有一个自变量(即解释变量)与一个因变量(即被解释变量)相关。
该模型的目标是找到一个最佳拟合直线,使得该直线能够最好地拟合已知的数据点并预测未知的数据点。最常用的评估拟合程度的指标是最小二乘法,它通过最小化观测值与拟合直线的差距的平方和来确定最佳拟合直线。
一元线性回归的模型可以表示为:Y = β₀ + β₁X + ε 其中,Y 是因变量,X 是自变量,β₀ 和 β₁ 是模型的系数,ε
是随机误差项。通过一元线性回归,我们可以估计自变量和因变量之间的关系,并进行预测和推断。
以上是官方解释,看不懂没事,我们来举一个经典的例子:
2.1 引例及模型表示
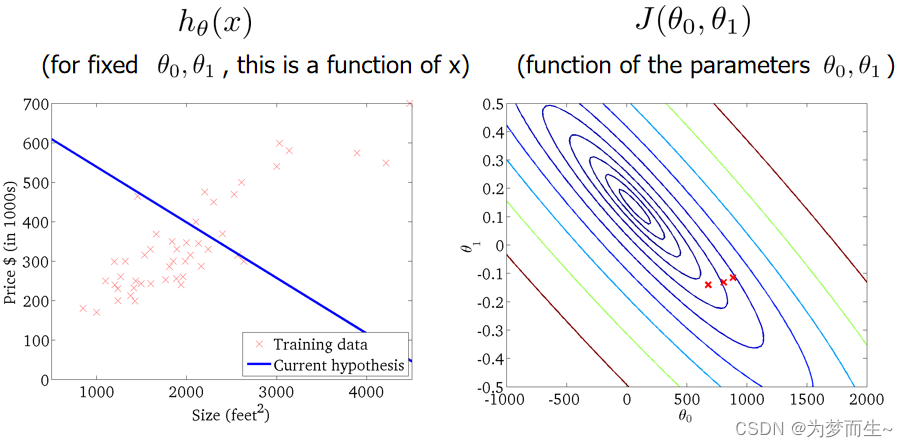
这个例子是关于预测房屋价格的,我们已知这样一个数据集:

横坐标表示房屋的面积,纵坐标表示房屋的价格。我们的目标是预测在给定房屋面积的情况下,房屋的价格是多少。例如,如果你的朋友的房子是1250平方英尺大小,你可以使用上面的数据集来预测其可能售价。那么,我们应该如何进行预测呢?
你可以构建一个模型,比如拟合一条直线,如上图所示。从这个模型来看,也许你可以告诉你的朋友,他可以以大约220000(美元)左右的价格卖掉这个房子。这其实就是一个回归问题的例子!

Notation:
- 𝑚:训练集中实例的数量
- 𝑥 :特征/输入变量
- 𝑦 :目标变量/输出变量
- (𝑥, 𝑦) :训练集中的实例
- (x(i), y(i)):第𝑖 个观察实例
- ℎ :学习算法的解决方案或函数也称为假设(hypothesis)
ℎ是一个函数,也是模型,代表的是从输入到输出的一个映射。这里输入是房屋尺寸大小,输出是房屋的价格。

在一元线性回归模型中如何表示h呢?

这里表示的就是单变量(一元)线性回归,其图像描述如下图所示:

回到例子中,我们需要借助h来预测房价。实际上 ,我们是要将训练集(已知的部分数据)“喂”给我们的学习算法,进而学习得到一个函数ℎ,然后将我们要预测的房屋的尺寸作为输入变量输入给ℎ,预测出该房屋的交易价格作为输出变量输出为结果。这个过程类似于在中学学到的求解直线方程,只是需要多次迭代。
那这个迭代过程究竟跟我们中学阶段的求解有什么区别呢?这里就要引出下面这个概念:
2.2 代价函数(Cost function)
对于一元线性函数,每一对参数都可以得到一种曲线的画法
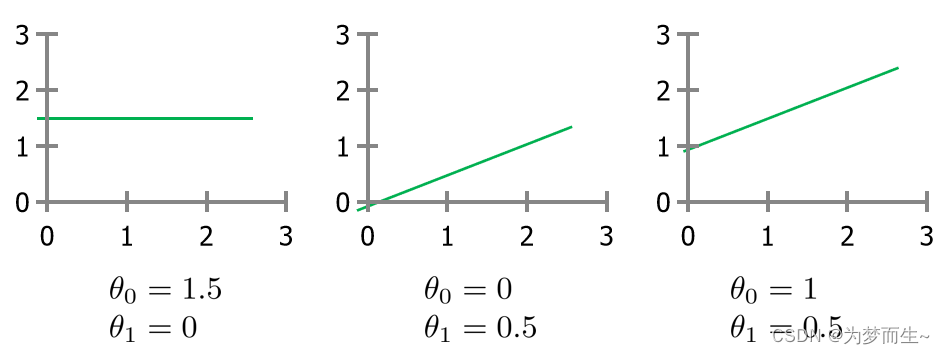
那么哪一种是最适合的呢?我们用假设函数来表示我们预测结果的模型。那么,这个模型好还是不好呢?我们需要有一个判别标准,这个标准就叫作代价函数。其表示形式如下:

对于代价函数的解释:
- 通过训练集我们可以得到假设函数h,即我们建立的模型,
- y是在这个点相应的ground truth。
- 通过输入测试集的自变量向函数h和y,得出预测出来的结果与实际的结果,让两者相减得到误差,通过误差可以看出我们预测的结果好还是不好。
- 求和再平方相当于求他们的方差,即预测值与真实值的差距的波动程度
- 们的最终目标就是最小化代价函数

那么我们现在的问题就转化为了如何利用训练集最小化代价函数
3 一元梯度下降求参数
如何求解代价函数呢?我们通常使用梯度下降的方法。
3.1 代价函数的简化
我们先理解含有一个参数的代价函数。

下面是当 𝜃1 = 1时的代价函数与假设函数

下面是 𝜃1 = 0.5时的曲线

下面做出 𝜃1 = 0 时的曲线并把代价函数所有的点连起来
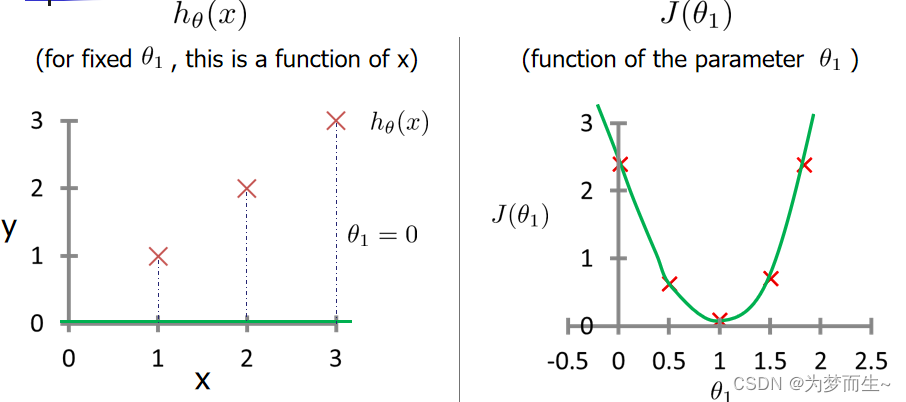
由图像我们可以知道,当J( θ 1 \theta _{1} θ1)取最小值时的参数所对应的假设函数是拟合数据最好的直线。
3.2 二元的代价函数
上面是之含有一个参数的代价函数,这里我们把另一个参数加上去,看看怎么求解:

再利用上面的方法,尝试每一个特殊的点,得到代价函数在坐标系中的位置后将他们连起来,我们就得到了一个二元代价函数,它是一个三维图形

同样利用上面的方法,遍历每一个参数 θ 0 \theta _{0} θ0, θ 1 \theta _{1} θ1,找到使得代价函数最小的参数。


多了一个参数相当于多了一个维度,图像也由一开始的二维拓展到了三维。求代价函数的最小值仍然是我们的目标。
可是要遍历的点太多了,我们怎么知道哪里是最小的点呢?下面介绍求代价函数最小值的方法:梯度下降
3.3 梯度下降
梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降是最常采用的方法之一。
3.3.1 理解梯度下降
举个例子,梯度下降法就是从山顶找一条最短的路走到山谷最低的地方。在这个过程中,每次都会沿着当前点的梯度方向(即函数在该点的斜率)走一步,逐步向最低点靠近。在机器学习中,基于基本的梯度下降法发展了两种梯度下降方法,分别为随机梯度下降法和批量梯度下降法。

那么具体到一元线性回归的代价函数,我们如何使用梯度下降呢?
3.3.2 利用梯度下降求解线性回归
接下来我们让梯度下降与线性回归相结合(关键在于对代价函数求偏导):
其主要思想如下:

其中𝑎是学习率(learning rate),它决定了我们沿着能让代价函数下降程度最大的方向 向下迈出的步子有多大,在批量梯度下降中,我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。

偏导 ( φ φ θ j J ( θ ) ) (\frac{\varphi }{\varphi \theta _{j}}J(\theta )) (φθjφJ(θ))的目的是为了确定下山的方向

当偏导大于0或小于0时代表了函数的不同增长趋势,与导数的意义相同
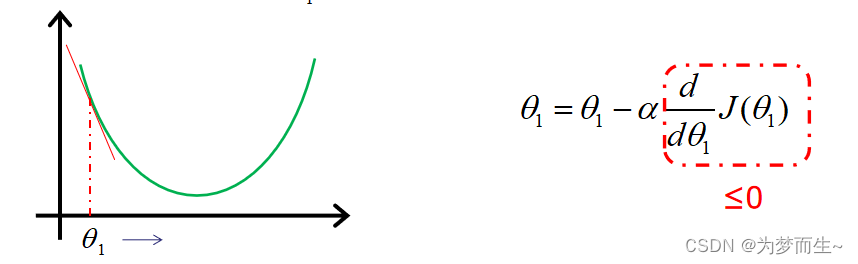
每走一步(每一次迭代)我们都需要确定新的参数,因为只有更新了参数才能确定下一步的方向。
每走一步都计算其梯度,经过不断的迭代,最终就可以找到最小值了。
公式的推导:


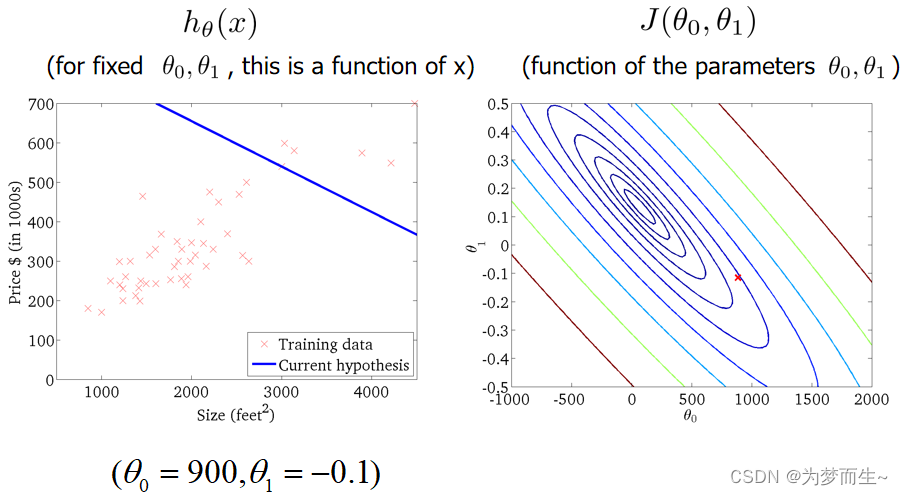
这样,我们就可以通过迭代,更快的找到最小值了

相关文章:

【机器学习基础】一元线性回归(适合初学者的保姆级文章)
🚀个人主页:为梦而生~ 关注我一起学习吧! 💡专栏:机器学习 欢迎订阅!后面的内容会越来越有意思~ 💡往期推荐: 【机器学习基础】机器学习入门(1) 【机器学习基…...

2024年软件测试岗位-面试
第一部分: 1、自我介绍:简历写到的快速描述,学校、学历、工作经验等(注意:不要过度优化简历,你不写别人可能会问,但你写了别人一定会问!) 第二部分: 1、功能测…...

【坑】Spring Boot整合MyBatis,一级缓存失效
一、Spring Boot整合MyBatis,一级缓存失效 1.1、概述 MyBatis一级缓存的作用域是同一个SqlSession,在同一个SqlSession中执行两次相同的查询,第一次执行完毕后,Mybatis会将查询到的数据缓存起来(缓存到内存中…...
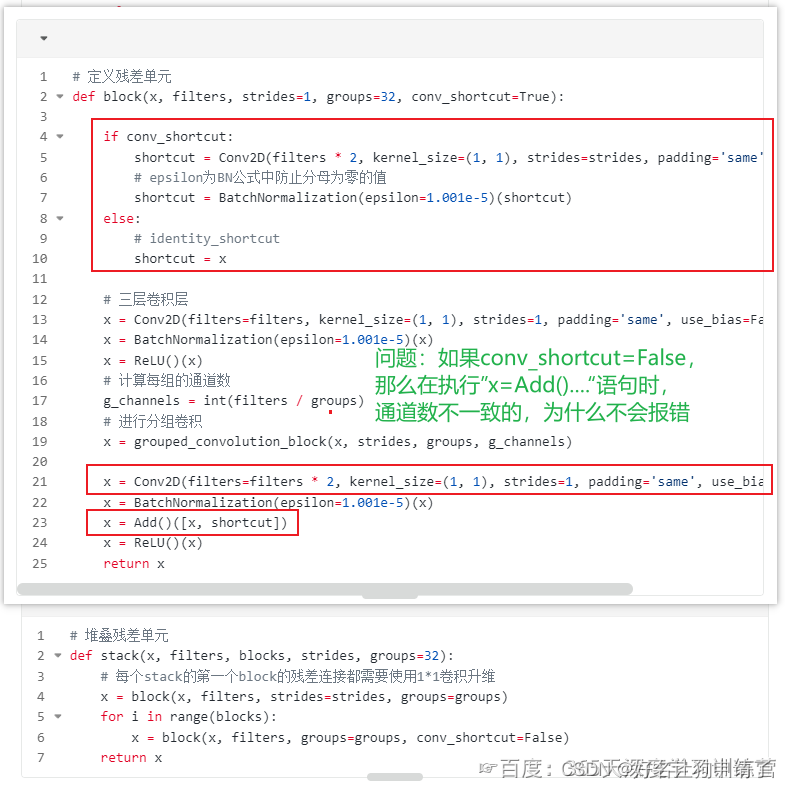
J7 - 对于ResNeXt-50算法的思考
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 | 接辅导、项目定制 J6周有一段代码如下 思考过程 首先看到这个问题的描述,想到的是可能使用了向量操作的广播机制然后就想想办法验证一下&…...
基础篇)
R3F(React Three Fiber)基础篇
之前一直在做ThreeJS方向,整理了两篇R3F(React Three Fiber)的文档,这是基础篇,如果您的业务场景需要使用R3F,您又对R3F不太了解,或者不想使用R3F全英文文档,您可以参考一下这篇&…...

torch\tensorflow在大语言模型LLM中的作用
文章目录 torch\tensorflow在大语言模型LLM中的作用 torch\tensorflow在大语言模型LLM中的作用 在大型语言模型(LLM)中,PyTorch和TensorFlow这两个深度学习框架起着至关重要的作用。它们为构建、训练和部署LLM提供了必要的工具和基础设施。 …...
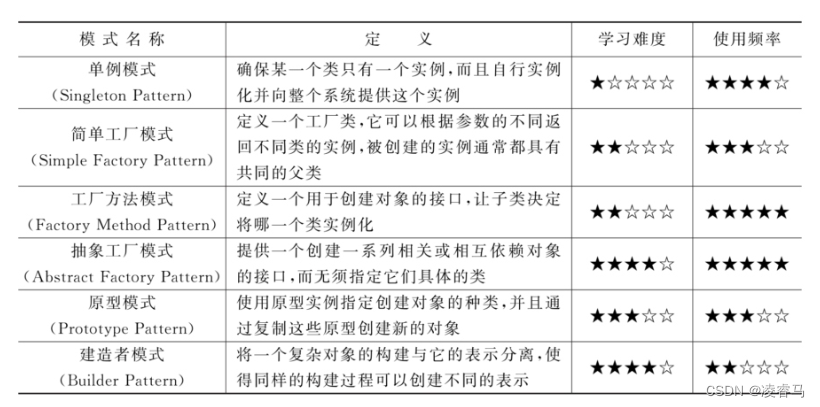
设计模式-创建型模式-单例模式
0 引言 创建型模式(Creational Pattern)关注对象的创建过程,是一类最常用的设计模式,每个创建型模式都通过采用不同的解决方案来回答3个问题:创建什么(What),由谁创建(W…...
备战蓝桥杯—— 双指针技巧巧答链表1
对于单链表相关的问题,双指针技巧是一种非常广泛且有效的解决方法。以下是一些常见问题以及使用双指针技巧解决: 合并两个有序链表: 使用两个指针分别指向两个链表的头部,逐一比较节点的值,将较小的节点链接到结果链表…...

微信小程序返回上一级页面并自动刷新数据
文章目录 前言一、获取小程序栈二、生命周期触发总结 前言 界面由A到B,在由B返回A,触发刷新动作 一、获取小程序栈 界面A代码 shuaxin(){//此处可进行接口请求从而实现更新数据的效果console.log("刷新本页面数据啦")},界面B代码 // 返回触…...

Spring⼯⼚创建复杂对象
文章目录 5. Spring⼯⼚创建复杂对象5.1 什么是复杂对象5.2 Spring⼯⼚创建复杂对象的3种⽅式5.2.1 FactoryBean 接口5.2.2 实例⼯⼚5.2.3 静态工厂 5.3 Spring 工厂的总结 6. 控制Spring⼯⼚创建对象的次数6.1 如何控制简单对象的创建次数6.2 如何控制复杂对象的创建次数6.3 为…...

Top-N 泛型工具类
一、代码实现 通过封装 PriorityQueue 实现,PriorityQueue 本质上是完全二叉树实现的小根堆(相对来说,如果比较器反向比较则是大根堆)。 public class TopNUtil<E extends Comparable<E>> {private final PriorityQ…...

Java 后端面试指南
面试指南 TMD,一个后端为什么要了解那么多的知识,真是服了。啥啥都得了解 MySQL MySQL索引可能在以下几种情况下失效: 不遵循最左匹配原则:在联合索引中,如果没有使用索引的最左前缀,即查询条件中没有包含…...

142.环形链表 ||
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整…...

Nacos、Eureka、Zookeeper注册中心的区别
Nacos、Eureka和Zookeeper都是常用的注册中心,它们在功能和实现方式上存在一些不同。 Nacos除了作为注册中心外,还提供了配置管理、服务发现和事件通知等功能。Nacos默认情况下采用AP架构保证服务可用性,CP架构底层采用Raft协议保证数据的一…...
CSS重点知识整理1
目录 1 平面位移 1.1 基本使用 1.2 单独方向的位移 1.3 使用平面位移实现绝对位置居中 2 平面旋转 2.1 基本使用 2.2 圆点转换 2.3 多重转换 3 平面缩放 3.1 基本使用 3.2 渐变的使用 4 空间转换 4.1 空间位移 4.1.1 基本使用 4.1.2 透视 4.2 空间旋转 4.3 立…...
【Langchain多Agent实践】一个有推销功能的旅游聊天机器人
【LangchainStreamlit】旅游聊天机器人_langchain streamlit-CSDN博客 视频讲解地址:【Langchain Agent】带推销功能的旅游聊天机器人_哔哩哔哩_bilibili 体验地址: http://101.33.225.241:8503/ github地址:GitHub - jerry1900/langcha…...
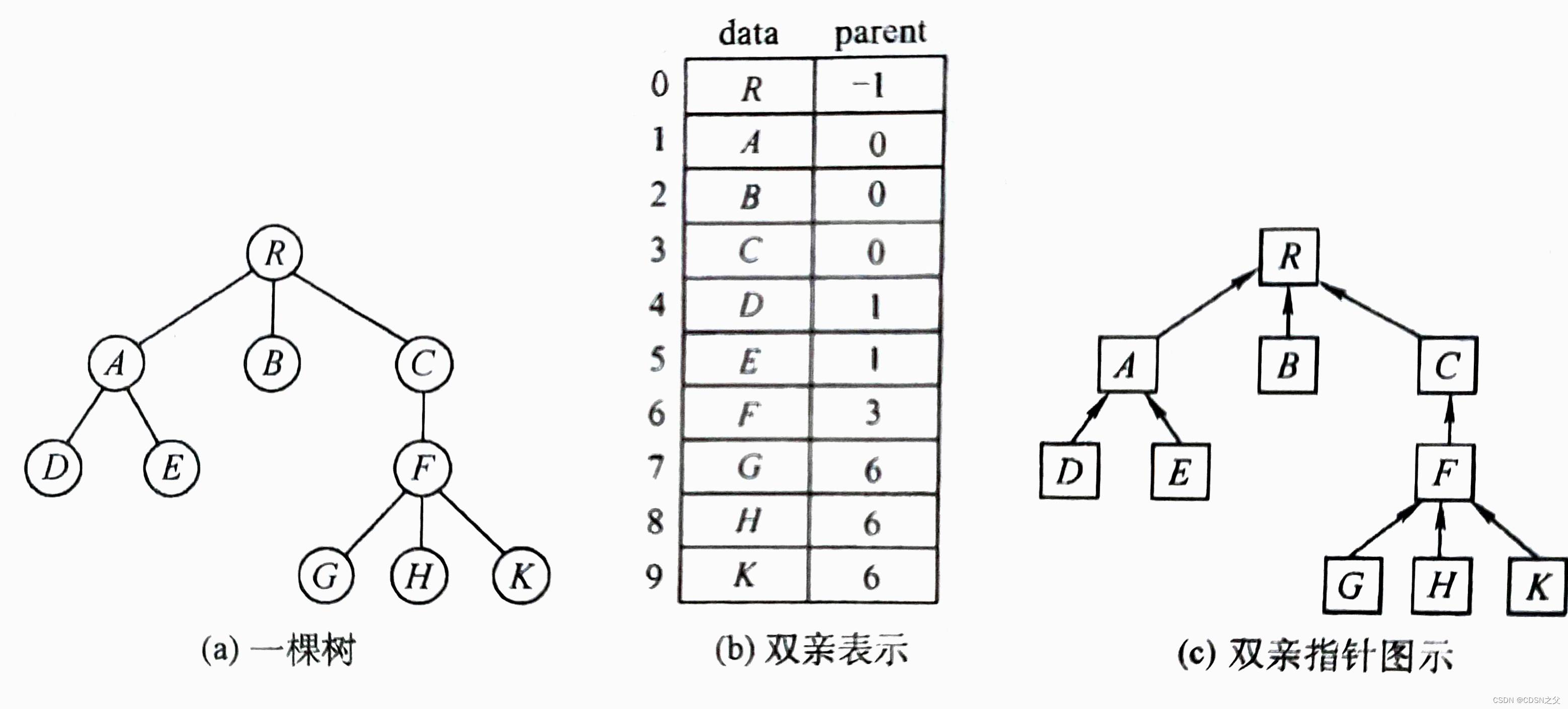
算法学习(十二)并查集
并查集 1. 概念 并查集主要用于解决一些 元素分组 问题,通过以下操作管理一系列不相交的集合: 合并(Union):把两个不相交的集合合并成一个集合 查询(Find):查询两个元素是否在同一…...
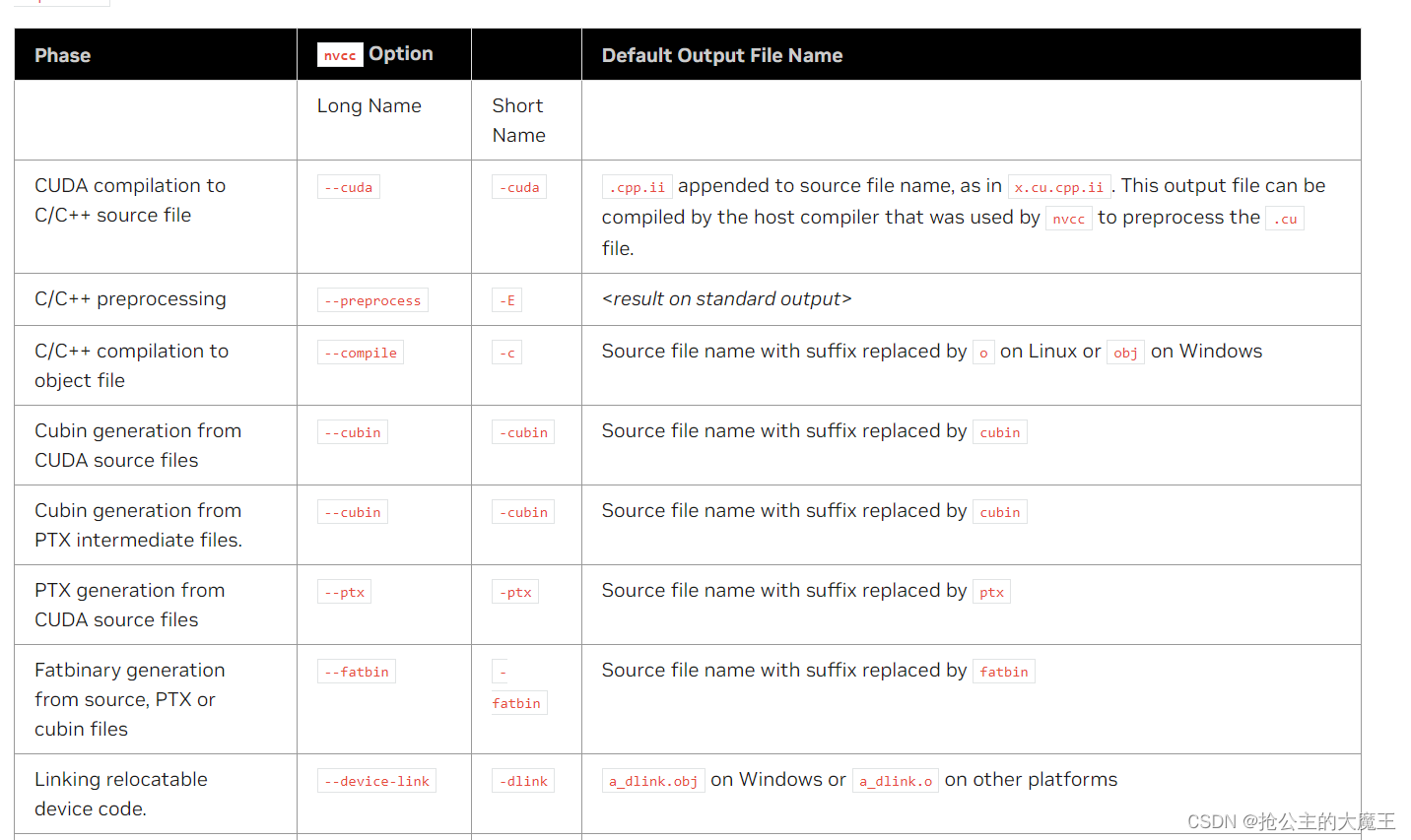
TensorRT及CUDA自学笔记003 NVCC及其命令行参数
TensorRT及CUDA自学笔记003 NVCC及其命令行参数 各位大佬,这是我的自学笔记,如有错误请指正,也欢迎在评论区学习交流,谢谢! NVCC是一种编译器,基于一些命令行参数可以将使用PTX或C语言编写的代码编译成可…...

数据库管理-第154期 Oracle Vector DB AI-06(20240223)
数据库管理154期 2024-02-23 数据库管理-第154期 Oracle Vector DB & AI-06(20240223)1 环境准备创建表空间及用户TNSNAME配置 2 Oracle Vector的DML操作创建示例表插入基础数据DML操作UPDATE操作DELETE操作 3 多Vector列表4 固定维度的向量操作5 不…...

解决uni-app vue3 nvue中使用pinia页面空白问题
main.js中,最关键的就是Pinia要return出去的问题,至于原因嘛! 很忙啊,先用着吧 import App from ./App import * as Pinia from pinia import { createSSRApp } from vue export function createApp() {const app createSSRApp(App);app.us…...

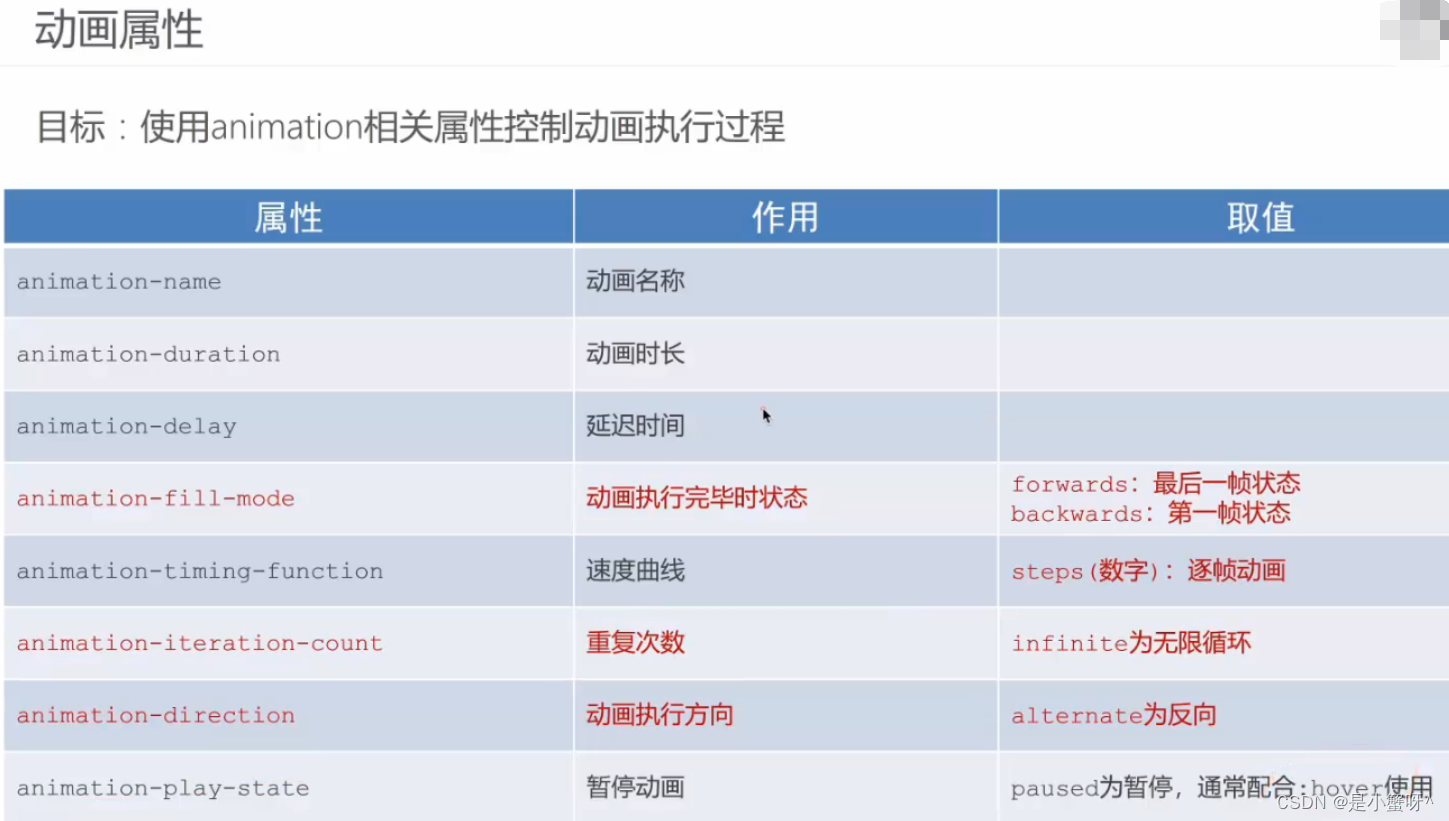
以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
