Codeforces Round 240 (Div. 1) C. Mashmokh and Reverse Operation(分治+逆序对)
原题链接:C. Mashmokh and Reverse Operation
题目大意:
给出一个长度为 2 n 2^{n} 2n 的正整数数组 a a a ,再给出 m m m 次操作。
每次操作给出一个数字 q q q ,把数组分为 2 n − q 2^{n-q} 2n−q 个长度为 2 q 2^{q} 2q 的段,然后每段执行一次翻转操作,操作完后输出当前数组的逆序对数量。
分段操作: [ a 1 , a 2 , . . . , a 2 q ] , [ a 2 q + 1 , a 2 q + 2 , . . . , a 2 q + 1 ] , . . . , [ a 2 n − 1 + 1 , a 2 n − 1 + 2 , . . . , a 2 n ] [a_{1},a_{2},...,a_{2^q}],[a_{2^{q}+1},a_{2^{q}+2},...,a_{2^{q+1}}],...,[a_{2^{n-1}+1},a_{2^{n-1}+2},...,a_{2^{n}}] [a1,a2,...,a2q],[a2q+1,a2q+2,...,a2q+1],...,[a2n−1+1,a2n−1+2,...,a2n]
翻转操作: [ a 2 q , a 2 q − 1 , . . . , a 1 ] , [ a 2 q + 1 , a 2 q − 1 , . . . , a 2 q + 1 ] , . . . , [ a 2 n , a 2 n − 1 , . . . , a 2 n − 1 + 1 ] [a_{2^{q}},a_{2^{q}-1},...,a_{1}],[a_{2^{q+1}},a_{2^{q}-1},...,a_{2^{q}+1}],...,[a_{2^{n}},a_{2^{n}-1},...,a_{2^{n-1}+1}] [a2q,a2q−1,...,a1],[a2q+1,a2q−1,...,a2q+1],...,[a2n,a2n−1,...,a2n−1+1]
每次操作会改变原数组,并且都要输出操作完后逆序对的数量。
解题思路:
很有意思的分治归并排序题。
首先发现我们数组长度是 2 2 2 的次幂,且每次分段长度也都是 2 2 2 的次幂,暗示我们可以向着分治的方向去思考。
我们知道:逆序对 + + + 顺序对 = n ⋅ ( n − 1 ) 2 =\frac{n \cdot(n-1)}{2} =2n⋅(n−1) 其中 n n n 为区间长度。
我们将一个区间翻转时,本质上就是将逆序对的值和顺序对的值交换了一下,因为本来逆序的翻转之后就变成顺序的了。
这样类似将数组分成一段段的 2 2 2 次幂长度,我们考虑可以考虑类似归并排序的分治方法。
归并排序是在排序的过程中同时算出每一层的逆序对,然后相加每层得到的逆序对,从而得到整个原数组的逆序对的。
假设原数组 a a a 为 [ 4 , 5 , 7 , 1 , 3 , 6 , 8 , 2 ] [4,5,7,1,3,6,8,2] [4,5,7,1,3,6,8,2] ,我们画出归并排序树看看:
3 : [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 ] 7 3:[1,2,3,4,5,6,7,8]^{7} 3:[1,2,3,4,5,6,7,8]7
2 : [ 1 , 4 , 5 , 7 ] 2 , [ 2 , 3 , 6 , 8 ] 2 2:[1,4,5,7]^{2},[2,3,6,8]^{2} 2:[1,4,5,7]2,[2,3,6,8]2
1 : [ 4 , 5 ] 0 , [ 1 , 7 ] 1 , [ 3 , 6 ] 0 , [ 2 , 8 ] 1 1:[4,5]^{0},[1,7]^{1},[3,6]^{0},[2,8]^{1} 1:[4,5]0,[1,7]1,[3,6]0,[2,8]1
0 : [ 4 ] , [ 5 ] , [ 7 ] , [ 1 ] , [ 3 ] , [ 6 ] , [ 8 ] , [ 2 ] 0:[4],[5],[7],[1],[3],[6],[8],[2] 0:[4],[5],[7],[1],[3],[6],[8],[2]
(右上角角标为将该层排好序时得到的逆序对数量,叶子层(第 0 0 0 层)均为 0 0 0 就不做标记了)
那么总的逆序对数就是所有层角标相加之和: 7 + 2 + 2 + 0 + 1 + 0 + 1 = 13 7+2+2+0+1+0+1=13 7+2+2+0+1+0+1=13 对。
我们考虑将区间长度为 2 1 2^{1} 21 的段全翻转,看看会造成什么影响。
3 : [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 ] 7 3:[1,2,3,4,5,6,7,8]^{7} 3:[1,2,3,4,5,6,7,8]7
2 : [ 1 , 4 , 5 , 7 ] 2 , [ 2 , 3 , 6 , 8 ] 2 2:[1,4,5,7]^{2},[2,3,6,8]^{2} 2:[1,4,5,7]2,[2,3,6,8]2
1 ′ : [ 4 , 5 ] 1 , [ 1 , 7 ] 0 , [ 3 , 6 ] 1 , [ 2 , 8 ] 0 1':[4,5]^{1},[1,7]^{0},[3,6]^{1},[2,8]^{0} 1′:[4,5]1,[1,7]0,[3,6]1,[2,8]0
0 ′ : [ 5 ] , [ 4 ] , [ 1 ] , [ 7 ] , [ 6 ] , [ 3 ] , [ 2 ] , [ 8 ] 0':[5],[4],[1],[7],[6],[3],[2],[8] 0′:[5],[4],[1],[7],[6],[3],[2],[8]
那么总的逆序对数就是 7 + 2 + 2 + 1 + 0 + 1 + 0 = 13 7+2+2+1+0+1+0=13 7+2+2+1+0+1+0=13 对。
可以发现,我们只有在第 1 → 0 1 \rightarrow 0 1→0 层往下的所有层逆序对被改变了,即顺序对和逆序对交换了,而其他层 n → 2 n \rightarrow 2 n→2 层则无变化。
因为归并到第 0 → i 0 \rightarrow i 0→i 层前,其下的所有层是在做 边排序边计算 的过程,因此无论其下层的顺序是怎么样的,最终数组 排序 到到第 i i i 层时的状态都是唯一确定的,不会影响到上一层。
比如我们修改前的第 1 1 1 层,和我们原数组的第 1 1 1 层状态是相同的,只有逆序对和顺序对的角标被改变了。
同理,无论按何种顺序如何翻转第 2 q 2^{q} 2q 层,其只会影响第 0 → q 0 \rightarrow q 0→q 的逆序对状态,而不会影响第 q + 1 → n q+1 \rightarrow n q+1→n 层逆序对的状态。
因此,我们先对原数组做一次归并排序,同时记录每一层的逆序对状态,和顺序对状态。
对每次的修改,对 1 → q 1 \rightarrow q 1→q 层直接交换顺序对和逆序对的值(第 0 0 0 层全是 0 0 0 ,可以不管),其余不变(或者用 2 n − q ⋅ 2 q ⋅ ( 2 q − 1 ) 2 − 2^{n-q} \cdot \frac{2^{q} \cdot (2^{q}-1)}{2}- 2n−q⋅22q⋅(2q−1)−当前层逆序对之和,不过有个 2 2 2 的次幂,比较麻烦)。
交换完后,统计所有层的逆序对之和就是我们的答案了。
时间复杂度: O ( n log n + q log n ) O(n \log n+q \log n) O(nlogn+qlogn)
AC代码:
#include <bits/stdc++.h>
using namespace std;using PII = pair<int, int>;
using i64 = long long;void solve() {int n;cin >> n;vector<int> a((1 << n) + 1);for (int i = 1; i <= (1 << n); ++i) {cin >> a[i];}vector cnt(n + 1, vector<i64>(2));vector<int> b(1 << n);auto Msort = [&](auto self, int l, int r, int dep) -> void {if (l >= r) return;int mid = l + r >> 1, i = l, j = mid + 1, k = 0;self(self, l, mid, dep - 1), self(self, mid + 1, r, dep - 1);//求顺序对while (i <= mid && j <= r) {if (a[i] < a[j]) {cnt[dep][1] += r - j + 1;++i;} else {++j;}}//求逆序对并同时将数组排序i = l, j = mid + 1;while (i <= mid && j <= r) {if (a[i] > a[j]) {cnt[dep][0] += mid - i + 1;b[k++] = a[j++];} else {b[k++] = a[i++];}}while (i <= mid) {b[k++] = a[i++];}while (j <= r) {b[k++] = a[j++];}for (i = l, j = 0; i <= r; ++i, ++j) {a[i] = b[j];}};Msort(Msort, 1, 1 << n, n);int q;cin >> q;for (int i = 1; i <= q; ++i) {int d;cin >> d;i64 ans = 0;//修改d层 则将 [1, d] 层的值全部交换一下for (int j = 1; j <= n; ++j) {if (j <= d) {swap(cnt[j][0], cnt[j][1]);}ans += cnt[j][0];}cout << ans << '\n';}
}signed main() {ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int t = 1; //cin >> t;while (t--) solve();return 0;
}
相关文章:
 C. Mashmokh and Reverse Operation(分治+逆序对))
Codeforces Round 240 (Div. 1) C. Mashmokh and Reverse Operation(分治+逆序对)
原题链接:C. Mashmokh and Reverse Operation 题目大意: 给出一个长度为 2 n 2^{n} 2n 的正整数数组 a a a ,再给出 m m m 次操作。 每次操作给出一个数字 q q q ,把数组分为 2 n − q 2^{n-q} 2n−q 个长度为 2 q 2^{q} 2…...
SpringBoot整合JDBC(一)JDBC组件的自动装配)
SpringBoot源码解读与原理分析(三十二)SpringBoot整合JDBC(一)JDBC组件的自动装配
文章目录 前言第10章 SpringBoot整合JDBC10.1 SpringBoot整合JDBC的项目搭建10.1.1 初始化数据库10.1.2 整合项目10.1.2.1 导入JDBC和MySQL驱动依赖10.1.2.2 配置数据源 10.1.3 编写业务代码10.1.3.1 编写与t_user表对应的实体类User10.1.3.2 编写Dao层代码10.1.3.3 编写Servic…...
petalinux_zynq7 驱动DAC以及ADC模块之五:nodejs+vue3实现web网页波形显示
前文: petalinux_zynq7 C语言驱动DAC以及ADC模块之一:建立IPhttps://blog.csdn.net/qq_27158179/article/details/136234296petalinux_zynq7 C语言驱动DAC以及ADC模块之二:petalinuxhttps://blog.csdn.net/qq_27158179/article/details/1362…...

Android java中内部类的使用
一.成员内部类 实验1:成员内部类 class Outer {private int a 10;class Inner {public void printInfo(){System.out.println("a "a);}}}public class InnerDemo {public static void main(String args[]) {Outer o new Outer();Outer.Inner i o.new…...
llm的inference(二)
文章目录 Tokenizer分词1.单词分词法2.单字符分词法3.子词分词法BPE(字节对编码,Byte Pair Encoding)WordPieceUnigram Language Model(ULM) embedding的本质推理时的一些指标参考链接 Tokenizer 在使用模型前,都需要将sequence过一遍Tokenizer…...

pytorch -- torch.nn.Module
基础 torch.nn 是 PyTorch 中用于构建神经网络的模块。nn.Module包含网络各层的定义及forward方法。 在用户自定义神经网络时,需要继承自nn.Module类。通过继承 nn.Module 类,您可以创建自己的神经网络模型,并定义模型的结构和操作。 torch.n…...

Microsoft Edge 越用越慢、超级卡顿?网页B站播放卡顿?
记录10个小妙招 Microsoft Edge 启动缓慢、菜单导航卡顿、浏览响应沉闷?这些情况可能是由于系统资源不足或浏览器没及时更新引起的。接下来,我们将介绍 10 种简单的方法,让 Edge 浏览器的速度重新起飞。 基础检查与问题解决 如果 Microsoft…...

XGB-9: 分类数据
从1.5版本开始,XGBoost Python包为公共测试提供了对分类数据的实验性支持。对于数值数据,切分条件被定义为 v a l u e < t h r e s h o l d value < threshold value<threshold ,而对于分类数据,切分的定义取决于是否使用…...

FreeRTOS学习第8篇--同步和互斥操作引子
目录 FreeRTOS学习第8篇--同步和互斥操作引子同步和互斥概念实现同步和互斥的机制PrintTask_Task任务相关代码片段CalcTask_Task任务相关代码片段实验现象本文中使用的测试工程 FreeRTOS学习第8篇–同步和互斥操作引子 本文目标:学习与使用FreeRTOS中的同步和互斥操…...
,c++STL算法的理解与使用(sort, find, binary_search等))
c++STL容器的使用(vector, list, map, set等),c++STL算法的理解与使用(sort, find, binary_search等)
cSTL容器的使用(vector, list, map, set等) 在C的STL(Standard Template Library)中,容器是重要的一部分,它们提供了各种数据结构来存储和管理数据。以下是一些常见的STL容器及其使用方法的简要说明&#x…...

选择VR全景行业,需要了解哪些内容?
近年来,随着虚拟现实、增强现实等技术的持续发展,VR全景消费市场得以稳步扩张。其次,元宇宙行业的高速发展,也在进一步拉动VR全景技术的持续进步,带动VR产业的高质量发展。作为一种战略性的新兴产业,国家和…...

830. 单调栈
Problem: 830. 单调栈 文章目录 思路解题方法复杂度Code 思路 这是一个单调栈的问题。单调栈是一种特殊的栈结构,它的特点是栈中的元素保持单调性。在这个问题中,我们需要找到每个元素左边第一个比它小的元素,这就需要使用到单调递增栈。 我们…...

H5 个人引导页官网型源码
H5 个人引导页官网型源码 源码介绍:源码无后台、无数据库,H5自检测适应、无加密,直接修改可用。 源码含有多选项,多功能。可展示自己站点、团队站点。手机电脑双端。 下载地址: https://www.changyouzuhao.cn/1434.…...
【Linux】部署前后端分离项目---(Nginx自启,负载均衡)
目录 前言 一 Nginx(自启动) 2.1 Nginx的安装 2.2 设置自启动Nginx 二 Nginx负载均衡tomcat 2.1 准备两个tomcat 2.1.1 复制tomcat 2.1.2 修改server.xml文件 2.1.3 开放端口 2.2 Nginx配置 2.2.1 修改nginx.conf文件 2.2.2 重启Nginx服务 2…...
WPF Style样式设置
1.本window设置样式 <Window x:Class"WPF_Study.MainWindow"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x"http://schemas.microsoft.com/winfx/2006/xaml"xmlns:d"http://schemas.microsoft.com/expressi…...

【STM32】软件SPI读写W25Q64芯片
目录 W25Q64模块 W25Q64芯片简介 硬件电路 W25Q64框图 Flash操作注意事项 状态寄存器 编辑 指令集 INSTRUCTIONS编辑 编辑 SPI读写W25Q64代码 硬件接线图 MySPI.c MySPI.h W25Q64 W25Q64.c W25Q64.h W25Q64_Ins.h main.c 测试 SPI通信(W25…...

普通中小学校管理信息系统V1.1
普通中小学校管理信息系统 Ordinary Primary and Secondary Schools Management Information System 普通中小学校管理信息系统 Ordinary Primary and Secondary Schools Management Information System...

中国水果采摘机器人行业市场研究及发展趋势分析报告
全版价格:壹捌零零 报告版本:下单后会更新至最新版本 交货时间:1-2天 第一章 2016-2026年中国水果采摘机器人行业总概 1.1 中国水果采摘机器人行业发展概述 机器人技术的发展是一个国家高科技水平和工业自动化程度的重要标志和体现。机器…...

Linux多进程与信号
在多进程的服务程序中,如果子进程收到退出信号,子进程自行退出。如果父进程收到退出信号,应该先向全部的子进程发送退出信号,然后自己再退出。 演示demo程序 #include <iostream> // 包含输入输出流库,用于输…...

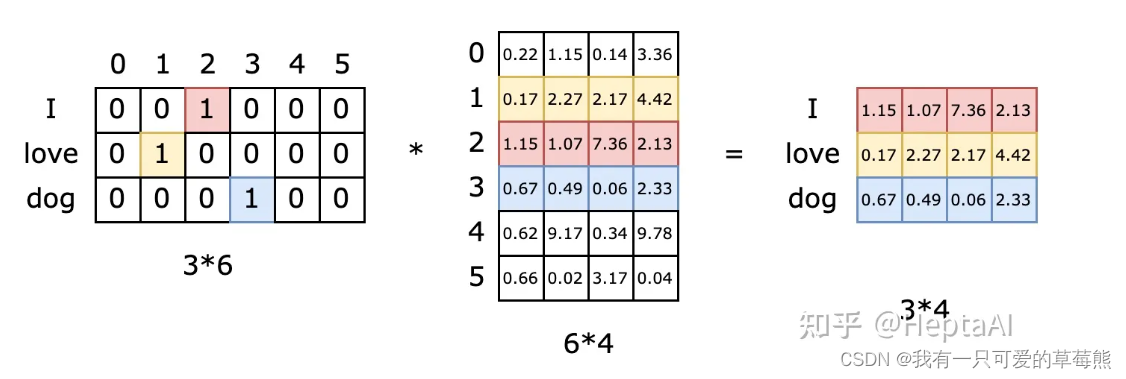
Self-attention与Word2Vec
Self-attention(自注意力)和 Word2Vec 是两种不同的词嵌入技术,用于将单词映射到低维向量空间。它们之间的区别: Word2Vec: Word2Vec 是一种传统的词嵌入(word embedding)方法,旨在为…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
