154、【动态规划】leetcode ——494. 目标和:回溯法+动态规划(C++版本)
题目描述



原题链接:494. 目标和
解题思路
(1)回溯法
本题的特点是nums中每个元素只能使用一次,分别试探加上nums[index]和减去nums[index],然后递归的遍历下一个元素index + 1。
class Solution {
public:int res = 0;void backtracking(vector<int>& nums, int target, int index) {if(index == nums.size()) {if(target == 0) res++;return ;}backtracking(nums, target - nums[index], index + 1);backtracking(nums, target + nums[index], index + 1);}int findTargetSumWays(vector<int>& nums, int target) {backtracking(nums, target, 0);return res;}
};
(2)动态规划
本题中的数都为非负数,目标要求是选取组成正数的数与负数的数,让其和为target,因此我们可以将这个题中的数划分为两个集合,一个是要组成正数的集合,设容量为pos,一个是要组成负数的集合,设容量为neg。
由题中要求可得pos - neg = target,pos + neg = sum,联立两式,可得2 * pos = target + sum,因此我们就可以进行第一个判定,当target + sum不为偶数时,可知一定不能组合出target直接返回false即可。当为偶数时,我们要找到可以组成pos(pos = (target + sum) / 2)的组合。问题就可以转变为,当背包容量为pos时,选取nums里的数,有多少种组合方式可填满背包。
- 动态规划五步曲:
(1)dp[j]含义: 装满背包容量为j的方式个数。
(2)递推公式: dp[j] += dp[j - nums[i]],装入nums[i]之前,容量为j - nums[i]时的方式个数dp[j - nums[i]],再加上装入nums[i]之后,容量为j时之前的方式个数dp[j],进而得到背包容量为j时,总的方式个数。
(3)dp数组初始化: dp[0] = 1,容量为0时,仅有一种方式可以成立,即选择数字0。
(4)遍历顺序: 先物品、再背包,内层按从大到小遍历的滚动数组。
(5)举例:
输入: nums: [1, 1, 1, 1, 1], S: 3
此时,正数最大为4,里面只有1,因此dp[j]长度为4。

class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sumNums = 0;for(int i = 0; i < nums.size(); i++) sumNums += nums[i];// target超过总和或者不满足pos为偶数的情况,直接返回0if(abs(target) > sumNums || (sumNums + target) % 2 != 0) return 0;int dp[10001] = {0};dp[0] = 1;int pos = (sumNums + target) / 2;for(int i = 0; i < nums.size(); i++) {for(int j = pos; j >= nums[i]; j--) {// 组合情况要累计dp[j] += dp[j - nums[i]];}}return dp[pos];}
};
参考文章:494. 目标和、目标和、目标和(详细C++代码动态规划详细思路分析)
相关文章:

154、【动态规划】leetcode ——494. 目标和:回溯法+动态规划(C++版本)
题目描述 原题链接:494. 目标和 解题思路 (1)回溯法 本题的特点是nums中每个元素只能使用一次,分别试探加上nums[index]和减去nums[index],然后递归的遍历下一个元素index 1。 class Solution { public:int res …...

MySQL-窗口函数
窗口函数概念常用窗口函数聚合窗口函数专用窗口函数语法OVER子句window_specwindow_name (命名窗口)partition_clause 分区order_clause 排序frame_clause 范围 (指定窗口大小)使用限制练习准备概念 窗口函数对一组查询执行类似于聚合的操作。然而&#…...

【C++设计模式】学习笔记(1):面向对象设计原则
目录 简介面向对象设计原则(1)依赖倒置原则(DIP)(2)开放封闭原则(OCP)(3)单一职责原则(SRP)(4)Liskov替换原则(LSP)(5)接口隔离原则(ISP)(6)优先使用对象组合,而不是类继承(7)封装变化点(8)针对接口编程,而不是针对实现编程结语简介 Hello! 非常感谢您阅读海…...

[测开篇]设计测试用例的方法如何正确描述Bug
文章目录为什么测试人员要写测试用例?怎样设计测试用例?(总的方面)1.基于需求设计测试用例(总的方面) 2.页面(总的方面) 3.非功能性测试(具体方面) 4.1 等…...

设计模式学习笔记--单例、建造者、适配器、装饰、外观、组合
以下内容根据以下网址及相关视频整理:Android设计模式之单例模式_谬谬清不给我取名字的博客-CSDN博客_android 单例模式 Android设计模式--单例模式的六种实现和单例模式讲解Volatile与Synchronized相关的并发_龙腾腾的博客-CSDN博客_android 单例 volatile java …...

English Learning - Day5 L1考前复习 2023.2.10 周五
English Learning - Day5 L1考前复习 2023.2.10 周五1 单选题:She has the face _________.2 单选题: The goals ________ he fought all his life no longer seemed important to him.3 单选题:Sales director is a position ______ communi…...

C. Prepend and Append
time limit per test 1 second memory limit per test 256 megabytes input standard input output standard output Timur initially had a binary string†† s� (possibly of length 00). He performed the following operation several (possibly zero)…...
javassm超市在线配送管理系统
为了解决用户便捷地在网上购物,本文设计和开发了一个超市管理系统。本系统是基于web架构设计,SSM框架 ,使用Mysql数据库管理,综合采用JSP模式来完成系统的相关功能。主要实现了管理员与用户的注册与登陆,个人中心、用户…...
)
Scratch少儿编程案例-多模式贪吃蛇(无尽和计时)
专栏分享 点击跳转=>Unity3D特效百例点击跳转=>案例项目实战源码点击跳转=>游戏脚本-辅助自动化点击跳转=>Android控件全解手册点击跳转=>Scratch编程案例👉关于作者...

谷歌蜘蛛池怎么搭建?Google蜘蛛池可以帮助谷歌排名吗?
本文主要分享关于谷歌蜘蛛池的搭建疑问,以及Google对谷歌排名的影响到底有多大。 本文由光算创作,有可能会被剽窃和修改,我们佛系对待这种行为吧。 谷歌蜘蛛池怎么搭建? 答案是:需要一个内链外链体系复杂的站群系统…...
Kubernetes集群-部署Java项目
Kubernetes集群-部署Java项目(SSG) k8s部署项目java流程图 第一步 打包制作镜像 打包 java源码: application.properties #在有pom.xml的路径下执行 mvn clean package制作镜像: 将刚才打包后的文件夹传到,装有dock…...

English Learning - Day54 作业打卡 2023.2.8 周三
English Learning - Day54 作业打卡 2023.2.8 周三引言1. 就算你不喜欢喝酒,也请尝一杯吧。2. 便纵有千种风情,更与何人说?——柳永《雨霖铃》 (来,挑战一下古诗词)3. 虽然忙,我也要参加会议。4. 无论发生什么…...

【Unity题】 1.矩阵旋转,欧拉旋转,四元数旋转各自的优缺点。2.StringBuilder和String的区别
1.矩阵旋转,欧拉旋转,四元数旋转各自的优缺点 矩阵旋转,欧拉旋转,四元数旋转是三种不同的旋转表示方法,下面是它们各自的优缺点: 矩阵旋转: 优点: 1.可以方便地实现复合旋转&…...
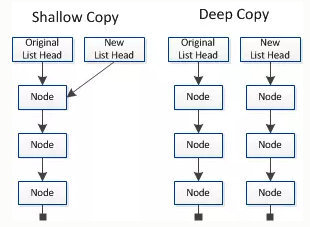
【C++面试问答】搞清楚深拷贝与浅拷贝的区别
问题 深拷贝和浅拷贝的区别是面试中的常见问题之一,对于不同的编程语言,这个问题的回答可能稍有差别,下面我们就来探索一下它们之间的异同吧。 先来看看在JavaScript对象的深拷贝与浅拷贝的区别: 浅拷贝:只是复制了…...
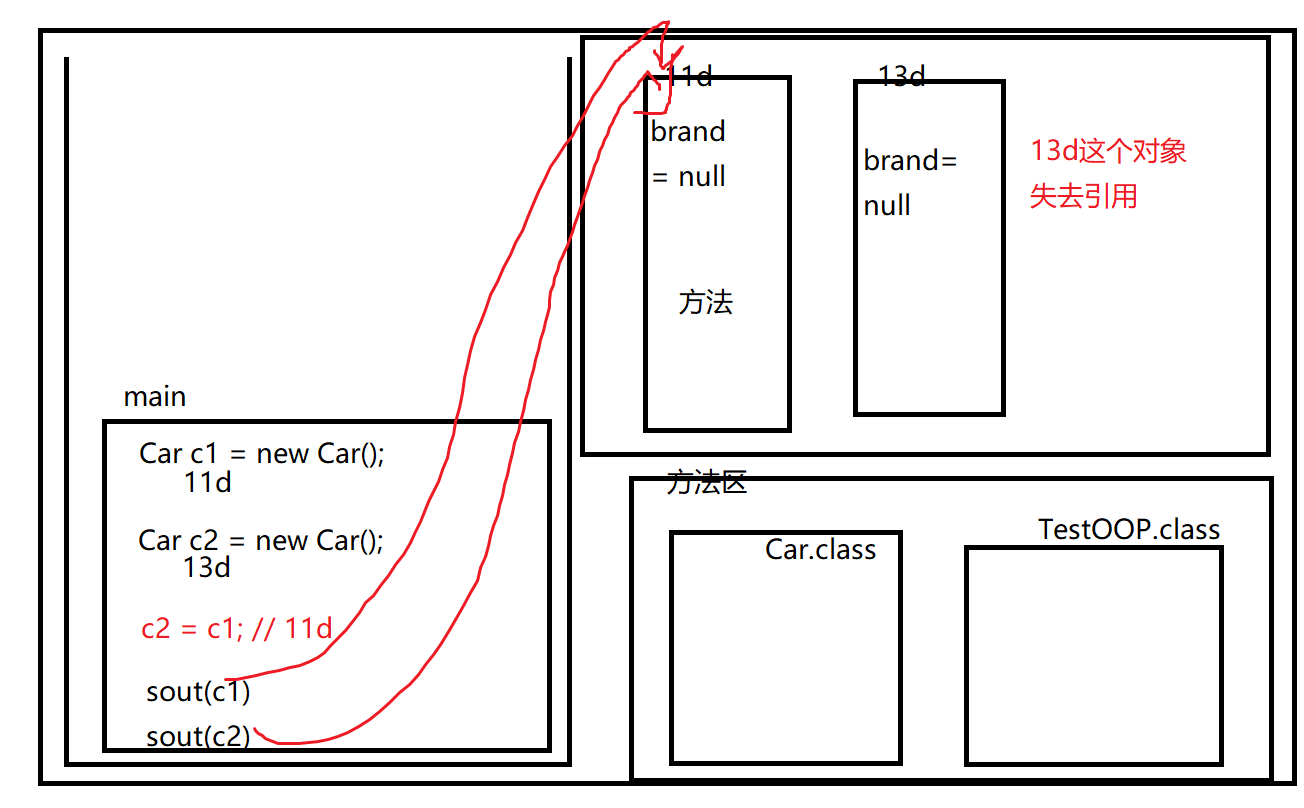
day10_面向对象基础
今日内容 零、 复习昨日 一、面向对象的概念 二、面向对象编程 三、内存图 零、 复习昨日 见晨考题 每日一数组题 写一个方法 用于合并两个int类型的数组 合并法则如下 {1,2,5,8,9}{1,3,0}---->{1,2,5,8,9,1,3,0} package com.qf.array;import java.util.Arrays;/*** --- 天…...
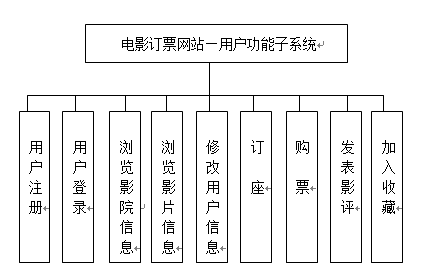
电影订票网站的设计与开发
技术:Java、JSP等摘要:随着科技的发展,时代的进步,互联网已经成为了人们生活中不可缺少的一部分,网上购物已然是一种时代的象征。纵观市场,电影行业的发展尤为迅速,电影种类和数量的增多导致客流…...

seata【SAGA模式】代码实践(细节未必完全符合saga的配置,仅参考)
seata SAGA模式: 代码仍然是上一篇AT模式的代码:AT模式 不需要undo_log表 下面开始: 首先,saga模式依靠状态机的json文件来执行整个流程,其中的开始节点的服务即TM,然后状态机需要依靠三张表࿰…...

面试题:Java锁机制
java对象包含了三个部分:对象头,实例数据和对齐填充。对象头又存放了:markWord和class point。classpoint :指向方法区,当前对象的类信息数据。markword:存储了很多和当前对象运行时的数据:例如…...
Springboot Web开发
文章目录一. 静态资源访问1. 配置静态资源访问前缀2. 修改默认静态资源存放目录3. Webjars4. 欢迎页支持5. 自定义Favicon二. 请求处理1. 路径变量2. 请求头处理3. 查询字符串处理4. 获取Cookie的值5. 获取请求体的值6. 获取请求域中的数据7. 矩阵变量一. 静态资源访问 只要静…...
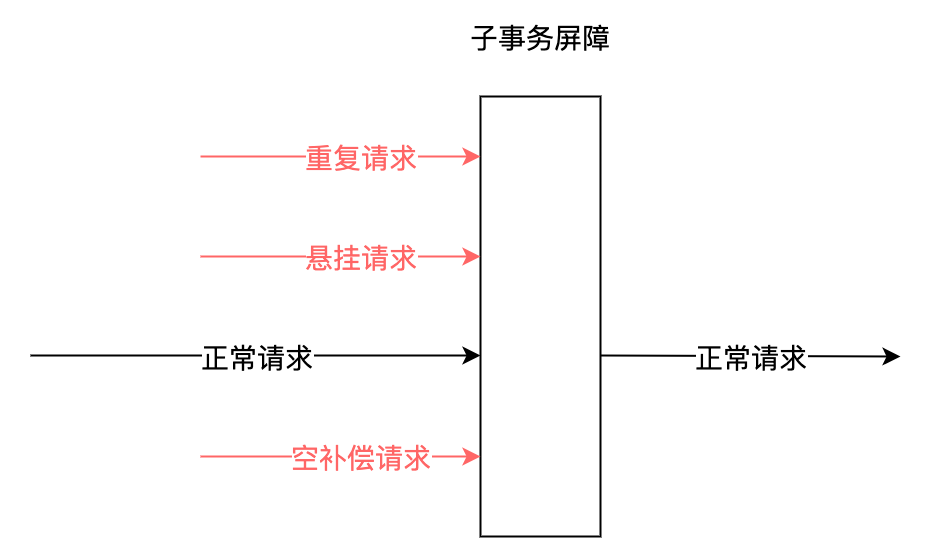
分布式事务 | 使用DTM 的Saga 模式
DTM 简介前面章节提及的MassTransit、dotnetcore/CAP都提供了分布式事务的处理能力,但也仅局限于Saga和本地消息表模式的实现。那有没有一个独立的分布式事务解决方案,涵盖多种分布式事务处理模式,如Saga、TCC、XA模式等。有,目前…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...
