我们为什么要用消息队列?
消息队列是系统设计中存在时间最长的中间件之一,从系统有通信需求开始,就产生了消息队列。
消息队列的使用场景
在日常系统设计与实现的过程中,下面3种场景会涉及到消息队列:
- 异步处理
- 流量控制
- 服务解耦
异步处理
典型的应用场景是秒杀系统,它要解决的核心问题是如何利用有限的服务器资源,尽可能多的处理短时间内的海量请求。
一般秒杀系统会包含下面的步骤:
- 风险控制
- 库存锁定
- 生成订单
- 短信通知
- 更新统计数据
在没有引入消息队列时,上述5个步骤会依次执行,在引入消息队列后,只要风险控制和库存锁定完成,那么就可以返回用户秒杀成功,后面的步骤和秒杀没有直接关联,我们可以在库存锁定完成后,向消息队列中发送用户和商品信息,之后的子系统会读取消息队列的消息,进行后续处理。
这秒杀场景中引入消息队列,带来两个好处:
- 可以更快的返回结果。
- 减少等待,实现步骤之间并行处理,提升性能。
流量控制
一个设计健壮的程序有自我保护能力,在海量请求下可以在自身能力范围内尽可能多的处理请求,拒绝处理不了的请求并且保证自身运行正常。
还是以秒杀场景为例,我们可以进一步调整设计思路,使用消息队列隔离网关和后端服务:
- 网关收到请求后,将请求放入到请求消息队列。
- 后端服务从请求消息队列中获取APP请求,完成后续秒杀处理过程,然后返回结果。
这样当海量请求到来时,不会直接冲击到后端的秒杀服务,而是堆积在消息队列中,后端服务按照自己的最大处理能力,从消息队列中消费请求进行处理。对于超时的请求可以直接丢弃,APP可以将其视为秒杀失败。
这其实就是流量控制中的“漏桶流量控制”,网关在这里充当了”漏桶“的角色。
这样的设计可以根据下游的处理能力自动调节流量,达到”削峰填谷“的目的,但是有两个问题:
- 增加了系统调用链环节,导致总体响应时间变长。
- 上下游系统都要将同步调用改为异步调用,增加了系统复杂度。
我们还可以使用“令牌桶”来控制流量。它的原理是:单位时间内只发放固定数量的令牌到令牌桶中,规定服务在处理请求前必须先从令牌桶中拿出一个令牌,如果令牌桶中没有令牌,则拒绝请求。这样就保证在单位时间内,能处理的请求不超过发放令牌的数量。
令牌桶可以简单地用一个有固定容量的消息队列+一个“令牌发生器”来实现:令牌发生器按照预估的处理能力,匀速生产令牌并放入令牌队列(如果队列满了就丢弃令牌),网关在收到请求时到令牌队列消费一个令牌,获取到令牌则继续调用后端服务,如果获取不到则等待或者返回失败。
服务解耦
消息队列还可以起到服务解耦的作用,例如订单是电商系统中比较核心的数据,当创建一个新订单时:
- 支付系统需要发起支付流程
- 风控系统需要审核订单的合法性
- 客服系统需要给用户发送短信
- 经营分析系统需要更新统计数据
- 。。。。。
这些订单下游的系统都需要实时获取订单数据,随着业务发展,这些订单下游系统会不断增加,不断变化,并且每个系统可能只需要订单数据的一个子集,负责订单服务的开发团队不得不花费很大精力,应付不断增加变化的下游系统,不停修改调试订单系统与这些下游系统的接口。任何一个下游系统接口变更,都需要订单模块重新上线,这是不可接受的。
问题的解决办法是所有的下游系统可以通过消息队列来和订单系统通信,引入消息队列后,订单服务在订单变化时发送一条消息到消息队列,所有订阅相关主题的下游系统都可以实时获得一份完整的订单数据。
这样无论下游系统如何变化,订单服务都无需做任何更改,实现了订单服务和下游服务的解耦。
除了上述三种典型场景,消息队列还可以应用到:
- 作为发布/订阅系统实现一个微服务级系统间的观察者模式
- 连接流计算任务和数据
- 用于将消息广播给大量接收者
消息队列并不是“银弹”,下面的场景就不适合用消息队列:
- 实时响应要求高
- 数据强一致性要求高
- 不能容忍数据或者消息丢失
在引入消息队列后,也可能带来一些新的问题,包括:
- 异步通信带来的延迟问题
- 增加了系统设计的复杂度
- 可能会产生数据不一致的问题
相关文章:

我们为什么要用消息队列?
消息队列是系统设计中存在时间最长的中间件之一,从系统有通信需求开始,就产生了消息队列。 消息队列的使用场景 在日常系统设计与实现的过程中,下面3种场景会涉及到消息队列: 异步处理流量控制服务解耦 异步处理 典型的应用场…...
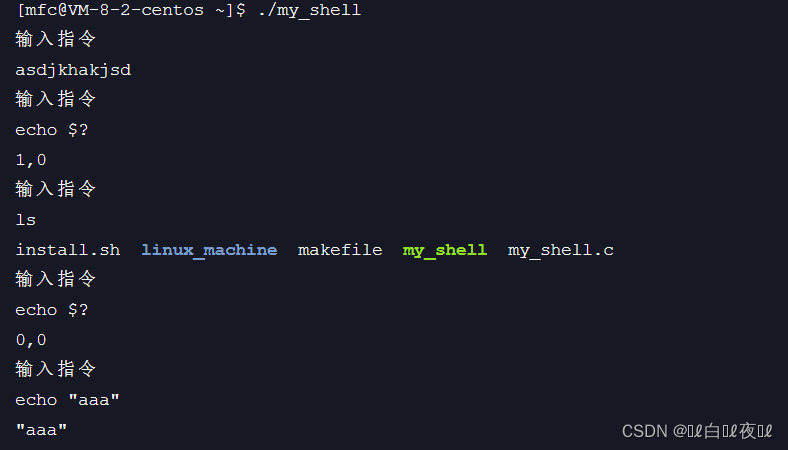
Linux进程控制
进程控制fork函数进程终止退出码常见的退出方式进程等待什么是进程等待,为什么要进程等待阻塞与非阻塞进程替换替换原理替换函数执行系统命令执行自己写的程序模拟实现简易的shellfork函数 fork函数是创建一个子进程,之前用过。 #include <unistd.h…...
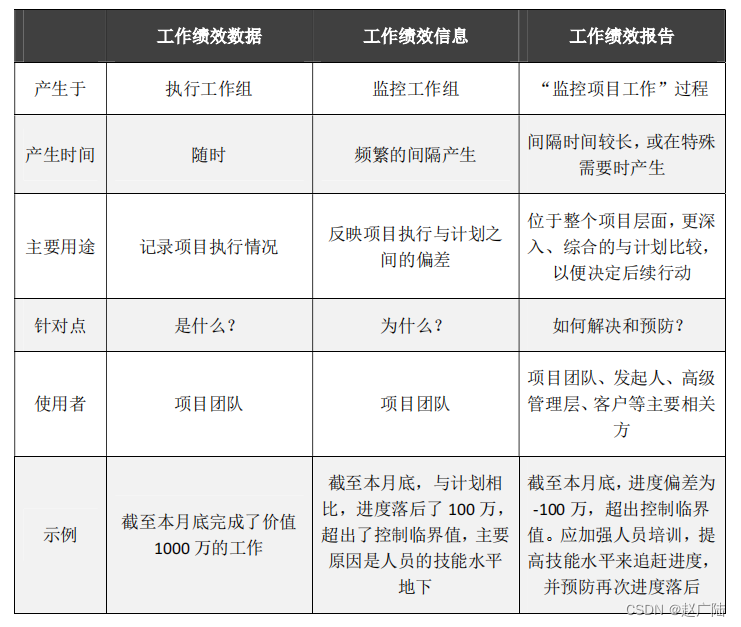
PMP项目管理引论介绍
目录1. 指南概述和目的1.1 项目管理标准1.2 道德与专业行为规范2 基本要素2.1 项目2.2 项目管理的重要性2.3 项目、项目集、项目组合以及运营管理之间的关系2.3.1 概述2.3.2. 项目组合与项目集管理2.3.3. 运营管理2.3.4. 组织级项目管理和战略2.3.5. 项目管理2.3.6. 运营管理与…...

计算机视觉废钢堆提取问题
计算机视觉废钢堆提取问题 背景介绍 在钢铁炼制中,废钢是非常重要的原料,不同等级废钢对于钢成品影响很大,因此需要对废钢进行正确分类。某废钢料场中,卸料区域布置了多个摄像头,用于拍摄卸料场中废钢堆,…...
)
判断水仙花数-课后程序(Python程序开发案例教程-黑马程序员编著-第二章-课后作业)
实例5:判断水仙花数 水仙花数是一个3位数,它的每位数字的3次幂之和等于它本身,例如13 53 33 153,153就是一个水仙花数。 本实例要求编写程序,实现判断用户输入的3位数是否为水仙花数的功能。 实例目标 掌握Pytho…...

目标检测: 数据增强代码详解
1. 常见的数据增强 1.1 翻转图像 左右水平翻转 假设图片的宽高为w,h,bdbox左上角A坐标为(x1,y1), 右下角B为(x2,y2)。经过左右水平翻转后,bdbox的左上角A1坐标(w-x2,y1) ,右下角B1坐标为(w-x1,y2)左右水平翻转的代码实现如下:from PIL import Image image = Image.open(i…...

第二讲:ambari编译复盘,如何实现一次性成功编译ambari
上节课我们已经讲解了如何成功编译ambari源码,安装ambari-server rpm包以及成功部署ambari。本节课我们来复盘一下上节课的编译过程,以及思考如何实现一次性成功编译ambari。 要想一次性成功编译ambari,那么就需要将预置工作做好,比如: maven镜像源配置,node_moudle模块…...

Windows下jdk安装与卸载-超详细的图文教程
jdk安装 下载jdk 由于现在主流就是jdk1.8,所以这里就下载jdk1.8进行演示。官方下载地址:https://www.oracle.com/java/technologies/downloads/#java8-windows。 官方下载需要注册oracle账号,国内下载有可能速度慢,若不想注册账…...

Jackson CVE-2018-5968 反序列化漏洞
0x00 前言 同CVE-2017-15095一样,是CVE-2017-7525黑名单绕过的漏洞,主要还是看一下绕过的调用链利用方式。 可以先看: Jackson 反序列化漏洞原理 或者直接看总结也可以: Jackson总结 影响版本:至2.8.11和2.9.x至…...
考试中一道大部分同学都会做错的题目)
解析MySQL 8.0 OCP(1Z0-908)考试中一道大部分同学都会做错的题目
一个用户有下面的权限: mysql>SHOW GRANTS FOR jsmith;---------------------------------------------------------------------- | Grants for jsmith% | ----------------------------------------------------------…...

Java死锁
什么是死锁? 多个线程同时被阻塞,它们中的一个或者全部都在等待某个资源被释放。由于线程被无限期地阻塞,因此程序不可能正常终止。 死锁的必要条件: 1、互斥条件:该资源任意一个时刻只由一个线程占用。 2、请求与…...
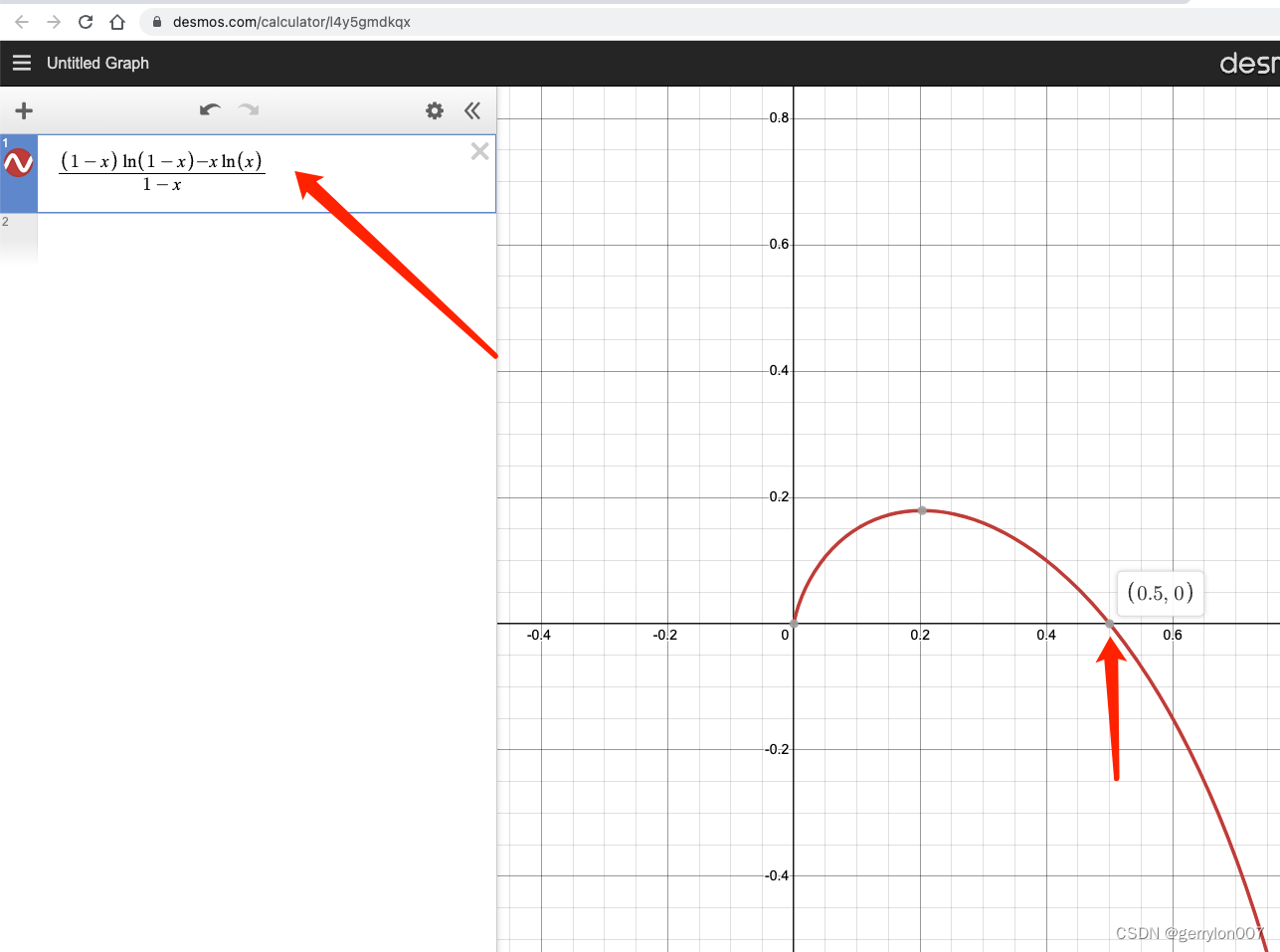
BloomFilter原理学习
文章目录BloomFilter简单介绍BloomFilter中的数学知识fpp(误判率/假阳性)的计算k的最小值公式总结编程语言实现golang的实现[已知n, p求m和k](https://github.com/bits-and-blooms/bloom/blob/master/bloom.go#L133)参考BloomFilter简单介绍 BloomFilter我们可能经常听到也在使…...

C语言老题新解第1-5题
文章目录1 互不相同且无重复数字2 企业利润提成3 两个完全平方数4 判断一年的第几天5 三个整数比较大小1 互不相同且无重复数字 1 有1, 2, 3, 4四个数字,能组成多少互不相同且无重复数字的三位数?都是多少? 最简单当然是三重循环嵌套在一起…...

【数据库系列】MQSQL历史数据分区
互联网行业企业都倾向于mysql数据库,虽说mysql单表能支持亿级别的数据量,加上索引优化下查询速度,勉强能使用,但是对于追求性能和效率的互联网企业,这是远远不够的。Mysql数据库单表数据量到达500万左右,达…...

MyBatis常用的俩种分页方式
1、使用 limit 实现分页 select * from xxx limit m,n # m 表示从第几条数据开始,默认从0开始 # n 表示查询几条数据 select * from xxx limit 2,3 # 从索引为2的数据开始,往后查询三个。2、3、4 (1) 创建分页对象,用来封装分页的数据 PS…...
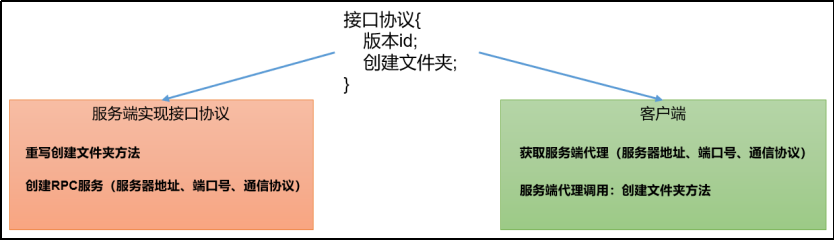
RPC通信原理解析
一、什么是RPC框架? RPC,全称为Remote Procedure Call,即远程过程调用,是一种计算机通信协议。 比如现在有两台机器:A机器和B机器,并且分别部署了应用A和应用B。假设此时位于A机器上的A应用想要调用位于B机…...

【蓝桥杯集训·周赛】AcWing 第93场周赛
文章目录第一题 AcWing 4867. 整除数一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解第二题 AcWing 4868. 数字替换一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解第三题 AcWing 4869. 异或值一、题目1、原题…...
蓝桥杯-刷题统计
蓝桥杯-刷题统计1、问题描述2、解题思路3、代码实现3.1 方案一:累加方法(超时)3.2 方案二1、问题描述 小明决定从下周一开始努力刷题准备蓝桥杯竞赛。他计划周一至周五每天做 a 道题目, 周六和周日每天做 b 道题目。请你帮小明计算, 按照计划他将在 第几天实现做题数…...

Linux入门教程||Linux Shell 变量|| Shell 传递参数
Shell 变量 定义变量时,变量名不加美元符号($,PHP语言中变量需要),如: your_name"w3cschool.cn"注意,变量名和等号之间不能有空格,这可能和你熟悉的所有编程语言都不一…...
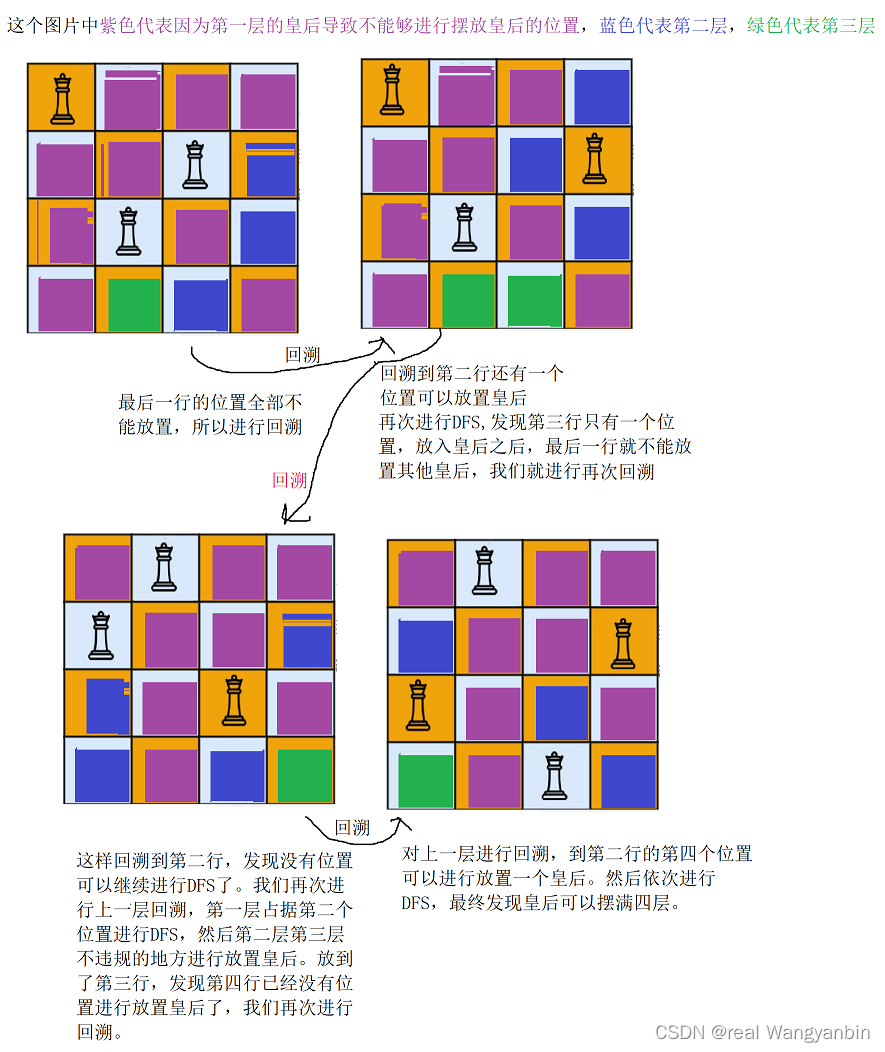
[算法和数据结构]--回溯算法之DFS初识
回溯算法——DFSDFS介绍(Depth First Search)DFS经典题目1. 员工的重要性2. 图像渲染3.被围绕的区域4.岛屿数量5. 电话号码的字母组合6.数字组合7. 活字印刷8. N皇后DFS介绍(Depth First Search) 回溯法(back tracking)(探索与回溯法&#x…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...
