BloomFilter原理学习
文章目录
- BloomFilter简单介绍
- BloomFilter中的数学知识
- fpp(误判率/假阳性)的计算
- k的最小值
- 公式总结
- 编程语言实现
- golang的实现
- [已知n, p求m和k](https://github.com/bits-and-blooms/bloom/blob/master/bloom.go#L133)
- 参考
BloomFilter简单介绍
BloomFilter我们可能经常听到也在使用, 它的特点是如果判断结果为"不存在", 则一定不存在; 如果判断为存在, 则可能存在. 如下图示例说明当我们判断z元素存在时, 其实是不存在的, 即存在有概率性.
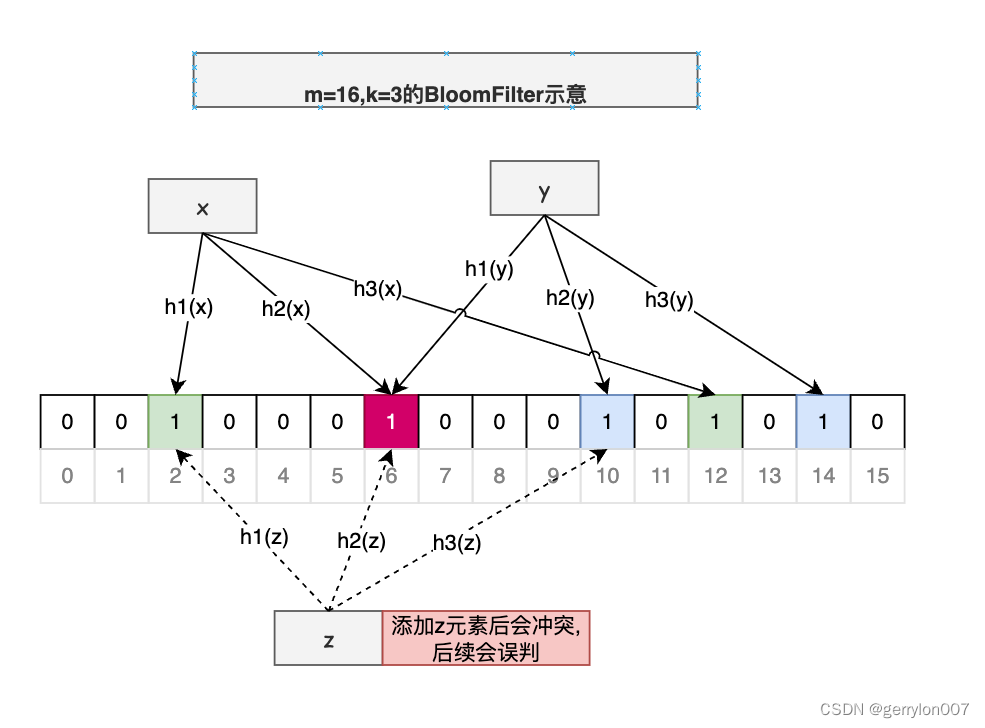
如上图, 长为m=16的二进制向量, 初始全为0; k=3(即添加一个元素需要将3个bit设置为1), 对n=3个元素进行添加操作.
BloomFilter几个关键量定义:
m: 二进制向量大小(多少个二进制位)
n: 要存放的元素个数
k: 哈希函数的个数, 或者说每添加一个元素都要进行k次计算
fpp或者简写为p: 误判率(false positive rate), 即 使用bloomfilter判断为存在时, 但实际不存在的概率
BloomFilter中的数学知识
fpp(误判率/假阳性)的计算
BloomFilter主要的数学原理是: 在某一范围内(1<=x<=m)1<=x<=m)1<=x<=m)(x为整数, m通常是很大的, 如106级别10^6级别106级别), 任意选取两个整数i,j,i和j可重复选取i, j, i和j可重复选取i,j,i和j可重复选取, 则其相等的概率是非常小的: mm2=1m\dfrac{m}{m^2}=\dfrac{1}{m}m2m=m1
我们假定hash计算是均匀的, 即每次hash会随机地将m位中的一位设置为1. 那么:
- 一次hash计算(如h1(x)h1(x)h1(x))后, 任一位被 置为1 的概率为: 1m\dfrac{1}{m}m1
- 一次hash计算(如h1(x)h1(x)h1(x))后, 任一位 还是0(即未被置为1) 的概率为: 1−1m1 - \dfrac{1}{m}1−m1
- 添加一个元素(如
bloomFilter.Add(x), 即执行k次hash)后, 任一位还是0的概率为: (1−1m)k(1 - \dfrac{1}{m})^k(1−m1)k - 添加n个元素后(如上图中的n=3个元素:x,y,z), 任一位还是0的概率为: (1−1m)kn(1 - \dfrac{1}{m})^{kn}(1−m1)kn , 任一位为1的概率为 1−(1−1m)kn1- (1 - \dfrac{1}{m})^{kn}1−(1−m1)kn
- 如果将1个新的元素,添加到已存在n个元素的BloomFilter中,则任一位已经为1的概率与上面相同,为:1−(1−1m)kn1- (1 - \dfrac{1}{m})^{kn}1−(1−m1)kn .
那么添加这个新元素时, k个比特都为1(相当于新元素和已有元素已经分不清了)的概率(此即为新插入元素的误识别率)为:
p=[1−(1−1m)kn]kp = [1- (1 - \dfrac{1}{m})^{kn}]^{k} p=[1−(1−m1)kn]k
通常来说, m是一个非常大的数(1MiB内存就有220×8≈800万2^{20}\times{8}\approx 800万220×8≈800万个bit), 并且我们有: limx→∞(1+x)1x=e{ \lim\limits_{x \to \infin} (1+x)^{\frac{1}{x}} = e}x→∞lim(1+x)x1=e
那么在工程实践中, 可以认为p的近似值为:
p=[1−(1−1m)kn]k=[1−(1−1m)−m×−knm]k≈(1−e−knm)k(当m很大时,将−1m看作x)\begin{aligned} p &= [1- (1 - \dfrac{1}{m})^{kn}]^{k} \\ &= [1- (1 - \dfrac{1}{m})^{-m\times\frac{-kn}{m}}]^{k} \\ &\approx (1-e^{-\frac{kn}{m}})^{k} \enspace (当m很大时, 将 -\dfrac{1}{m}看 作x) \end{aligned} p=[1−(1−m1)kn]k=[1−(1−m1)−m×m−kn]k≈(1−e−mkn)k(当m很大时,将−m1看作x)
k的最小值
计算过程参考: https://cs.stackexchange.com/questions/132088/how-is-the-optimal-number-of-hashes-is-derived-in-bloom-filter
已经遗忘的知识:
- 求导公式: (lnx)′=1x(\ln{x})^{'} = \dfrac{1}{x}(lnx)′=x1
- 求导公式: (enx)′=nenx(\bold{e}^{nx})^{'} = n\bold{e}^{nx}(enx)′=nenx
在某些情况下, 我们对n, m, 的值可以给一个估算值, 以此来获得最小的p(即尽可能准确判断), 那么k就是一个变量了, 问题就变为求 (1−e−knm)k(1-e^{-\frac{kn}{m}})^{k}(1−e−mkn)k的最小值.
令f(k)=(1−e−knm)kf(k)=(1-e^{-\frac{kn}{m}})^{k}f(k)=(1−e−mkn)k, 那么
两边取对数有:lnf(k)=ln(1−e−knm)k=kln(1−e−knm)设g(k)=kln(1−e−knm),那么:g′(k)=ln(1−e−knm)+knme−knm1−e−knm令x=e−knm,x∈(0,1),那么有h(x)=ln(1−x)−x1−xlnx(注意k用−mnlnx替换)=(1−x)ln(1−x)−xlnx1−x(x∈0,1)\begin{aligned} & 两边取对数有: \\ & \ln f(k)=\ln (1-e^{-\frac{kn}{m}})^{k} = k \ln(1-e^{-\frac{kn}{m}}) \\ & 设 g(k) = k\ln{(1-e^{-\frac{kn}{m}})}, 那么:\\ & g{'}(k) = \ln{(1-e^{-\frac{kn}{m}})} + k\dfrac{\frac{n}{m}e^{-\frac{kn}{m}}}{1-e^{-\frac{kn}{m}}} \enspace \\ & 令 x = e^{-\frac{kn}{m}}, x \in(0, 1), 那么有 \\ & h(x) = \ln(1-x) - \dfrac{x}{1-x} \ln x \enspace (注意k用-\dfrac{m}{n}lnx替换) \\ & \enspace \enspace \enspace \enspace = \dfrac{(1-x) \ln(1-x)-x \ln x}{1-x} \enspace (x\in{0, 1}) \end{aligned} 两边取对数有:lnf(k)=ln(1−e−mkn)k=kln(1−e−mkn)设g(k)=kln(1−e−mkn),那么:g′(k)=ln(1−e−mkn)+k1−e−mknmne−mkn令x=e−mkn,x∈(0,1),那么有h(x)=ln(1−x)−1−xxlnx(注意k用−nmlnx替换)=1−x(1−x)ln(1−x)−xlnx(x∈0,1)
对 h(x)=(1−x)ln(1−x)−xlnx1−x(x∈0,1)h(x) = \dfrac{(1-x)\ln(1-x)-x \ln x}{1-x} \enspace (x\in{0, 1})h(x)=1−x(1−x)ln(1−x)−xlnx(x∈0,1), 不难看出:
- 当x=12时,h(x)=0x=\dfrac{1}{2}时, h(x)=0x=21时,h(x)=0
- 当x>12时,h(x)<0x>\dfrac{1}{2}时,h(x)<0x>21时,h(x)<0
- 当x<12时,h(x)>0x<\dfrac{1}{2}时,h(x)>0x<21时,h(x)>0
站在巨人的肩膀上, 我们可以直接在这里看:
显然在x∈(0,1)范围内,当x=0.5时,h(x)最小x\in(0, 1)范围内, 当x=0.5时, h(x)最小x∈(0,1)范围内,当x=0.5时,h(x)最小, 此时k=mnln2k=\dfrac{m}{n}ln2k=nmln2
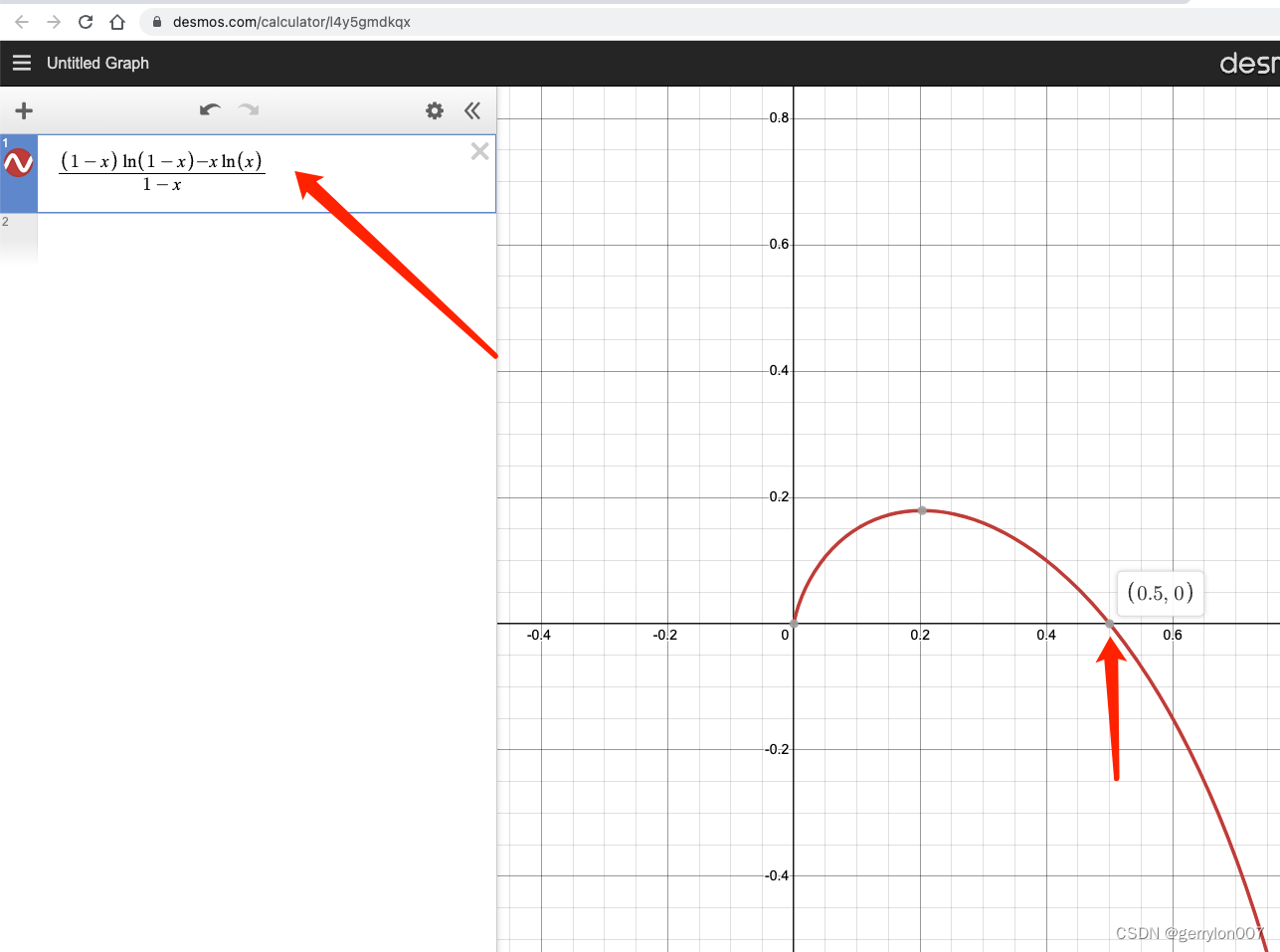
也就是说:
当k<mnln2k <\dfrac{m}{n}ln2k<nmln2时(想象k非常接近0), x=e−knmx = e^{-\frac{kn}{m}}x=e−mkn会非常接近1, 此时x>12x>\dfrac{1}{2}x>21,
h(x)<0h(x)<0h(x)<0 ⇒ f(k)在变小;
当k>mnln2k >\dfrac{m}{n}ln2k>nmln2时(想象k非常接近0), x=e−knmx = e^{-\frac{kn}{m}}x=e−mkn会非常接近0, 此时x<12x<\dfrac{1}{2}x<21,
h(x)>0h(x)>0h(x)>0 ⇒ f(k)在变大;
所以k=mnln2k=\dfrac{m}{n}ln2k=nmln2时会使得f(k)f(k)f(k)最小, 即此时p最小.
公式总结
- 误判率公式: p=[1−(1−1m)kn]kp = [1- (1 - \dfrac{1}{m})^{kn}]^{k}p=[1−(1−m1)kn]k
- 误判率近似公式(当
m很大时): p≈(1−e−knm)kp \approx (1-e^{-\frac{kn}{m}})^{k}p≈(1−e−mkn)k - 已知
m,n, k的最小值(近似)为: k=mnln2≈0.7mnk=\dfrac{m}{n}\ln{2} \approx 0.7\dfrac{m}{n}k=nmln2≈0.7nm - 已知
n,p, 且k取最小时, m=−nlnp(ln2)2m=-\dfrac{n\ln{p}}{(ln2)^{2}}m=−(ln2)2nlnp
编程语言实现
golang的实现
https://github.com/bits-and-blooms/bloom
已知n, p求m和k
func EstimateParameters(n uint, p float64) (m uint, k uint) {m = uint(math.Ceil(-1 * float64(n) * math.Log(p) / math.Pow(math.Log(2), 2)))k = uint(math.Ceil(math.Log(2) * float64(m) / float64(n)))return
}
参考
- https://en.wikipedia.org/wiki/Bloom_filter
- https://cs.stackexchange.com/questions/132088/how-is-the-optimal-number-of-hashes-is-derived-in-bloom-filter
(完)
相关文章:

BloomFilter原理学习
文章目录BloomFilter简单介绍BloomFilter中的数学知识fpp(误判率/假阳性)的计算k的最小值公式总结编程语言实现golang的实现[已知n, p求m和k](https://github.com/bits-and-blooms/bloom/blob/master/bloom.go#L133)参考BloomFilter简单介绍 BloomFilter我们可能经常听到也在使…...

C语言老题新解第1-5题
文章目录1 互不相同且无重复数字2 企业利润提成3 两个完全平方数4 判断一年的第几天5 三个整数比较大小1 互不相同且无重复数字 1 有1, 2, 3, 4四个数字,能组成多少互不相同且无重复数字的三位数?都是多少? 最简单当然是三重循环嵌套在一起…...

【数据库系列】MQSQL历史数据分区
互联网行业企业都倾向于mysql数据库,虽说mysql单表能支持亿级别的数据量,加上索引优化下查询速度,勉强能使用,但是对于追求性能和效率的互联网企业,这是远远不够的。Mysql数据库单表数据量到达500万左右,达…...

MyBatis常用的俩种分页方式
1、使用 limit 实现分页 select * from xxx limit m,n # m 表示从第几条数据开始,默认从0开始 # n 表示查询几条数据 select * from xxx limit 2,3 # 从索引为2的数据开始,往后查询三个。2、3、4 (1) 创建分页对象,用来封装分页的数据 PS…...
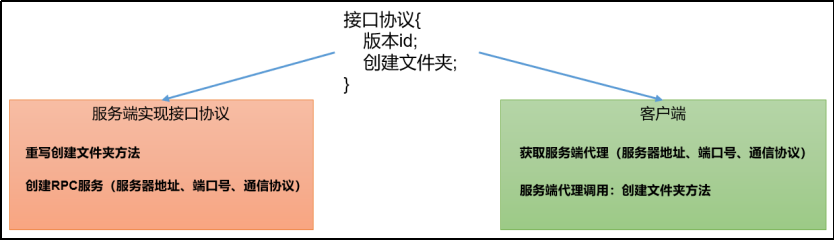
RPC通信原理解析
一、什么是RPC框架? RPC,全称为Remote Procedure Call,即远程过程调用,是一种计算机通信协议。 比如现在有两台机器:A机器和B机器,并且分别部署了应用A和应用B。假设此时位于A机器上的A应用想要调用位于B机…...

【蓝桥杯集训·周赛】AcWing 第93场周赛
文章目录第一题 AcWing 4867. 整除数一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解第二题 AcWing 4868. 数字替换一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解第三题 AcWing 4869. 异或值一、题目1、原题…...
蓝桥杯-刷题统计
蓝桥杯-刷题统计1、问题描述2、解题思路3、代码实现3.1 方案一:累加方法(超时)3.2 方案二1、问题描述 小明决定从下周一开始努力刷题准备蓝桥杯竞赛。他计划周一至周五每天做 a 道题目, 周六和周日每天做 b 道题目。请你帮小明计算, 按照计划他将在 第几天实现做题数…...

Linux入门教程||Linux Shell 变量|| Shell 传递参数
Shell 变量 定义变量时,变量名不加美元符号($,PHP语言中变量需要),如: your_name"w3cschool.cn"注意,变量名和等号之间不能有空格,这可能和你熟悉的所有编程语言都不一…...
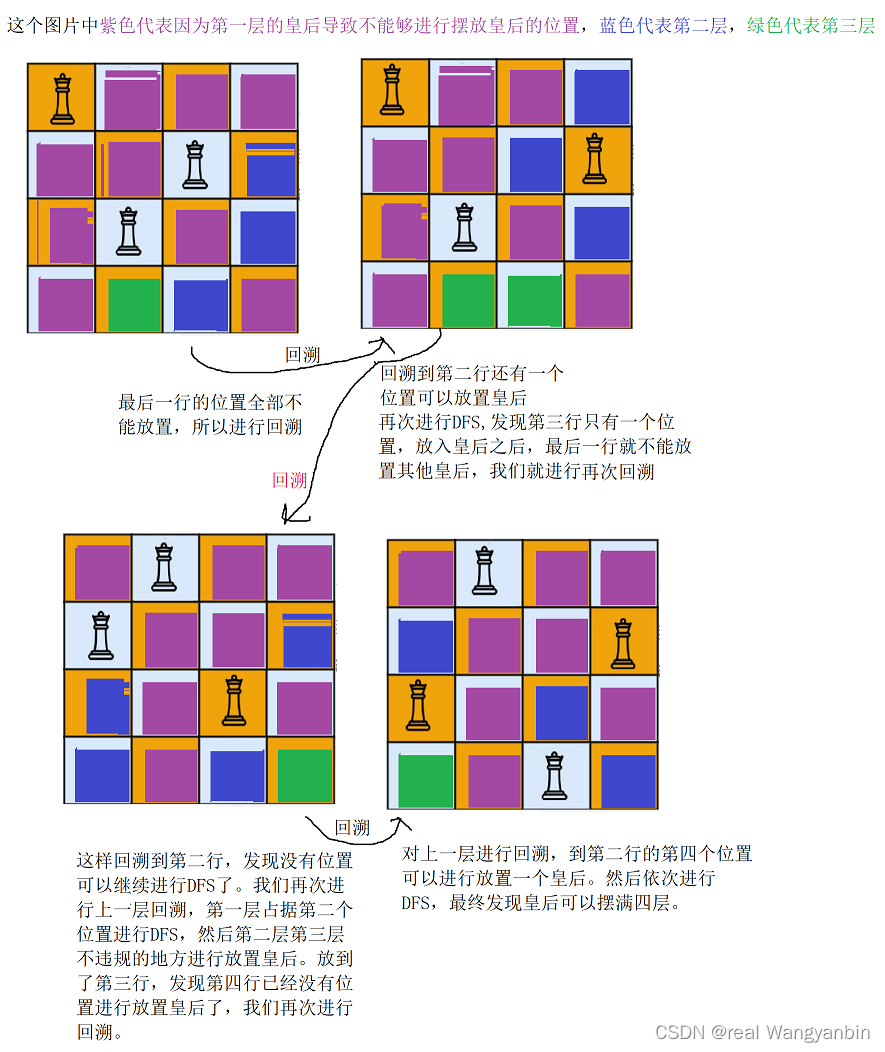
[算法和数据结构]--回溯算法之DFS初识
回溯算法——DFSDFS介绍(Depth First Search)DFS经典题目1. 员工的重要性2. 图像渲染3.被围绕的区域4.岛屿数量5. 电话号码的字母组合6.数字组合7. 活字印刷8. N皇后DFS介绍(Depth First Search) 回溯法(back tracking)(探索与回溯法&#x…...
【LeetCode每日一题】——680.验证回文串 II
文章目录一【题目类别】二【题目难度】三【题目编号】四【题目描述】五【题目示例】六【解题思路】七【题目提示】八【时间频度】九【代码实现】十【提交结果】一【题目类别】 贪心算法 二【题目难度】 简单 三【题目编号】 680.验证回文串 II 四【题目描述】 给你一个字…...

【C语言进阶:指针的进阶】你真分得清sizeof和strlen?
本章重点内容: 字符指针指针数组数组指针数组传参和指针传参函数指针函数指针数组指向函数指针数组的指针回调函数指针和数组面试题的解析这篇博客 FLASH 将带大家一起来练习一些容易让人凌乱的题目,通过这些题目来进一步加深和巩固对数组,指…...
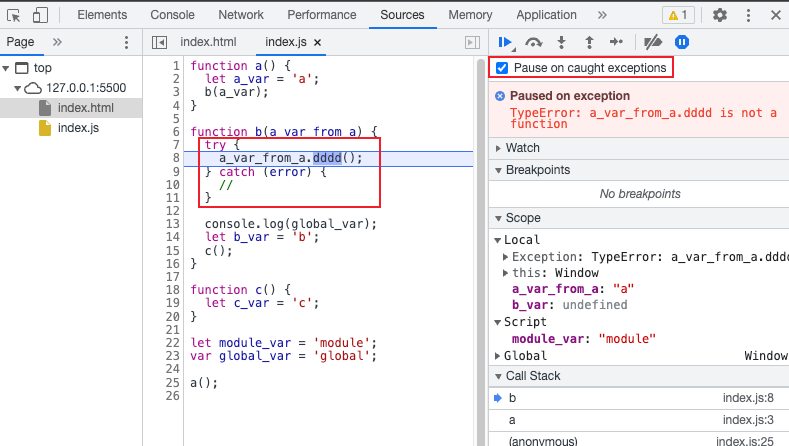
【前端必看】极大提高开发效率的网页 JS 调试技巧
大家好,我是前端西瓜哥。本文讲解如何使用浏览器提供的工具进行 JS 代码的断点调试。 debugger 在代码中需要打断点的地方,加上 debugger,表示一个断点。浏览器代码执行到该位置时,会停下来,进入调试模式。 示例代码…...

【春招面经】视源股份前端一面
前言 本次主要记录一下视源股份CVTE前端一面 (3.3下午4点15) 文章目录前言本次主要记录一下视源股份CVTE前端一面 (3.3下午4点15)问题总结介绍一下项目的来源以及做这个项目的初衷一直监听滚动,有没有对性能产生影响&a…...
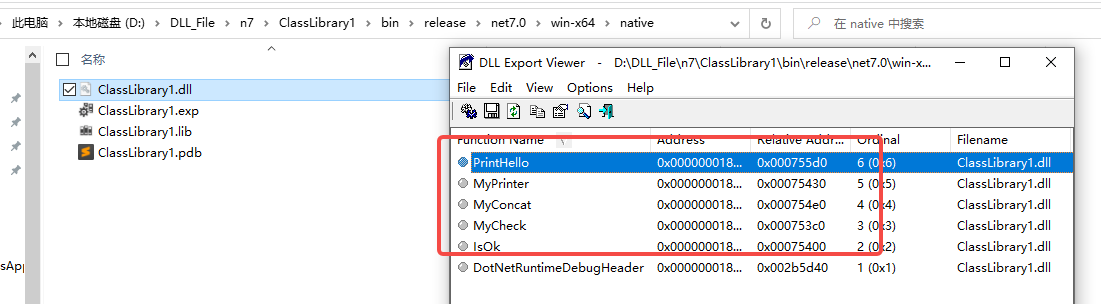
插件化开发入门
一、背景顾名思义,插件化开发就是将某个功能代码封装为一个插件模块,通过插件中心的配置来下载、激活、禁用、或者卸载,主程序无需再次重启即可获取新的功能,从而实现快速集成。当然,实现这样的效果,必须遵…...

tftp、nfs 服务器环境搭建
目录 一、认识 tftp、nfs 1、什么是 tftp? 2、什么是 nfs? 3、tftp 和 nfs 的区别 二、tftp的安装 1、安装 tftp 服务端 2、配置 tftp 3、启动 tftp 服务 三、nfs 的安装 1、安装 nfs 服务端 2、配置 nfs 3、启动 nfs 服务 一、认识 tftp、…...
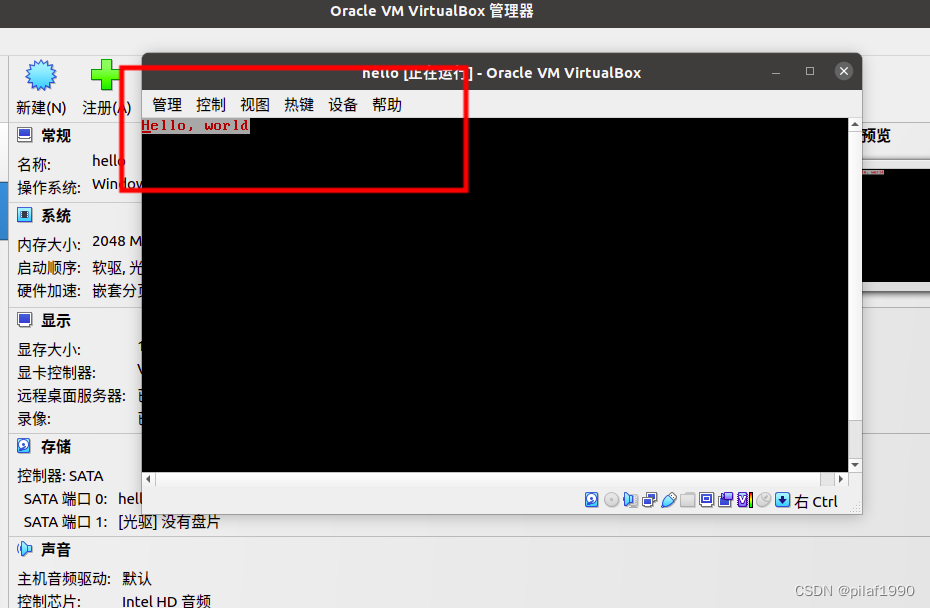
汇编系列03-不借助操作系统输出Hello World
每天进步一点点,加油! 上一节,我们通过汇编指令,借助操作系统的系统调用实现了向标准输出打印Hello world。这一节我们打算绕过操作系统,直接在显示屏幕上打印Hello world。 计算机的启动过程 当我们给计算机加电启…...

TPU编程竞赛系列|算能赛道冠军SO-FAST团队获第十届CCF BDCI总决赛特等奖!
近日,第十届中国计算机学会(CCF)大数据与计算智能大赛总决赛暨颁奖典礼在苏州顺利落幕,算能赛道的冠军队伍SO-FAST从2万余支队伍中脱颖而出,获得了所有赛道综合评比特等奖! 本届CCF大赛吸引了来自全国的2万…...
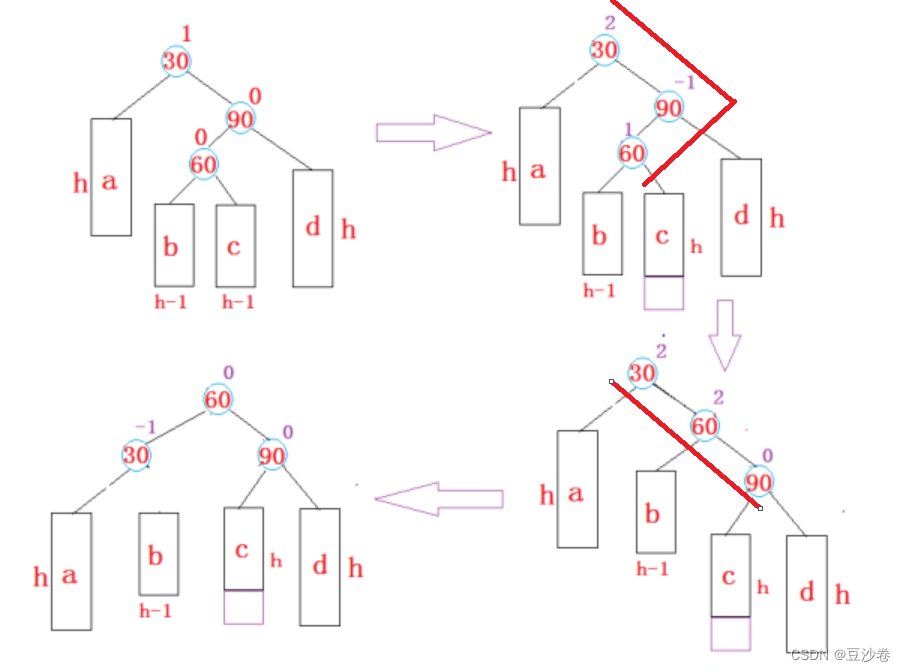
【C++】AVL树,平衡二叉树详细解析
文章目录前言1.AVL树的概念2.AVL树节点的定义3.AVL树的插入4.AVL树的旋转左单旋右单旋左右双旋右左双旋AVL树的验证AVL树的删除AVL树的性能前言 前面对map/multimap/set/multiset进行了简单的介绍,在其文档介绍中发现,这几个容器有个共同点是࿱…...
C/C++开发,无可避免的多线程(篇四).线程与函数的奇妙碰撞
一、函数、函数指针及函数对象 1.1 函数 函数(function)是把一个语句序列(函数体, function body)关联到一个名字和零或更多个函数形参(function parameter)的列表的 C 实体,可以通过返回或者抛…...

elisp简单实例: taglist
从vim 转到emacs 下,一直为缺少vim 中的tablist 插件而感到失落. 从网上得到的一个emacs中的taglist, 它的功能很简陋,而且没有任何说明, 把它做为elisp的简单实例,供初学者入门倒不错,我给它加了很多注释,帮助理解, 说实话,感觉这百行代码还是挺有深度的,慢慢体会,调试才会有收…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...
