2023thupc总结
A 大富翁
很有意思的题
∑x∈A∑y∈B[x支配y]−∑x∈A∑y∈B[y支配x]−∑x∈Awx\sum_{x\in A}\sum_{y\in B}[x支配y]-\sum_{x\in A}\sum_{y\in B}[y支配x]-\sum_{x\in A}w_x∑x∈A∑y∈B[x支配y]−∑x∈A∑y∈B[y支配x]−∑x∈Awx
=∑x∈A∑y[x支配y]−∑x∈A∑y[y支配x]−∑x∈Awx=\sum_{x\in A}\sum_{y}[x支配y]-\sum_{x\in A}\sum_{y}[y支配x]-\sum_{x\in A}w_x=∑x∈A∑y[x支配y]−∑x∈A∑y[y支配x]−∑x∈Awx
=∑x∈Asizx−∑x∈Adepx−∑x∈Awx=\sum_{x\in A}siz_x-\sum_{x\in A}dep_x-\sum_{x\in A}w_x=∑x∈Asizx−∑x∈Adepx−∑x∈Awx
这样每个点的贡献就确定了
排序后取奇数位
C 快速最小公倍数变换
考虑把贡献改写成一个只跟rir_iri相关,只跟rjr_jrj相关,只跟ri+rjr_i+r_jri+rj相关的三个数的乘积
设vp(x)v_p(x)vp(x)表示质数ppp在xxx质因数分解中的指数大小,MpM_pMp表示所有vp(ai)v_p(a_i)vp(ai)的最大值,mpm_pmp所有vp(ai)v_p(a_i)vp(ai)的非严格次大值
考虑算出MpM_pMp在操作之后的改变值ΔMp\Delta M_pΔMp
ΔMp=([vp(ri)=Mp]+[vp(rj)=Mp])(mp−Mp)+max(vp(ri+rj)−Mp,0)\Delta M_p=([v_p(r_i)=M_p]+[v_p(r_j)=M_p])(m_p-M_p)+\max(v_p(r_i+r_j)-M_p,0)ΔMp=([vp(ri)=Mp]+[vp(rj)=Mp])(mp−Mp)+max(vp(ri+rj)−Mp,0)
证明
当[vp(ri)=Mp]=0,[vp(rj)=Mp]=0[v_p(r_i)=M_p]=0,[v_p(r_j)=M_p]=0[vp(ri)=Mp]=0,[vp(rj)=Mp]=0时,显然满足
当[vp(ri)=Mp]=1,[vp(rj)=Mp]=0[v_p(r_i)=M_p]=1,[v_p(r_j)=M_p]=0[vp(ri)=Mp]=1,[vp(rj)=Mp]=0时,vp(ri+rj)=vp(rj)<Mpv_p(r_i+r_j)=v_p(r_j)<M_pvp(ri+rj)=vp(rj)<Mp,满足
当[vp(ri)=Mp]=0,[vp(rj)=Mp]=1[v_p(r_i)=M_p]=0,[v_p(r_j)=M_p]=1[vp(ri)=Mp]=0,[vp(rj)=Mp]=1时,与上种情况类似
当[vp(ri)=Mp]=1,[vp(rj)=Mp]=1[v_p(r_i)=M_p]=1,[v_p(r_j)=M_p]=1[vp(ri)=Mp]=1,[vp(rj)=Mp]=1时,mp=Mpm_p=M_pmp=Mp,满足
然后就能用nttnttntt优化了
相关文章:

2023thupc总结
A 大富翁 很有意思的题 ∑x∈A∑y∈B[x支配y]−∑x∈A∑y∈B[y支配x]−∑x∈Awx\sum_{x\in A}\sum_{y\in B}[x支配y]-\sum_{x\in A}\sum_{y\in B}[y支配x]-\sum_{x\in A}w_x∑x∈A∑y∈B[x支配y]−∑x∈A∑y∈B[y支配x]−∑x∈Awx ∑x∈A∑y[x支配y]−∑x∈A∑y[y支…...
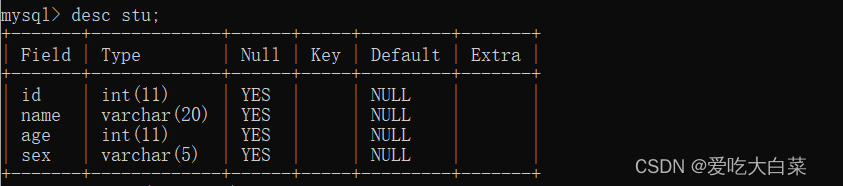
【数据库】MySQL数据库基础
目录 1.数据库: 2.数据库基本操作 2.1 MySQL的运行原理 2.2显示数据库: 2.3创建数据库 2.4使用数据库 2.5删除数据库 3.常见的数据类型 3.1数值类型: 3.2字符型类型 3.3日期类型 4.表的操作 4.1创建表 4.2查看表 4.3删除表 5.汇总…...
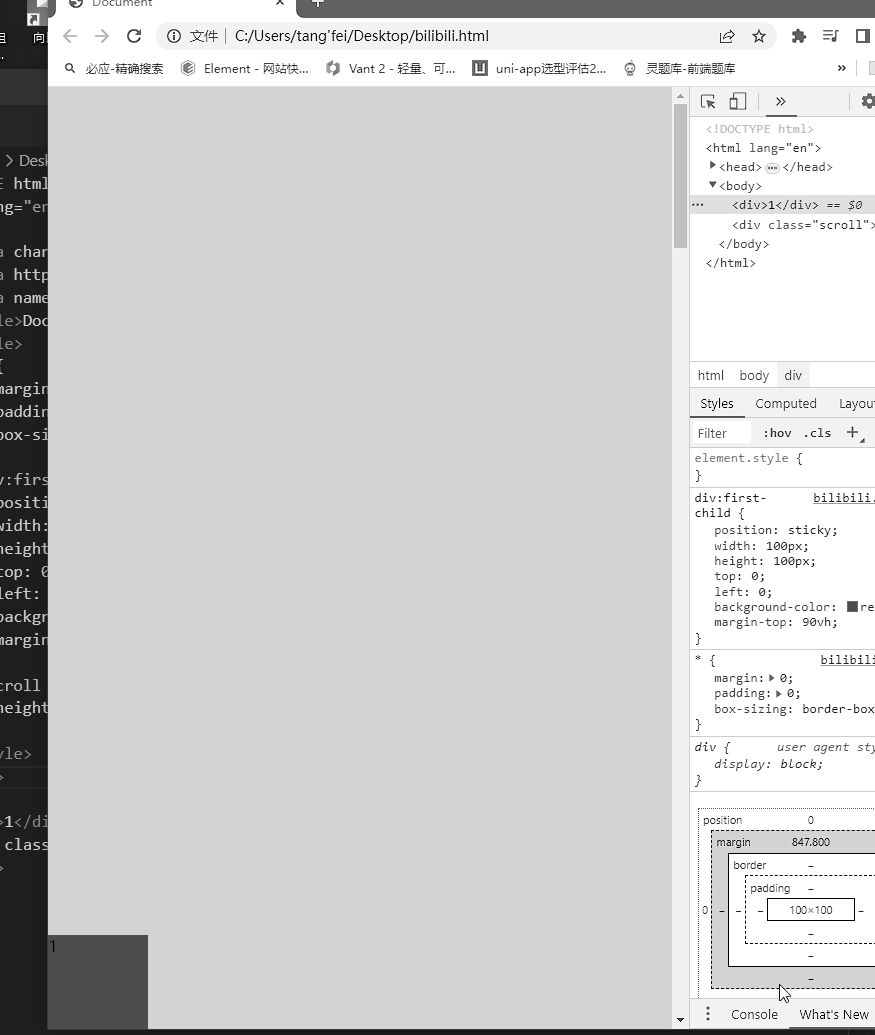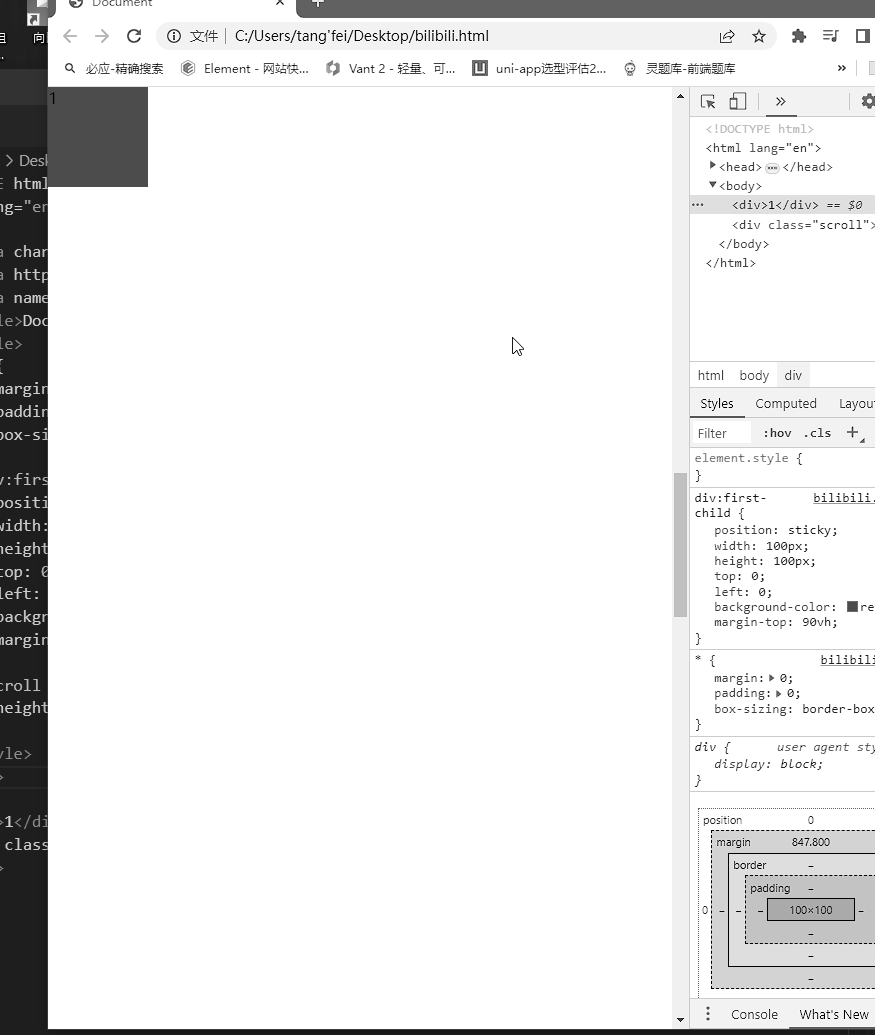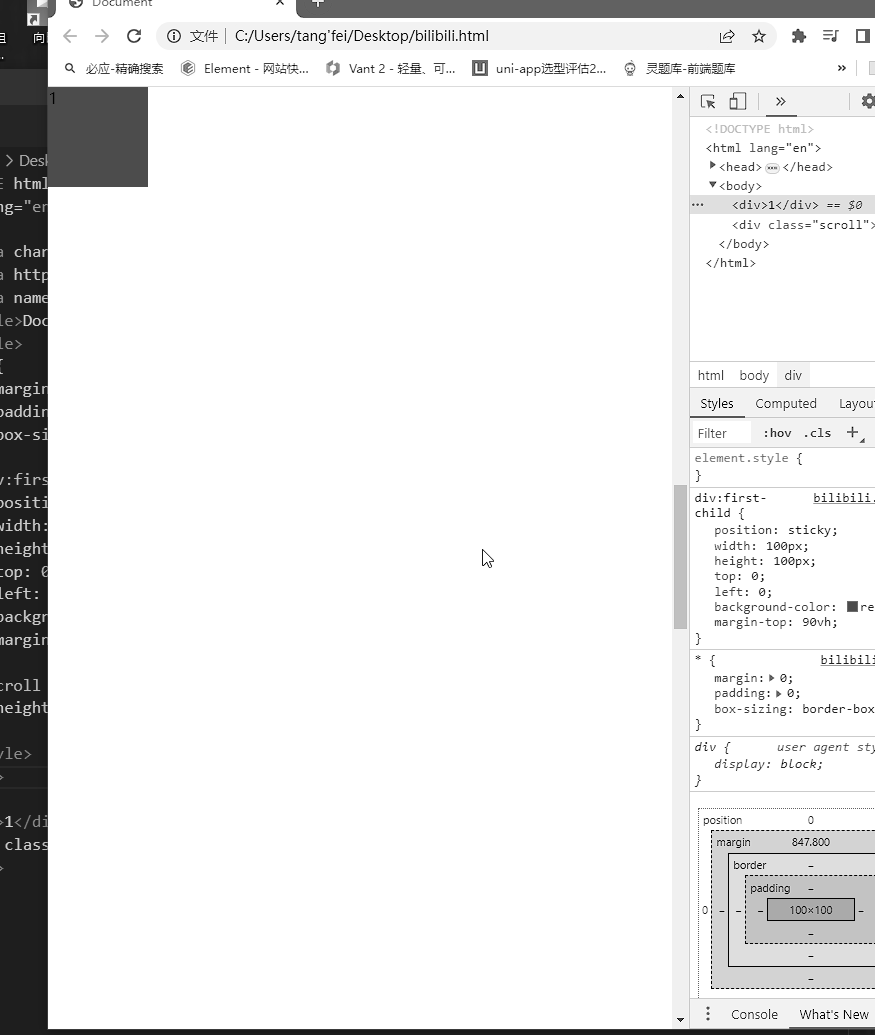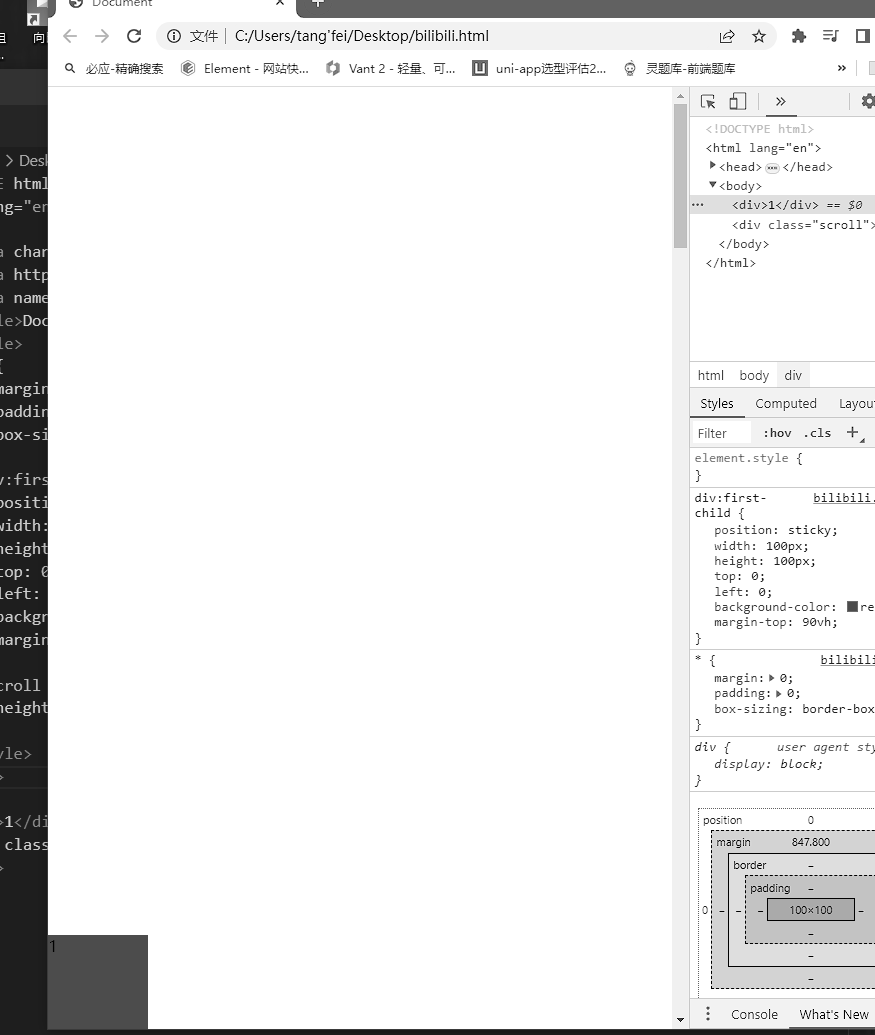
grid了解
结构 <div class"grid"><div>1</div><div>2</div><div>3</div><div>4</div><div>5</div><div>6</div><div>7</div><div>8</div><div>9</div>&l…...

2023年全国最新工会考试精选真题及答案13
百分百题库提供工会考试试题、工会考试预测题、工会考试真题、工会证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 81.女职工委员会在()下开展工作。 A.企业工会委员会领导 B.企业工会委员会指导 …...
初识HTML技术
文章目录一、为什么学习前端?二、第一个HTML文件VSCode三. HTML元素四. HTML页面一、为什么学习前端? 我们作为一个后端程序员,为什么还要学习前端,因为我们的终极目的是实现web开发,搭建网站,网站 前端 后端 比如我们随便…...

我们为什么要用消息队列?
消息队列是系统设计中存在时间最长的中间件之一,从系统有通信需求开始,就产生了消息队列。 消息队列的使用场景 在日常系统设计与实现的过程中,下面3种场景会涉及到消息队列: 异步处理流量控制服务解耦 异步处理 典型的应用场…...
Linux进程控制
进程控制fork函数进程终止退出码常见的退出方式进程等待什么是进程等待,为什么要进程等待阻塞与非阻塞进程替换替换原理替换函数执行系统命令执行自己写的程序模拟实现简易的shellfork函数 fork函数是创建一个子进程,之前用过。 #include <unistd.h…...
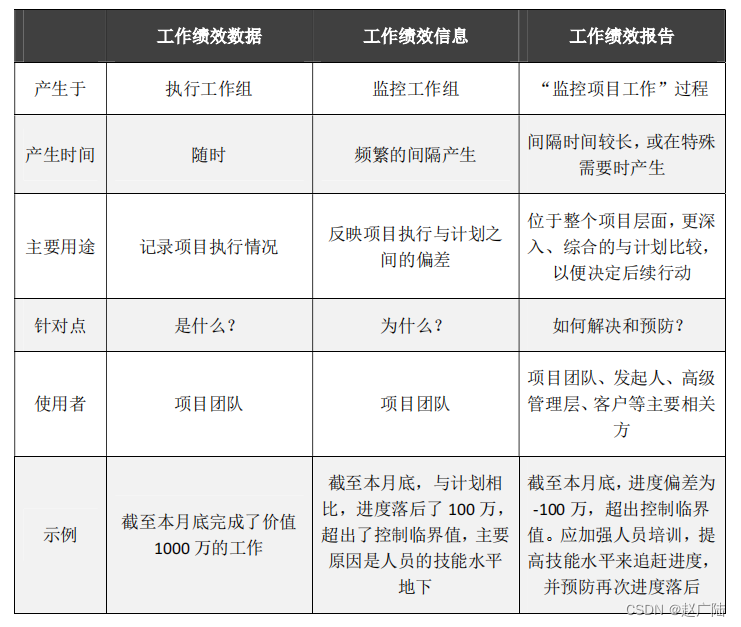
PMP项目管理引论介绍
目录1. 指南概述和目的1.1 项目管理标准1.2 道德与专业行为规范2 基本要素2.1 项目2.2 项目管理的重要性2.3 项目、项目集、项目组合以及运营管理之间的关系2.3.1 概述2.3.2. 项目组合与项目集管理2.3.3. 运营管理2.3.4. 组织级项目管理和战略2.3.5. 项目管理2.3.6. 运营管理与…...

计算机视觉废钢堆提取问题
计算机视觉废钢堆提取问题 背景介绍 在钢铁炼制中,废钢是非常重要的原料,不同等级废钢对于钢成品影响很大,因此需要对废钢进行正确分类。某废钢料场中,卸料区域布置了多个摄像头,用于拍摄卸料场中废钢堆,…...
)
判断水仙花数-课后程序(Python程序开发案例教程-黑马程序员编著-第二章-课后作业)
实例5:判断水仙花数 水仙花数是一个3位数,它的每位数字的3次幂之和等于它本身,例如13 53 33 153,153就是一个水仙花数。 本实例要求编写程序,实现判断用户输入的3位数是否为水仙花数的功能。 实例目标 掌握Pytho…...

目标检测: 数据增强代码详解
1. 常见的数据增强 1.1 翻转图像 左右水平翻转 假设图片的宽高为w,h,bdbox左上角A坐标为(x1,y1), 右下角B为(x2,y2)。经过左右水平翻转后,bdbox的左上角A1坐标(w-x2,y1) ,右下角B1坐标为(w-x1,y2)左右水平翻转的代码实现如下:from PIL import Image image = Image.open(i…...

第二讲:ambari编译复盘,如何实现一次性成功编译ambari
上节课我们已经讲解了如何成功编译ambari源码,安装ambari-server rpm包以及成功部署ambari。本节课我们来复盘一下上节课的编译过程,以及思考如何实现一次性成功编译ambari。 要想一次性成功编译ambari,那么就需要将预置工作做好,比如: maven镜像源配置,node_moudle模块…...

Windows下jdk安装与卸载-超详细的图文教程
jdk安装 下载jdk 由于现在主流就是jdk1.8,所以这里就下载jdk1.8进行演示。官方下载地址:https://www.oracle.com/java/technologies/downloads/#java8-windows。 官方下载需要注册oracle账号,国内下载有可能速度慢,若不想注册账…...

Jackson CVE-2018-5968 反序列化漏洞
0x00 前言 同CVE-2017-15095一样,是CVE-2017-7525黑名单绕过的漏洞,主要还是看一下绕过的调用链利用方式。 可以先看: Jackson 反序列化漏洞原理 或者直接看总结也可以: Jackson总结 影响版本:至2.8.11和2.9.x至…...
考试中一道大部分同学都会做错的题目)
解析MySQL 8.0 OCP(1Z0-908)考试中一道大部分同学都会做错的题目
一个用户有下面的权限: mysql>SHOW GRANTS FOR jsmith;---------------------------------------------------------------------- | Grants for jsmith% | ----------------------------------------------------------…...

Java死锁
什么是死锁? 多个线程同时被阻塞,它们中的一个或者全部都在等待某个资源被释放。由于线程被无限期地阻塞,因此程序不可能正常终止。 死锁的必要条件: 1、互斥条件:该资源任意一个时刻只由一个线程占用。 2、请求与…...
BloomFilter原理学习
文章目录BloomFilter简单介绍BloomFilter中的数学知识fpp(误判率/假阳性)的计算k的最小值公式总结编程语言实现golang的实现[已知n, p求m和k](https://github.com/bits-and-blooms/bloom/blob/master/bloom.go#L133)参考BloomFilter简单介绍 BloomFilter我们可能经常听到也在使…...

C语言老题新解第1-5题
文章目录1 互不相同且无重复数字2 企业利润提成3 两个完全平方数4 判断一年的第几天5 三个整数比较大小1 互不相同且无重复数字 1 有1, 2, 3, 4四个数字,能组成多少互不相同且无重复数字的三位数?都是多少? 最简单当然是三重循环嵌套在一起…...

【数据库系列】MQSQL历史数据分区
互联网行业企业都倾向于mysql数据库,虽说mysql单表能支持亿级别的数据量,加上索引优化下查询速度,勉强能使用,但是对于追求性能和效率的互联网企业,这是远远不够的。Mysql数据库单表数据量到达500万左右,达…...

MyBatis常用的俩种分页方式
1、使用 limit 实现分页 select * from xxx limit m,n # m 表示从第几条数据开始,默认从0开始 # n 表示查询几条数据 select * from xxx limit 2,3 # 从索引为2的数据开始,往后查询三个。2、3、4 (1) 创建分页对象,用来封装分页的数据 PS…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
