【数学基础】
文章目录
- 『 第1讲 高等数学预备知识 』
- 1.1 函数的概念与特性
- 函数的四种特性
- 【 重要结论 】
- 1.2 函数的图像
- 直角坐标系下的图像
- 极坐标系下的图像
- 参数方程
- 1.3 常用基础知识
- 【 情报#1 】
- 『 第2讲 数列极限 』
- 2.1 引言
- 2.2 求数列极限
- 【 情报#2 】
『 第1讲 高等数学预备知识 』
1.1 函数的概念与特性
- 函数
- 反函数:函数与反函数的图像、对称
- 复合函数
函数的四种特性
- 有界性:“完全包围”,指明区间,无界
- 单调性:定义法、求导法
- 奇偶性:特殊的奇偶函数,特点,悬链线
- 周期性
【 重要结论 】
- 七条重要结论(p4)
1.2 函数的图像
直角坐标系下的图像
- 常见图像
- 基本初等函数:常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数
- 常数函数:作用
- 幂函数:图像,定义域、值域,常用幂函数,单调性
- 指数函数:图像,定义域、值域,单调性,常用指数函数,极限,特殊函数值
- 对数函数:图像,定义域、值域,单调性,常用对数函数,极限,特殊函数值,常用公式(幂指函数)
- 三角函数:图像,定义域、值域,奇偶性,周期性,有界性,特殊函数值
- 正弦函数&余弦函数
- 正切函数&余切函数
- 反三角函数:图像,定义域、值域,单调性,奇偶性,有界性,性质
- 反正弦函数&反余弦函数
- 反正切函数&反余切函数
- 初等函数:幂指函数
- 分段函数:绝对值函数,符号函数,取整函数、两个注意点
- 基本初等函数:常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数
- 图像变换
- 平移变换:左右、上下
- 对称变换:x轴、y轴、原点、y=x、绝对值
- 伸缩变换:水平伸缩、垂直伸缩
极坐标系下的图像
- 描点法画常见图像
- 心形线
- 玫瑰线
- 阿基米德螺线
- 伯努利双纽线
- 直角坐标系观点画极坐标系下图像:画直角系下r,θ图像,对应到极坐标系下
参数方程
- 摆线:外摆、平摆、内摆
- 星形线
1.3 常用基础知识
- 数列
- 等差数列
- 等比数列
- 常见数列前n项和
- 【 三角函数 】
- 三角函数基本关系
- 诱导公式
- 特殊的三角函数值
- 重要公式:倍角公式、半角公式、和差公式、积化和差公式/和差化积公式、万能公式
- 指数运算法则
- 对数运算法则
- 一元二次方程基础
- 因式分解公式
- 阶乘与双阶乘
- 【 常用不等式 】
【 情报#1 】
- 神秘的数字0/1
- 相同单调性替换放缩,简化计算
『 第2讲 数列极限 』
2.1 引言
2.2 求数列极限
- 证明1/2:定义 / 性质
- 【 三部曲 / ε语言 】
- 数列极限定义:四要素
- 收敛数列性质:唯一性、有界性、保号性、推论
- 运算规则
- 证明3:【 夹逼准则 】
- 证明4:【 单调有界准则 】
【 情报#2 】
- 脱帽 / 带帽 公式
- 重点研究不等关系
- 十大不等式
- 无界变量但不是无穷大量
- 数列收敛,数列子列亦收敛,且极限值相同
- {An}发散 <= 至少一个子列收敛,或两个子列收敛 但收敛值不同
- 普遍规律:存在即唯一
- 思路:
- 证明An → 0,转化为| An | → 0
- 单调递推式 => 单调有界准则
- 证明1:①先写距离,另起<ε ②反解除n的范围:n>g(ε) ③取N=[ g(ε) ] + 1
相关文章:

【数学基础】
文章目录『 第1讲 高等数学预备知识 』1.1 函数的概念与特性函数的四种特性【 重要结论 】1.2 函数的图像直角坐标系下的图像极坐标系下的图像参数方程1.3 常用基础知识【 情报#1 】『 第2讲 数列极限 』2.1 引言2.2 求数列极限【 情报#2 】『 第1讲 高等数学预备知识 』 1.1 …...
网上电子商城的设计与实现
技术:Java、JSP等摘要:21 世纪以来,人类经济高速发展,人们的生活发生了日新月异的变化,特别是计算机的应用及普及到经济和社会生活的各个领域。在消费领域,网上购物已经成为大众所接受的一种新型的消费方式…...

2023thupc总结
A 大富翁 很有意思的题 ∑x∈A∑y∈B[x支配y]−∑x∈A∑y∈B[y支配x]−∑x∈Awx\sum_{x\in A}\sum_{y\in B}[x支配y]-\sum_{x\in A}\sum_{y\in B}[y支配x]-\sum_{x\in A}w_x∑x∈A∑y∈B[x支配y]−∑x∈A∑y∈B[y支配x]−∑x∈Awx ∑x∈A∑y[x支配y]−∑x∈A∑y[y支…...
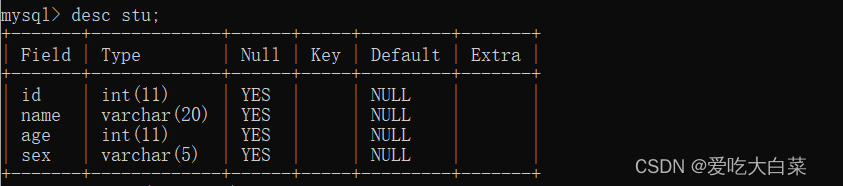
【数据库】MySQL数据库基础
目录 1.数据库: 2.数据库基本操作 2.1 MySQL的运行原理 2.2显示数据库: 2.3创建数据库 2.4使用数据库 2.5删除数据库 3.常见的数据类型 3.1数值类型: 3.2字符型类型 3.3日期类型 4.表的操作 4.1创建表 4.2查看表 4.3删除表 5.汇总…...
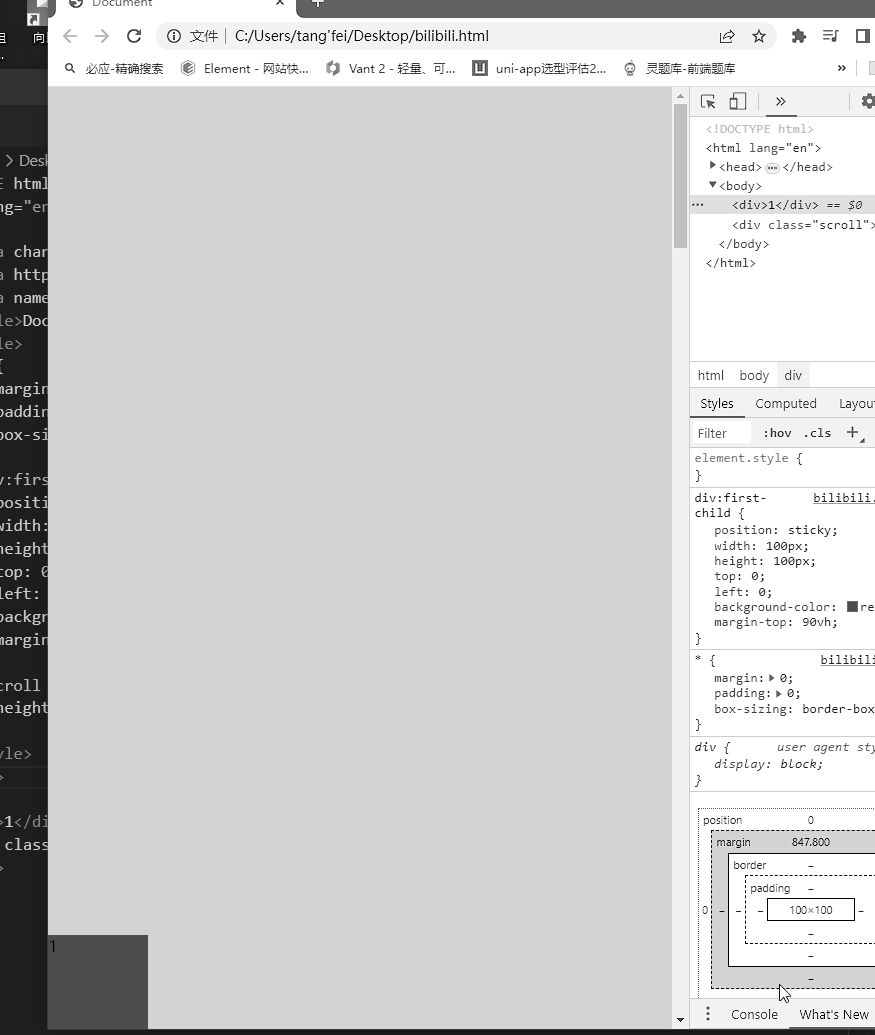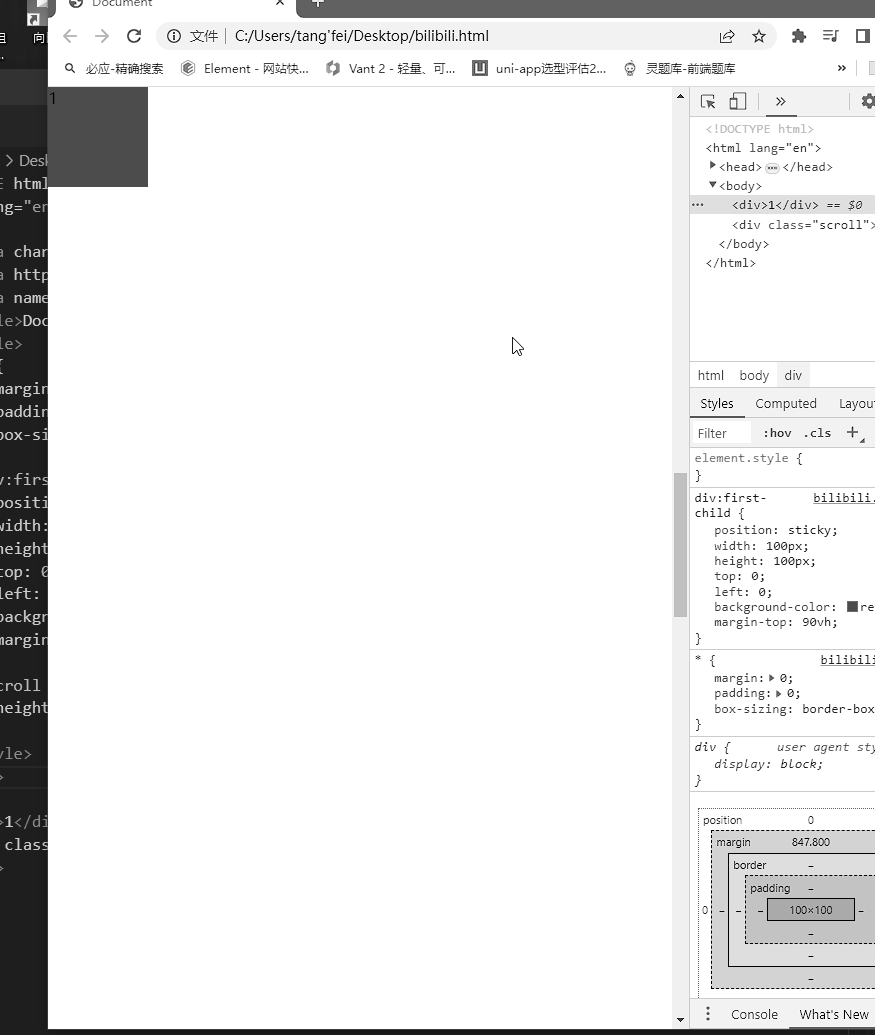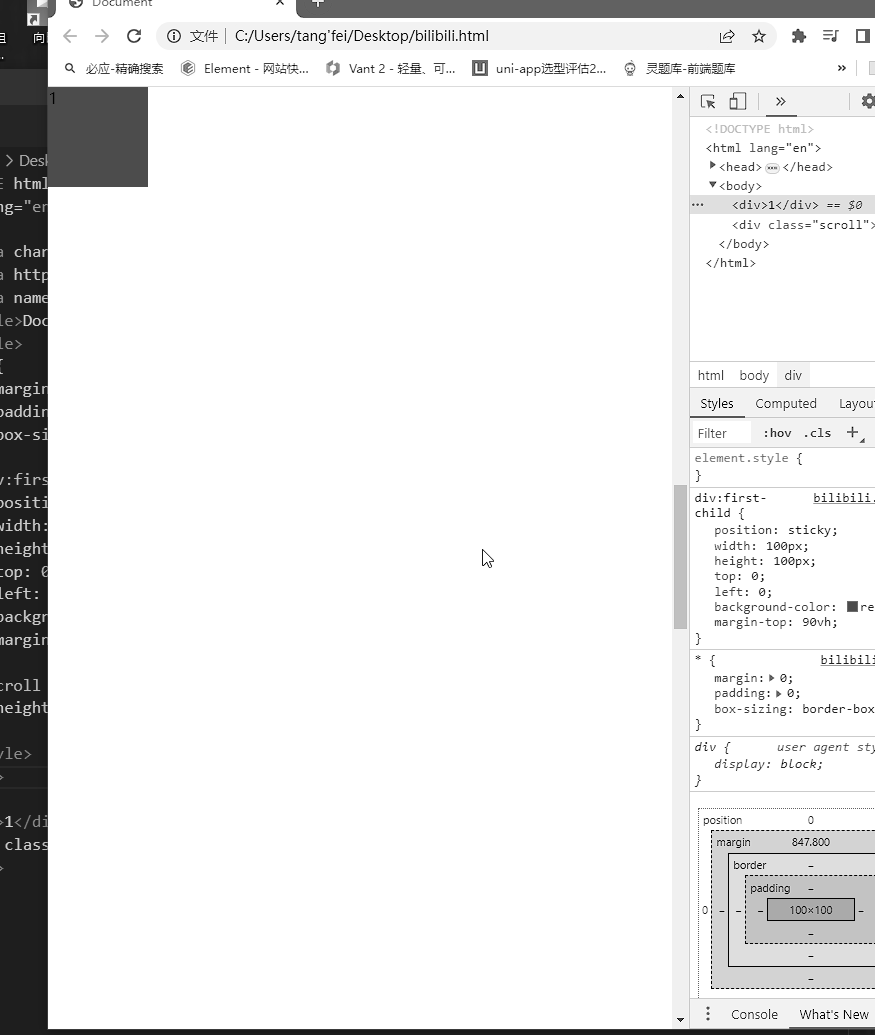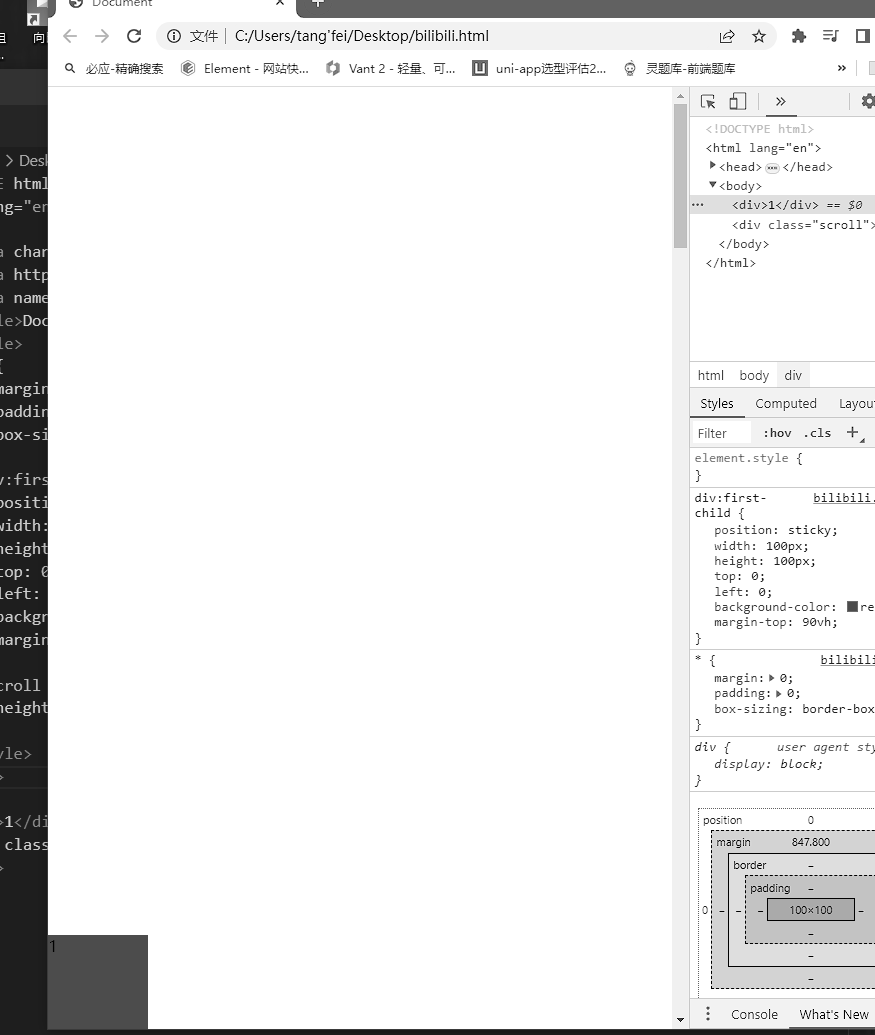
grid了解
结构 <div class"grid"><div>1</div><div>2</div><div>3</div><div>4</div><div>5</div><div>6</div><div>7</div><div>8</div><div>9</div>&l…...

2023年全国最新工会考试精选真题及答案13
百分百题库提供工会考试试题、工会考试预测题、工会考试真题、工会证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 81.女职工委员会在()下开展工作。 A.企业工会委员会领导 B.企业工会委员会指导 …...
初识HTML技术
文章目录一、为什么学习前端?二、第一个HTML文件VSCode三. HTML元素四. HTML页面一、为什么学习前端? 我们作为一个后端程序员,为什么还要学习前端,因为我们的终极目的是实现web开发,搭建网站,网站 前端 后端 比如我们随便…...

我们为什么要用消息队列?
消息队列是系统设计中存在时间最长的中间件之一,从系统有通信需求开始,就产生了消息队列。 消息队列的使用场景 在日常系统设计与实现的过程中,下面3种场景会涉及到消息队列: 异步处理流量控制服务解耦 异步处理 典型的应用场…...
Linux进程控制
进程控制fork函数进程终止退出码常见的退出方式进程等待什么是进程等待,为什么要进程等待阻塞与非阻塞进程替换替换原理替换函数执行系统命令执行自己写的程序模拟实现简易的shellfork函数 fork函数是创建一个子进程,之前用过。 #include <unistd.h…...
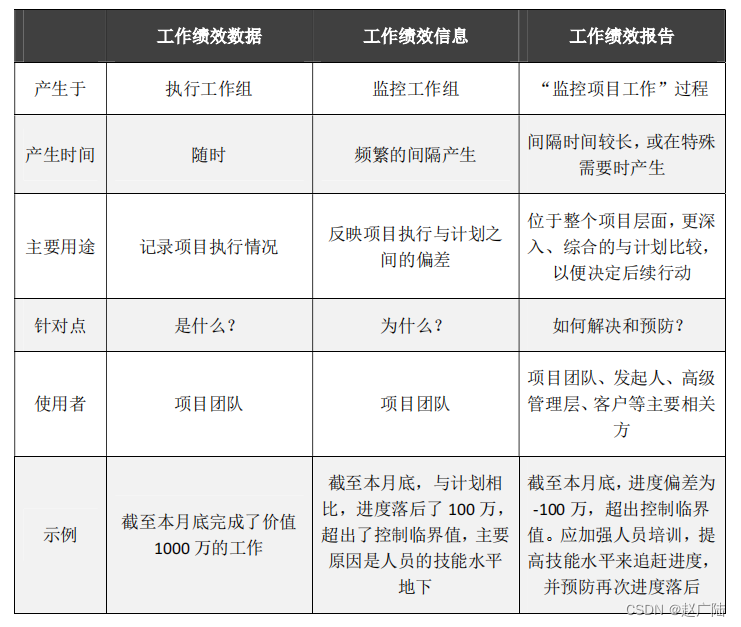
PMP项目管理引论介绍
目录1. 指南概述和目的1.1 项目管理标准1.2 道德与专业行为规范2 基本要素2.1 项目2.2 项目管理的重要性2.3 项目、项目集、项目组合以及运营管理之间的关系2.3.1 概述2.3.2. 项目组合与项目集管理2.3.3. 运营管理2.3.4. 组织级项目管理和战略2.3.5. 项目管理2.3.6. 运营管理与…...

计算机视觉废钢堆提取问题
计算机视觉废钢堆提取问题 背景介绍 在钢铁炼制中,废钢是非常重要的原料,不同等级废钢对于钢成品影响很大,因此需要对废钢进行正确分类。某废钢料场中,卸料区域布置了多个摄像头,用于拍摄卸料场中废钢堆,…...
)
判断水仙花数-课后程序(Python程序开发案例教程-黑马程序员编著-第二章-课后作业)
实例5:判断水仙花数 水仙花数是一个3位数,它的每位数字的3次幂之和等于它本身,例如13 53 33 153,153就是一个水仙花数。 本实例要求编写程序,实现判断用户输入的3位数是否为水仙花数的功能。 实例目标 掌握Pytho…...

目标检测: 数据增强代码详解
1. 常见的数据增强 1.1 翻转图像 左右水平翻转 假设图片的宽高为w,h,bdbox左上角A坐标为(x1,y1), 右下角B为(x2,y2)。经过左右水平翻转后,bdbox的左上角A1坐标(w-x2,y1) ,右下角B1坐标为(w-x1,y2)左右水平翻转的代码实现如下:from PIL import Image image = Image.open(i…...

第二讲:ambari编译复盘,如何实现一次性成功编译ambari
上节课我们已经讲解了如何成功编译ambari源码,安装ambari-server rpm包以及成功部署ambari。本节课我们来复盘一下上节课的编译过程,以及思考如何实现一次性成功编译ambari。 要想一次性成功编译ambari,那么就需要将预置工作做好,比如: maven镜像源配置,node_moudle模块…...

Windows下jdk安装与卸载-超详细的图文教程
jdk安装 下载jdk 由于现在主流就是jdk1.8,所以这里就下载jdk1.8进行演示。官方下载地址:https://www.oracle.com/java/technologies/downloads/#java8-windows。 官方下载需要注册oracle账号,国内下载有可能速度慢,若不想注册账…...

Jackson CVE-2018-5968 反序列化漏洞
0x00 前言 同CVE-2017-15095一样,是CVE-2017-7525黑名单绕过的漏洞,主要还是看一下绕过的调用链利用方式。 可以先看: Jackson 反序列化漏洞原理 或者直接看总结也可以: Jackson总结 影响版本:至2.8.11和2.9.x至…...
考试中一道大部分同学都会做错的题目)
解析MySQL 8.0 OCP(1Z0-908)考试中一道大部分同学都会做错的题目
一个用户有下面的权限: mysql>SHOW GRANTS FOR jsmith;---------------------------------------------------------------------- | Grants for jsmith% | ----------------------------------------------------------…...

Java死锁
什么是死锁? 多个线程同时被阻塞,它们中的一个或者全部都在等待某个资源被释放。由于线程被无限期地阻塞,因此程序不可能正常终止。 死锁的必要条件: 1、互斥条件:该资源任意一个时刻只由一个线程占用。 2、请求与…...
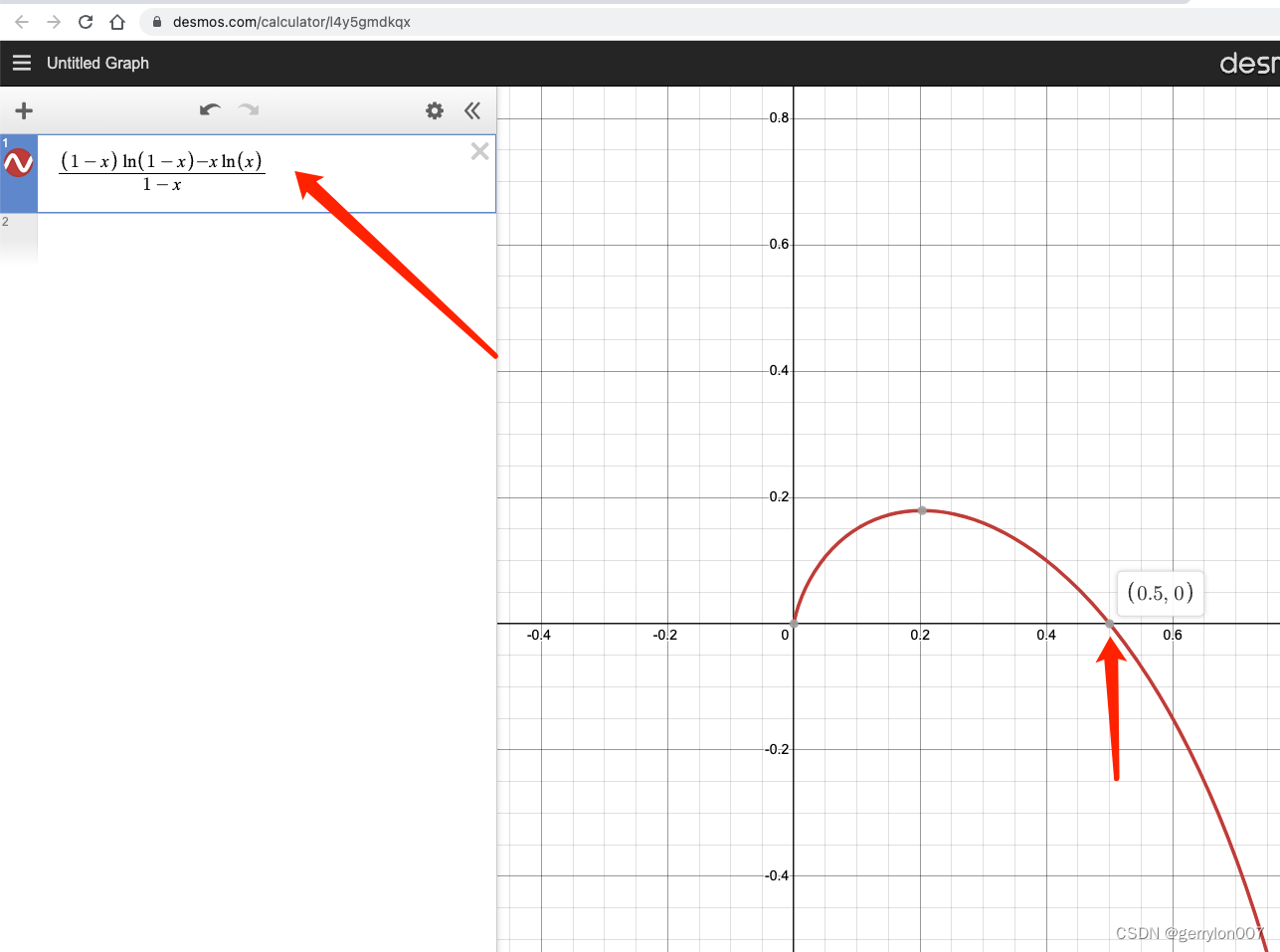
BloomFilter原理学习
文章目录BloomFilter简单介绍BloomFilter中的数学知识fpp(误判率/假阳性)的计算k的最小值公式总结编程语言实现golang的实现[已知n, p求m和k](https://github.com/bits-and-blooms/bloom/blob/master/bloom.go#L133)参考BloomFilter简单介绍 BloomFilter我们可能经常听到也在使…...

C语言老题新解第1-5题
文章目录1 互不相同且无重复数字2 企业利润提成3 两个完全平方数4 判断一年的第几天5 三个整数比较大小1 互不相同且无重复数字 1 有1, 2, 3, 4四个数字,能组成多少互不相同且无重复数字的三位数?都是多少? 最简单当然是三重循环嵌套在一起…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...
